弹道数据野值灰色自适应检测与修正∗
杨 军 张 东
(92941部队45分队 葫芦岛 125000)
1 引言
武器装备试验鉴定的过程就是一个获取和处理试验数据,并对装备的性能做出评定的、复杂的数据运动过程[1]。在数据测量过程中,由于弹上传感器测得的速度、位置、高度、加速度、压力等内弹道数据,以及由光电经纬仪、雷达等获得的外弹道数据,受复杂电磁环境、测控设备精度、人为操作过失等因素的综合影响或作用,获取的数据中不可避免地存在严重偏离被测数据真值的数据点,这些异常数据就称为野值[2]。野值可能导致处理结果严重失真,甚至完全失真[3]。因此,野值的检测与修正就成了数据处理工作的重要一环,它是提高数据处理精度、改善处理结果质量的有效措施。
目前,国内的专家和学者对野点剔除的方法作了大量研究[4~6],文献[4]结合工程实践,对已有的野值方法实验分析表明,差分法和多项式外推拟合法剔除孤立型野值点效果明显,但其门限的确定主要依赖于随机误差,同时容易将野点周围的合理数据拉偏。对于孤立型野值点,Kalman 滤波法和最小二乘B 样条逼近法剔除野值效果不明显,M-型估计-拉格朗日极值法剔除野值效果好,但对于野值的起始点和结束点的求解不够完善。文献[5]采用小波变换特征提取信息剔除数据中的野值,其算法效果显著,但计算量比较大。文献[6]提出一阶差分和外推拟合的联合野值剔除方法,能够找出斑点型野值在原始数据中的位置并加以剔除,但是需要对原始数据分段,增加了程序自动化实现难度。针对上述问题和算法上的不足,本文提出一种基于等维新息的弹道数据野值灰色自适应检测与修正方法,通过建立4 维灰色预测序列,利用GM(1.1)模型的预测值与自适应阀值比较辨识和修复野值点,然后通过新陈代谢的方法利用新息代替旧息实现等维模型滚动预测。
2 灰色自适应野值检测与修正算法设计
灰色理论是由中国学者邓聚龙教授1982 年创立的,它是主要研究少数据、贫信息不确定性问题[7~8]。灰色预测具有不需要大量的样本、样本不需要有规律性分布、计算工作量小等特点。使用该方法建模只要4 个以上的数据即可,且无需知道原始数据分布的先验特征[9]。
2.1 建立灰色预测模型
灰色预测模型GM(1,1)是最常用的预测模型[10]。记原始数列为,一次累加生成得到,紧邻均值生成序列为,其中
建立灰色微分方程x(0)(k)+az(1)(k)=b ,其中a、b 为未知参数,由最小二乘估计得

将计算求得的参数a、b 代入,求解微分方程得到x(0)(k)的还原值,即

2.2 灰色等维新息模型
定义1 令x(0)(1,k) 为x(0)(k) 的k 维子列,为 模 型 预测值,则有:
2)GM(1,1)的滚动建模过程用下述符号算式表示为x(0)(k)→( a,b ),x(0)(k)→GM(1,1)模型。
GM(1,1)∑称 为的所有滚动建模,GM(1,1)∑=(G M(1,1)1,GM(1,1)2,…,GM(1,1)n-4)。式中:GM(1,1)i为第i 时刻点的滚动建模。
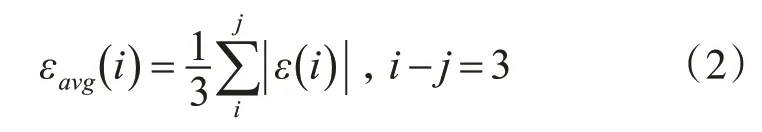
2.3 自适应野值检测与修正方法
一般地,弹道测量数据是连续变化的,经过等间隔的数据采集后获得的数据时序信号,其数据间的变化也不应该有突变[11]。根据数理统计原理[12],动态信号的时序数据具有在一定阀值范围内变化的特征,若令阀值为W ,则当时,被认为是序列中的野点,应予以剔除,由取代x(0)(i +1) 成为有效点。
定义2 对4 维新陈代谢子列x(0)(i,j) 且i-j=3 ,求出其等维新息预测一次差平均值即εavg( i ),再乘以系数k 来确定W 值,当 |δ( k+1) |>W时,即认为是数据序列中的野点,应予以剔除。W 用公式表示为

式中:k 为经验取值系数,在不同试验对象和测量系统中k 值的确定可通过几次试算来获得,经工程数据验证,取4~5较合理。
应当注意的是,在实际应用中,当连续判断异常数据数量或连续数据丢失数量超过最大允许值时,模型会失效。需要考虑参数采样频率和目标运动状态等因素,设置允许最多连续异常判断次数为Nrmax,允许最大连续丢失数量为Nlmax,当采样频率较高,目标动态变化较平稳时,可适当增大Nrmax与Nlmax值,反之应相应减小Nrmax与Nlmax值。
3 灰色自适应野值检测与修正算法流程
1)依据测量数据质量,设定允许最多连续异常判断次数和允许最大连续丢失数量。
2)对初始数据进行可用性判断,直到连续满足条件数据数量符合要求。
3)将待检测数据建立4 维灰色GM(1.1)预测模型,利用式(1)计算还原预测值。
4)计算4维数据序列的一次差平均值,利用式(2)确定当前数据野值剔除门限。
5)依据门限比较预测数据与原始数据,判断数据异常情况。
6)如果数据正常,数据序列向前滚动,去掉最早时刻的历史数据,仍保持数据序列的长度不变。
7)当某点数据判断为异常时,用预测值修复原始数据序列,向前滚动,得到新的4维数据序列。
8)当被连续判断为异常的数据数量或连续丢失数据数量超过预设值时,表明当前模型失效,进行分段处理,在各数据段内分别完成数据检测。
9)判断是否是最后一点,否则重复3)~8),直到最后一点。
程序流程见图1。
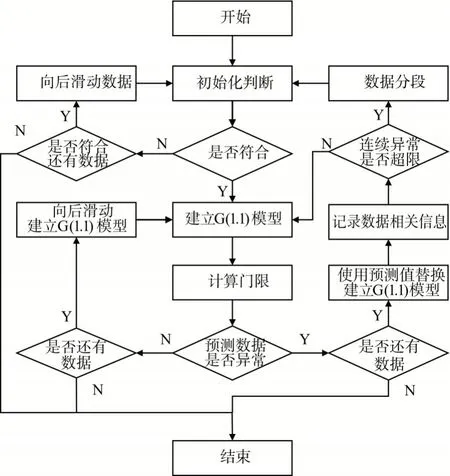
图1 程序流程图
4 仿真计算
为了定量分析利用灰色新息自适应方法对测量数据野值的检测与修正效果,选取某次靶弹仿真飞行数据,以靶弹的位置信息作为估计量,截取等间隔采样的1250 个点,飞行轨迹如图2 所示,图中X,Y,Z 分别为靶弹发射坐标系下的x 方向位置信息,y方向位置信息,z方向为位置信息,为验证该方法的野值检测效果,在x,y,z 方向分别随机生成了20 个振幅为300 的随机误差值。图3 为随机生成野值点的分布情况,横坐标为采样点序列,纵坐标为随机生成数的跃升值。

图2 靶弹仿真飞行轨迹
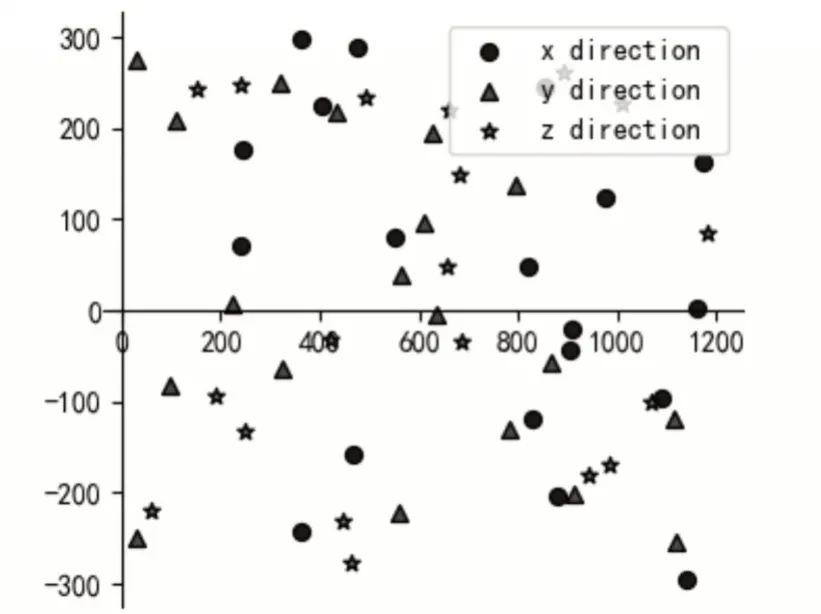
图3 随机生成野值点分布情况
利用本文方法对置入野值的位置信息参数进行检测与修正,效果如图4 所示。在x 方向呈单调趋势,检测效果较好,对随机生成的野值点检测出19 个,未检测出的随机数跃升值为2,跃升率不足0.25%,差异性较小,工程中可忽略不计;y 方向变化平缓,对随机生成的野值点检测出18 个,未检测出的随机数跃升值分别为8、-5,跃升率不超过1.1%,不影响趋势判定;在z 方向,因靶机进行大机动飞行,变化剧烈,曲线前后趋势差异明显,通过自适应阀值的控制,对随机生成的野值点检测出17个,未检测出随机点跃升率不超过3.3%,可进行后续数据的快速处理。图4 标识出未检测出随机生成野值点的位置。
从表1 中可以看出,对x 方向随机生成的野值点辨识率为95%,最小识别野值点的变化率为跃升值大于1.5%,对y方向随机生成的野值点辨识率为90%,最小识别野值点的变化率为跃升值大于1.4%,对z 方向随机生成的野值点辨识率为85%,最小识别野值点的变化率为跃升值大于6.5%,三个方向识别率平均达到90%,最小野值检测变化率为6.5%。通过多次仿真分析,可以得出该方法在一般弹道数据处理中,野值点的综合识别率可到达92%以上,最小野值检测比在4.5%以内,满足一般工程实践要求。

图4 野值检测与修正后的位置信息曲线图

表1 野值检测与修正结果
5 结语
在实际的工程实践中,测量数据中野值的出现是经常发生的。本文从灰色预测理论和实际应用出发,利用灰色新陈代谢模型对测量数据滚动预测与自适应门限相结合的方法,实现测量数据野值辨识与修正,通过仿真数据表明,该方法不仅可以检测孤立型野值而且对少量连续斑点型野值也有较好的辨识效果,对于随机产生的野值点,辨识和修正率达到90%,最小野值检测变化率达到6.5%,可以有效提高测量数据野值检测的准确性和改正精度,为提高弹道数据质量提供了较为灵活的方法支撑,具有较好的实际应用价值。当然,对于测量数据设备因长时间丢失目标或其它原因造成的长弧段散乱数据的修正问题,还需进一步探讨。

