循环冲击下风化花岗岩渗透性演化规律

翟 健,程新锋,刘连生,3

(1.江西理工大学资源与环境工程学院,江西 赣州341000;2.江西应用技术职业学院,江西 赣州341000;3.江西省矿业工程重点实验室,江西赣州341000)

离子型稀土矿在国内外是一种较为罕见的矿种,广泛分布在中国江西赣南等地,矿山生产方式是采用原地浸矿法对稀土进行浸取,该方法因工艺流程简单、成本较低且绿色环保等优点,被广泛用于渗透性较好的矿体[1-2],但是在低渗透矿体使用时,会出现淋洗时间长、浸取效率低等缺点。由于低渗透风化花岗岩型稀土矿床在原地浸矿过程中的诸多突出矛盾[3],严重制约了离子吸附型稀土矿的开发利用。由此可见,矿体渗透性会影响稀土浸出效率。矿体渗透性受多种因素影响,而孔隙结构是影响矿体渗透特性的重要因素之一[3]。孔隙结构的分布能直接影响储层的渗流能力及矿产回采的产能[4],针对此情况,笔者认为稀土矿矿床增渗机制研究可借鉴低渗透油田“层内爆破增渗”思想[5-6],在保证矿体稳定的前提下,利用小药量空气间隔爆破产生的应力波对岩石形成的冲击来改变其内部孔隙结构,从而提高矿体渗透率,达到高效回采效果。在实际工程中,要达到爆破增渗效果可能需要多次爆破作业,周围的岩石会受到循环荷载作用[7],因此,研究循环冲击荷载作用对岩样渗透特性的影响机制,在矿山高效、安全生产方面具有重要意义。

目前,岩石变形—渗流研究是围岩稳定建设的基础性课题[8],国内外学者[9-11]对岩石所受应力与其渗透率变化的关系进行了相关研究,荷载作用会通过改变岩样形状及内部构造的方式影响其渗透性[12]。Norishand[13]研究表明,应力-应变-渗流场耦合的方式在岩体渗透特征研究领域较为适用,为岩体渗透性影响机制研究开辟了新思路。Zhang等[14]通过分析岩石变形过程中渗透性演化规律,得出应变与渗透性呈正相关的结论。王环玲等[15]发现岩体环向与轴向变形相比具有更灵敏的渗透性反映能力。张天军[16]对不同恒载加压下的砂岩进行渗透性和稳定性的研究,得出有效应力与变形对砂岩渗透性的影响,表明不同变形模式或加载程度对渗透性影响作用互为不同。岩体渗透性不仅受冲击荷载强度影响,同时还受其所处环境的围压及上下渗流压差等因素影响[17]。肖伟晶[18]以红砂岩为研究对象,分析出岩石在三轴压缩过程中渗透性演化规律。陈振振等[19]采用分析变形相关渗透系数的方式,模拟岩石在高围压条件下的渗透特性,根据试验得出岩石渗透系数变化与变形密切相关。Wang等[20]研究围压对岩土混合物渗透性的影响,得出土体基质与岩块之间的作用变化直接影响其渗透性。以上试验多侧重于全应力-应变过程中围压值对岩石渗透性影响的研究,对循环冲击荷载作用下岩石渗透性演化规律鲜有提及。

1 试验

1.1 试验设备

试验利用分离式霍普金森压杆实验系统(见图1)对岩样进行冲击,该系统主要装置包括动力系统(由氮气瓶和纺锤形冲头组成)、数据检测系统(由激光测速仪、应变片、动态应变仪组成)、动荷载传递系统(由纺锤形冲头、入射杆、试样、透射杆和缓冲杆组成)。

其原理是通过高压氮气对冲头施压撞击入射杆,记录入射杆和透射杆上电阻应变片的电压值,分析岩样的应力、应变特征[22]。

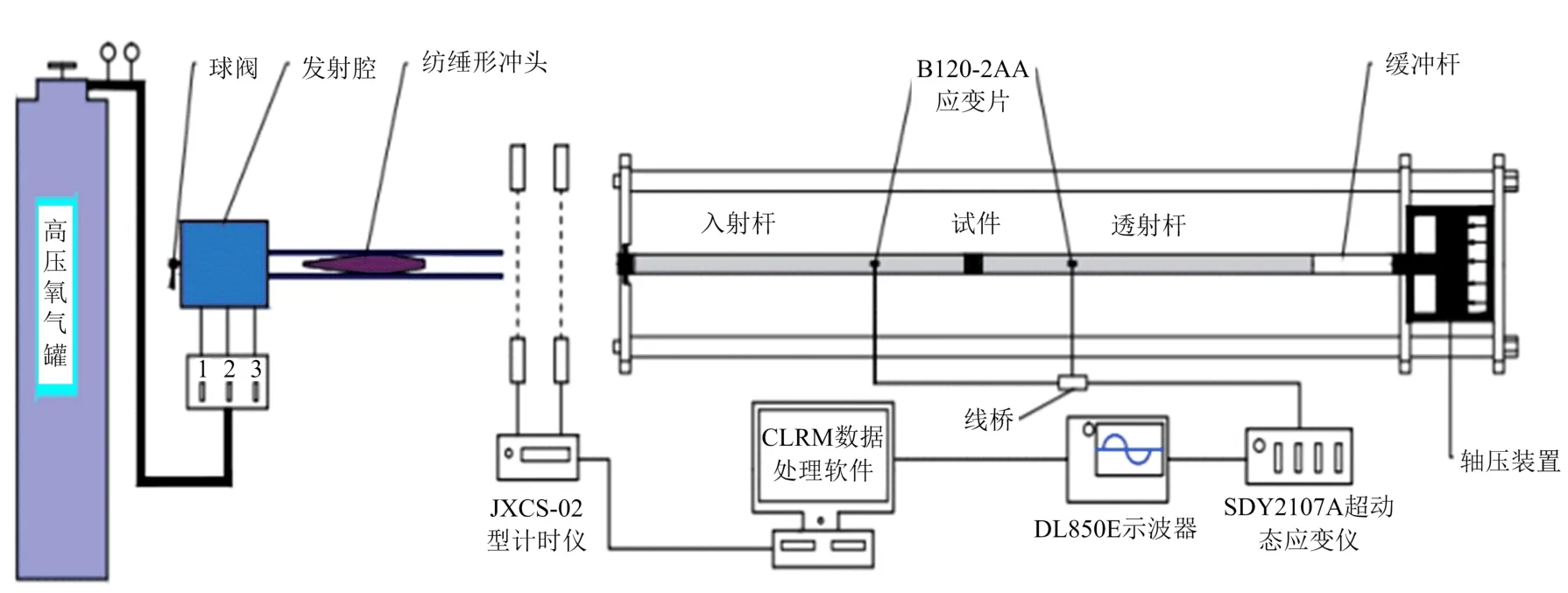
图1 分离式霍普金森杆Fig.1 Separate Hopkinson rod

本试验使用GDS-VIS三轴流变仪(英国GDS公司)研究循环冲击前后岩样的渗透能力变化特征,仪器组成如图2所示。岩样渗透率的计算是基于Darcy定律,采用进水流量稳态法,即保证岩样上下压差持续保持在一固定值范围内,通过测量稳定渗流阶段的某一时间段内渗入岩样的流体体积的变化量来获取渗透率[23],如:

式中:Q为单位时间内流体通过岩样的流量,m3/s;μ为液体的粘度系数,取1.0×10-3Pa·s;L为岩样的长度,m;A为流体通过岩样的横截面积,m2;ΔP为岩样上下压差,Pa;K为单位时间内岩石的渗透率,m2。

图2 GDS-VIS三轴流变仪Fig.2 GDS-VIS triaxial rheometer

1.2 试样制备

试样均取自赣南某离子型稀土矿含有稀土元素且埋深为10 m的弱风化层,静载抗压强度平均值为18.1 MPa。该矿山的岩石形成于燕山早期并且属于粗粒黑云母花岗岩,其包含长石、石英、黑云母以及黏土等矿物成分。所选取的岩块均是发育较为完整并且没有明显裂隙,后期经过钻取、切割工序制备成粗样,然后根据《水利水电工程岩石试验规程》(DL/T 5368-2007)[24]中的标准进行打磨,以50.00 mm×50.00 mm(直径×高)的圆柱体为标准制作试样,但试样制作过程中会存在误差,岩样基本参数如表1所示。

表1 岩样基本参数Table 1 Basic parameters of rock samples

1.3 试验方案

1)通过计算强制吸水率的方法[25]获取岩样有效孔隙度,将完整性较好的岩样选出并分为A、B、C组,每组含有4个岩样且有效孔隙度近似为2.5%、3.8%、5.5%和6.7%的递增趋势。

2)相关研究表明[26],对岩样施加的动荷载要大于其单轴抗压强度的60%～70%时才会产生有效损伤,但荷载过大又可导致岩样直接粉碎。因此,取备用岩样以近似4、5、6、7、8 m/s的速度进行单次冲击试验,得到岩样破碎冲击速度的临界值为7 m/s。为准确控制后续冲击速度,对A、B、C组岩样分别以4、5、6 m/s的冲击速度进行等速致裂循环冲击,相对应的入射能分别为12、18、24 J。

3)对冲击前后的岩样分别进行三轴渗流试验。岩样埋深10 m,故将轴压设为0.25 MPa;依据稀土矿山原地浸矿法实际应用情况,将渗压压差恒定在0.6 MPa[27],根据试验操作要求,围压值设定为2 MPa,略高于孔隙水压恒定值。

(4) 为保障施工质量和优化支护设计，确保钢拱架受压变形可控，还需进行围岩变形监测，施工监测每天不得少于1次，在拱架变形严重、围岩过渡段、注浆前后等特殊时期每日检测不得少于2次。

2 结果及分析

在保证矿体稳定的前提下,对循环冲击过程中岩石的变形特性、冲击致裂后破坏效果及初始有效孔隙度演化与渗透性之间的关系进行分析。

2.1 岩样力学特性与破坏效果

应力-应变曲线的变化趋势是研究岩石力学特性最常用的方法。材料性质、裂隙发育情况和施加荷载大小等因素,均影响应力-应变曲线的特征[28]。由A-4、B-4和C-4岩样完整循环冲击试验得到的应力-应变曲线及冲击致裂破坏效果如图3所示。

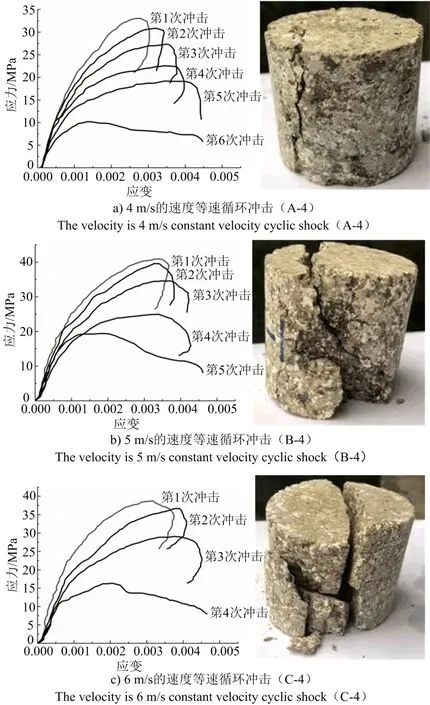
图3 岩样应力-应变曲线及破坏效果Fig.3 Rock sample stress-strain curve and destructive effect

由图3可知,以4、5、6 m/s的速度对岩样进行冲击后,其应力-应变曲线均可表现出以下阶段:压密阶段、弹性变形阶段、非线性弹性阶段及卸载阶段,岩样在动荷载作用下发生宏观损坏前,其应力-应变曲线均会表现出“回弹”现象。随着循环冲击次数的增多,峰值应力大体呈现减小趋势,而应变值逐渐增加,这说明循环冲击荷载作用会使岩样内部出现疲劳损伤现象,导致其抗冲击能力逐渐减弱,并且此损伤过程不可逆;通过图3中各循环冲击结果比较发现:随着等速循环冲击速度的提升,岩石破碎越充分,这是因为当循环冲击速度较小时,只有少数裂隙可被激活;随着冲击速度的增大,除孔、裂隙激活数量增加外,多余能量在岩样内部多次反射产生塑性变形。细观上表现为孔与裂隙的扩展、延伸和新的微缺陷的萌生;宏观上为破损越充分。

2.2 循环冲击荷载下渗透性变化规律

岩样受冲击荷载作用后,内部孔隙结构发生变化,进而改变岩样的渗透性能。为研究等速循环冲击荷载作用对岩样渗透性能的影响,将冲击前、后渗透率变化关系绘制成图进行分析(见图4)。

图4 等速循环冲击前、后渗透率变化规律Fig.4 Changes in permeability before and after constant velocity cycling

由图4可知,A组岩样渗透率在首次冲击后逐渐变小,第2次冲击后只有岩样A-2的渗透性有所回升,其余3个岩样渗透性继续下降,而在第3次冲击荷载作用下,岩样渗透性整体提升并且优于初始渗透性,此后每次等速冲击荷载均对整组岩样渗透性起到优化作用,直至其表面出现宏观裂纹;B组岩样在首次5 m/s速度冲击之后,渗透性能出现与A组岩样首次冲击后相同的下降现象,但与A组岩样渗透性变化趋势不同之处在于,B组岩样仅在第2次冲击荷载作用后便出现渗透性整体改善现象,同时后续每次等速冲击荷载作用同样优化整组岩样渗透性能,至岩样出现宏观裂纹或者破损为止;C组岩样的渗透性在整个等速循环冲击过程中均未出现减弱现象。

由于岩样在首次冲击前进行过1次渗透试验,在试验条件稳定时,流体持续流过岩样导致在其内部形成1条良好的流通通道,届时岩样外部受到一定速度冲击会将其内部渗流通道压窄,导致流体渗透岩样难度增大。因此,首次冲击后A、B组的岩样渗透性出现减小现象,当后续冲击产生的荷载累积到一定程度时,岩样内部微小的闭合裂隙会被扩展甚至贯通形成新的通道,在后续冲击过程中出现宏观裂纹或被完全破坏的情况,故岩样所受荷载作用较弱时,其渗透性会出现先衰减后持续增加的现象;而C组岩样进行试验的冲击速度大于A、B组,其荷载作用可直接将原有的微小裂隙通道延伸,甚至可将多条通道相互贯通,致使后续进行渗透试验时流体更易于渗过岩样,此冲击速度可作为稀土矿山实际增渗工程的一个参考。

2.3 岩样初始有效孔隙度与渗透率关系

有效孔隙度特指岩样内部相互贯通的微孔隙体积之和与岩样总体积之比,其在一定程度上可以反映岩样内部裂隙的发育程度。岩样裂隙发育愈加完整,流体更容易渗过岩样,二者之间的关系如图5所示。

图5 岩样初始有效孔隙度与渗透率关系Fig.5 Relationship between initial effective porosity and permeability of rock samples

从图5可以看出,在渗透试验条件一致的情况下,岩样渗透率随其初始有效孔隙度的增加整体呈现上升趋势,说明岩样有效孔隙度对其渗透率大小有决定性影响,但二者之间并未有严格的函数关系。通过分析有效孔隙度相近岩样的渗透率,发现有效孔隙度偏大的岩样反而出现渗透率减小甚至大幅度衰弱的现象,这与邵维志等[29]所研究的岩石有效孔隙度微小改变可能会引起渗透率数量级变化的结论一致。岩体是一种无规则不均匀的自然介质,长期风化作用导致其内部孔隙分布杂乱无章,因此孔隙开口方向存在不确定性;同时试验仪器的出水口及进水口分别位于岩样上、下两端,当裂隙发育方向与轴向平行时,流体更容易渗过岩样;当裂隙方向垂直于轴向时,轴向荷载压力会将裂隙压密,阻碍流体渗透岩样。有效孔隙度大小虽能反映岩石内部相互贯通的孔隙数量的多少,但难以确定岩石内部孔隙、孔径大小。这意味着岩样渗透率不仅受其有效孔隙度及孔隙开口方向的影响,同时较小的岩样颗粒及孔隙、孔径均会对流体在岩样渗透过程中起到一定抑制作用,但有效孔隙度对岩体的渗透性影响最为直接。

2.4 岩样初始有效孔隙度与增渗效果关系

初始有效孔隙度是岩样受冲击荷载作用前渗透性最直接的影响因素,而岩样渗透性后期改良程度则由冲击荷载作用决定。由于A、B组岩样渗透性在冲击后均出现不同程度的衰弱现象,将C组岩样试验结果作为研究参数,而C组岩样中仅有C-1在第4次冲击后保持完整,其余3个岩样均在第4次冲击后破损,无法进行后续渗透试验。故本次总结未将岩样C-1的渗透性变化率纳入分析范围内,岩样初始有效孔隙度与冲击后渗透性变化率关系如图6所示,其中图6a反映C组岩样在每次冲击后渗透性与本次冲击试验进行前渗透性的变化率,图6b为岩样冲击后渗透性变化率总和的平均值与初始有效孔隙度之间的关系。

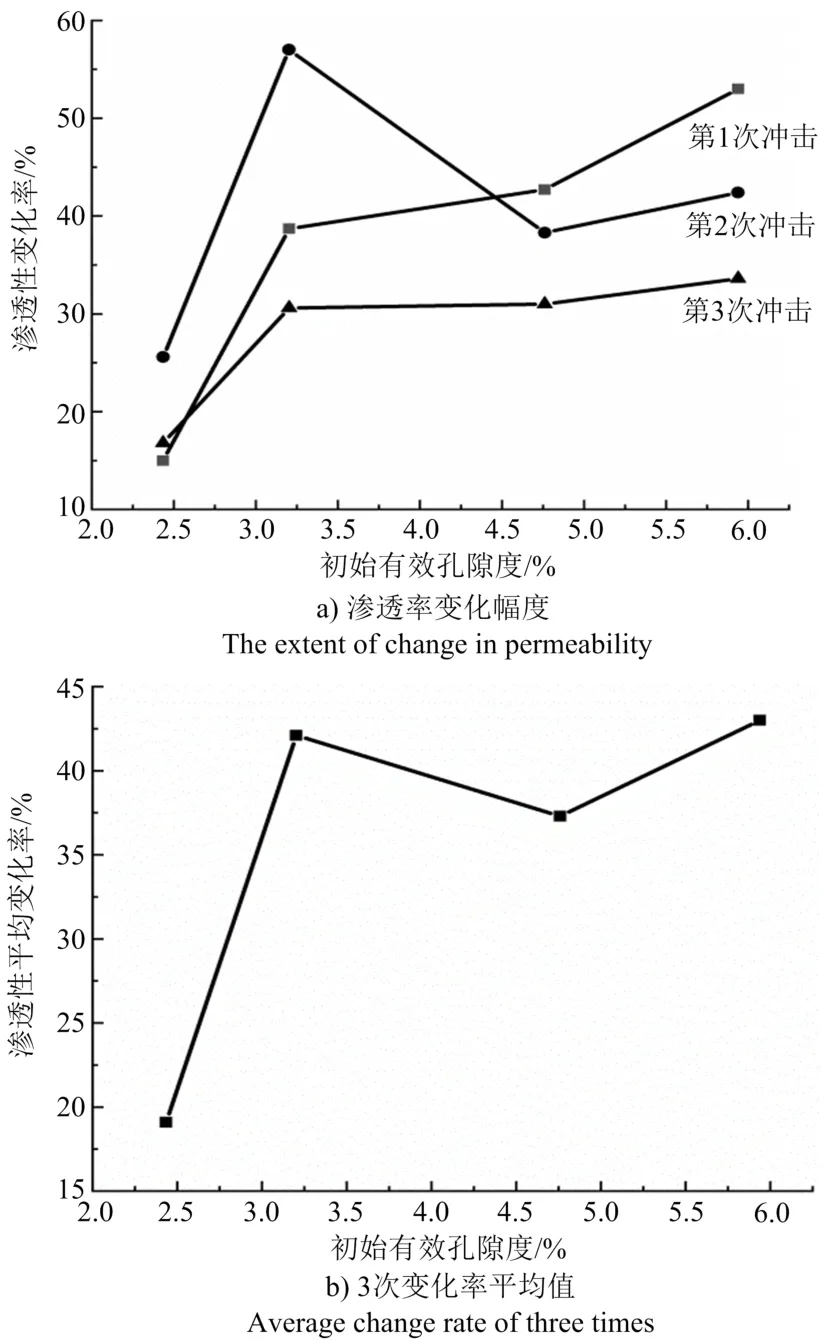
图6 岩样初始有效孔隙度与渗透率变化关系Fig.6 Relationship between initial effective porosity and permeability of rock sample

由图6a可知,每次冲击荷载作用后,C组岩样渗透性变化率均为正值,说明冲击后渗透性均被优化,同时随着岩样有效孔隙度的增加,增渗幅度逐渐变大;图6b所表示的3次冲击变化率平均值同样反映岩样渗透性优化效果,整体随初始有效孔隙度增大而增大。岩样初始有效孔隙度越小,其内部裂隙纹路相对较短;相反,有效孔隙度较大,岩样内部的裂纹通道相对更长。当两种内部裂纹构造分布不同的岩样承受相同冲击荷载作用时,内部均会出现裂纹蔓延及微小裂纹相互贯通的现象。依据Griffith理论,长裂纹与短裂纹相比,更易发生扩展,同时微小裂纹贯通后其内部渗流通道更为明显,初始有效孔隙度较大的岩样在冲击后裂纹扩展更为明显。因此冲击后增渗效果更加显著,这一现象持续至岩样破坏。

3 结论

1)随着循环冲击次数的增多,风化花岗岩的疲劳损伤会导致峰值应力减小而应变值逐渐增大,同时其抗冲能力逐渐减弱,并且此损伤过程不可逆,岩样破损后碎块数量与冲击速度成正比。

2)速度4、5、6 m/s的等速循环冲击对风化花岗岩渗透性变化趋势影响不同。4、5 m/s的速度等速循环冲击会使岩样渗透性先减小后变大,而6 m/s的速度等速循环冲击会使岩样渗透性能持续优化至岩样完全损坏。

3)在相同渗透试验条件下,岩样渗透率随其初始有效孔隙度的增加呈现上升趋势,说明岩样有效孔隙度对其渗透率大小有影响,然而这种变化趋势并不绝对,内部孔隙开口方向及孔径大小的不确定性,会导致岩样出现孔隙度增大而渗透率减小甚至大幅度下降的现象,但有效孔隙度可直接影响岩体渗透性。

4)岩样初始有效孔隙度越大,其内部孔隙结构在同等冲击荷载下更容易发生变化,同时岩样在后续冲击荷载作用下增渗效果与初始有效孔隙度密切相关,初始有效孔隙度越大,在后续冲击荷载作用下增渗效果愈加明显。

由此可知,矿体在6 m/s的冲击速度下增渗效果最佳,此冲击速度可借鉴至离子型稀土矿山实际增渗工程,为保证矿体稳定,爆破次数应控制在3次以内。此速度对应的入射能为24 J,岩样吸收能平均为7 J,该能量可作为爆破现场所需炸药量的换算依据。