基于改进人工势场-模糊算法的路径规划算法研究

汪四新, 谭功全, 罗玉丰, 樊 石

(四川轻化工大学自动化与信息工程学院, 四川 自贡 643000)

引 言

移动机器人面临的首要问题就是如何有效快速地到达目标点，并且能躲避路途中所遇障碍物。路径规划是机器人导航中最基本的问题[1-2]，指的是如何规划出一条由出发位置到目标位置的无碰撞适宜轨迹。路径规划分为局部路径规划和全局路径规划[3]，局部路径规划指的是环境未知情况下的避障运动规划，全局路径规划则是在环境已知的情况下搜索全局最优的路径规划。常用的全局路径算法主要有栅格法[4]、A＊算法[5]、RRT[6]以及仿生群搜索算法[7-8]等。常用的局部路径规划算法有动态窗口法DWA[9]、人工势场法等。

人工势场法利用障碍物和目标形成的势场来牵引机器人运动，因此拥有非线性特点，使得运动轨迹平滑，但容易出现目标不可达和陷入局部极小值问题。刘俊雅[10]在斥力中加入欧几里德距离函数并提出了一种基于情景行为的障碍物连接法，有效解决了目标不可达与局部极小值问题，但在凹型障碍物中，机器人还会产生徘徊。针对复杂环境中机器人容易产生剧烈震荡及局部最优，有学者采用模糊人工势场对势场参数进行模糊决策处理[11-12]，但未能完全克服机器人剧烈震荡问题。韩伟[13]在此基础上提出了一种基于模糊人工势场法的动态路径规划，避免了复杂环境中的剧烈震荡，但在凹型障碍物中仍存在明显徘徊、波动。考虑以上问题，本文在改进斥力基础上，利用模糊输出力调整改善运动轨迹。仿真结果表明，本文方法避免了目标不可达，跳出了局部极小值点，在凹型槽中无徘徊且震荡较小。

1 人工势场法

1.1 传统人工势场模型

传统人工势场法是由Khatbi[14]于1985年提出的一种路径运动算法。人工势场是将路径规划中的机器人运动模式与自然界存在的各种势场对应起来，机器人运动目的就是到目标点，中途要躲避障碍物，因此让目标点对机器人提供吸引势场，障碍物对机器人提供排斥势场，在两种势场相互作用下，机器人就能比较平滑稳定地到达目标点。因此可以定义出机器人的所受总势场为：

U(X)=Uatt(X)+Urep(X)

(1)

式中：Uatt为目标点提供的吸引势，Urep为障碍物提供的排斥势。

机器人受到引力的牵引而向目标点移动，因此机器人与目标的距离与引力应该成正比关系，距离目标点越远所受的引力应该越大，目标点处引力为0，因此定义引力势场Uatt(X)如下：

(2)

式中：Katt为引力常数，ρg表示机器人矢量位置与目标点矢量位置的欧几里德距离。

引力函数即为引力势函数的负梯度，方向是由机器人指向目标点，引力函数如下：

Fatt(X)=-▽Uatt(X)

(3)

(4)

机器人在往目标点运动过程中要躲避障碍物，障碍物给予机器人的就是斥力作用，因此机器人与障碍物的距离与斥力为反比关系，距离障碍物越近障排斥力越大，斥力势场Urep(X)如下：

(5)

式中：Krep为斥力常数，ρr为障碍物矢量位置与机器人矢量位置的欧几里德距离，ρ0为障碍物最大影响距离。

同样斥力势场的负梯度即为斥力函数，方向由障碍物指向机器人，斥力函数如下：

Frep(X)=-▽Urep(X)

(6)

(7)

1.2 改进斥力人工势场模型

针对传统人工势场法容易陷入目标不可达的问题[15-16]，对斥力场进行改进，加入机器人与目标点欧几里德距离的对数，并将对数左移一个单位，使得机器人在目标点对数函数值为0。改进的斥力势场函数如下：

(8)

在新排斥势场中，机器人受力如图1所示，对排斥势场求负梯度可得排斥力，将排斥力Frep分解为两个分量，Frep1分量由障碍物指向机器人，Frep2分量由机器人指向目标点。

图1 机器人在新势场中受力分析图

斥力函数公式如下：

(9)

由两分量的方向，Frep1为Frep对ρr求导，Frep2为Frep对ρg求导，公式如下：

(10)

(11)

对改进斥力的函数加入一个基于机器人、障碍物、目标点3个坐标计算的判据，定义机器人位置坐标(X,Y)，障碍物位置坐标(Xr,Yr)，目标点坐标(Xg,Yg)，判据公式如下：

M=XYr+XrYg+XgY-XYg-XrY-XgYr

(12)

当M≤1时，代表机器人陷入了局部最优或者死循环，此时通过加大沿障碍物到机器人方向斥力分量Frep1的Y坐标轴分量到原来的10倍，使之有效逃离局部最优。

2 改进人工势场-模糊算法

在人工势场中加入模糊算法，采用TS(Takagi-Sugeno)模糊模型。通过计算出引力与斥力的角度差以及斥力与引力的合力差，将这两个差量模糊化，作为模糊决策的两个输入量，通过模糊规则得到一个TS模糊输出量，定义这个输出量为模糊力Ffu，分解Ffu到X轴方向和Y轴方向，再将分解的两个分力与未加模糊控制前的分力相叠加，进而调整机器人合力大小与方向，使得机器人能协助逃离局部最小点并且轨迹更加平滑稳定。

2.1 模糊输入

分别计算出引力、斥力夹角，根据夹角的定义，其为最小正角，所以要将计算出的夹角还原成真实的象限角。判断出夹角处于的象限，若夹角处于一象限则不处理，若夹角处于二、三、四象限则象限角分别如下：

θ1=π-θ

(13)

θ1=π+θ

(14)

θ1=2π-θ

(15)

式中：θ1为象限角，θ为引力或斥力夹角。

计算出引力与斥力的合力差，并分别对角度差限幅(-π,π)，合力差限幅(-1,1)，超出部分等于边界值。

将两个模糊输入分为五个模糊语言变量{负大(NB)，负中(NM)，零(Z)，正中(PM)，正大(PB)}，角度差论域为(-π,π)，合力差论域为(-1,1)，隶属度函数采用三角形隶属度函数，角度差θ与合力差e的隶属度函数如图2所示。

图2 模糊输入隶属度函数

2.2 模糊决策

将设定好的模糊输入通过表1给出的模糊规则决策，得到模糊输出。因为使用的是TS模糊模型，模糊输出值为确定常数值，不需要进行解模糊化，且模糊输出Ffu对应的5个常数值分别为mf1(-1)，mf2(-0.5),mf3(0),mf4(0.5),mf5(1)。

表1 引力与斥力角度、合力差值模糊规则

2.3 合力重计算

为了使模糊输出力对机器人有良好的效果，将其扩大到50倍，并设定模糊输出夹角为原合力夹角加0.5π：

θfu=θt+0.5π

(16)

式中：θfu为模糊输出夹角，θt为原合力夹角。

将模糊输出力分解到X轴分量Ffux和Y轴分量Ffuy，再与模糊控制前的分力相叠加，进而形成新的合力F与合力夹角αt，公式如下：

Fx=Fattx+Frep1x+Frep2x+Ffux

(17)

Fy=Fatty+Frep1y+Frep2y+Ffuy

(18)

(19)

3 仿真实验及分析

在Matlab软件中进行仿真实验，并利用其中Fuzzy工具箱完成模糊控制系统设计。通过搭建一个10×10的地图，添加好机器人坐标、目标点坐标以及若干障碍物坐标。对比以往势场法与逐次改进的方法，通过仿真得到路径、合力、斥力图，分析机器人陷入目标不可达和局部极小值问题，以此证明本文方法的有效性。

首先进行参数设置，为保证各方法具有可比性，初始参数设置保持一致。地图均为10×10大小，因此起点位置和终点位置分别均为(0,0)、(10,10)，引力增益常数Katt为15，斥力增益常数Krep为5，障碍物最大影响距离P0为1，对数函数幂a取为0.5，机器人步长L为0.2，以K表示机器人到达目标点的迭代次数。

3.1 散乱障碍物环境仿真

随机添加散乱分布的障碍物，障碍物个数为15，对比传统人工势场法、改进斥力人工势场法、改进人工势场-模糊算法三种逐次改进的仿真效果，如图3所示。为便于观察机器人轨迹及仿真效果，传统人工势场轨迹采用的是“.”表示方式，其他两种仿真轨迹采用的是“.-”表示方式，即在“.-”处才是机器人真实轨迹。

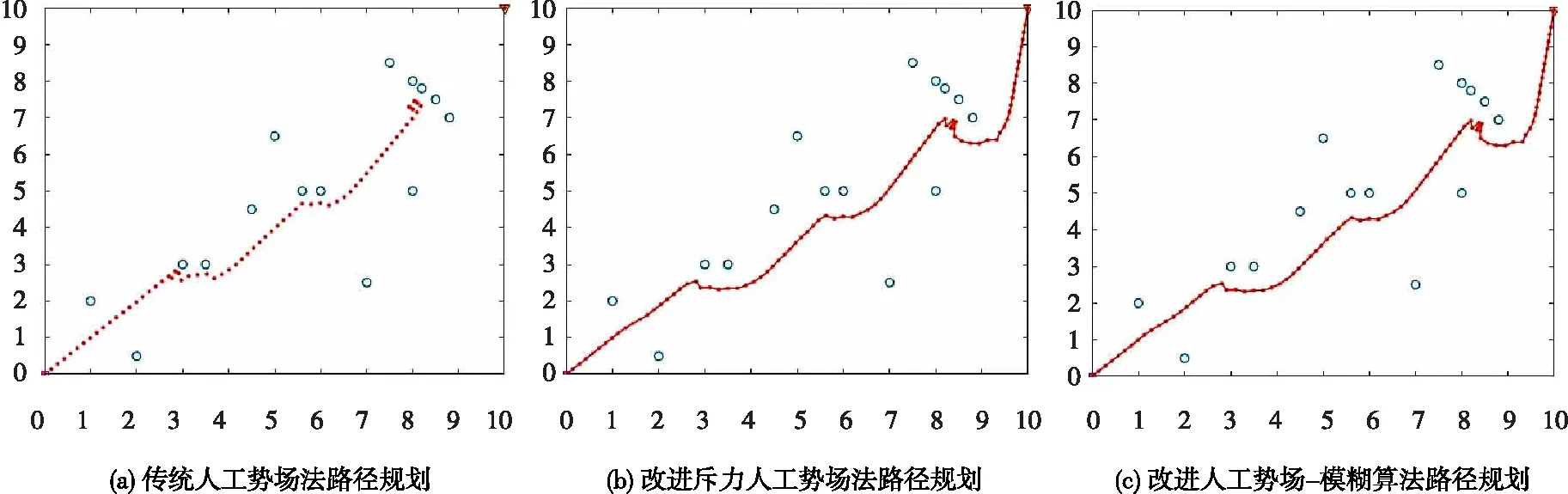
图3 散乱障碍物路径规划

传统人工势场法在目标点前面临较多密集障碍物时出现了容易极小问题，从而不能到达终点，如图3(a)所示，并在中途出现了循环轨迹，其合力分析如图4所示。由图4可以看出，机器人在x=8 cm处合力非常小，使得机器人陷入了局部极小问题，以致于机器人不能达到目标点。加入了对数函数及极小值判据的改进算法，能有效避免目标不可达，在局部极小值点时，通过改变斥力Y轴分量大小，有效逃离局部极小值点，顺利到达目标点，如图3(b)所示。改进人工势场-模糊方法能够自适应调节受力大小和方向，路径更加平滑，波动更少，稳定性更强，如图3(c)所示。三种递增式方法的仿真效果对比见表2。

图4 传统人工势场法合力图

表2 散乱障碍物路径规划仿真参数统计表

3.2 凹型槽障碍物环境仿真

传统人工势场法、改进斥力人工势场法、改进人工势场-模糊算法在经典凹槽障碍物模型下的对比仿真图形如图5所示。

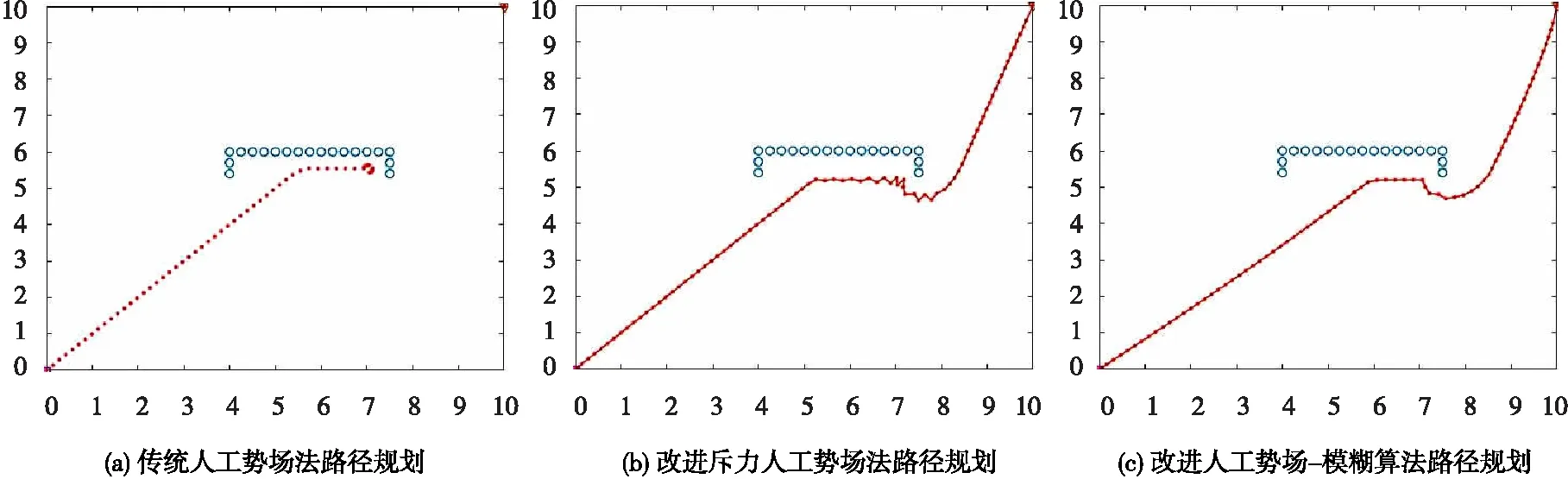
图5 凹型槽障碍物路径规划

在凹型槽障碍物环境下，传统人工势场法由于无法改变机器人的位姿状态，一旦陷入了局部问题，很难逃离，如图5(a)所示。经过改进斥力的方法，使机器人及时逃离困境，其能成功从凹槽中逃离出来并到达终点，如图5(b)所示。在此基础上融合模糊决策后的模糊力能自适应调整机器人位姿，使得轨迹更加平滑，能更快、更稳地到达目标点，如图5(c)所示。三种递增式方法的仿真效果对比见表3。由表3可知，改进后两种方法均能逃离到达目标点，但改进人工势场-模糊算法到达目标点所用迭代次数更少。

表3 凹型槽障碍物路径规划仿真参数统计表

对能到达终点方法的斥力与合力分析，分别如图6与图7所示。对应比较分析图6与图7两方法的斥力与合力可知，在凹槽连续障碍物的作用下，加入了模糊力自适应调整的机器人所受斥力和合力波动明显减少，而且在接近凹槽末端拐角x=7 cm处，由于机器人需要做出较大角度的调整，加入模糊方法后可以避免陡然剧增的受力，使得机器人能够更加安全、稳定、快速地到达目标点。

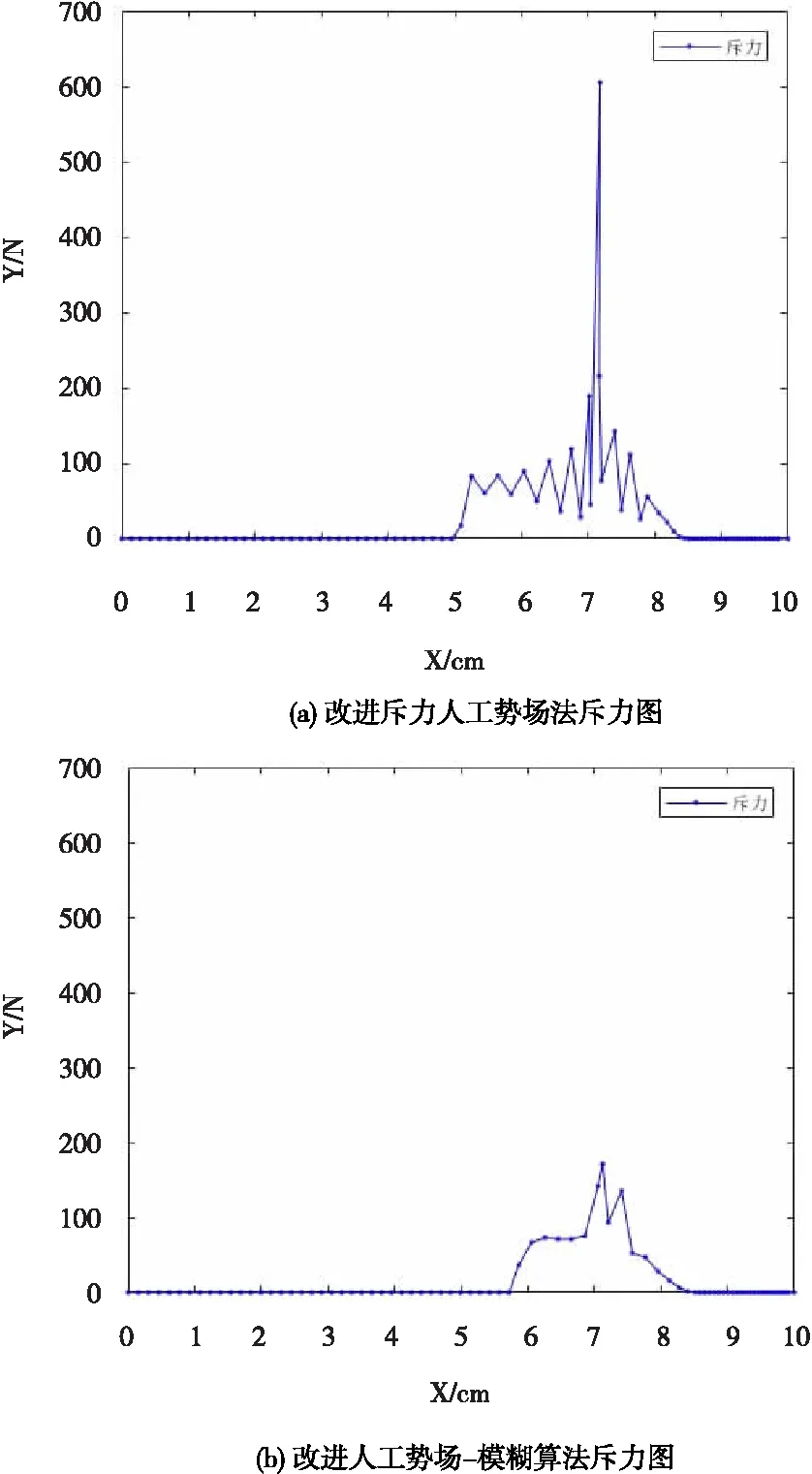
图6 斥力图

图7 合力图

4 结束语

传统人工势场法在移动机器人路径规划中容易出现局部极小值和目标不可达问题，从而无法达到目标点。本文在传统人工势场法的基础上加入欧氏距离对数改进斥力函数，避免出现目标不可达，并通过机器人、障碍物、目标点位置判据逃离局部极小值点。在此基础上结合模糊算法，使得移动机器人在完成局部问题逃离的同时路径更加稳定平滑、到达终点的迭代次数更少，尤其在凹槽障碍物地图中，有效解决了机器人徘徊及震荡问题。但在极度简单的障碍物环境和没有出现目标不可达、局部极小值问题下传统人工势场法仍快速有效。在MATLAB软件中进行了仿真，对传统方法、改进斥力人工势场法和改进人工势场-模糊算法做了对比试验，仿真结果证明了本文改进方法的有效性。