水下穿越管道附近河床演变特性试验
杨 乾 孙明楠 何 沫 杨庆华
1.西南交通大学土木工程学院 2.中国石油西南油气田公司安全环保与技术监督研究院
0 引言
穿越水域的输油气管道在管道工程当中占有相当大的比例。当油气管道穿越江河时,一般采用水下穿越和水上跨越两种方式。对于前者而言,由于河床演变、河床冲刷和水流冲击等作用,使得管道局部悬空或裸露而容易遭受破坏,从而严重影响水下穿越管道的安全服役。如1979年投产的马惠宁线渠口农场穿越黄河管道,运营不到5年便被洪水冲断,造成直接经济损失500余万元并停产21天[1]。
20世纪80年代,俞乐群[2-3]便开始了对穿越管道的研究。黄金池[4]在1998年分析了河床演变对穿越管道的影响,并提出了减少水毁灾害的相应措施。白路遥等[5]考虑河流上游洪水来沙因素重新建立了冲刷深度计算模型,为油气管道穿越高含沙河流埋深的确定提供了理论依据。唐万金等[6]依据工程实例,提出在考虑冲刷公式的基础上,应结合当地水文地质条件最终选择设计冲刷深度。张芝永[7]通过数值模拟方法提出一种预测局部冲刷平衡深度的新方法,为水下管道局部冲刷平衡深度预测提供了技术手段。Azamathulla和Zakaria[8]将人工神经网络(Artificial Neural Network,ANN)方法应用到管道冲刷深度估算中,并验证了该方法的有效性。除此之外他还研究了局部管道冲刷深度的时间变化规律,以估算冲刷深度,并提出了一种能够很好地预测相对冲刷深度的回归模型[9]。徐涛龙等[10]、姚安林等[11]、付冉等[12]和Zhao等[13]均采用数值模拟方法,对穿越管道悬空长度的动态演变过程进行了分析,得到不同工况下管道的临界悬空长度,为河流穿越管道的设计和安全运营提供了数据支撑。较之于水下穿越管道,更多的学者更倾向于研究海底管道的冲刷问题,如吴钰骅等[14]、杨兵等[15]、臧志鹏等[16]、Zhao等[17]、Kim等[18]、Rao等[19]通过物理模型试验,研究海底管道局部冲刷的发展阶段,探讨了水下管道底砂床沙粒起动的产生机理。常留红等[20]、刘延鑫等[21]、陈兵和张桦[22]、Zhao等[23]通过数值模拟研究海底管道附近流场、压力以及剪切力的变化,对海底管道局部冲刷机制进行了分析。综上所述不难发现,关于穿越管道的研究主要集中在冲刷深度预测和管道临界悬空长度计算等方面,而对于穿越管道附近河床演变过程的研究则甚少,虽然很多学者都研究了海底管道周围河床演变过程和冲刷特性,但研究对象管道均处于半埋状态,与水下穿越管道为全埋的初始条件不同,导致两者在水流作用下河床演变与局部冲刷特性相异。为此,笔者通过单向流循环水槽试验,观测分析穿越管道发生局部冲刷的物理过程和冲蚀剖面特征,研究了水下穿越管道附近河床演变规律及其对水下穿越管道的影响。
1 试验模型设计
1.1 试验装置
试验在西南交通大学市政工程实验室循环水槽系统内进行,该系统由水槽、沉沙池、清水池、水泵、阀门和回水管组成(图1)。水槽长10 m、宽0.4 m、高0.7 m,水槽侧壁均采用透明钢化玻璃制成,便于观测,水槽头部设置有梯形堰和稳流板,用于提供试验稳定流量。距稳流板下游2 m处设置试验段,全长1.5 m,试验段前后各铺设0.3 m长的由1 cm以上粗颗粒砾石组成的护坡(图2、3)。水槽尾部设置尾门,以调节水槽内试验水深。试验均在清水冲刷机制下进行,试验水温(t)为15 ℃。根据弗劳德数计算公式:
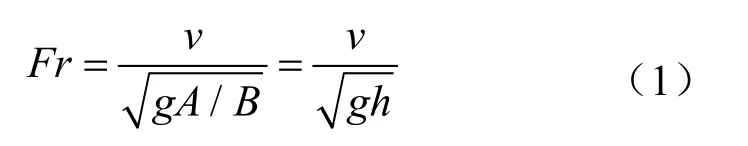
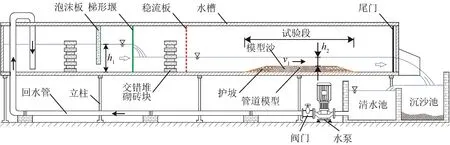
图1 水槽试验模型示意图
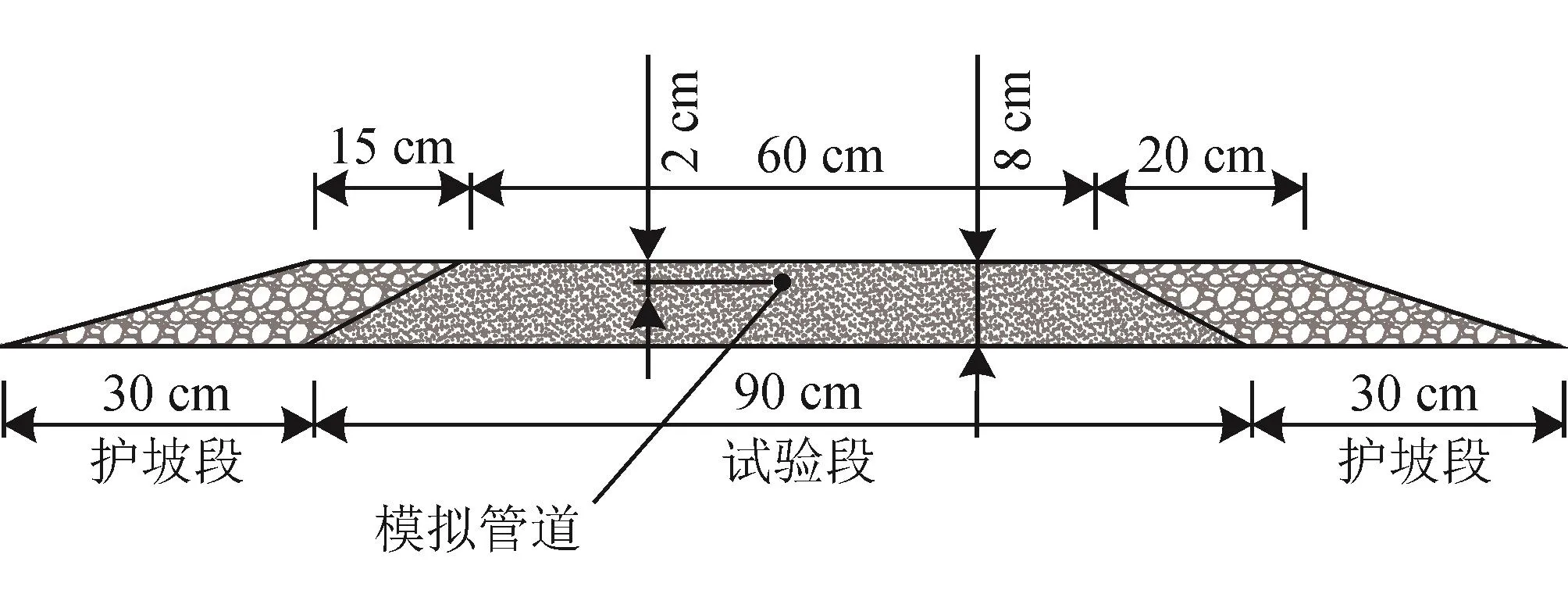
图2 试验段布置示意图

图3 试验段布置实图
式中Fr表示弗劳德数;v表示断面平均流速,m/s;A表示过流断面面积,m2;B表示渠道液面宽度,m;h表示水深,m;g表示重力加速度,m/s2。计算得到水槽试验的弗劳德数介于0.306~0.808(表3),均小于临界流Fr=1。因此本试验水流均处于缓流状态。
1.2 模型相似律
水力模型试验:在模型中重演(或预演)与原型相似的水流现象以观测、分析、研究水流运动规律,其应具有几何相似、运动相似、动力相似及初始条件和边界条件相似这些要求,但在试验过程中,要同时满足以上相似准数相等几乎不可能实现。因此,通常采用近似的模型方法,分析相似条件中的主、次关系,在模型试验设计中尽量保证起主导作用的条件,对次要条件只作近似保证或忽略不计。
由于水下穿越管道在河流冲刷过程中,惯性力和重力起主导作用,因此采用重力相似准则(弗劳德相似准则)进行水力模型设计,即:

式中λv表示速度比尺;λg表示重力加速度比尺,取1;λL表示长度比尺。根据实验室场地条件,采用正态水力模型,本次试验选定的长度比尺λL=80,试验流体采用自来水,在此基础上以单宽流量作为试验主要考虑条件,并使各个参数经长度比尺换算后得到对应的水力因素控制在合理范围之内进行试验设计,最终得到原型和模型之间对应的各物理量的比例关系如表1所示。

表1 试验参数相似比尺关系表
1.3 模型沙和模拟管道
根据DL/T 5244—2010《水电水利工程常规水工模型试验规程》关于模型冲刷材料选择的要求[24]:模拟砂砾石河床覆盖层,宜用碎石散粒体,其粒径宜按长度相似换算选择。因此,为了更合理模拟砂砾石河床的演变过程,选用石英砂作为本次试验的模型沙。根据某河流勘察得到的河床稍密卵石颗粒分析结果,按照长度比尺λL=80进行设计,得到如表2所示的模型沙颗粒级配。
模型沙颗粒级配分析得到:粒径相对比较均匀,主要集中在0.25~0.75 mm之间,根据级配曲线图得到其中值粒径d50=0.55 mm,通过量筒法测得模型沙的容重为14.39 kN/m3,根据多个起动流速计算公式[25]得到模型沙临界起动流速Vc=0.2 m/s。
试验采用管径为1 cm的空心光滑有机玻璃管作为模拟管道,试验前采用强力胶水将模拟管道两端固定在水槽边壁上,管道轴向与水流方向垂直,管道中心距水槽底6 cm,管顶覆沙1.5 cm,模拟管道位于试验段中部。
1.4 试验工况和流程
水下穿越管道冲刷是河流、河床和管道三者之间的动力耦合作用问题,国内外学者对河床演变过程的研究表明,影响冲刷特性的因素较多,相互关系较为复杂,主要受床沙组成、管道尺寸、水动力等因素的影响,由于河流水量随季节变化较大,水动力特性复杂,因此主要研究水动力条件对穿越管道附近河床演变特性的影响。
为研究不同流速和水深对水下穿越管道局部冲刷的影响,试验共设计9个组别,3组流量和3组流速对应9组水深(表3)。流量分别为4.05 L/s、5.40 L/s和 6.75 L/s,比值为 0.75∶1.00∶1.25,考虑到水流对河床的冲刷,选择3种不同流速,即0.25 m/s、0.30 m/s和 0.40 m/s,分别为起动流速的 1.25 倍、1.50倍和2.00倍。由于在水流冲刷过程中河床不断下切,流速和水深随河床演变而发生变化,因此试验工况中设计的流速和水深为河床冲刷前的试验流速和下游水深,分别对应图1中所示的v1和h2。

表2 模型沙颗粒级配表
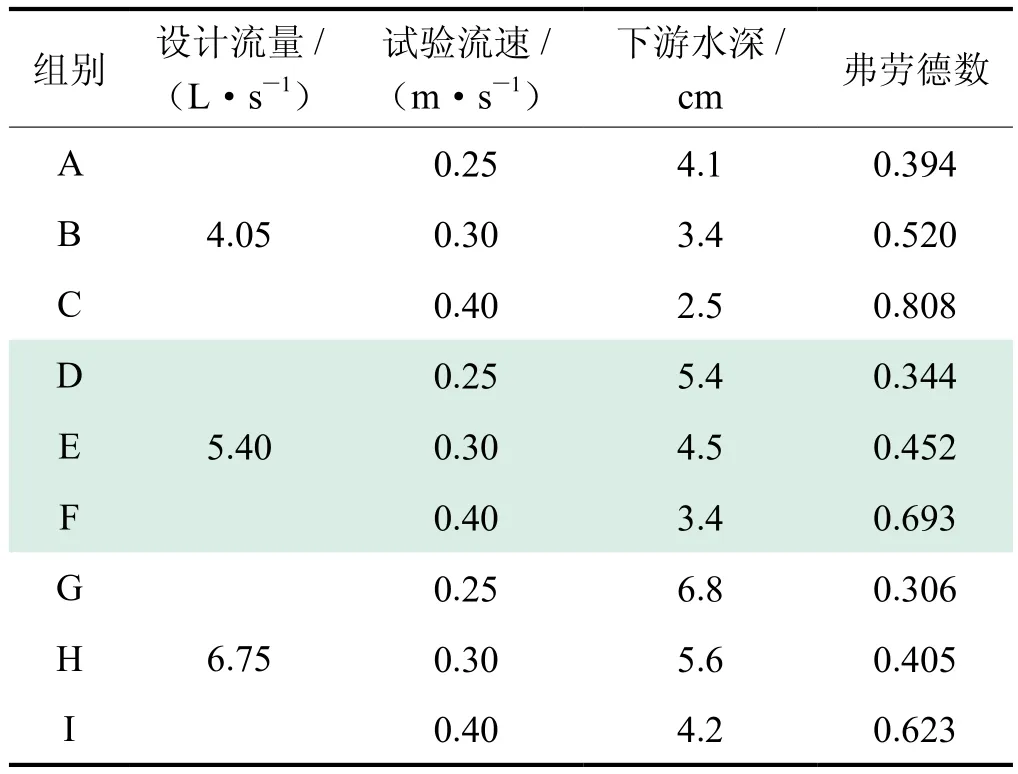
表3 试验因素水平表
试验工况确定后开始试验实施阶段,试验前根据试验段布置尺寸,采用自然沉降法进行模型沙铺设,铺沙厚度为8 cm,试验段铺设完成后,关闭水槽尾门,利用管径为1.5 cm的自来水管向水槽头部注水,水深h2达到15 cm后停止注水,静置24 h,待模型沙充分饱和后开始试验。打开阀门,启动水泵,缓慢调节阀门至设计流量(流量通过梯形堰计算公式和上游水深h1确定),然后缓慢打开尾门,调节水槽水深h2至设计水位,开始计时。采用高清数码摄像机记录水下穿越管道附近河床演变的物理过程,根据冲刷过程选取特征时间节点,记录冲刷时间,拍摄冲蚀剖面,利用探针逐点测量河床表面的位置坐标和高程(网格1 cm×1 cm,管道附近0.5 cm×0.5 cm),当达到刷冲平衡后,完成最后一次数据采集,试验结束。
2 试验结果分析
2.1 穿越管道局部冲刷过程
通过试验观察发现,9个组别的管道局部冲刷过程基本相似,但是由于在水流作用下沙粒的起动具有一定的随机性,除了与水动力条件有关之外,还与沙粒颗粒形状、位置等因素有关。因此,对于穿越管道局部冲刷过程只能通过观察定性分析,一般可分为:河床下切、管道暴露、微孔形成、冲坑扩展、管道悬空和冲刷平衡6个阶段,河床演变几何形态和冲刷特征如表4所示,部分河床演变冲蚀剖面见图4。
2.2 冲刷机理分析
水下穿越管道冲刷机理的研究本质就是分析冲刷过程中水动力条件、沙粒特性和管道位置等影响因素之间的相互关系,探究引起局部冲刷的主要因素。国内外学者对此也提出了不同的观点:Lai[26]认为由于水流在管道附近形成涡流,管道两侧流速不同,较大的水压力差导致管底出现渗流,从而引起冲刷现象产生;Mao[27]认为水流作用下管道附近的涡流是引起局部冲刷的主要因素。
水下穿越管道附近冲刷机理如图5所示,当河床下切至管道暴露后,由于管道的存在,导致管周流场发生改变,水流在管道附近形成漩涡,管道上游顺时针涡流产生上举力(FL),将沙粒带入水流中,同时FL与水流产生的拖曳力(FD)形成斜向上的合力(F),将沙粒输送至管道下游,管道下游形成的涡流继续将沙粒向下游输送。随着管周沙粒背离管道迁移,导致A区沙粒不断积累,形成河床局部隆起,B区沙粒不断减少,沙粒与管道的接触面(S)逐渐减少。由于管道上游涡流运动剧烈,前后较大动水压力差导致管底出现渗流,当S减小至某一值时,作用在沙粒上的渗透力大于浮重力,水流将沙粒带走,从而出现管涌现象,管底微孔形成,局部冲刷由此开始。因此,导致水下穿越管道产生局部冲刷的原因有涡流和渗流两方面,管道暴露前涡流使管周沙粒减少,管道暴露后涡流和渗流共同作用使管底出现微孔,从而形成局部冲刷。

表4 河床演变的形态和特征

图4 部分河床演变冲蚀剖面图
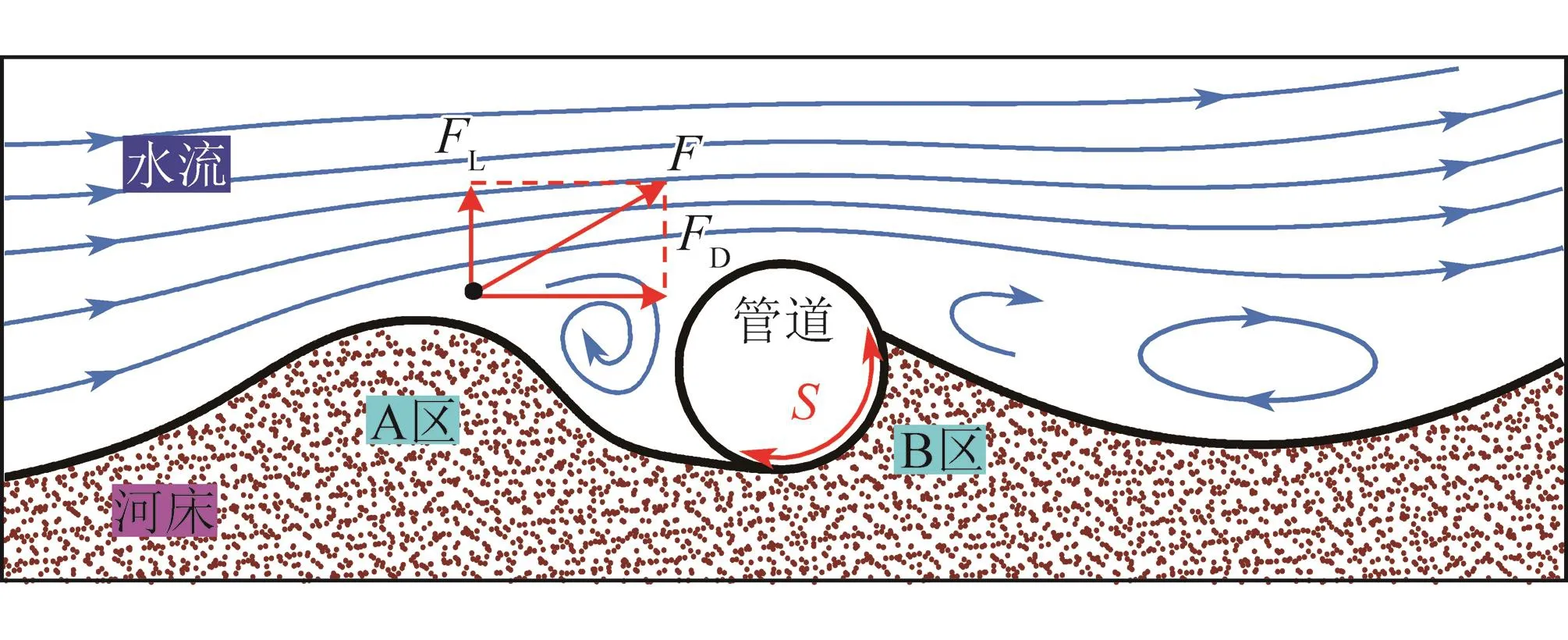
图5 管周冲刷机理示意图
2.3 水动力条件对管道局部冲刷的影响
通过上述冲刷机理分析可知,水动力条件、沙粒特性和管道位置均是影响管道局部冲刷的影响因素,根据试验代表不同工况设计,主要分析水动力条件对水下穿越管道局部冲刷的影响。即使在同一工况下,不同河床剖面的演变形态也不同,因此,选取水槽其中一侧壁面作为研究的河床特征剖面。根据高清摄像机记录的管道附近河床演变的物理过程,取管道附近20 cm×5 cm矩形窗口,绘制出不同工况下不同冲刷阶段对应的河床几何形态,如图6所示,图6中t1、t2和t3分别表示管道暴露、管道悬空和冲刷平衡3个不同阶段历时。
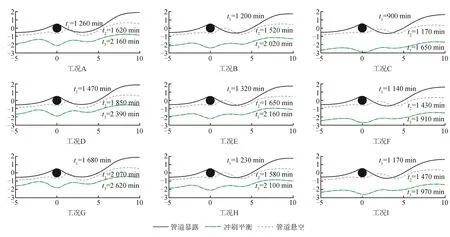
图6 不同工况下河床演变示意图(网格:15 cm×5 cm)
试验观察发现,水下穿越管道附近河床演变规律基本相似,均经历了河床下切、管道暴露、微孔形成、冲坑扩展、管道悬空和冲刷平衡6个阶段,其中试验开始至管道暴露阶段平均历时1 263 min,管道暴露阶段至管道悬空阶段平均历时332 min,管道悬空阶段至冲刷平衡阶段平均历时513 min。对比图6可以发现,在同一流量情况下,流速越大,达到冲刷平衡所需时间越短;在同一流速条件下,水深越浅,达到冲刷平衡用时也越短,工况C达到各阶段的历时最短,工况G达到各阶段的历时最长。其次,对比特征剖面各阶段的河床线发现,各工况下管道暴露阶段的河床线基本一致;但不同工况下管道悬空阶段的河床线出现较大差异,随着流速的增大,河床线起伏逐渐变缓,管道下游局部隆起向下游迁移,同时隆起高度逐渐降低;达到冲刷平衡阶段时,不同工况对应的河床线出现明显差异,同一流量情况下,河床线起伏随着流速的增大逐渐变缓,同一流速条件下,管底最大冲刷深度随水深的减小而增大。
图7为A、B、C工况下达到冲刷平衡时的河床地形图,可以看出,3种工况下管底均出现有局部冲刷现象,管底冲刷是由多个冲坑沿管轴方向逐渐扩展而成,冲坑深度不一,并且管道上游河床高程高于管道下游河床。管道下游河床出现局部隆起,这是由于管底水流剪切应力大于管道下游水流剪切应力,使得管底沙粒被输送至下游后,未能在水流作用下继续向下游运动,在管道下游处出现积累,从而出现河床下游局部隆起。工况A条件下河床地形起伏较大,河床整体下切深度较小,工况B次之,工况C条件下河床地形起伏较缓,河床整体下切深度较大,比较发现,弗劳德数FrA<FrB<FrC,说明水流越急,河床整体下切深度越大,河床地形越平坦。
通过上述对比分析发现,流速和水深共同影响河床各阶段冲刷历时和管底最大冲刷深度,Fr则是反应水流缓急程度的一个无量纲参数,可以同时体现流速和水深共同影响的关系。通过计算公式得知各工况对应的Fr介于0.306~0.808,绘制出最大冲刷深度、达到冲刷平衡历时(T)与Fr之间关系图,如图8所示,其中最大冲刷深度(hm)为冲刷平衡时管道中心距床面的竖向距离。
从图8可以看出,随着Fr增大,hm也随之增大,拟合两者关系得到:hm=2.18Fr+1.2,拟合度R2=0.983,Fr与hm之间呈线性正相关,且hm介于1.3~ 2.4 cm,为管径的0.9~1.6倍;其次,随着Fr的增大,T随之减小,拟合两者关系得到:T=-26 100Fr3+45 620Fr2-26 782Fr+7 267,拟合度R2=0.975,Fr与T之间呈非线性负相关,且T介于1 650~2 620 min。因此,当Fr介于0.306~0.808时,Fr越大,水流越急,导致hm,T越小。
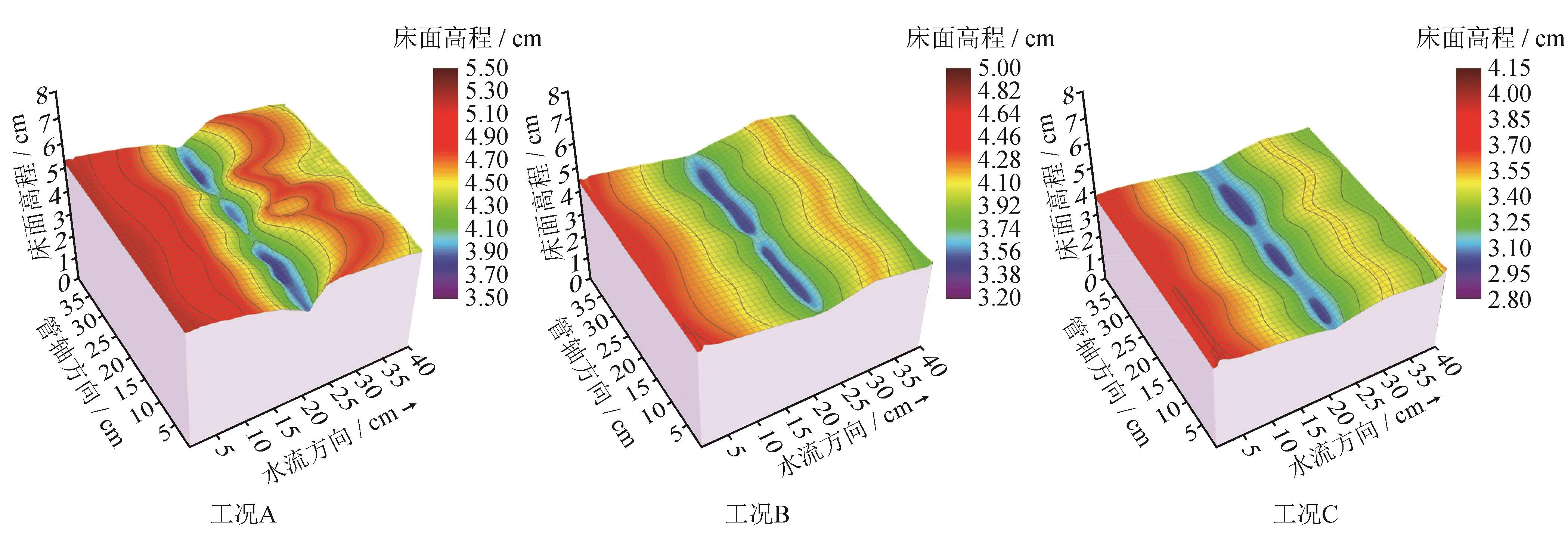
图7 A、B、C工况下冲刷平衡时河床地形图
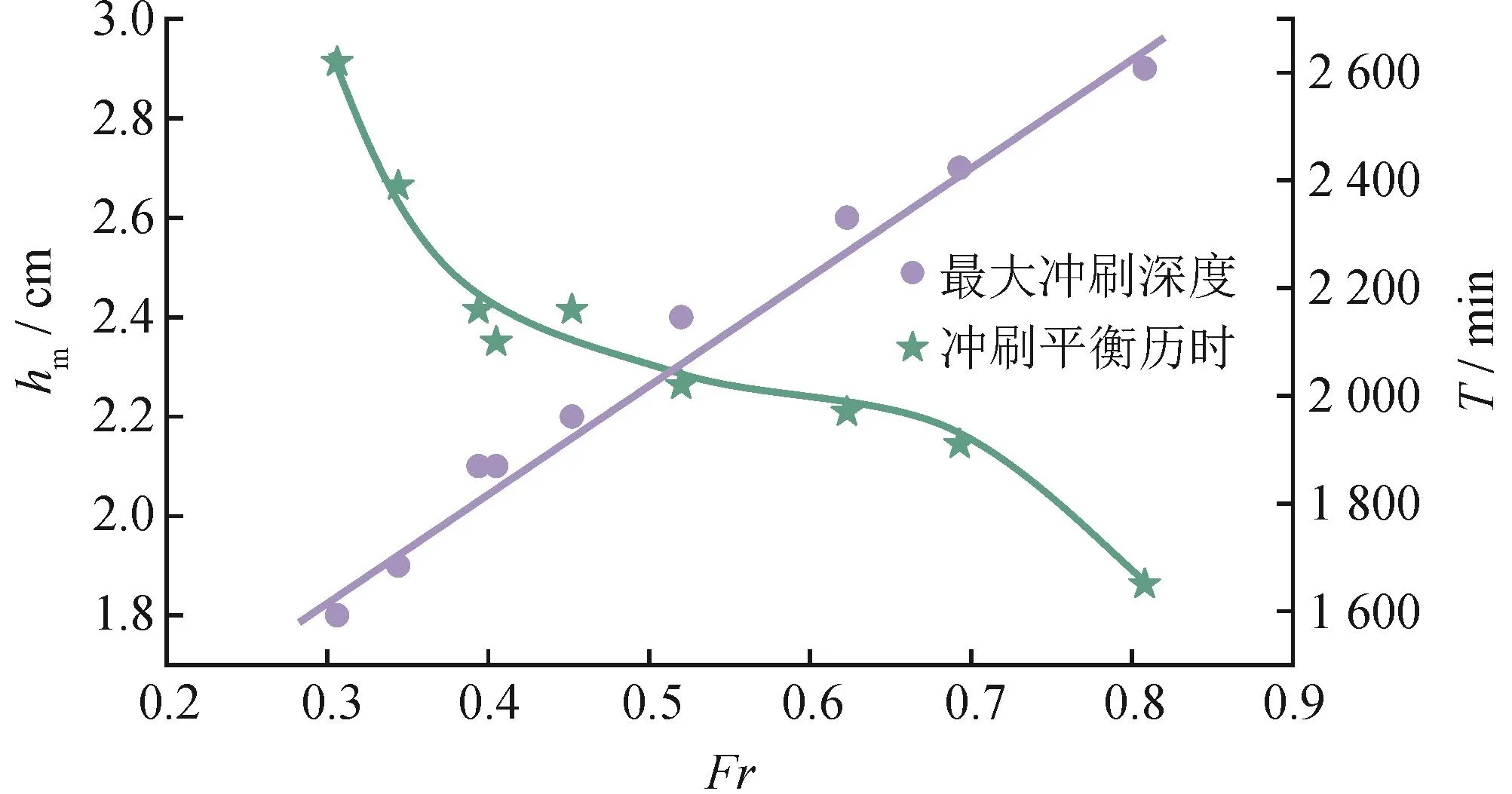
图8 hm、T与Fr之间的关系图
3 结论
1)对于水下穿越管道而言,当水流为缓流时,管道附近河床演变过程可分为:河床下切、管道暴露、微孔形成、冲坑扩展、管道悬空和冲刷平衡6个阶段。
2)导致水下穿越管道产生局部冲刷的原因有涡流和渗流两个方面,管道暴露前涡流使管周沙粒减少,管道暴露后涡流和渗流共同作用使管底出现微孔,从而形成局部冲刷。
3)流速和水深共同影响河床各阶段冲刷历时和管底最大冲刷深度,当弗劳德数介于0.306~0.808时,弗劳德数越大,水流越急,管底最大冲刷深度越大,达到冲刷平衡历时越少,河床整体下切深度越大,河床地形平坦,且管底最大冲刷深度介于1.8~2.9 cm,为管径的0.9~1.6倍,达到冲刷平衡历时介于1 650 ~ 2 620 min。

