等腰三角形解题策略：基本图形++“两头凑”

文陈亚楠

等腰三角形性质与判定是《轴对称图形》这一章的难点，也是常考的知识点。随着几何学习的深入，部分同学出现了面对复杂问题不会分析，面对复杂图形无从下手的情况。有时候题目中并没有直接给出等腰三角形的条件，而是需要大家根据已知推理得到。那么，要构成一个等腰三角形就必须要有相等的边或相等的角。从相等的边来看，根据垂直平分线的性质即可构造等腰三角形（如图1）；从相等的角来看，“平行平分得等腰”是常见的基本图形（如图2）。

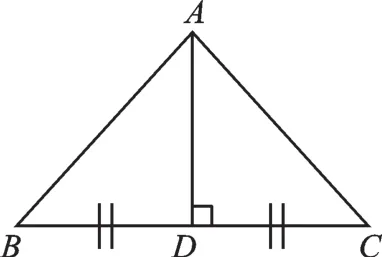
图1

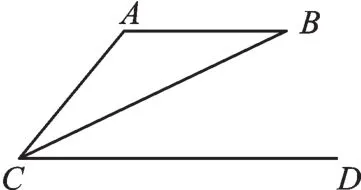
图2

例1如图3，已知在△ABC中，AB=2AC，AD平分∠BAC，AD=BD。求证：CD⊥AC。

【分析】读完题之后我们要思考三方面问题：①已知什么？能得到什么？②求证什么？需要什么？③怎么解决？

首先，由AB=2AC，AD=BD可联想到基本图形图1，取AB的中点E，连接DE，由“三线合一”得DE⊥AB；其次，要证明CD⊥AC，可证明∠ACD=∠AED=90°；最后，由 AD平分∠BAC，证明△AED≌△ACD即可。

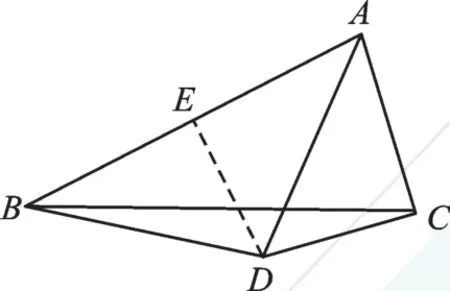
图3

证明：取AB的中点E，连接DE。

∵AD=BD，

∴AB=2AE，DE⊥AB，

∴∠AED=90°。

∵AB=2AC，

∴AE=AC。

∵AD平分∠BAC

∴∠EAD=∠CAD。

在△AED和△ACD中，

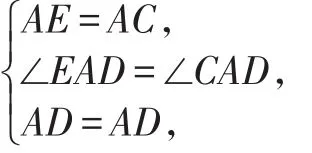
∴△AED≌△ACD。

∴∠ACD=∠AED=90°。

∴CD⊥AC。

例2如图4，在△ABC中，∠ABC、∠ACB的平分线相交于点O，MN过点O，与AB、AC相交于点M、N，且MN∥BC，求证：△AMN的周长等于AB+AC。

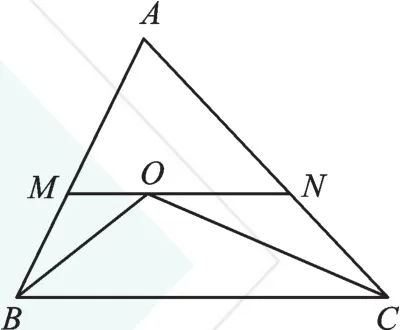
图4

【分析】首先，已知平行、平分，由基本图形图2可得△BMO和△CNO是等腰三角形；其次，求证C△AMN=AB+AC，需证MN=MB+NC；最后，由腰相等进行等量代换即可。

证明：∵BO平分∠ABC，

∴∠ABO=∠CBO。

∵MN∥BC，

∴∠MOB=∠CBO，

∴∠ABO=∠MOB，

∴BM=MO。

同理，CN=NO。

∴C△AMN=AM+MN+AN=AM+MO+NO+AN=AM+MB+NC+AN=AB+AC。

以上两道例题涉及了之前提到的两个基本图形，它能够帮助我们快速地将复杂图形分解成熟悉的简单图形。当然，基本图形也不能帮助我们完全解决复杂几何题，还需要我们学会分析问题。在上面两道题的分析中，陈老师要同学们思考三个方面的问题：①已知什么？能得到什么？②求证什么？需要什么？③怎么解决？其实这就是结合条件和所要证明的结论一起考虑，即“两头凑”，做到这些，遇到新题就不会束手无策了。