基于BDS精密星历产品的水汽探测性能分析

吴旭祥,郭秋英,侯建辉

(山东建筑大学 测绘地理信息学院，山东 济南 250101)

0 引 言

水汽是大气的重要组成部分,在天气及气候变化中起重要作用,在气象学中通常以大气可降水量(PWV)来表示空气柱中的水汽总量,其值反映了大气中水汽含量的丰富程度.实时获取PWV对于中小尺度天气预报、气象学研究等有重要意义.

近年来,随着我国北斗卫星导航系统(BDS)的发展和完善,国内外众多学者开始结合气象学领域对BDS的水汽探测性能进行评估分析,基于地基BDS的大气水汽探测技术也初步应用于气象监测、数值天气预报等领域,实现对大气水汽的低成本、全天候、稳定和实时监测,为改善中小尺度数值天气预报和气象学研究提供重要的、较为理想的大气水汽观测数据,具有良好的应用和发展前景[1].

本文基于全球卫星导航系统(GNSS)双差定位技术,利用多模GNSS实验项目(MGEX)和单基站连续运行参考站(CORS)提供的多星座观测数据, 采用武汉大学发布的BDS最终精密星历产品(WUM)、快速精密星历产品(WHR)和超快速精密星历产品(WHU),利用GAMIT软件解算获得大气水汽结果,分别与IGS对流层延迟产品、GPS水汽探测结果、欧洲中期气象预报中心(ECMWF)的ERA-5再分析资料产品和美国怀俄明州立大学(UW)提供的探空站数据进行对比,分析验证当前三种星历产品应用于BDS卫星水汽探测的精度及可靠性,为进一步提高BDS卫星的水汽探测性能提供一定的参考.

1 地基GNSS水汽探测原理

卫星信号在中性大气层传播时受大气成分的影响,其传播速度减慢,传播路径发生弯曲,从而产生信号延迟,称为对流层延迟[2].处理对流层延迟通常是将斜路径方向的对流层延迟转化到天顶方向上,其公式表示为

ZTD=ZHD+ZWD，

(1)

式中:ZTD为与卫星仰角θ有关的对流层总延迟量;ZHD为对流层天顶静力延迟,也称为对流层天顶干延迟;ZWD为对流层天顶湿延迟.

干燥空气引起的ZHD较为稳定,存在一定规律性,可以通过萨斯塔莫宁(Saastamoinen)模型[3]、霍普菲尔德(Hopfield)模型[4]等较好地推算得到,本文选择萨斯塔莫宁模型计算静力学延迟,即

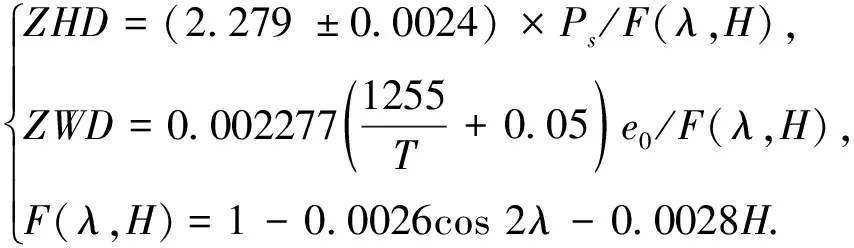
(2)

式中:Ps为测站地表气压，hPa;e0为水汽压，mbar;T为温度，K;λ为测站地理纬度;H为测站大地高，km.

水汽的时空变化较为剧烈,ZWD通过数学模型计算会产生cm级误差[5].因此一般不用模型表达ZWD,而是从ZTD中减去ZHD得到ZWD.PWV与ZWD存在以下比例关系:

PWV=Π×ZWD,

(3)

式中,Π为与对流层温度有关的转换系数,有

(4)

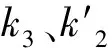
2 数据处理及分析

2.1 数据来源

2011年起国际GNSS服务中心(IGS)开展了跟踪、收集和分析全球可用的GNSS信号的MGEX项目,对外提供多模GNSS观测数据和星历等产品[8].

本次实验利用单基站CORS和MGEX站2018年年积日120～150 d共31天的观测数据,其测站分布位置如图1所示.其中,山东建筑大学卫星导航定位实验室提供单基站CORS多模观测数据,测站点名标记为JZDX.亚太地区选取8个提供多模观测数据的MGEX测站,测站点名分别是BRUN、CMUM、GMSD、HKWS、JFNG、KARR、KIRI、MCHL.以上观测数据均包含BDS和GPS观测量,采样间隔为30 s.

图1 测站分布图

武汉大学针对BDS发布了三种不同时效性需求的BDS星历轨道产品,分别为WUM、WHR、WHU.其中WUM、WHR常用于事后数据处理,WHU常用于实时性数据处理.

2.2 数据分析

为分析BDS卫星水汽探测的性能,评价BDS反演PWV的外符合精度,将基于三种BDS精密星历解算的BDS/PWV分别与IGS对流层延迟产品、GPS水汽探测结果、ERA-5再分析资料产品和探空站数据进行对比.

2.2.1 BDS反演ZTD精度分析

ZTD是反演大气水汽含量的重要影响因素,其精度在很大程度上影响到PWV的解算精度,IGS提供采样间隔5 min,精度优于4 mm的对流层天顶延迟产品,该产品具有较高的精度和可靠性,可以作为评定大气水汽解算精度和可靠性的外符合手段之一[9].

本次实验获取到GMSD、HKWS、JFNG、KARR、KIRI和MCHL共6个测站的IGS对流层天顶延迟产品.上述6个测站的BDSZTD解算值和GPS基于最终精密星历(IGF)解算的ZTD与对应的IGS对流层天顶延迟产品的RMS统计情况如图2所示,由于篇幅原因限制,图3示出了只取HKWS站BDS/ZTD和IGS/ZTD的时间序列.

图2 BDS、GPS的ZTD解算值与IGS/ZTD偏差的RMS

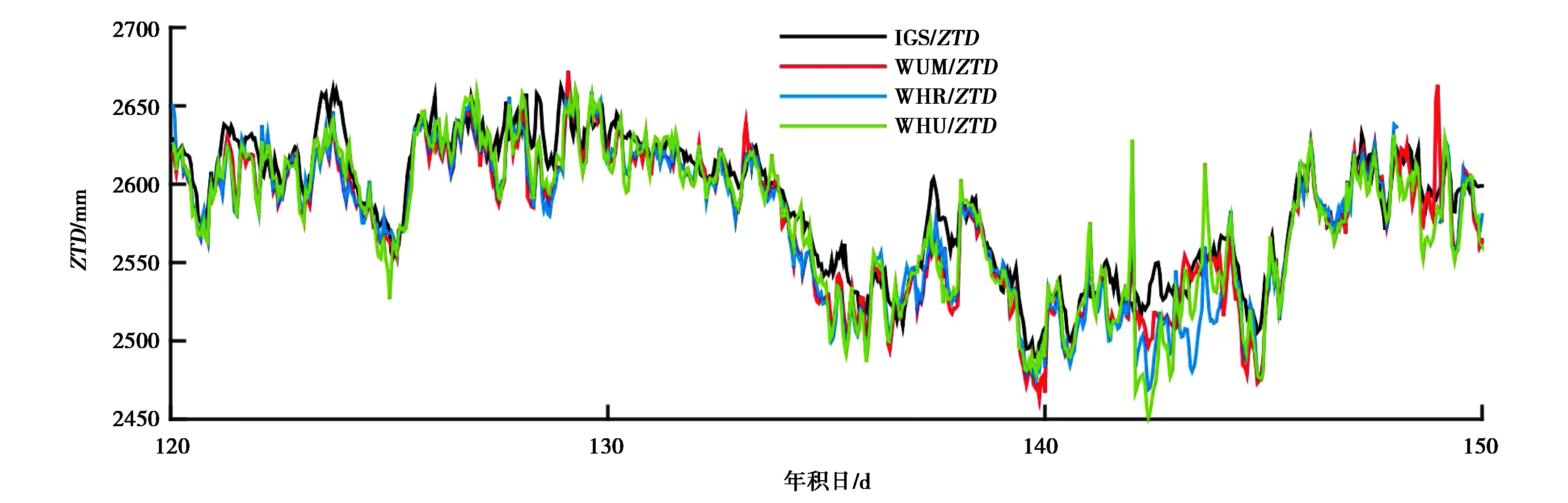
图3 HKWS站ZTD时间序列

从图2～3看出,三种BDS星历中WUM解算ZTD的精度最高,WHR解算ZTD的精度次之,WHU解算ZTD精度稍逊于前两者.BDS整体与GPS基于IGF解算的ZTD相比存在1 ～2 cm左右的差异,BDS解算ZTD的变化趋势较为一致,但精度要低于GPS.

表1示出了根据三种BDS星历产品进行分类,统计BDS/ZTD与IGS对流层天顶延迟产品的数值差异情况.从表1可以看出,三种BDS星历的ZTD解算值分别有4464、4326和4464个,与IGS/ZTD的平均偏差(Bias)均大于7 mm,标准差(Std)大于22.09 mm,均方根值(RMS)大于23.37 mm.结合图3可以发现BDS解算ZTD的结果中存在较多的异常值,考虑到粗差影响,在将大于三倍中误差的数值剔除掉后, BDS/ZTD与IGS/ZTD的Std大于19.80 mm,RMS大于21.15 mm.

表1 BDS/ZTD与IGS/ZTD的差异统计

获取可用的、高精度的大气水汽含量的重要因素是卫星的轨道精度,段晓梅等[9-10]研究发现对于1000 km的长基线,10 cm的卫星轨道误差会引起1.3 mm的ZWD误差,0.2 mm的PWV误差.通过了解BDS卫星的轨道设计可知,BDS按轨道有地球静止轨道卫星(GEO)、倾斜同步轨道卫星(IGSO)和中圆轨道卫星(MEO)三种卫星共同组成空间部分.但GEO卫星分布的几何结构较差,轨道、钟差和模糊度等参数相关性较高,定轨法方程呈病态,导致GEO卫星切向存在1～4 m的常偏量误差[11],轨道误差远高于IGSO和MEO卫星.

考虑到参与解算的观测站均位于亚太地区,BDS卫星观测条件较好,测站每日可观测BDS卫星的总数在12颗左右,每日可观测IGSO和MEO卫星总数在8颗左右.张婧宇[12]等通过实验发现对可见BDS卫星数大于8颗的测站而言,解算的ZTD具有与GPS/ZTD相当的精度.因此在BDS卫星观测条件较好的区域,解算策略上采取只使用轨道精度较高的IGSO和MEO卫星的方法,在一定程度上能提高BDS水汽反演精度.

图4 HKWS站ZTD时间序列(不含GEO卫星)

图5 BDS、GPS的ZTD解算值与IGS/ZTD偏差的RMS(不含GEO卫星)

采取只使用IGSO和MEO卫星的解算策略后重新解算ZTD,HKWS站BDS/ZTD与IGS/ZTD时间序列如图4所示,两者吻合程度与一致性较之前明显提高,异常值数量较图3有明显减少.图5示出了6个测站ZTD的RMS统计情况，可以看出各测站的RMS数值较图2有明显的减小.表2示出了BDS/ZTD与IGS/ZTD的数值差异情况再次分类统计,BDS/ZTD与IGS/ZTD的偏差降低到5 mm左右,Std小于17.01 mm,RMS小于17.84 mm.在剔除三倍中误差后,Std最小为11.95 mm,RMS最小为13.16 mm.BDS/ZTD与IGS/ZTD的相关系数均高于0.99,表现为正相关且强相关.WUM、WHR和WHU解算ZTD的RMS分别为13.16 mm、13.21 mm和16.40 mm,较之前分别减小37.8 %、42.7 %和33.9 %,整体精度与使用GEO卫星解算ZTD相比有明显提高.因此在后续的实验中也采取只使用IGSO和MEO卫星的解算策略进行解算.

表2 BDS/ZTD与IGS/ZTD的差异统计(不含GEO卫星)

2.2.2 BDS/PWV与GPS/PWV对比分析

1993年Rocken[13]等通过GPS/SRTOM实验,将GPS解算的PWV与水汽辐射计结果进行对比,结果显示两者偏差小于0.5 mm,RMS达到1.5 mm,验证了GPS反演PWV的精度.为评价BDS使用三种星历产品反演PWV的外符合精度,将三种BDS星历产品解算的PWV与GPS使用IGF解算的PWV进行对比分析.篇幅限制原因,图6示出了HKWS站应用三种BDS星历解算的PWV与IGF/PWV的数值差异情况.图7示出了9个测站使用三种BDS星历解算的PWV与IGF/PWV的整体相关性拟合情况.从图6、图7可以看出三种BDS星历产品的解算PWV与IGF/PWV相比,BDS与GPS的整体偏差在5 mm以内,稳定性较好.R2大于0.97,表现为较高的拟合优度.P值为0,表示差异具有高度统计意义.

(a)WUM (b)WHR (c)WHU

(a)WUM (b)WHR (c)WHU

表3示出了BDS/PWV与IGF/PWV之间的差异统计,从表3可以看出:BDS/PWV与IGF/PWV的偏差在0.7 mm左右,Std小于2.76 mm,RMS小于2.81 mm,在剔除掉大于三倍中误差的数值之后Std小于2.50 mm,RMS小于2.61 mm.BDS/PWV与IGF/PWV相关系数高于0.98,表现为强相关性.综上可以认为,BDS与GPS吻合程度较高,具有很好的一致性.

表3 BDS/PWV与IGF/PWV的差异统计

2.2.3 BDS/PWV与ERA-5/PWV对比分析

ECMWF是国际上权威的天气预报研究和业务机构,对外发布高精度的再分析模式和预报产品.ERA-5是ECMWF发布的第5代全球气候再分析资料产品,ERA-5提供分析场水平分辨率为31 km的逐小时格点气候数据记录[14],通过与测站点相邻的4个格网点到测站的距离,采用双线性内插的方法得到对应测站点的PWV时间序列(ERA-5/PWV).

图8示出了9个测站BDS、GPS解算的PWV和对应的ERA-5/PWV数值差异的RMS统计情况，可以看出三种北斗星历解算的PWV与ERA-5/PWV相比，RMS在3 mm左右，WUM星历整体的精度要高于WHR和WHU，稍低于GPS.图9示出HKWS站BDS/PWV和ERA-5/PWV的数值序列，序列表现出较高的一致性，无明显系统性偏差.

图8 PWV解算值与ERA-5/PWV偏差的RMS

图9 HKWS站PWV时间序列

将BDS/PWV按星历进行分类后与ERA-5比较得到表4所示结果,三种星历的PWV解算值与ERA-5/PWV的偏差在0.3 mm左右,Std小于3.94 mm,RMS小于3.91 mm,在剔除掉大于三倍中误差的数值之后Std小于3.74 mm,RMS小于3.74 mm.WUM、WHR和WHU三种星历解算PWV的RMS分别为3.44 mm、3.47 mm和3.74 mm,WUM精度优于WHR和WHU.三种星历解算的PWV与ERA-5/PWV相比较, 相关系数均高于0.97,相关性较强.

图10示出了9个测站基于BDS三种星历解算的PWV与ERA-5/PWV的整体相关性拟合情况,从图10可以看出三种BDS星历产品的解算PWV与ERA-5/PWV相比,R2均在0.95以上,与ERA-5再分析资料拟合程度较高,稳定性较好,具有较高的可靠性.P值均为0,差异具有高度统计意义.

表4 BDS/PWV与ERA-5/PWV的差异统计

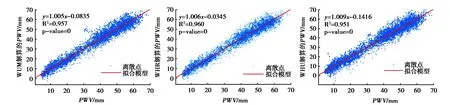
(a)WUM (b)WHR (c)WHU

2.2.4 BDS/PWV与无线电探空数据对比分析

无线电探空法(RS)是目前公认较为可靠的PWV测量方法之一,通过探空气球携带无线电探空仪的方式采集气球上升路径各个高度的温度、气压、湿度等实测数据.无线电探空仪计算的PWV精度在mm级,逐12 h记录,可以作为独立验证BDS探测水汽精度的外部基准.通过美国怀俄明州立大学网站(http://weather.uwyo.edu/upperair/sounding.html)下载相关测站的无线电探空站数据.

以HKWS站为例，将BDS/PWV解算值与RS/PWV探测值进行比较,PWV时间序列及所有测站的回归分析分别如图11、图12所示.从中可以看出HKWS站的BDS/PWV解算值与RS/PWV一致性较高,变化趋势较为一致,无明显系统性偏差.WUM、WHR和WHU星历产品解算的PWV与RS/PWV相比,R2均大于0.91,整体拟合优度较高.P值为0,差异具有高度统计意义.

图11 HKWS站BDS/PWV与RS/PWV时间序列

(a)WUM (b)WHR (c)WHU

表5示出了WUM、WHR和WHU三种BDS星历解算的PWV与RS/PWV的差异统计情况.总体来说,BDS解算的PWV与RS/PWV相比,偏差在1 mm左右,RMS优于5 mm,相关系数在0.9以上,两者表现为正相关且强相关,整体趋势性较好.考虑到探空数据逐12 h记录一次,观测时间分辨率较低,样本总数量相对有限,少量偶然误差对整体精度产生较大的影响,通过BDS/PWV与RS/PWV的检核,可以认为BDS卫星水汽探测较好地反映了实际的PWV变化情况,与探空数据实测值并无明显的系统性偏差,可靠性较强,满足地基GNSS反演PWV相对精度限值5 mm的要求[15],可以用于数值天气预报等应用要求.

表5 BDS/PWV与RS/PWV差值分析统计

3 结束语

本文利用武汉大学发布的WUM、WHR和WHU BDS星历产品,采用MGEX和单基站CORS提供的BDS/GPS多星座观测数据,借助GAMIT软件对BDS水汽探测能力的精度和可靠性进行分析,主要得出以下结论:

1)高精度的卫星轨道是保证水汽反演精度的关键,在BDS卫星可观测数目较多的区域,采取只使用轨道精度较高的IGSO和MEO卫星的解算策略,应用三种星历产品解算ZTD的Std平均在12 mm,较使用GEO、IGSO和MEO三种卫星的解算策略解算ZTD的精度提高33.9%左右,一定程度上提高了BDS水汽探测精度,可以认为BDS的ZTD解算精度与IGS对流层延迟产品基本相当.

2)对比分析了BDS、GPS在大气水汽反演中的性能,与GPS相比,基于BDS WUM、WHR和WHU星历产品反演PWV的精度分别为2.11 mm、2.14 mm和2.61 mm,与GPS解算的PWV的相关系数均高于0.98,验证了BDS三种星历产品反演PWV的精度和可靠性,可以认为BDS卫星水汽探测的精度与GPS相当.

3)在BDS与ERA-5、RS的大气水汽结果的对比分析中,应用BDS WUM、WHR和WHU星历产品解算的PWV与ERA-5/PWV的RMS分别为3.44 mm、3.47 mm和3.74 mm,与RS/PWV的RMS为4.39 mm、5.32 mm和4.69 mm,相关系数均高于0.9,无明显系统性偏差,验证了BDS反演PWV的外符合精度与可靠性,相对精度满足中小尺度数值天气预报和气象学研究等要求.