顾及有色噪声的ETS对GPS坐标时间序列影响分析

王子舆,李仲勤

(1.兰州交通大学 测绘与地理信息学院,甘肃 兰州 730070；2.甘肃省地理国情监测工程实验室,甘肃 兰州 730070)

0 引 言

有学者研究表明较长的国际GNSS服务(IGS)坐标时间序列中存在慢滑移(ETS)现象[1-2].在日本与卡斯卡迪亚地区及澳大利亚地区均有板块构造边界处ETS现象的发生[3-4],研究表明GPS坐标时间序列中,有假设闪烁噪声+白噪声(FN+WN)与幂律过程同时估计谱指数的方式对线性的构造信号具有等效性[5].文献[6]研究指出基于WN假设得到的速度估计存在较大的偏差且速度不确定度被过高估计;而在文献[7]中研究表明在美国南加州等地的GPS站坐标时间序列中包含有高斯-马尔科夫噪声(GGM)和带通滤波噪声.考虑ETS存在的特殊性,选择合适的组合有色噪声模型及较长GPS坐标时间序列,有必要进一步研究ETS对GPS站坐标时间序列的影响.

为此,本文以全球范围内12个GPS站10年的坐标时间序列为研究对象,采用基于Fisher信息矩阵的Kashyap信息准则 (KIC),选取FN+WN、幂律噪声+白噪声(PL+WN)、高斯-马尔科夫噪声+白噪声(GGM+WN)、闪烁噪声+随机游走噪声+白噪声(FN+RW+WN)四种组合噪声模型,并探讨ETS对GPS站时间序列的影响.

1 噪声模型估计准则

BOS[8-9]提出基于Akaike信息准则/Bayesian信息准则(AIC/BIC)噪声模型的估计方法,克服了极大似然估计(MLE)值越大偏差越大的缺陷,但Kashyap[10]的研究表明AIC噪声模型估计准则的严密性不够,指出AIC会过高的评价真实的模型.文献[11]研究证实了AIC/BIC方法的优越性,但也存在一定的发散性.当AIC/BIC不一致时,如何确定噪声模型,有待进一步研究.为了进一步提高噪声模型估计的稳健性,本文提出在BIC的基础上引入基于Fisher信息矩阵的Kashyap信息准则(KIC),其原理为[12]

KIC=BIC+Indet(I),

(1)

式中,I为Fisher信息矩阵,I的值受随机模型的影响.Fisher信息矩阵反映对MLE参数估计的准确度,Fisher信息量越大,对参数估计的准确度越高.

2 噪声模型对IGS站速度及其不确定度影响分析

2.1 GPS站速度数学模型

目前国内外许多学者探讨分析噪声模型对IGS站速度及其不确定度的影响,KLOS、BOS等人[9,13]对GPS站速度进行线性回归法拟合,噪声模型对站速度的准确估计可表示为

mv≈

(2)

式中:N为观测值时间序列长度;κ代表估计谱指数;ΔT为采样率;APL为噪声振幅;τ为伽玛函数.

2.2 噪声模型影响分析

探讨ETS对噪声模型影响分析,分别对所选择的四种噪声模型进行ETS前后噪声模型估计,以慢滑移参数为130天,分析ETS前后GPS站噪声模型变化,图1示出了E、N、U方向对应ETS前后四种噪声模型所占比例.

图1 ETS前后各噪声模型占比

由图1可知,E分量ETS前无FN+WN及GGM+WN噪声模型,91.7%的GPS站表现为FN+RW+WN,8.3%的GPS站表现为PL+WN噪声模型,ETS后无PL+WN及GGM+WN噪声模型,FN+WN与FN+RW+WN噪声模型各占比50%.说明在经ETS后,部分站的噪声模型发生了改变,由ETS引起测站模型选择的PL+WN噪声模型改变为FN+WN噪声模型,引起模型的错误估计.N分量ETS前后噪声模型的类型无变化,ETS前表现为FN+WN与FN+RW+WN,各占比50%,ETS后FN+WN噪声模型占比83.3%,16.7%的GPS站表现为FN+RW+WN噪声模型,说明ETS前RW的影响占比较大.U分量ETS前GPS站主要表现为GGM+WN噪声模型,占比为50%,FN+WN与PL+WN噪声模型各占比25%,ETS后GGM+WN噪声模型占比增加至66.6%,FN+WN与PL+WN噪声模型均减少至16.7%,但均无FN+RW+WN噪声模型.综上可得,ETS导致GPS站坐标序列模型发生变化,在E分量与N分量影响较大,且ETS可能造成噪声模型的错误估计.

2.3 ETS对IGS站速度影响分析

进一步探讨ETS对GPS站速度变化规律,以ETS参数为130天,对E、N、U三分量ETS前后站速度进行对比分析,如图2所示.

图2 ETS前后速度值对比

由图2可知,E分量ETS前后各噪声模型站速度值变化曲线规律类似,其中P418站、PABH站及PGC5站速度值较大,最大值达14.87 mm/a,LKCP站ETS前后站速度值无变化.N分量ETS前后站速度曲线与E分量类似,变化差异较大的为PABH站,站速度最大值为11.31 mm/a,其中DDSN站、P418站速度略大,分别为7.45 mm/a、6.03 mm/a,经SOPAC观测资料显示,站速度发生较大变化可能的原因是DDSN站与P418站的E分量上于2010年分别发生了约-6.74 mm/a与8.05 mm/a的同震位移,而PABH站的U分量分别于2002年、2011年发生6.30 mm/a、7.74 mm/a的形变.U分量上,各噪声模型ETS前后各噪声模型站速度值变化较小,90%的站滤波前后站速度不大于5 mm/a,KTBW站与P418站ETS前后站速度差值较大.统计N、E、U三分量不同噪声模型下ETS站速度差值极值,如表1所示.

表1 慢滑移前后站速度差值极值(绝对值)mm

极值类型EFN+WNPL+WNGGM+WNFN+RW+WNNFN+WNPL+WNGGM+WNFN+RW+WNUFN+WNPL+WNGGM+WNFN+RW+WN 最小值00.100.28000.030.1000.010.070.050 最大值4.154.134.154.072.562.512.182.574.674.625.154.67 均值2.162.392.072.691.091.110.981.131.451.381.421.45

由表1可知,E分量上ETS前后FN+WN与FN+RW+WN噪声模型站速度差值最小值为0,GGM+WN噪声模型站速度差值最大为4.15 mm/a,但ETS前后各噪声模型站速度差值均值略大,在0～2.7 mm/a之间.N分量上,PL+WN与GGM+WN噪声模型站速度差值最小值为0.03 mm/a、0.1 mm/a,FN+WN噪声模型站速度差值最大为2.56 mm/a,ETS前后各噪声模型均值约为1.0 mm/a.U分量PL+WN噪声模型站速度差值最小值比其他噪声模型站速度略大,约为0.07 mm/a,其中,FN+WN噪声模型站速度差值最大值较大，为4.67 mm/a,但各噪声模型站速度差值均值不超过1.5 mm/a.综上可得,ETS前后U分量站速度变化比E分量、N分量明显,但在E分量上GPS站ETS速度相对较大.

2.4 ETS参数对噪声模型影响分析

以ETS参数为130天的分析表明,GPS站速度在E分量上影响较为明显.探讨分析ETS参数的影响,将ETS参数为100天与130天的站速度变化规律进行对比分析,E、N、U分量上不同站速度对比如图3所示.

图3 两参数站速度对比

由图3可知,E分量上58%的GPS站速度变化值较小,NANO站、P439站、PGC5站、SC04站与SEAT站速度变化稍大,可能的原因是,NANO站SC04站与SEAT站的N分量、U分量分别于2003年、2001年发生6.145 mm/a、9.401 mm/a的同震形变,引起较大的站速度变化.N分量约92%的GPS站速度估计趋于稳定,仅有1站站速度估计偏大.U分量上约83.3%的GPS站速度变化趋近于0,站速度较大的2站为DDSN站与SEAT站.SOPAC的观测日志资料显示SEAT站分别于1998年、2001年、2011年发生了约9～12 mm的位移,同样DDSN站于2008年、2011年均发生了不同程度的同震形变.综上表明,ETS参数从100天增加至130天,约60%的GPS站速度估计值趋于稳健,但受地震运动影响的GPS站速度变化较大.

2.5 ETS对IGS站速度不确定度影响分析

探讨ETS对站速度不确定度的影响分析,如图4所示为ETS前后站速度不确定度值变化规律曲线.

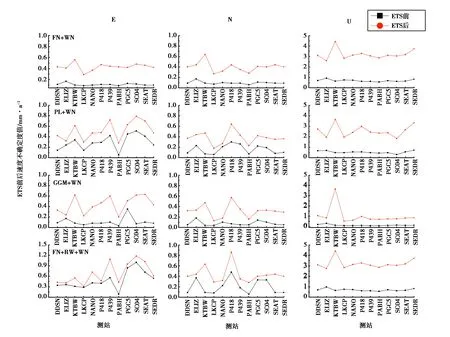
图4 ETS前后站速度不确定度值变化规律

由图4可知,E分量FN+WN噪声模型ETS前后站速度不确定度曲线变化较小,但ETS前后差值略大,FN+WN、PL+WN、GGM+WN及FN+RW+WN噪声模型ETS后站速度不确定度大于ETS前站速度不确定度,其中BAPH站ETS前站速度不确定度约为0;GPS站如P439、KTBW、SC04、SEAT等站纠正前后站速度不确定度变化明显;N分量FN+WN、GGM+WN噪声模型ETS前站速度不确定度变化在0上下波动,FN+WN与FN+RW+WN噪声模型ETS前比ETS后站速度不确定度稳定且较小,其中KTBW、P418站速度不确定度ETS后比ETS前增大, 出现这种变化可能的原因是两站于2011年U分量发生了较大位移,且两站的站速度ETS前后变化也较大;U分量上各噪声模型站速度不确定度在0～1之间变化且稳定,但KTBW站站速度不确定度值较大,同震形变引起了站速度的过高估计,ETS后的站速度不确定度比ETS前站速度不确定度均大.综上所述可知,U分量上ETS对站不确定度影响较大,在准确估计站速度不确定度时必须考虑ETS的影响,否则可能导致过高估计站速度不确定度.统计ETS前后站速度不确定度差值,如表2所示.

表2 ETS前后测站速度不确定度差值(绝对值)极值mm

极值类型EFN+WNPL+WNGGM+WNFN+RW+WNNFN+WNPL+WNGGM+WNFN+RW+WNUFN+WNPL+WNGGM+WNFN+RW+WN 最小值0.2090.0840.0680.0270.2000.1230.0860.0371.6531.2530.4351.759 最大值0.4620.3040.5450.5300.5420.4000.5060.5403.7733.1551.5203.773 均值0.3220.2260.3310.1940.3030.2200.2340.2362.4962.0250.7232.503

由表2可知,E分量ETS前后站速度不确定度差值较小,最大差值约为0.5 mm,ETS前后站速度不确定度差值最小约为0.027 mm;N分量与E分量站速度不确定度差值变化情况一致;U分量站速度不确定度差值变化较大,FN+WN与FN+RW+WN噪声模型ETS后站速度不确定度差值比N、E分量站速度不确定度差值最大值均大,最小差值分别约为1.653 mm、1.759 mm,最大差值均为3.773 mm.综上可知,ETS对站速度不确定度在U分量影响较为明显.

3 结束语

本文选取12个GPS站坐标时间序列,基于Fisher信息矩阵的KIC噪声模型估计准则对噪声模型选取的可靠性进行评估,以ETS参数为130天为例,探讨ETS对GPS站时间序列的影响,结果表明:

1)在E分量与N分量上,ETS对FN+RW+W噪声模型影响较大(分别占比91.7%、50%),ETS导致GPS站坐标序列模型发生变化且ETS可能造成噪声模型的错误估计.此外,选取较多有色噪声模型或更多GPS站时的占比变化,需进一步研究.

2)ETS前后U分量站速度变化比E分量、N分量明显,但在E分量上GPS站ETS速度相对较大.ETS参数从100天增加至130天,约60%的GPS站速度估计值趋于稳健,但受地震运动影响的GPS站速度变化较大,对GPS时间序列进行噪声模型估计时,可将地震带的测站可进行标记研究,尽量减少地震运动带来的不利影响.

3)特殊地理位置的GPS测站(如SEAT、KTBW站),ETS前后站速度及站速度不确定度变化较大,且在U分量表现较为明显,ETS后的站速度不确定度比纠正前站速度不确定度均大,因此在准确估计站速度及站速度不确定度时,必须考虑ETS带来的影响.