抗差估计在RTK/INS紧组合中的应用研究

储超,黄亮,杜仲进,叶世榕

(1.武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079;2.中国民航科学技术研究院法规标准研究所,北京 100028;3.福建省测绘院,福州 福建 350003)

0 引 言

全球卫星导航系统(GNSS)定位技术是室外车载导航的重要手段,但在卫星信号缺失或遮挡严重环境下会导致GNSS无法进行有效导航,融合惯性导航系统(INS)可有效解决上述问题,因此GNSS/INS组合导航定位技术是导航领域的研究热点.GNSS/INS组合导航包括松组合和紧组合,紧组合可有效利用原始信息辅助GNSS整周模糊度的固定,具有更突出的优势.Grejner-Brzezinska[1]利用INS预测结果和候选位置的分离,排除了部分候选,缩短了动态GNSS模糊度搜索时间.Scherzinger[2]提出,在INS辅助载波相位差分(RTK)中,整数模糊度恢复时间为1～4 s,而在标准RTK中,在完全中断长达60 s之后,模糊度恢复时间为10～15 s.刘帅[3]和朱锋[4]均提出了PPP/INS紧组合的算法实现,证明该算法的可行性及提高模糊度固定率;李团[5]分析了城市环境下BDS/GPS双系统RTK/INS紧组合的性能,证明该算法提高了城市环境下GNSS动态精密定位的可用性和精度;上述文献均没有分析对粗差的影响.

GNSS/INS组合仍不能避免粗差等异常信号对其定位的影响.何秀凤等[6]提出了GPS/INS组合导航系统抗差滤波器的设计方法,表明对不确定的噪声方差,抗差极小极大滤波器比常规滤波器有更好的性能.吴富梅等[7]提出了基于部分状态不符值构造的自适应因子应用于GPS/INS紧组合导航,但是该算法未利用到载波相位观测值.高为广等[8]提出了IMU/GPS组合导航系统自适应Kalman滤波算法,证明自适应Kalman滤波算法能同时抑制状态估计误差和状态扰动误差的影响.韩厚增[9]提出了基于最小二乘的惯导辅助BDS/GPS抗差自适应模糊度固定方法,可以减小观测值粗差对于模糊度解算的影响.

上述算法均考虑了伪距粗差,但是对因相位观测值所产生的误差并未加以考虑,而相位粗差可能会导致模糊度估计错误,导致出现定位粗差,本文打算综合考虑伪距和相位粗差,以降低两者对于定位稳定性的影响.但是以上方法并未对RTK/INS紧组合中载波相位观测值的新息进行抗差处理,基于此,本文提出了一种基于伪距和相位的新息抗差卡尔曼滤波的GPS/BDS双系统RTK/INS紧组合导航定位算法,并用实验验证此方法是否也能提升定位精度.

1 RTK/INS紧组合算法

在捷联惯性导航中,惯性测量单元(加速度计和陀螺仪)直接与运载体固联.陀螺和加速度计分别用于测量运载体的角运动和线运动.可以依据惯导的机械编排求解更新惯导系统的姿态、速度和位置等导航参数.由于惯导的机械编排结果会随着时间的增加而快速发散,产生了惯导与卫导的组合导航模式,为了与GNSS数据融合,本文INS机械编排以及滤波均采用的是ECEF(Earth-Centered Earth-Fixed Coordinate System)坐标系,简称E系,而非传统的北东地或者东北天坐标系.

1.1 地心地固坐标系下的系统方程

为了实现RTK/INS紧组合必须建立相应的误差状态模型,首先需要建立惯性导航系统在ECEF坐标系(E系)下的误差状态模型.建模如下:

XINS=

(1)

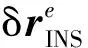
(2)

xk+1=Φ(k+1)/kxk+wk.

(3)

其中,一般假设在Δt时间内变化不太剧烈,且F(tk)Δt远小于单位阵I,则有

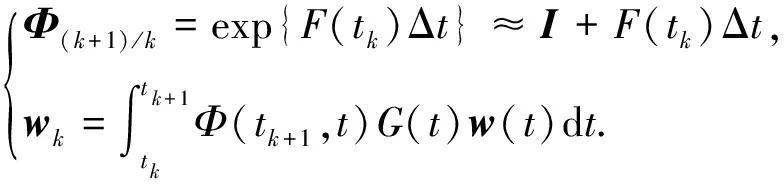
(4)

因为紧组合直接利用GNSS的原始观测信息,因而在进一步预测的时候,需要对模糊度参数和INS误差状态量参数一起进行时间更新[4].本文介绍的是短基线情况,故对流层和电离层等参数均不参与滤波,仅包含模糊度.整体的F阵表述如下:

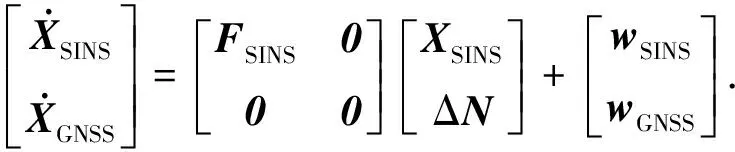
(5)

1.2 ECEF系下的捷联惯导观测模型

在组合导航中,由于IMU中心和GNSS天线中心不重合,在构造观测方程的时候需要考虑杆臂误差.经杆臂改正可得GNSS天线相位中心在真值处的扰动量[4]为

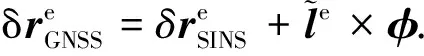
(6)

进一步结合式(3)和(4)可得RTK/INS观测方程:

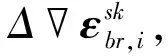
(7)

(8)

1.3 模糊度解算和闭环修正

将紧组合Kalman滤波估计得到的模糊度浮点解及其方差协方差阵,代入Lambda函数进行模糊度固定.将估计的位置、速度、姿态误差用来修正惯导推算的结果,逐步得到一个更加精确的加表零偏和比例因子,并用于下个历元IMU原始观测值的修正.

2 GNSS/INS紧组合抗差估计方法

残差标准化[10-11]的步骤分为求解残差和残差对应的方差协方差矩阵,利用残差及其对应的方差协方差矩阵对角线元素的平方根,求解对应的标准化残差.

再利用IGG3模型[10]构建相应的粗差处理策略,降低粗差对于定位结果的影响,相应的模型为:

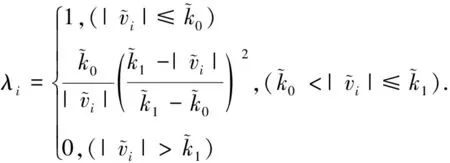
(9)

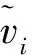
图1 RTK/INS抗差Kalman滤波流程图

3 RTK/INS紧组合算例分析

3.1 实验数据

为了验证算法的正确性,进行了两组实测实验.数据采集于2018年1月19日和2018年7月20日,移动站GNSS接收机是Trimble NetR9,采用的惯性器件参数如表1所示.采集地点为湖北省武汉市江夏区两个区域,如图2和3所示.两组实验均采用的是GPS和BDS双系统,采样率为1 Hz的双频观测值.其中第二组实验数据中,大部分的GPS观测值为单频观测值,导致GPS双频观测值数量不足,无法得到模糊度的固定解,如图4所示.图4中灰色线条表示单频数据,深色线条表示双频数据,可以看出第二组的数据质量偏低.图5、6为两组数据的共视卫星数图,可以看出在动态环境下,卫星数变化剧烈.

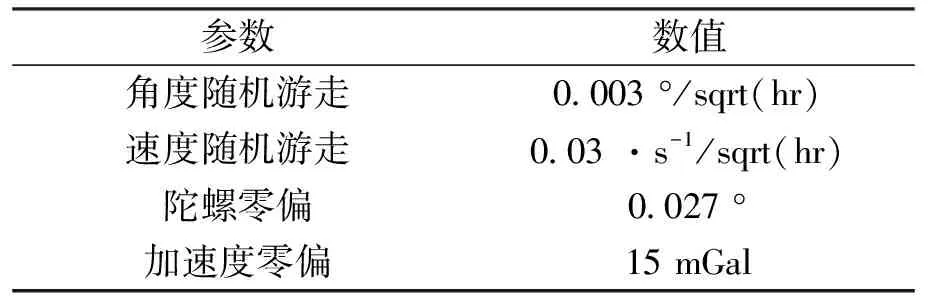
表1 惯性器件参数表

图2 第一组车载路线

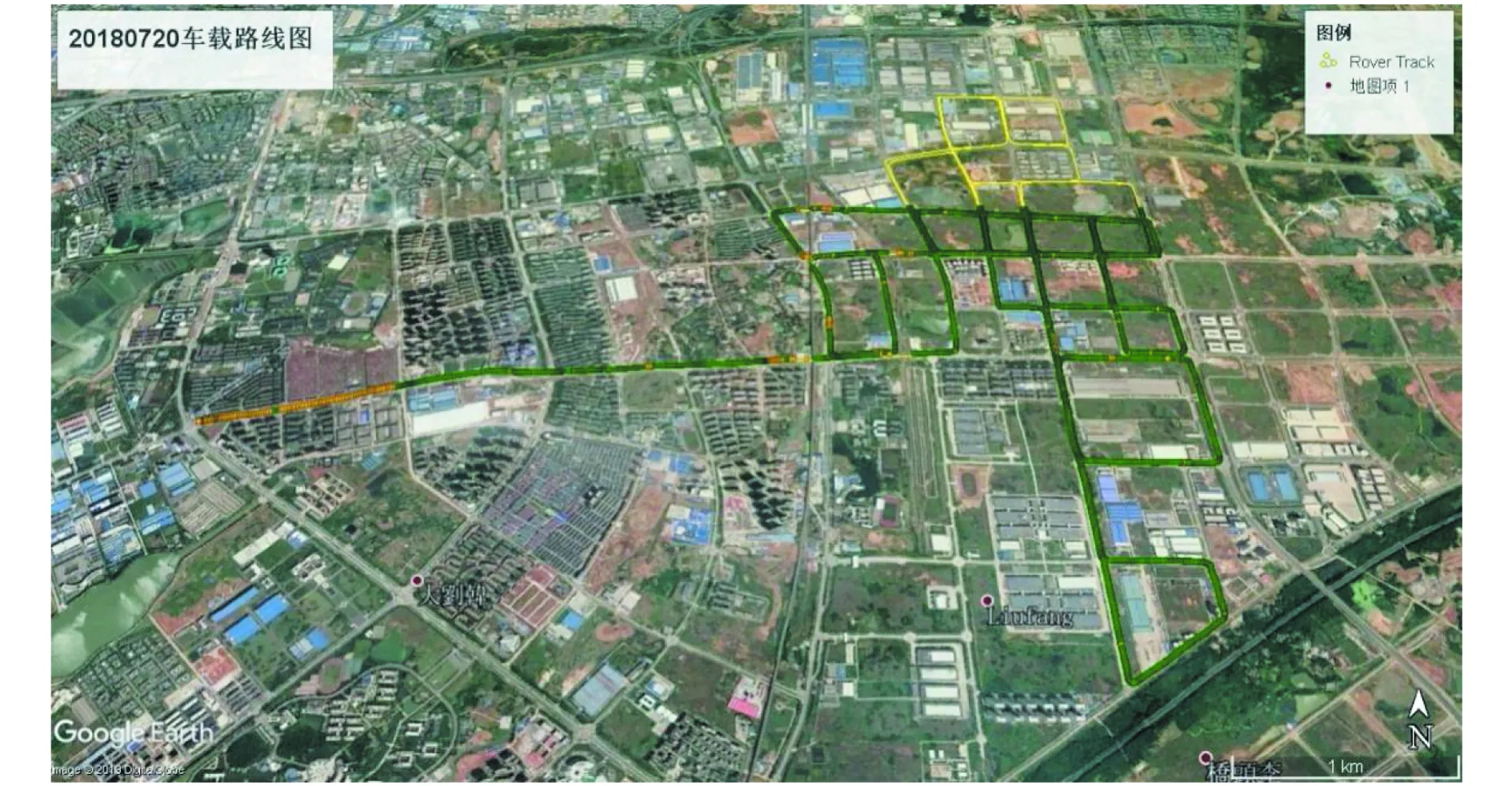
图3 第二组车载路线

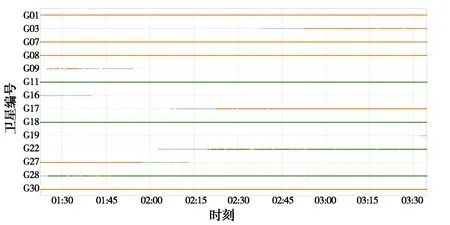
图4 GPS可见卫星数

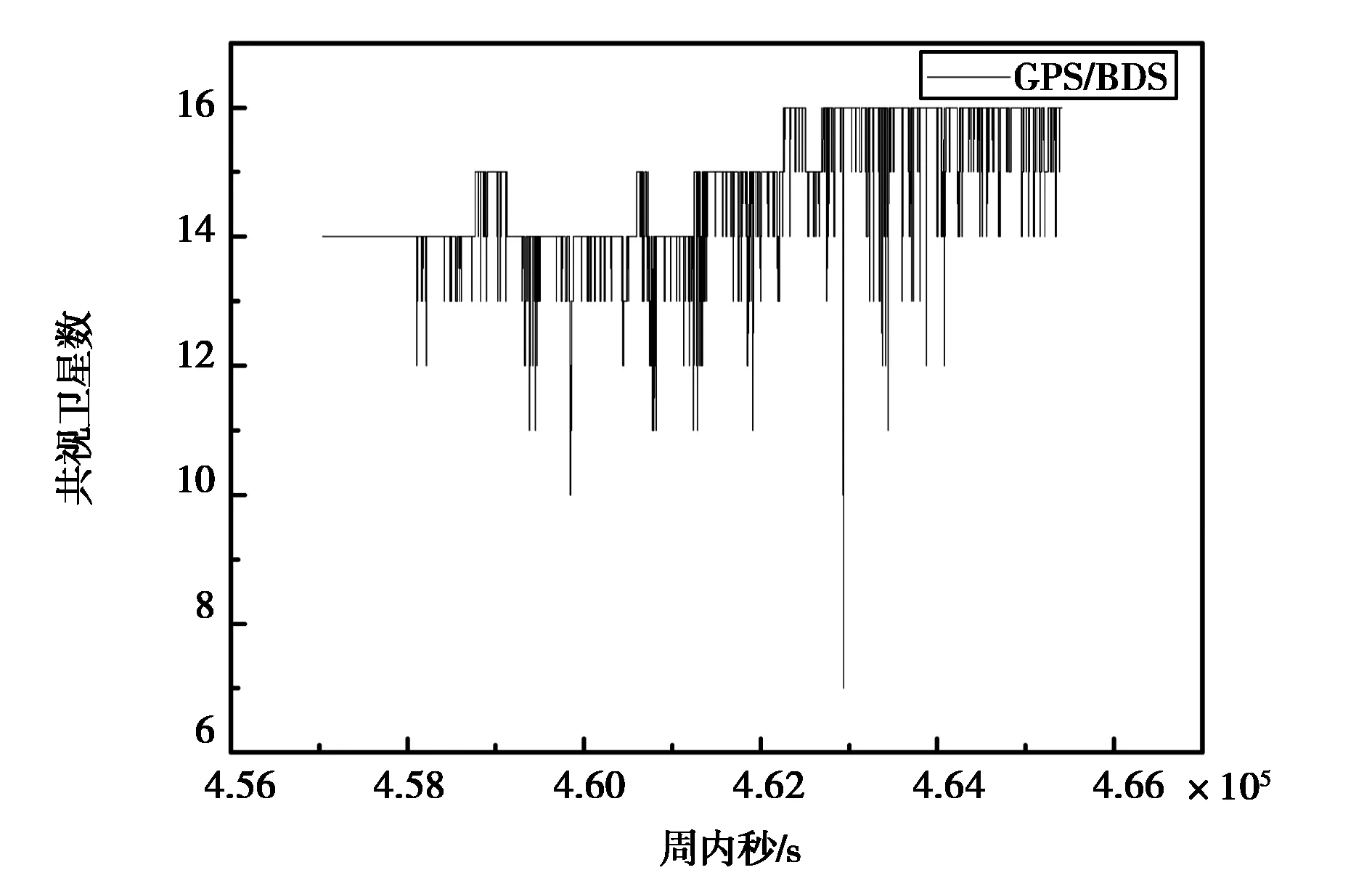
图5 第一组数据的共视卫星数

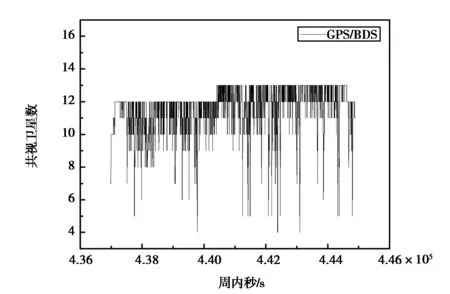
图6 第二组数据的共视卫星数

3.2 解算策略及结果分析

为了验证上述算法的有效性,做以下两组对比试验:一组使用传统EKF算法,不利用INS推算出来的位置和方差进行任何粗差剔除;第二组使用本文提出的抗差EKF,即Robust EKF.图7～8为第一组车载数据的Robust EKF和EKF结果图,表2示出了相应定位结果均方根(RMS)值的提升幅度.

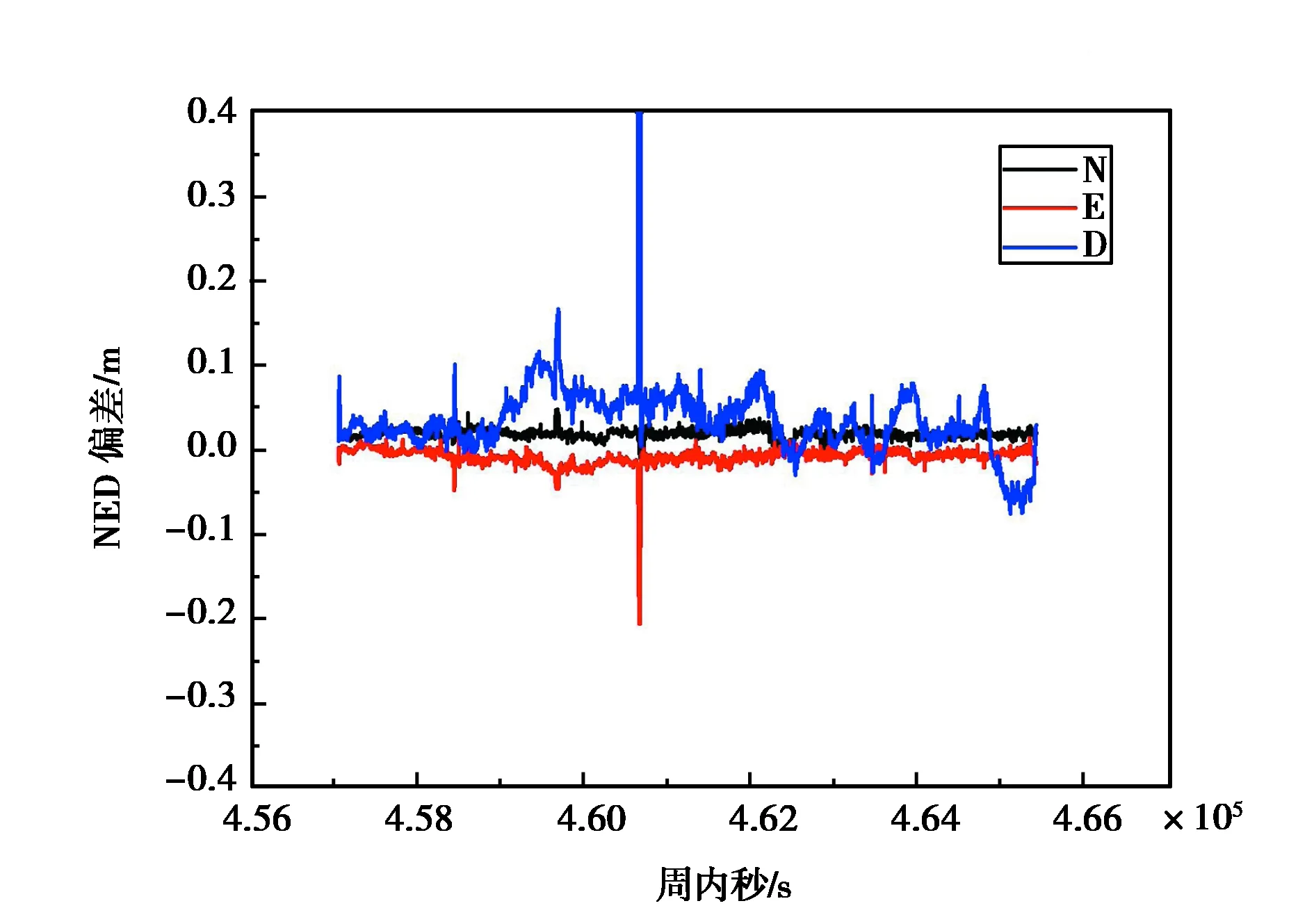
图7 Robust EKF定位结果

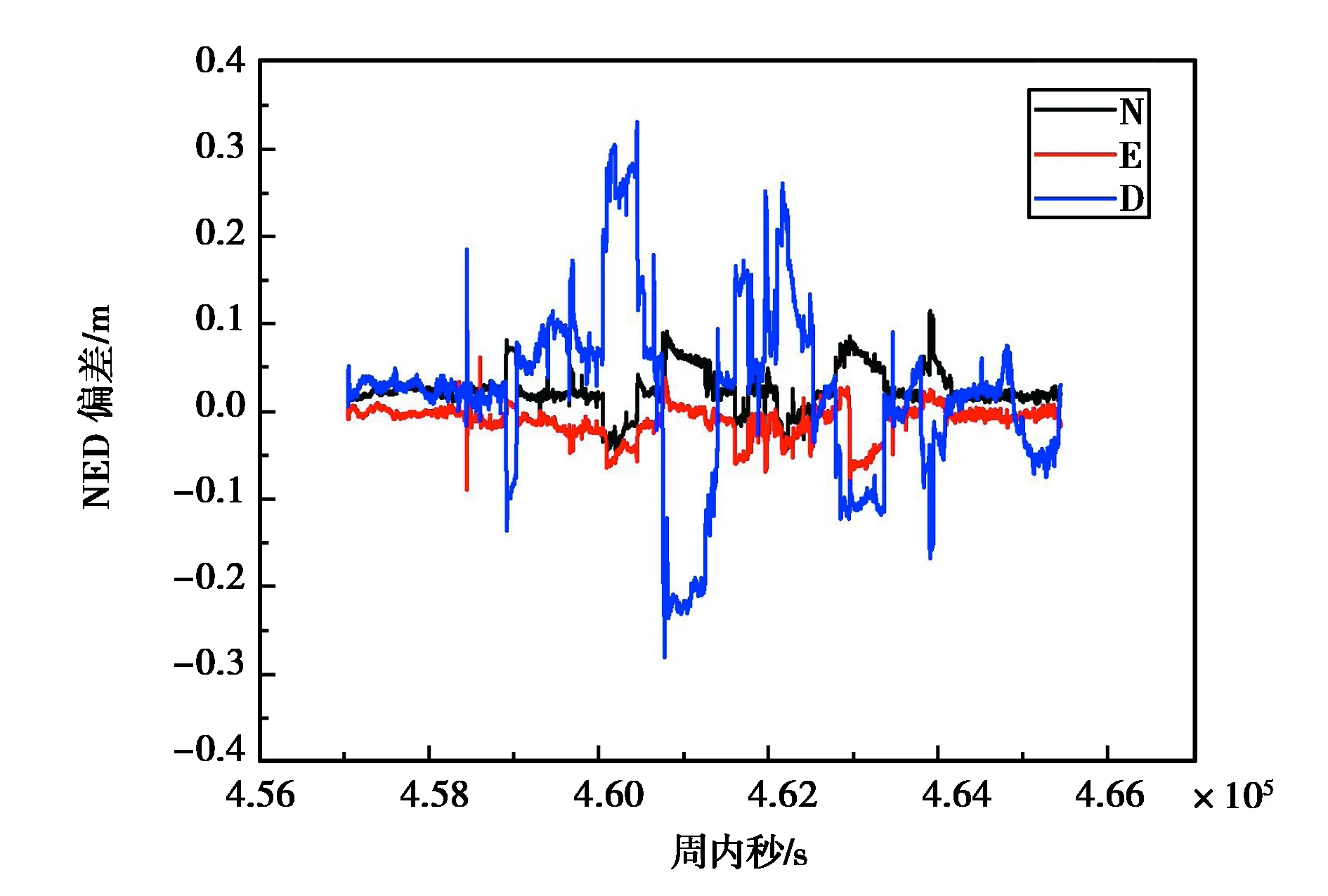
图8 EKF定位结果

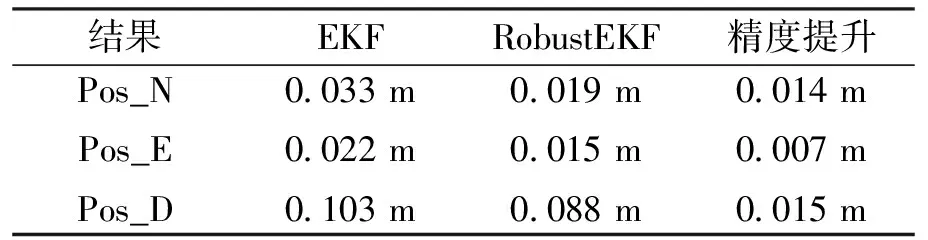
表2 EKF与Robust EKF结果对比

结果EKFRobustEKF精度提升 Pos_NPos_EPos_D0.033 m0.022 m0.103 m0.019 m0.015 m0.088 m0.014 m0.007 m0.015 m

如图8所示,不采用抗差的EKF方法,基线的起伏变化明显,相较而言,Robust EKF的定位结果整体平滑且稳定.EKF无法利用INS的先验信息剔除小周跳和伪距粗差,使得滤波结果出现明显的波动.从表2中可以看出,与传统的EKF相比,Robust EKF的定位结果在N、E、D三个方向上分别有1.4 cm、0.7 cm、1.5 cm的提升.

如图9所示,第二组数据,不采用抗差的EKF方法,基线的三方向都出现了严重偏离参考值的现象,且结果有很多突刺,特别是D方向,而图10所示的Robust EKF在整体定位的精度和稳定性均有提高,说明对不同精度的观测值扩大相应倍数的方差,有助于减少粗差对定位结果的影响.从表3中可以看出,与传统的EKF相比,Robust EKF的定位结果在N、E、D三个方向上有4.6 cm,9 cm,2 cm的提升,但是Robust EKF也出现了一个非常明显的突刺,主要是D方向有较大的偏差,下文有进一步分析.

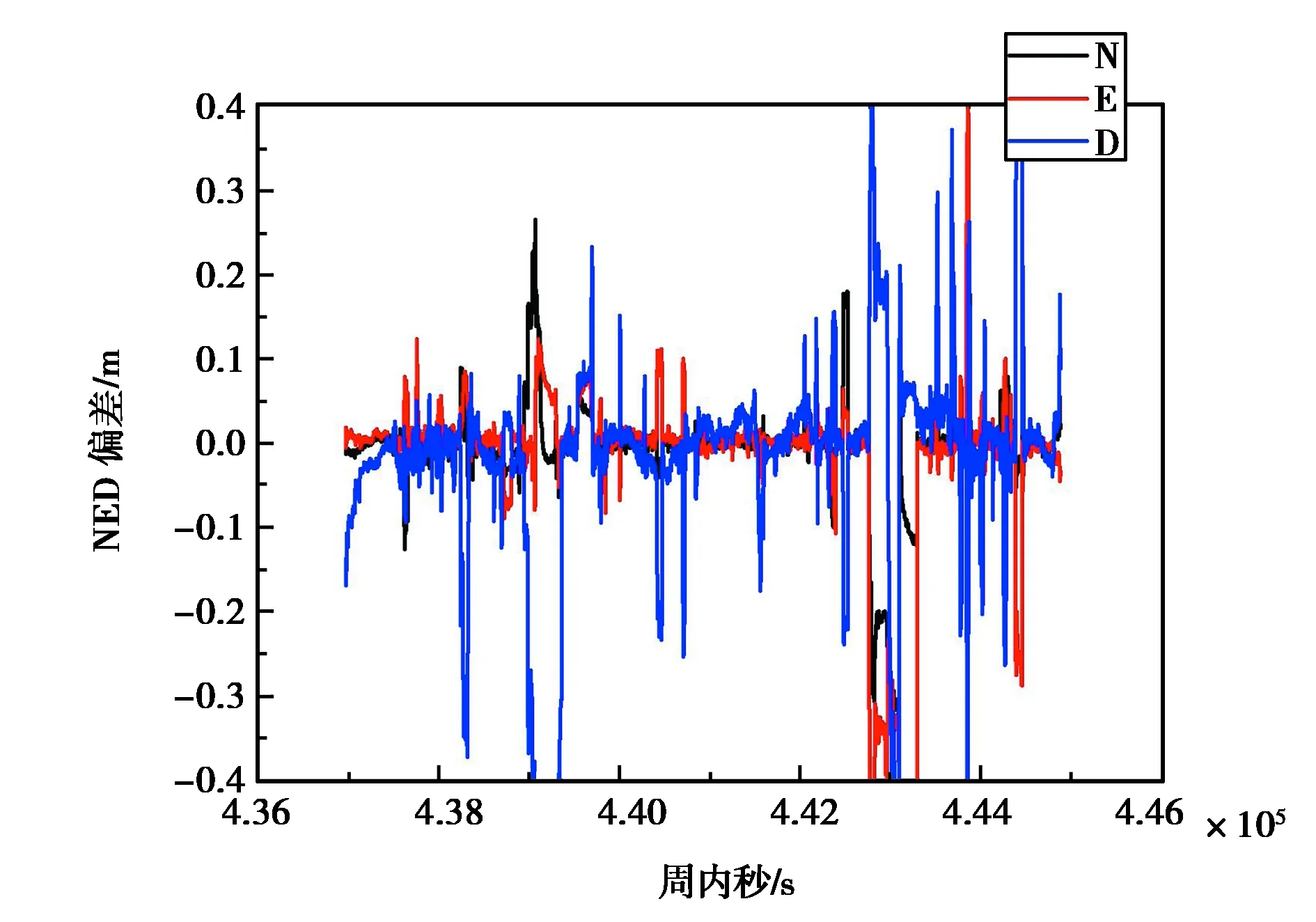
图9 EKF定位结果

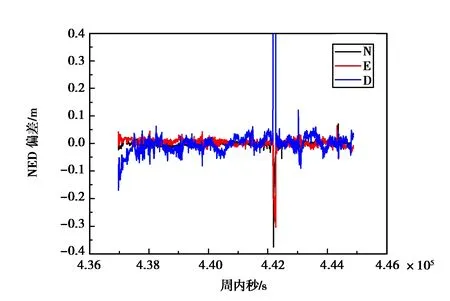
图10 Robust EKF定位结果

表3 EKF与Robust EKF结果对比

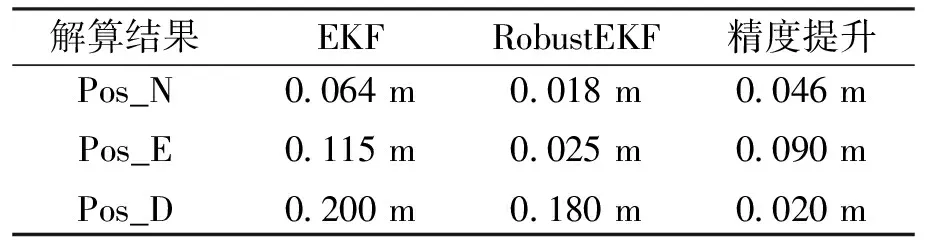
解算结果EKFRobustEKF精度提升 Pos_NPos_EPos_D0.064 m0.115 m0.200 m0.018 m0.025 m0.180 m0.046 m0.090 m0.020 m

本文采用的是全模糊度固定,当有新卫星或者粗差出现的时候,浮点模糊度的精度就会受到影响,且可能导致该历元的模糊度固定失败.从表4可以看出,与EKF相比,Robust EKF的全模糊度固定成功率分别提升了25.6%和10.3%.为分析产生抗差前后的效果,此处给出了第二组数据(精度较差的一组)的验后残差图,如图11～12所示.

表4 全模糊度固定成功率

与第一组数据相比,第二组数据的卫星数变化更加剧烈,故以第二组数据为例进行分析.从图 11～12可以看出对应图7中模糊度未固定区域(残差较大区域),Robust EKF相较于EKF,整体上更加平稳,Robust EKF载波相位的验后残差的均值为0,STD为0.014 m,RMS为0.014 m,而EKF的载波相位验后残差的均值已经偏离了0均值,且STD和RMS比相应的Robust EKF大了0.012 m.

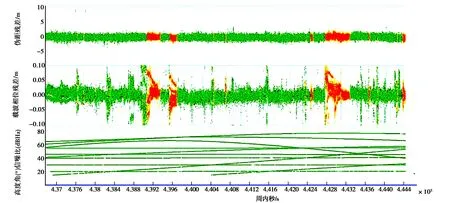
图11 第二组实验的EFK验后残差

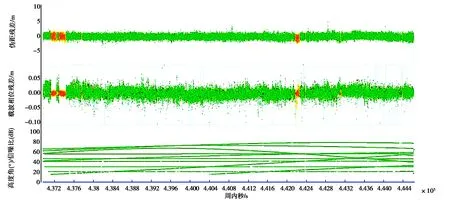
图12 第二组实验的Robust EKF验后残差

针对两组实验结果中突刺现象,现分析了两组数据对应时间端的共视卫星数,如图13～14所示.

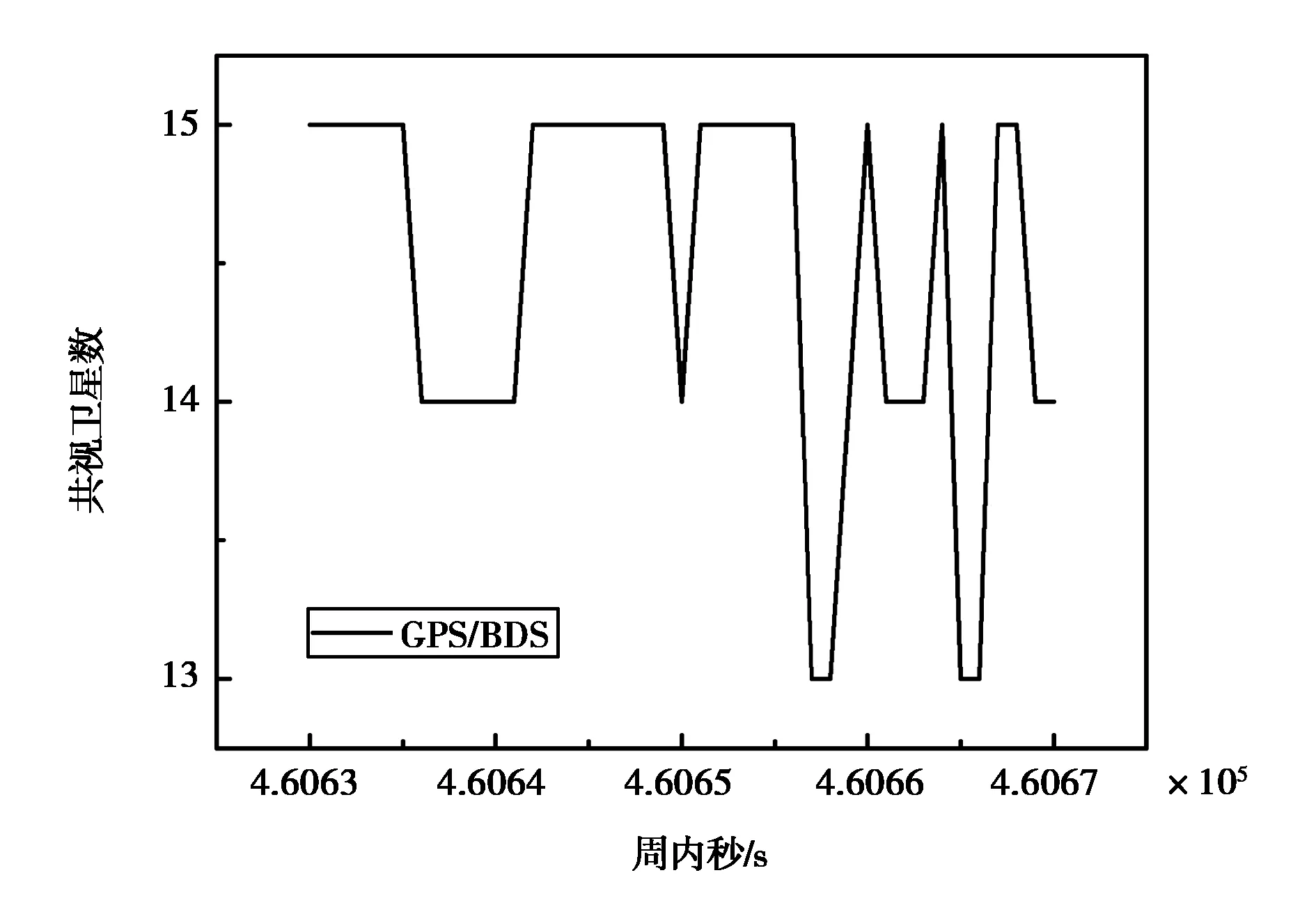
图13 第一组突变时段的共视卫星数

图14 第二组突变时段的共视卫星数

可以看出,该段出现了卫星数的连续变化,ratio值也稳定在1.0左右.造成该突刺的原因也有可能是周跳在这段时间内均未探测出来,或是传递了错误的模糊度,并且在该段时间内没有检测到该周跳,从而产生了一段连续时段的位置偏差.

4 结束语

本文提出了一种基于抗差卡尔曼滤波的RTK/INS紧组合导航定位算法,根据方差膨胀模型,建立了抗差卡尔曼算法,考虑利用相位双差和伪距双差的粗差检验量来共同降低粗差的影响,并通过实测车载实验进行了算法验证.实验结果表明:在两组实验中,加入抗差策略后,在N、E、D三个方向上分别有1.4～4.6 cm,0.7～9 cm,1.5～2 cm的精度提升,模糊度固定成功率提高10.3%～-25.6%,误差曲线也更加平滑,稳定性更高.但是在两组数据中都出现了相同类型的突刺现象,特别是D方向上产生了米级左右的误差,可能原因为：1)由于该时间段观测卫星数的连续变化；2)该方法是连续两次超限才重置模糊度,可能导致出现了周跳的情况下,并未及时重置,导致出现定位粗差；3)并未统计卫星的持续跟踪历元数,从而根据持续跟踪历元数有选择性地拒绝估计某些卫星的模糊度.去除该部分之后,D方向的RMS将稳定在厘米级,提供更加稳定可靠的定位服务.后续实验将着重分析和解决模糊度固定错误、周跳未探明等问题,使得结果稳定性更高.

致谢:感谢武汉大学卫星导航定位研究中心牛小骥老师团队提供的数据.