基于卷积神经网络的心电信号分类研究

瞿文凤

摘  要：心电图（ECG）信号基本上与人体心脏的电活动相对应，所以心电图通常在医疗领域被用来检测心血管疾病。通过计算机对心电信号进行自动分类，可以帮助医生更有效地进行心血管疾病的诊断，提高准确率。该文提出了一种一维卷积神经网络模型，可从原始心电数据中提取有效特征并实现自动分类。该模型实现了对5种典型心律失常信号的分类，即正常心搏（N）、室上性早搏（S）、室性早搏（V）、心室融合心跳（F）、未分类心跳（Q）。在MIT-BIH心律失常数据库上的实验结果表明，该方法的分类准确率较高，达到了97.8%，并且稳定性也较高。

关键词：卷积神经网络  心电信号分类  小波变换  心律失常

中图分类号：TP391    文献标识码：A 文章编号：1672-3791（2019）08（b）-0008-04

当代社会，心血管疾病已经成为威胁人们生命健康的重大杀手[1]。心律失常作为心血管疾病中发病率最高的典型之一，对其进行精确的分类一直是生物医学领域的研究热点。

心电信号检测是诊断心律失常最有效的手段之一。传统诊断心律失常的过程一般需要有经验的心脏病专家仔细研究心电图，既繁琐又费时。因此，在过去的几十年里，计算机辅助诊断（CAD）算法被应用于心律失常的自动分析，算法主要包括信号预处理、波形检测、特征提取和疾病分类4个步骤[2]。这种传统的基于机器学习的研究方法虽然在特定的数据集上取得了较为显著的研究成果，但其严重依赖人工设计特征，算法工作量大，所以在实际应用中尚未达到令人满意的效果。

近年来，随着人工智能技术的兴起，以卷积神经网络（Convolutional Neural Network，CNN）为代表的深度学习技术发展火热，其优势在于可以通过训练网络参数从海量数据中自动学习得到深层次特征而无需人工设计特征，其在多种任务，例如图像分类与定位、语音識别等领域都展现出了十分强大的性能[3]。虽然CNN在图像识别领域应用比较广泛，但是ECG信号具有与图像比较相似的局部与整体的相关性，因而也可以将CNN应用到ECG信号处理领域，该文处理的ECG心拍是一维信号，故该文所提出的CNN模型也是一维的。该模型可以直接对以下5种ECG心律失常类型进行分类，包括正常心搏（N）、室上性早搏（S）、室性早搏（V）、心室融合心跳（F）、未分类心跳（Q）。这5种类型是根据AAMI的标准划分的。

1  方法

1.1 数据预处理

1.1.1 数据降噪

心电信号是一种微弱的生理电信号，易受噪声干扰。常见的噪声主要包含肌电干扰、基线漂移和工频干扰[4]这三种。为了提取有用的心电信息，必须要对心电信号进行降噪处理。因此，该文通过结合小波阈值法和小波分解重构算法[5]进行噪声的滤除。其中，小波阈值法通过设置一个合适的阈值将阈值以下的噪声系数置零，保留阈值以上的信号系数，然后对阈值处理后的小波进行信号重构，得到降噪后的信号。采用小波分解重构算法将原始信号分解为多级，每一级分解为高频和低频信息。最后，通过确定有效信号的频率范围对信号进行重构，即可得到降噪后的信号。通过这两种算法的有机结合，前者可以有效地滤除肌电干扰和工频干扰，后者进行基线漂移的校正，从而完成信号降噪工作。

1.1.2 数据分段

心电信号进行降噪处理后，由于一条充分长的心电记录中包含的信息太多，可能包含了很多种类型的心拍，直接全局处理不利于精细的识别，故而需要对其进行分段处理。首先进行R波峰的检测。常用方法是小波变换[6]。该文在样条小波的基础上，采用B-样条小波函数作为尺度函数，将心电信号进行4个尺度的小波分解，得出模极大值对过零点，即对应R波峰值点。在成功检测出R波峰后，以R点位置为基准分割信号。在R点左右两侧选取100个采样点，可得到一段长度为201个采样点的心电信号，然后，运用下采样函数将心电数据长度减少到130个采样点。本工作共提取到109450个心电样本数据。

1.1.3 数据扩充与归一化

数据的扩充可以有效地减少过拟合，保持类之间的均衡分布[7]。根据心电类数据具有周期性的特点，通过“平移起点法”，包括N、S、V、F、Q等5类的心电样本总数增加到453050个。最终利用Z-score归一化方法[8]对每个样本数据进行归一化，解决幅值缩放问题，消除偏移效应，经过处理后的心电信号可直接输入到CNN模型中进行训练和测试。

1.2 CNN模型

该文所提出的CNN模型主要由特征提取和分类两部分组成。特征提取部分负责对心电信号自动提取有效特征，而分类部分负责利用提取的特征对心电信号进行准确分类。

1.2.1 特征提取部分

特征提取部分主要由卷积层和池化层组成。卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法最优化得到的。卷积运算的目的是提取输入的不同特征，从低级特征中迭代提取更复杂的特征。卷积层的输出表达式如式（1）所示：

（1）

其中Xjl为对应于第l层的第j个卷积核的特征向量;Mj为当前神经元的感受野（接受域）;而Wij1为分配给第l层的第j个卷积核的权重系数;f（*）为一个非线性激活函数。

池化层（亦名下采样层），其具体操作与卷积层的操作基本相同，只不过池化层的卷积核只取对应位置的最大值、平均值等（最大池化、平均池化），并且不经过反向传播的修改。其作用是可以忽略目标的倾斜、旋转之类的相对位置的变化，以此提高精度，同时降低了特征图的维度并且一定程度上可以避免过拟合。其公式如式（2）所示：

（2）

其中down（*）为下采样函数;βjl为权重系数;bjl为偏置系数。

1.2.2 分类部分

分类部分主要是全连接层。全连接层是将经过多个卷积层和池化层的特征图中的特征进行整合，获取特征具有的高层含义，之后用于分类。

1.2.3 1D-CNN模型

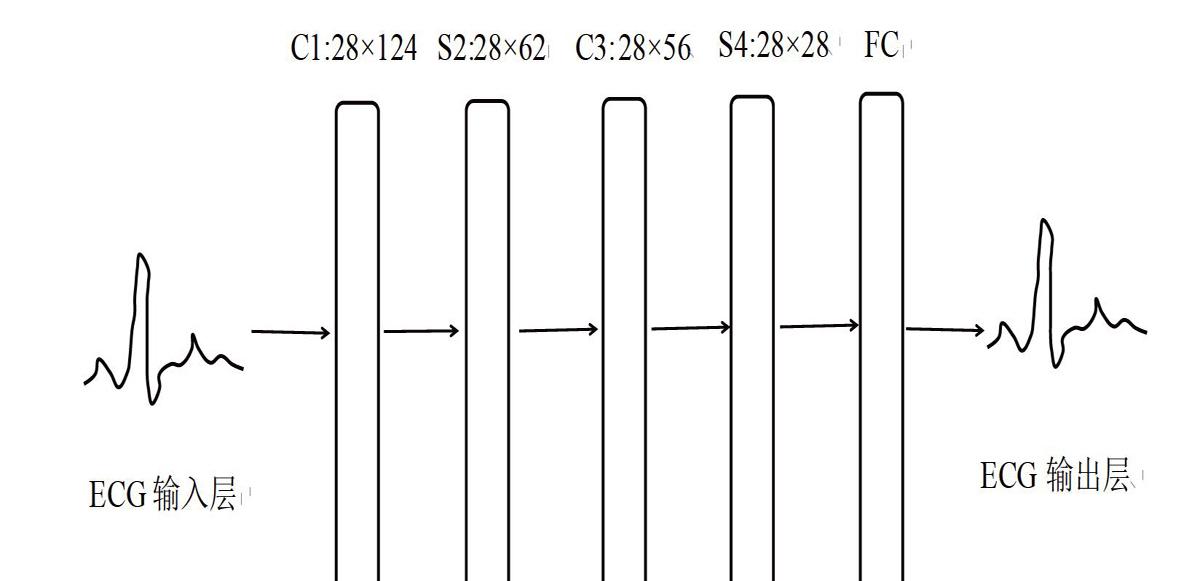
CNN通常运用于图像领域，处理二维数据。基于心电信号是一维的，故该文对CNN模型进行了调整。优化后的CNN心电分类模型如图1所示。其基本结构包括一个输入层、两个卷积层（C1、C3）、两个池化层（S2、S4）、一个全连接层（FC）和一个输出层。通过卷积层和池化层交替执行提取特征，并将提取到的特征作为全连接层的输入进行分类。

在卷积层C1中，使用28个7×1的卷积核对输入的ECG 信号进行卷积操作，得到28个特征图，每个特征图的大小为（1×124）。在池化层S2中，对C1的每个特征图进行尺度为2×1的最大池化操作，特征图个数仍为28，经池化之后每个特征图的大小为（1×62）。C3也设置了28个卷积核，用7×1的卷积核对S2进行卷积，此时特征图大小为（1×56）。在S4层中，对C3的每个特征图进行尺度为2×1的最大池化操作，特征图个数为28，此时特征图的大小为（1×28）。FC是一个全连接层，输出层设置5个神经元，使用Softmax函数分别输出每个类，即N、S、V、F、Q这5种类型。

2  实验与结果分析

2.1 实验数据

该文所使用的数据集来源于MIT-BIH心律失常数据库[9]。该数据库包含48组记录，每组记录时长约30min，采样率为360Hz。并且每组记录均包含两个导联的ECG数据。基于该实验研究的是一维模型，故从每组记录中选取第II导联的心电图记录共44条，来训练验证该方法的可行性。根据AAMI标准[10]，（102，104，107，217）这4条记录被排除，因为这些记录在后期处理时信号质量较差。

2.2 实验结果

该文采用了十倍交叉验证策略[11]。将生成的心电样本数据随机分为10等份。基于提出的模型，其中的9份被用作训练集，剩余的1份被用于测试集，交叉验证重复10次实验。然后，在每一次实验中评估性能指标（准确率、灵敏度和特异性）。最后，通过评估10次结果的平均值，得到算法总体性能。

2.2.1 卷積层参数的选择

在卷积层中，卷积核的大小和数量可以影响到模型的质量，当学习率一定时，为了使得模型最优化，该文进行了4组对比实验。在每组实验中所设置的卷积核个数不同，分别为3，5，7，9。实验结果表明，4组实验的错误率随卷积核个数的增加而变化。当卷积核大小分别为7和9时，实验错误率随卷积核个数的增加而改变的趋势相对稳定。并且当特征图个数为28时，错误率几乎达到最小值。Lecun最近的评论表明，在计算精度相同的情况下，选择较小尺寸的卷积核更好。为了防止卷积核尺寸过大而导致计算复杂，该文最终确定卷积核的大小为7，每层特征图的最优个数为28。

2.2.2 学习率的选定

为了研究学习率对错误率是否有影响，在卷积核大小和数量固定的情况下，该文设定了不同大小的学习率，研究实验的错误率和训练时间。实验结果表明，当学习率小于0.1时，实验错误率都是2.5%左右。然而随着学习率的提高，训练时间也逐渐减少。例如，当学习率为0.001时，收敛速度最慢;反之，当学习率为0.1时，数据收敛速度更快，训练时间最短。当学习率大于0.1时，错误率呈不规则变化，时而增加，时而减少。据认为，这种现象是由于学习率过快，导致数据无法收敛。总之，不仅要保证正确率，还要设定合适的学习率来减少训练时间。所以该文最终选定学习率为0.1。

2.2.3 迭代次数的选择

为了准确研究迭代次数与测试正确率之间的关系，该文在固定卷积核大小、数量和学习率的前提下，通过调整迭代次数来评估测试集的正确率。实验结果表明，随着迭代次数的增加，错误率呈下降趋势并逐渐趋于平稳。当迭代次数为50时，错误率高达15%;而迭代次数达到300时错误率为3.5%。当迭代次数设置为300、350、400时错误率保持不变。此时，需要考虑训练时间。当其他参数固定时，每个训练步骤的时间成本是相似的，训练越多，所需时间越长。

2.2.4 性能评价

CNN模型比较消耗计算资源，而且神经网络的任何变化都需要新的训练，这会非常消耗时间和资源，这个方面需要优化和重视。所以该文选择所有阶段的最优参数，在上述优化参数的基础上得到训练模型，其中模型的学习率设为0.1，两层卷积层的卷积核大小均为7。对于最大池化操作，两个池化层的采样因子都为2，迭代次数为300次。最后的测试结果表明，该方法的准确度为97.8%。实验结果的混淆矩阵如表1所示。其中N、S、V、F、Q分别代表5种心律失常心拍类型。

最后，该文还与前人研究的心电分类算法进行比较。如表2所示，与以前研究者所提出的方法和实验成果相比，该文所提出的方法提高了心电分类的准确率。

3  结语

心电信号是用于诊断和预防心律失常等心血管疾病的有效手段，对其进行精确的分类具有重要的临床意义。该文在前人研究的工作基础上，提出了一种一维的卷积神经网络模型，首先对MIT-BIH心律失常数据库的数据利用小波变换相关算法进行预处理操作，再将经过预处理的心电数据输入到CNN模型中进行训练和测试。最后经实验验证该文所提出的模型可有效地对N、S、V、F、Q等5种心律失常类型进行分类，且分类的稳定性和准确率较高，为进一步提高心电图自动分类的效果实现了有益的探索。

参考文献

[1] 陈伟伟，高润霖，刘力生，等.《中国心血管病报告2016》概要[J].中国循环杂志，2017，32（6）：521-530.

[2] Selcan Kaplan Berkaya， Alper Kursat Uysal， Efnan Sora Gunal， et al. A survey on ECG analysis[J].Biomedical Signal Processing and Control，2018（43）：216-235.

[3] Chatfield K， Simonyan K，VedaldiA， et al. Return of the Devil in the Details： Delving Deep into Convolutional Nets[J].Computer Science，2014（156）：52-54.

[4] Alyasseri ZA，Khader AT，Al-Betar MA，et al. Hybridizing beta-hill climbing with wavelet transform for denoising ECG signals[J].InfSci（Ny），2018（429）：229-246.

[5] 焦运良，邢计元，靳尧凯.基于小波变换的心电信号阈值去噪算法研究[J].信息技术与网络安全，2019，38（5）：62-66.

[6] Ismaiel，Fatima Osman Mohamed. Classification of Cardiac Arrhythmias Based on Wavelet Transform and Neural Networks[D].Sudan University of Science&Technology，2015.

[7] Paolo Vecchiotti， Giovanni Pepe， Emanuele Principi， et al. Detection of activity and position of speakers by using Deep Neural Networks and Acoustic Data Augmentation[J].Expert Systems With Applications， 2019.

[8] Jin Lin-peng， Dong Jun. Deep learning research on clinical electrocardiogram analysis[J].Science China： Information Sciences，2015，45（3）：398-416.

[9] Ritu Singh， Rajesh Mehta，Navin Rajpal. Efficient wavelet families for ECG classification using neural classifiers[J].Procedia Computer Science，2018（132）：11-21.

[10] Brian Young，Johann-Jakob Schmid.Updates to IEC/AAMI ECG standards， a new hybrid standard[A].Journal of Electrocardiology[C].2018.

[11] Han Meng，Ding Jian.An improvement and implementation of BP algorithm based on cross-validation[J].Computer Engineering and Design，2008，29 （14）：3738-3739.

[12] N.P.Joshi， P.S.Topannavar， Support vector machine based heartbeat classification[A].In Proc.of 4th IRF Int. Conf[C].2014：140-144.

[13] M. Zubair，J. Kim，C.Yoon. An Automated ECG Beat Classification System Using Convolutional Neural Networks[A].International Conference In IT Convergence and Security（ICITCS）[C].2016：1-5.

[14] Wei Jiang， Seong G，Kong. Block-based neural networks for personalized ECG signal classification[J].IEEE Transactions on Neural Networks，2007，8（6）：1750-1761.

[15] 陳宇飞，张博，林楠，等.一种高效检测心律不齐的深度学习算法[J].小型微型计算机系统，2018，39（11）：2436-2440.