环形智能加工系统中RGV的动态调度策略
袁梦婷


摘要:基于MDP理论,将“RGV执行并完成任务所需时间”构建为动态优先级,引入随机变量“CNC发生故障和排除故障的时间”,结合RGV、CNC、物料的状态变化情况,建立基于MDP理论的状态转移模型。并在数值迭代算法的基础上设计了MDP迭代寻优算法对三组系统进行求解,从而得到一道工序物料加工过程中,CNC有1%的概率发生故障的情形下环形智能加工系统在未知动态环境下的最优调度策略。
Abstract: Basing on the MDP theory, we construct the time of RGV to execute and complete the task as the dynamic priority, and introduce two random variables, the time when the CNC is faulty and the fault is removed. At the meanwhile, combining with the state changes of RGV, CNC and materials, we establish a state transition model based on MDP theory. Then, based on the numerical iterative algorithm, the MDP iterative optimization algorithm is designed to solve the three groups of systems, so that the optimal scheduling strategy of the intelligent processing system in an unknown dynamic environment during the processing of a process material with a 1% probability of failure in the CNC is obtained.
關键词:MDP理论;动态优先级;迭代寻优算法;动态调度最优策略
Key words: MDP theory;dynamic priority;iterative optimization algorithm;dynamic scheduling optimal strategy
中图分类号:TP273 文献标识码:A 文章编号:1006-4311(2019)27-0043-03
0 引言
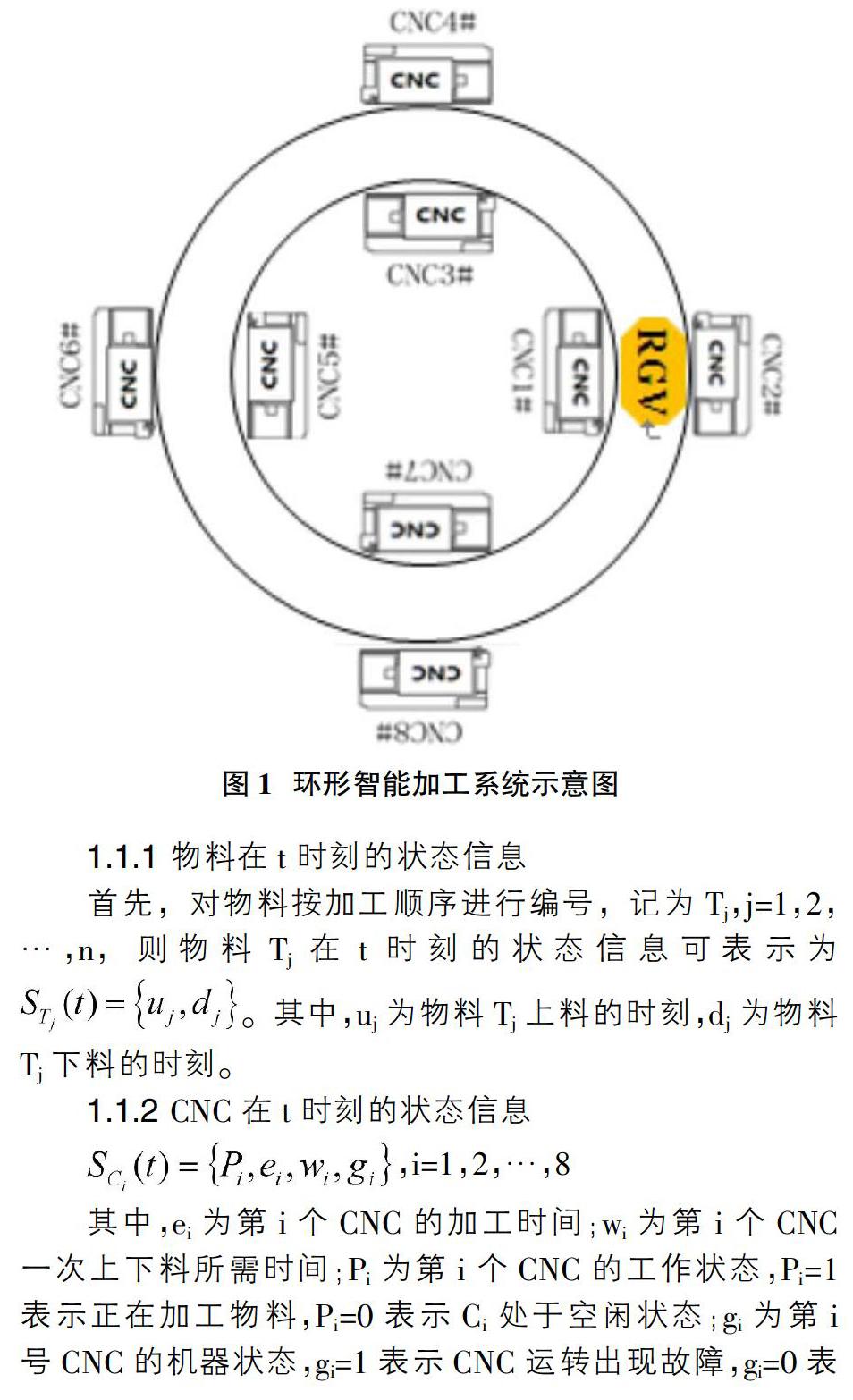
随着当今世界科学技术的蓬勃发展,现代物流观念渐渐深入人心。为解决庞杂的物流问题,自动化物流系统开始兴起,然而如何合理地设计智能加工系统的调度策略从而提高效率是自动化系统的核心。如今,已有大量研究者致力于解决RGV的动态调度策略。张桂琴等[1]设计了RGV的智能调度算法和避碰防撞算法,解决了2辆RGV的相向碰撞和同向追尾问题;沈艳等[2]针对网络控制系统中采样周期时变不确定性对控制和运行性能的影响,提出了基于反馈控制原理和预测机理的动态调度策略;查振元等[3]着重分析了RGV的应用。这些虽然给出了很多解决各种情况下的调度策略,但是没有对实际加工情境进行分析。因此本文主要以图1所示的环形智能加工系统为例(RGV固定逆时针移动),研究一道工序物料加工过程中,CNC有1%的概率发生故障的情形下环形智能加工系统在未知动态环境下的最优调度策略。
1 基于MDP理论的状态转移模型
1.1 状态分析
本文将系统端视为观察者,RGV视为决策者,以RGV执行并完成任务所需时间为动态优先级,时间越短优先级越高为决策依据,使RGV做出决策并执行任务,从而使各CNC的运转状态发生改变。并以RGV位于CNC1#和CNC2#正中间,所有CNC都处于空闲状态为初始状态,分别对物料、CNC及RGV的状态进行分析。
1.1.1 物料在t时刻的状态信息
1.1.2 CNC在t时刻的状态信息
由于在加工过程中,我们无法判断CNC何时出现故障,因此对它设定随机变量ε1,其范围为0到对应CNC加工一个物料所需时间,使CNC在加工过程中的某个时刻出现概率为1%的故障,无法正常加工。同理,由于故障排除时间在10~20分钟内,我们无法确定每次故障排除的准确时间,因此再设定随机变量ε2,其范围为600s至1200s,使CNC发生故障后的10~20分钟的某个时刻恢复正常运转状态。
1.2 建立模型
1.2.1 动态优先级的构建
为提高系统工作的效率,本文建立RGV执行并完成任务所需时间T为其决策的动态优先级,RGV将在发出信号的CNC数量大于1时根据动态优先级进行判断,并做出决策,T越小,优先级越高,任务越先被执行。
1.2.2 状态转移模型
1.3 模型求解
1.3.1 模型的求解算法——MDP迭代寻优算法
由于智能加工系统处于一个动态变化的过程,因此每一次决策的任务分配都会影响到整个系统的总体效率,为了满足加工系统动态任务分配的快速性要求,根据MDP最优策略的存在性判定定理[5],我们所建立的基于MDP理论的状态转移模型一定存在最优策略,可用数值迭代算法进行求解。结合本文实际情况,我们在数值迭代算法的基础上进行优化,设计了MDP迭代寻优算法。此算法在迭代的过程中可计算出在可能发生故障的情况下,RGV每次分配任务后整个系统的状态,最终求解出最优动态调度策略。
1.3.2 求解结果
考虑CNC可能会发生故障的情况,依据基于MDP理论的状态转移模型,结合MDP迭代寻优算法,利用相关系统作业参数,我们通过MATLAB软件,求解得到一道工序物料在有故障情形下RGV的最优动态调度策略。(表1)
1.3.3 敏感性分析
由于CNC发生故障情形中存在随机变量,使得结果在每次算法的运行后都不一样,因此本节主要分析本文中基于MDP理论的状态转移模型的敏感性。又由于不同故障数对结果影响大致相同,故在此我们以第1组为例进行具体分析。
给予清洗时间在[-1,1]范围内以0.1为间隔的误差,运用MATLAB软件,将结果绘制成折线图,从而更清晰得反映结果的变化,如图2所示。
观察图2可以发现,参数的误差对模型的结果有一定的影响,但是影响程度较小,即模型的敏感性较低,从而证明了基于MDP理论的状态转移模型具有较高的可靠性。
2 结论
对比智能加工系统实际应用情况[3],可以发现我们求解得到的结果具有一定的实际性和正确性,证明了建立的基于MDP理论的状态转移模型的实用性及MDP迭代寻优算法的有效性。
本文的特色与创新点在于,巧妙地利用了MDP马尔可夫周期性和连续性的性质,并在此基础上构建动态优先级,建立状态转移模型,同时结合迭代寻优算法对问题进行求解。
参考文献:
[1]张桂琴,张仰森.直线往复式轨道自动导引车智能调度算法[J].计算机工程,2009,35(15):176-178,181.
[2]沈艳,郭兵.网络控制系统变采样周期智能动态调度策略[J].四川大学学报(工程科学版),2010,42(01):162-167.
[3]查振元,李计星,绳润涛,张丰华,李昌臣.智能平移轨道导引车的应用[J].机器人技术与应用,2017(05):42-43.
[4]陈明,周云龙,刘晋飞,靳文瑞.基于MDP的多Agent生产线动态调度策略[J].机电一体化,2017,23(11):15-19,56.
[5]郑少慧.一类连续时间平均马氏决策平稳最优策略的存在性[J].应用数学学报,1989(02):250-256.

