智能RGV 动态调度研究

吕云龙，王孝宇，冯超杰

（华北水利水电大学，河南 郑州 450000）

1 问题分析

针对两道工序物料加工的问题分析：考虑到CNC 在加工过程中不能更换刀头，且每道工序需要在不同的CNC 上完成，因此，如何对8 台CNC 进行合理的工序刀头分配是问题研究的关键。由于不同工序所需时间不同，需要对CNC 的刀头分配进行精确的计算，但是对于每类刀头排序情况，若通过枚举法数量多、计算难度大，我们考虑运用遗传算法，将8 台CNC 当成遗传对象进行标号，利用遗传算法适用度高，每次求解局部最优解，避免局部内循环，最后得到全局最优解。在此基础上，对遗传算法得到的多种分布规律进行求解优化，选取工作效率最高的加工刀头分布模型，进而求出在规定时间内的最大工件数。针对有故障概率的物料加工问题分析：由于CNC 在加工过程中可能出现故障，故障率为1%，需要在前两种情况问题的基础上，去增加一个条件变化，即每次CNC 工作中是否会出现故障，导致物料变为废料。根据概率论的相关知识，考虑到只有在基数大的情况下，故障率才可以得到准确的体现，所以必须使得模型是最优化的，这样才能更好地根据故障发生数去调整调度模型，提高工作效率。图1 为智能加工系统示意图。

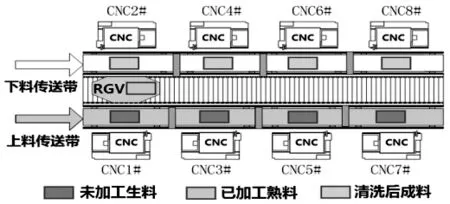
图1 智能加工系统示意图

2 模型假设

（1）CNC 的刀具不可更换。

（2）每次的加工都是完美成品，除非特别考虑故障发生概率。

（3）每个CNC 只能同时处理一个物料。

（4）RGV 每次只能拣取一件物料。

（5）RGV 运送开始的最早时间不早于上料带传送到1 号CNC 前的物料所需的时间。

3 模型的建立与求解

3.1 两道工序物料加工模型

由于两道工序物料加工情况，每个物料的第一和第二道工序分别由两台不同的CNC 依次加工完成，且每个CNC 只能同时处理一件物料，RGV 每次也只能拣取一件物料，且进行两道不同工序加工时需要用两种不同的刀头，在此智能系统中应在最初始状态还未开始加工物料时不同的CNC 就应换上不同的刀头。

（1）两道工序物料加工模型的建立。由于两道工序物料加工用两种刀头的时间各不相同，故需对不同工序刀头的个数进行优化，充分考虑实际生产情况按照两道工序时间相对差值大小确定不同类型刀头的分配，有以下三种情况：①工序时间长的刀头类型四个，工序时间短的刀头类型四个；②工序时间长的刀头类型五个，工序时间短的刀头类型三个；③工序时间长的刀头类型六个，工序时间短的刀头类型两个。

每个情况由于工序刀头的排列类型不同，又可分为若干种情况，若应用普通算法，计算量大，难以找出较优结果，故提出利用遗传算法来寻求每种情况下的两种工序刀头最优排列组合。

（2）利用遗传算法（GA）对模型进行求解。为了让智能加工系统适应连续加工以及复杂的运行环境，由于普通算法计算量较大，故提出利用遗传算法来寻找最优解。

两道工序物料加工具体步骤：

Step1：利用工序之间加工时间的相对大小，列出所可能加工工序刀头所存在的数量分配。

Step2：根据所可能存在的不同数量的加工刀头的分配，运用遗传算法选取最优的加工刀头分布模型。

Step3：RGV 按照最优加工刀头分布模型对第一道工序CNC 依次进行上料，直到完成最后一个第一道工序CNC 的上料工作。

Step4：第一道工序完成以后第一道工序CNC 发出指令，RGV 选取空闲并最近的第二道工序CNC 进行二道工序加工。

Step5：若一段时间内RGV 没有接受到指令，则RGV 在原地等待CNC 发出的指令，若有多个CNC 发出指令，则采取就近优先原则执行指令。

Step6：RGV 执行并完成CNC 指令。

Step7：重复step4，step5，step6 直到完成最后一个指令。

Step8：调度完成。

（3）两道工序物料加工模型验证。按照上述所建模型，利用已知所给智能加工系统作业参数对所提出模型进行验证。利用遗传算法算出符合工序时间的三种工序刀头数量分配情况下各自加工刀头的最优分布模型并计算出最后各自的物料的总加工数。工序一刀头四个，工序二刀头四个；此时8 小时物料的总加工数为206 个；工序一刀头五个，工序二刀头三个；此时，8 小时物料的总加工数为158 个；工序一刀头六个，工序二刀头两个；此时，8 小时物料的总加工数为107 个；则在第一组系统加工参数下8 小时最后加工出的最多总物料数为206 个，此时，加工刀头的分布为CNC1，CNC3，CNC5，CNC7 为 工 序 一，CNC2，CNC4，CNC6，CNC8 为工序二时作业效率最高。

3.2 加入故障概率的工序物料加工模型

由于故障发生概率约为1%，则理解为CNC 在运行过程中每运行一次发生故障的概率为1%，故障随机持续时间为10～20 分钟，其中无论物料进行一道工序还是进行两道工序其基本过程一样，步骤如下：

Step1：启动动态调度。

Step2：按调度方案进行生产。

Step3：突发事件或周期性调度判别，若是执行step4，若否执行step2。

Step4：CNC 初始状态修正，工件初始状态修正。

Step5：GA 进行优化调度并生成新的调度方案。

（1）两道工序物料加工模型故障分析。利用已知所给智能加工系统作业参数对所提出模型进行验证。由上述可知，在故障随机发生的基础上，在第一组系统加工参数下计算出8 个小时最后加工出的总物料数为202 个。

4 模型推广与优化

4.1 无等待RGV 调度模型

（1）无等待RGV 调度模型的建立。在两道工序物料加工模型中，RGV 在没有街道其他作业指令时，会留在原地等待CNC 指令的发出，则对原先所提出的两道工序物料加工模型的基础上进行修改，使RGV 能提前到达即将发出指令的CNC 位置，提高作业效率。

无等待RGV 调度步骤：

Step1：RGV 按原先调度方案对CNC 依次进行上料，直到完成最后一个CNC 的上料工作。

Step2：RGV 提前移动到即将发出指令CNC 的位置处。

Step3：CNC 发出指令，RGV 执行并完成其指令。

Step4：重复step2，step3 直到完成最后一个指令。

Step5：调度完成。

（2）无等待RGV 调度模型求解。按照上述步骤，利用第一组所给作业参数并按照工序一刀头四个，工序二刀头四个的分布模型进行验证求解。

通过与原先模型比较发现，在完成208 件物料两道工序加工的情况下，无等待模型比原先模型完成时间更短，但完成总物料工件数却没有增加，通过分析可知，在完成208 件物料加工后，所剩时间和CNC 只能进行物料第一道工序加工，所以再对此模型进行优化，提出下列优化模型。

4.2 CNC 可进行两工序加工模型

由于对于需进行两道工序加工的物料在进行不同工序时需要在不同CNC 上进行加工，对此进行优化，使物料在同一个CNC 上即可进行两工序加工，在实际生产过程中，若在不同的CNC 进行两工序加工时，最后往往会余量部分未进行第二道工序但已经完成第一道工序的物料，通过查阅资料可知，一个CNC 在完成一道工序后更换刀头所需时间在5 ～30s，故此时更换刀头，会提高作业效率。