薄壁微喷带喷洒宽度模型构建
邸志刚,杨路华,苟万里,王金毅
薄壁微喷带喷洒宽度模型构建
邸志刚1,2,杨路华1※,苟万里1,王金毅1
(1. 天津农学院,天津 300384;2. 中国农业节水与农村供水技术协会,北京 100053)
为了更好指导微喷带在农业灌溉系统中规划与设计,在天津市农业水利技术工程中心开展了薄壁微喷带喷洒水滴直径试验与喷洒宽度试验,考虑了微喷带喷洒水滴运动过程中受空气阻力、重力、浮力等因素,建立了基于牛顿力学与流体力学理论的微喷带喷洒水滴运动数学模型,推导了微喷带喷洒宽度理论计算式,确定了计算式中的参数,并对微喷带喷洒宽度影响因素进行分析。结果表明:微喷带喷洒宽度计算公式计算结果与实测数据吻合较好,对于不同型号微喷带相对误差均小于10%。理论计算公式及试验结果均反映微喷带喷洒宽度随着喷孔仰角呈先增加后减小变化,且当喷孔仰角为40°左右喷洒宽度达到最大。微喷带喷洒宽度理论计算公式精度较高,可广泛应用于喷洒宽度的计算,为微喷带灌溉系统规划设计提供理论依据。
灌溉;流量;模型;微喷带;喷洒宽度;工作压力;喷孔直径;喷孔仰角
0 引 言
微喷带是一种多孔出流薄壁塑料软管,能在一定工作压力下利用喷孔喷水进行灌溉。微喷带灌溉技术结合了喷灌和微灌的技术特点,是一种灌水均匀,灌水效率高的节水灌溉方式,在地区农业用水资源节约上起着举足轻重的作用[1-4]。由于微喷带具有灌水效果好、抗堵塞性能强、对作物和土壤冲击力小等突出优点,近年来在中国得到了广泛推广与发展[5-9]。但目前中国微喷带生产市场混乱,缺乏统一技术标准,无法将该技术纳入《微灌工程技术规范》[10]。因此通过试验确定微喷带喷洒宽度计算公式,对微喷带灌溉系统规划设计具有重要意义。
国内外很多学者对微喷带喷洒宽度等进行了研究,Deboer等[11]通过对单喷头开展水力试验研究,运用弹道模型研究了喷头喷洒水滴运动轨迹,并研究了喷头水滴平均直径和水滴动能。Sayyadi等[12]利用低压折射式喷头开分析工作压力、喷嘴直径和安装高度等因素对喷头喷洒宽度影响研究。脱云飞等[13]在无风有空气阻力假定条件下,基于牛顿力学与水力学理论,推导了喷头喷洒宽度理论公式,并与试验值进行对比分析。王建军等[14]通过试验研究了工作压力与喷射角度对微喷带单孔喷洒特性的影响,发现当微喷带喷射仰角度为30°时单孔喷洒宽度达到最大。周斌等[15]研究分析了微喷带单孔水量分布与湿润区面积、干燥区宽度、湿润区宽度等各因素之间的关系,发现微喷带喷射角度为40°左右时喷洒宽度最大。尽管国内外对微喷带喷洒宽度有所研究,但均采用试验研究,多是对试验数据进行分析总结,缺少一个适用于微喷带喷洒宽度的理论计算公式。故本文开展微喷带喷洒宽度试验,基于牛顿力学与流体力学理论建立微喷带喷洒水滴运动数学模型,推导微喷带喷洒宽度理论计算公式,确定公式的参数,并对微喷带喷洒宽度理论计算公式影响因素进行分析。
1 材料与方法
1.1 试验材料
通过市场调研,收集了中国农业中常见的6种微喷带,其中微喷带试样的折径、孔径由生产厂家提供,测量出微喷带孔边距、横向孔间距,结合折径利用弧长公式确定出微喷带的喷孔仰角。为便于不同类型的微喷带对比分析,对微喷带式样进行了编号。具体参数见表1。并绘制微喷带结构式样图,如图1所示。

图1 微喷带结构式样图

表1 试验微喷带试样具体参数表
注:NY/T44-0.8-3代表微喷带型号,其中44代表折径,0.8代表喷孔直径,3代表喷孔数。以此类推。
Note: NY/T44-0.8-3 stands for the type of micro-sprinkling hose, of which 44 stands for the folding width, 0.8 stands for the nozzle diameter, and 3 stands for the number of nozzles. And so on.
1.2 试验方案
试验场地选在天津市农业水利技术工程中心试验基地完成。主要开展微喷带水滴直径、喷洒宽度试验。主要的试验设备有水泵、稳压装置、调压闸阀、电磁流量计、精密压力表、堵头、集水桶、量筒、精密天平(精度10-4)、滤纸等。
1)喷洒宽度的测量。根据《农业灌溉设备非旋转式喷头技术要求和试验方法》(GB/T 18687—2012)[16]中规定,喷洒宽度是指测出灌水强度为某数值的那个点距喷头中心线的距离。对于流量等于或小于75 L/h的喷头,该点的喷洒强度为0.13 mm/h。
试验中待测微喷带样本长度选取5 m,有效试验数据取中间2.5 m,以保证消除边界影响。工作压力在0.03~0.06 MPa分4个等级。微喷带正面向上铺设,保证微喷带两侧喷洒均匀。集水桶布置在微喷带一侧,垂直微喷带方向布置5条射线,射线间距50 cm,射线上雨量桶布置间距50 cm。测试时间15 min,用量筒测量集水桶中喷洒水量。每个压力处理试验重复3次。
2)水滴直径的测量。采用改进滤纸法测量水滴直径,首先利用精密天平称滤纸质量,然后用滤纸在沿微喷带喷射水流首端、中部、末端接取水滴[17-19],并迅速利用精密天平再次测量其质量,最后数出滤纸上的水痕数量。由于喷灌蒸发损失较小,所以一般不考虑蒸发损失,将水滴在运动过程中视为球体[20-22],则利用质量差与水滴数求出水滴直径,并将不同部位接取水滴直径平均值作为微喷带水滴直径。每个压力处理试验重复3次。
2 薄壁微喷带喷洒宽度模型建立
2.1 微喷带喷洒水滴受力分析
根据牛顿万有引力定律,水滴重力1为
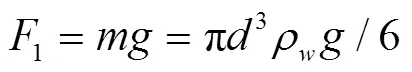
式中为水滴质量,kg;为水滴直径,m;ρ为水的密度,kg/m3;为重力加速度,m/s2。
由于水滴占一定的体积,在空气中将受到浮力作用,则浮力2为

式中ρ为空气的密度,kg/m3。
根据流体力学理论,当运动物体的雷诺数很大时,则阻力与速度的2次方成正比[23]。对于微喷带喷孔喷出的水流,雷诺数较大,所以处于阻力平方区,阻力3可以表示为

式中为水滴摩擦系数;为水滴速度,m/s。
2.2 水滴运动模型的建立及求解
2.2.1 水滴运动方程建立
对水滴在空气中运动所受的力进行分析,根据牛顿第二定律,在垂直于微喷带铺设方向的竖直平面内建立水滴运动方程。
在方向

在方向

初始边界条件
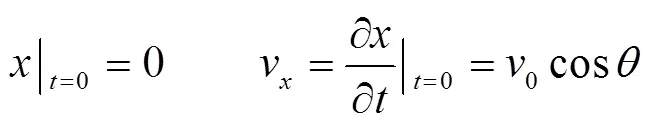
上升时初始条件
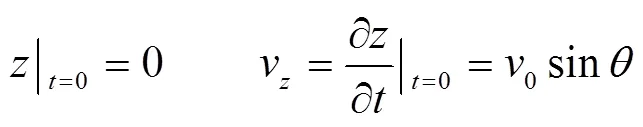
下降时初始条件
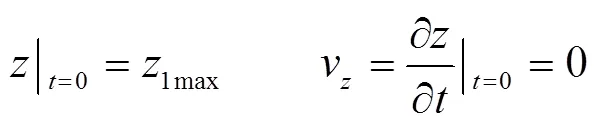
式中为水滴在竖直方向的合加速度,m/s2;v和v为分别为水滴在运动过程中任一时间点时在、轴投影的速度,m/s;0为喷孔出口处水流速度,m/s;为微喷带任一喷孔与水平地面间夹角,(°);1max为上升最大高度,m。
2.2.2 水滴位移公式与总时间求解
1)水平方向运动
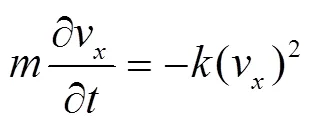
将边界条件式(6)代入式(9),整理并积分可得
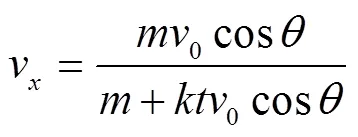
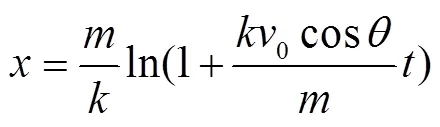
2)竖直方向运动
对水滴进行受力分析可知,在竖直向上与竖直向下时受力不同,引力总是竖直向下,浮力竖直向上,但空气阻力与运动方向相反。所以将竖直方向运动分为竖直向上和竖直向下。
竖直向上时运动方程为


将边界条件式(7)代入公式(13),整理并积分可得

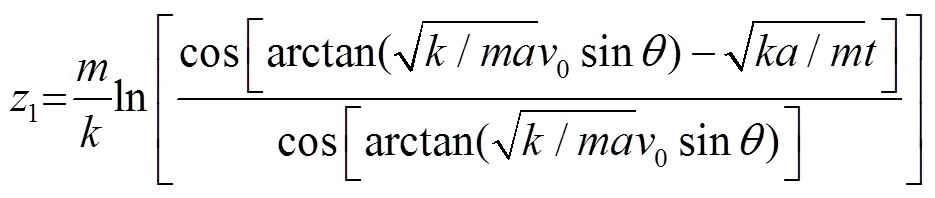
通过分析可知当水滴运动到最高点时,此时速度为0,运动时间为1,将v=0代入式(14)得
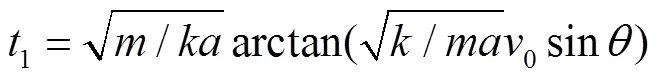
将1代入式(15)最大上升高度1max为
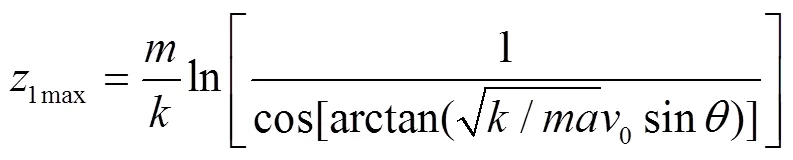
竖直向下时运动方程为
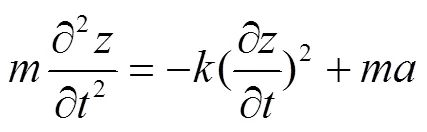
同理,将边界条件式(8)代入得式(18)
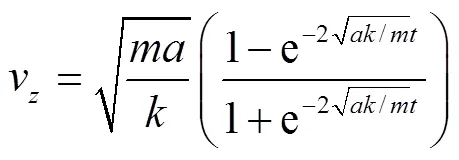

对于水滴下降时,当引力与浮力合力等于阻力时,此时加速度为0,即达到极限速度。由于水滴质量较小,所以下降时很快达到极限速度,此后将以极限速度做匀速运动[13]。为了简化计算,则下降全过程认为是做匀速运动。经分析,极限速度为

时间2可得
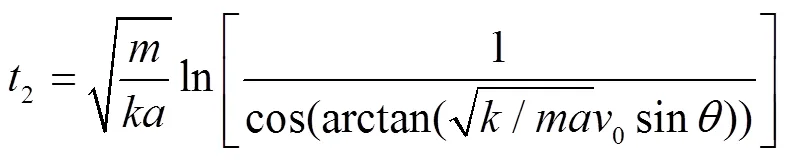
则可知总时间
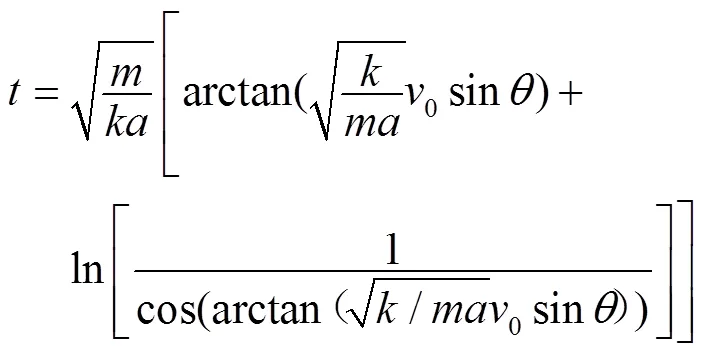
通过前面计算分析,将总时间代入到式(11)即得到微喷带任一喷孔喷洒宽度公式
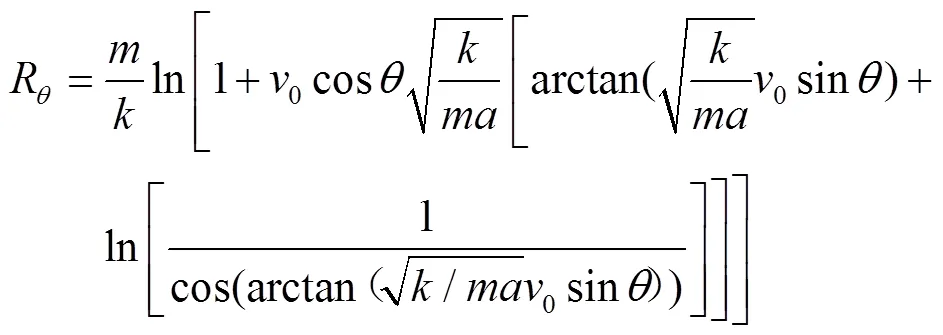
对于同一条微喷带有不同喷孔,就有不同喷孔仰角,对应不同喷洒宽度则取最大喷洒宽度作为微喷带喷洒宽度。则微喷带喷洒宽度为
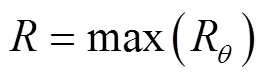
3 薄壁微喷带喷洒宽度公式参数确定
3.1 喷洒水滴直径的确定
水滴直径是指落在地面或者作物叶面上的水滴直径。水滴直径沿着喷洒半径方向呈增加趋势,喷洒半径末端一般出现最大水滴直径[24-27]。试验数据见表2。
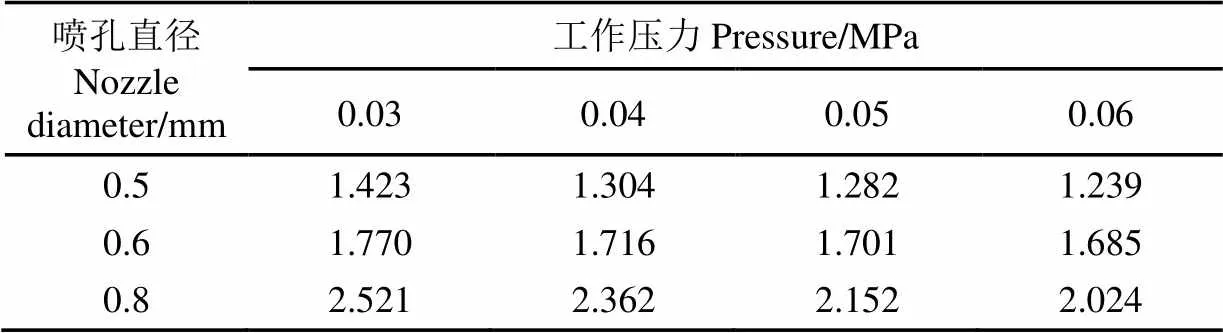
表2 微喷带喷洒水滴直径试验数据
利用软件结合模型利用表2中的数据进行多元线性回归处理。结果显示,模型相关系数平方2=0.962,相伴概率值<0.001,均方根误差RMSE=0.099。经回归拟合后,通过计算推导得出水滴直径计算公式

式中为水滴直径,mm;为喷孔直径,mm;为工作压力,MPa。
3.2 喷洒水滴摩擦系数确定
水滴在空气中运动的摩擦系数的确定公式有很多,本文采用斯托克斯阻力公式得
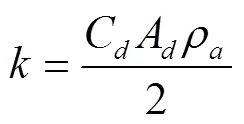
式中C为摩擦阻力系数;A为与水滴运动方向垂直的水滴迎风的投影面积,mm2,A=π24;ρ为空气密度,kg/m3,ρ取1.29 kg/m3。C主要依据喷孔出口的雷诺数来确定,根据文献[28]可知,微喷带喷洒水滴摩擦系数计算中C取0.44。
3.3 喷洒水滴初始流速确定
薄壁微喷带在喷孔处可以近似认为势能全部转化为动能[29],利用能量守恒原理可知微喷带喷孔初始流速
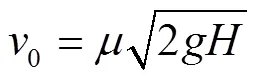
式中0为喷孔水流初始流速,m/s;为工作压力,MPa;为流量系数,对于不同型号微喷带流量系数不同,通过试验测得流量系数取值范围为0.95~0.99,本文取0.97。
3.4 喷洒水滴竖直方向合加速度确定
对喷洒水滴在竖直方向进行受力分析,发现不管在上升过程还是下降过程,重力方向始终向下,浮力始终向上,则合加速度见式(29)。

经计算分析可知,喷洒水滴在空气中受到浮力为重力的千分之一,在计算中可以不考虑空气浮力[30],合加速度,近似等于重力加速度。
4 模型验证与结果分析
4.1 理论计算公式验证
通过推导得出微喷带理论喷洒宽度计算公式,利用理论公式计算同一微喷带试样的不同喷孔仰角喷洒宽度,取最大值作为微喷带喷洒宽度,然后与试验数据进行验证,结果见表3。由表3可知,利用薄壁微喷带喷洒宽度理论计算公式获得结果较为精确。对于6种不同型号微喷带的24组对比结果中,相对误差均小于10%。其中相对误差在5%以内的占比为70.83%,相对误差在5%~10%占比为29.17%。

表3 薄壁微喷带喷洒宽度理论计算结果与试验结果对比
4.2 理论计算公式分析
前面对微喷带喷洒宽度理论计算公式进行详细推导,现对喷洒宽度理论计算公式进行分析。公式适用于任何型号微喷带,为了直观反映微喷带喷洒宽度影响因素,以NY/T63-0.6-7为例,在同一工作压力、喷射仰角下分析不同喷孔直径下的微喷带喷洒宽度(图2a);在同一喷射仰角、喷孔直径下分析不同工作压力下的微喷带喷洒宽度(图2b);在同一工作压力、喷孔直径下分析不同喷射仰角下的微喷带喷洒宽度(图2c)。通过分析图2与表3可知,对于同一工作压力、同一喷孔仰角,喷洒宽度随喷孔直径增加而增加;对于同一喷孔直径、同一喷孔仰角微喷带,喷洒宽度随着工作压力增加而增加,且增加速率逐渐减小;对于同一工作压力、喷孔直径下,微喷带喷洒宽度随着喷孔仰角增加呈先增加后减小的变化趋势,且变化速率先减小后增加,且在40°左右取得最大值。
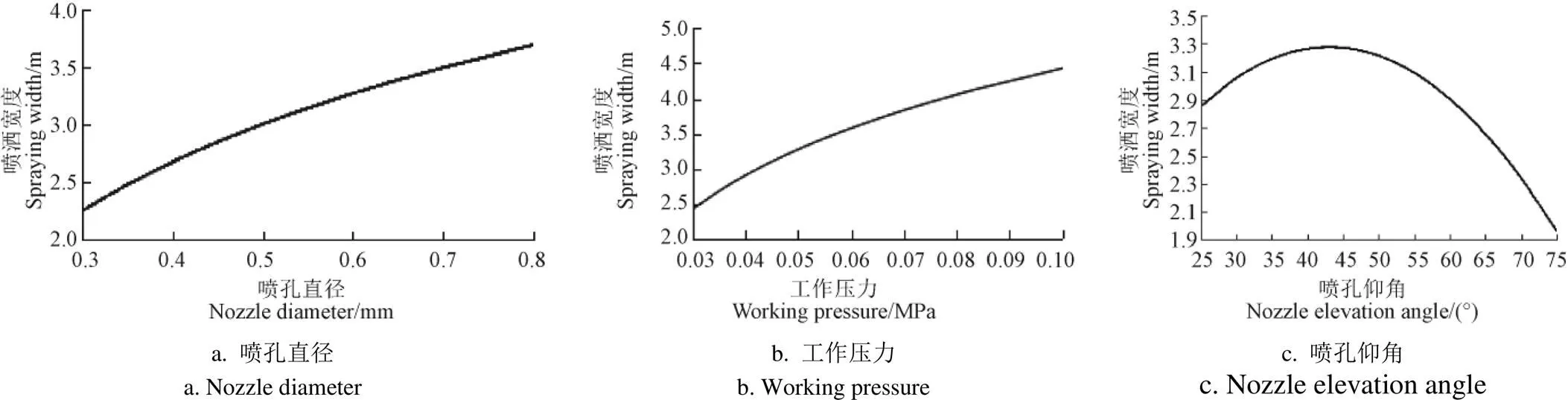
注:图2a中工作压力为0.05 MPa,喷孔仰角为31.43°;图2b中喷孔仰角为31.43°,喷孔直径为0.6 mm;图2c中工作压力为0.05 MPa,喷孔直径为0.6 mm。
5 结 论
本文通过开展薄壁微喷带喷洒水滴直径试验与喷洒宽度试验,推导了微喷带喷洒宽度理论计算公式,该公式能够为微喷带生产厂家提供一定设计依据,为微喷带田间布设提供一定理论依据。具体结论如下:
1)微喷带喷洒水滴直径试验表明,微喷带喷洒水滴直径与喷孔直径呈负相关,与工作压力呈正相关,工作压力越大,喷洒水滴直径越小。
2)通过开展微喷带喷洒宽度试验,利用牛顿力学与流体力学理论,考虑喷洒水滴在空气中受到重力、浮力与空气阻力,建立了微喷带喷洒水滴运动模型,推导了微喷带喷洒宽度理论计算公式。利用实测数据对微喷带喷洒宽度理论公式进行验证,结果表明理论计算公式与实测值吻合程度较好,误差均小于10%,可以广泛应用于微喷带喷洒宽度计算。
3)对喷洒宽度计算公式进行影响因素分析可知,微喷带喷洒宽度随喷孔仰角增加呈先增加后减小,且在40°附近时喷洒宽度取得最大值;在一定工作压力范围内,喷洒宽度与工作压力呈正相关;在一定喷孔直径范围内,喷洒宽度与喷孔直径呈正相关。
[1] 董志强,张丽华,李谦,等. 微喷灌模式下冬小麦产量和水分利用特性[J]. 作物学报,2016,42(5):725-733. Dong Zhiqiang, Zhang Lihua, Li Qian, et al. Grain yield and water use characteristics of winter wheat under micro-sprinkler irrigation[J]. Acta Agronomica Sinica, 2016, 42(5): 725-733. (in Chinese with English abstract)
[2] 徐袁博. 不同微喷带布置间距与灌水量对冬小麦的影响[D]. 杨凌:西北农林科技大学,2017. Xu Yuanbo. The Effect of Different Spacing of Micro-Sprinkling Hose and Irrigation Amount on Winter Wheat[D]. Yangling: Northwest A&F University, 2017. (in Chinese with English abstract)
[3] 袁寿其,李红,王新坤. 中国节水灌溉装备发展现状、问题、趋势与建议[J]. 排灌机械工程学报,2015,33(1):78-92. Yuan Shouqi, Li Hong, Wang Xinkun. Status, problems, trends and suggestions for water-saving irrigation equipment in China[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(1): 78-92. (in Chinese with English abstract)
[4] 李敬库. 微喷带灌溉技术研究及应用进展[J]. 东北水利水电,2017,35(1):53-56. Li Jingku. Progress in research and application of micro-spray irrigation technology[J]. Water Resources & Hydropower of Northeast China, 2017, 35(1): 53-56. (in Chinese with English abstract)
[5] 张学军,吴政文,丁小明. 微喷带水量分布特性试验分析[J].农业工程学报,2009,25(4):66-69. Zhang Xuejun, Wu Zhengwen, Ding Xiaoming, et al. Experimental analysis of water distribution characteristics of micro-sprinkling hose[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(4): 66-69. (in Chinese with English abstract)
[6] 张硕. 微喷带水力性能及水量分布试验研究[D]. 杨凌:西北农林科技大学,2017. Zhang Shuo. Experimental Study on Hydraulic Performance and Water Distribution of Micro Jet[D]. Yangling: Northwest A&F University, 2017. (in Chinese with English abstract)
[7] 程维国. 微喷灌技术在大田作物中的应用[J]. 北京农业,2013(27):175. Cheng Weiguo. Application of micro sprinkler irrigation technology in field crops[J]. Beijing Agriculture, 2013(27): 175. (in Chinese with English abstract)
[8] 苟万里,杨路华,邸志刚,等. 薄壁微喷带沿程水头损失试验研究[J]. 灌溉排水学报,2019,38(5):79-83. Gou Wanli, Yang Luhua, Di Zhigang, et al. Experimental study on water head loss along thin-wall spray-irrigation pipe[J]. Journal of Irrigation and Drainage, 2019, 38(5): 79-83. (in Chinese with English abstract)
[9] 王凤民,张丽媛. 微喷灌技术在设施农业中的应用[J]. 地下水,2009,31(6):115-116. Wang Fengmin, Zhang Liyuan. Application of micro sprinkler irrigation technology in facility agriculture[J]. Ground Water, 2009, 31(6): 115-116. (in Chinese with English abstract)
[10] 中华人民共和国国家质量监督检验检疫总局. 微灌工程技术规范:GB/T50485-2009[S]. 北京:中国标准出版社,2009.
[11] Deboer D W, Monnens M J. Estimation of drop size and kinetic energy from a rotating-plate sprinkler[J]. Transactions of ASAE, 2001, 44(6): 1571-1580.
[12] Sayyadi H, Gazemi A H, Sadraddini A. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler[J]. Biosystems Engineering, 2014, 119: 13-24
[13] 脱云飞,杨路华,柴春岭,等. 喷头射程理论公式与试验研究[J]. 农业工程学报,2006,22(1):23-26. Tuo Yunfei, Yang Luhua, Chai Chunling, et al. Experimental study and theoretical formula of the sprinkler range[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(1): 23-26. (in Chinese with English abstract)
[14] 王建军,杨筠晴,蔡九茂,等. 工作压力及喷射角度对微喷带单孔喷水特性影响的试验研究[J]. 节水灌溉,2018(3):35-38. Wang Jianjun, Yang Yunqing, Cai Jiumao, et al. Experimental study on the influence of working pressure and spraying angle on the single-hole spray characteristics of micro-sprinkling hose[J]. Water Saving Irrigation, 2018(3): 35-38. (in Chinese with English abstract)
[15] 周斌,封俊,张学军,等. 微喷带单孔喷水量分布的基本特征研究[J]. 农业工程学报,2003,19(4):101-103. Zhou Bin, Feng Jun, Zhang Xuejun, et al. Characteristics and indexes of water distribution of punched thin-soft tape for spray[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(4): 101-103. (in Chinese with English abstract)
[16] 中华人民共和国国家质量监督检验检疫总局. 农业灌溉设备-非旋转式喷头技术要求和试验方法:GB/T 18687—2012[S]. 北京:中国标准出版社,2013.
[17] 张林,惠鑫,陈俊英. 坡地喷灌水滴直径与动能强度分布规律研究[J]. 农业机械学报,2018,49(6):263-270. Zhang Lin, Hui Xin, Chen Junying. Droplet diameter and kinetic energy intensity distribution regularities for sprinkler irrigation on sloping land[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(6): 263-270. (in Chinese with English abstract)
[18] 刘兴发. 全射流喷头水滴分布特性试验研究[D]. 镇江:江苏大学,2016. Liu Xingfa. Droplets Distribution Characteristic Study on Complete Fluidic Sprinkler[D]. Zhenjiang: Jiangsu University, 2016. (in Chinese with English abstract)
[19] 徐红,龚时宏,贾瑞卿,等. 新型ZY系列摇臂旋转式喷头水滴直径分布规律的试验研究[J]. 水利学报,2010,41(12):1416-1422. Xu Hong, Gong Shihon, Jia Ruiqing, et al. Study ondroplet size distribution of ZY sprinkler head[J]. Journal of Hydraulic Engineering, 2010, 41(12): 1416-1422. (in Chinese with English abstract)
[20] Lima D, Torfs J F, Singh V P. A mathematical model for evaluating the effect of wind on downward spraying rainfall simu-lators[J]. Catena, 2001, 46(4): 221-241.
[21] Heermann D F, Kohl R A. Fluid Dynamics of Sprinkler Systems[M]∥Jensen M E. Design and Operation of Farm Irrigation Systems. Michigan: ASAE, 1980: 583-618.
[22] 黄修桥. 有风时的喷洒水滴运动规律及风对喷头射程的影响[J]. 灌溉排水学报, 1992,11(2):1-7. Huang Xiuqiao. Moving of spray droplet under wind condition and the effect of wind on spray distance of nozzle[J]. Journal of Irrigation and Drainage, 1992, 11(2): 1-7. (in Chinese with English abstract)
[23] 汪志明. 流体力学[M]. 北京:石油工业出版社,2006.
[24] 刘海军,龚时宏. 喷灌水滴的蒸发研究[J]. 节水灌溉,2000(2):16-19. Liu Haijun, Gong Shihong. Study on evaporation of sprinkler droplets[J]. Water Saving Irrigation, 2000(2): 16-19. (in Chinese with English abstract)
[25] 朱兴业,刘兴发,刘俊萍,等. 基于LPM的摇臂式喷头水滴分布试验研究[J]. 排灌机械工程学报,2015,33(10):908-914. Zhu Xingye, Liu Xingfa, Liu Junping, et al. Droplets distribution research of impact sprinkler based on Laser precipitation monitor[J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(10): 908-914. (in Chinese with English abstract)
[26] 严海军,肖建伟,李文颖,等. 圆形喷灌机低压阻尼喷头水滴直径分布规律的试验研究[J]. 水利学报,2014,45(4):467-473. Yan Haijun, Xiao Jianwei, Li Wenying, et al. Droplet size distribution of low-press damping sprinklers used in center-pivot irrigation systems[J]. Journal of Hydraulic Engineering, 2014, 45(4): 467-473. (in Chinese with English abstract)
[27] 白更,严海军. 空气阻力系数对水滴运动及蒸发的影响[J]. 水利学报,2011,42(4):448-453. Bai Geng, Yan Haijun. Effect of air drag coefficient on motion and evaporation of water droplet[J]. Journal of Hydraulic Engineering, 2011, 42(4): 448-453. (in Chinese with English abstract)
[28] 崔谟慎,孙家骏. 高压水射流技术[M]. 北京:煤炭工业出版社,1993.
[29] 郑迎春. 微喷带水力性能试验研究[D]. 保定:河北农业大学,2009. Zheng Yingchun. Experimental Study on Hydraulic Characteristics of Micro-Spraying Hose[D]. Baoding: Agricultural University of Hebei, 2009. (in Chinese with English abstract)
[30] 王波雷,马孝义,范严伟,等. 旋转式喷头射程的理论计算模型[J]. 农业机械学报,2008,39(1):41-45. Wang Bolei, Ma Xiaoyi, Fan Yanwei, et al. Modeling and experiment validation on the rotational sprinkler nozzle range[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(1): 41-45. (in Chinese with English abstract)
Model establishment of spraying width of thin-walled micro-sprinkling hose
Di Zhigang1,2, Yang Luhua1※, Gou Wanli1, Wang Jinyi1
(1.,,300384,; 2.,,100053,)
China is the biggest agricultural production country in the world and the agriculture is related to its stability and development. With the development in water-saving irrigation technology, micro-sprinkling hose has been widely promoted and applied in China in recent years as an improved equipment duo to its efficiency in water-saving. To facilitate production and upgrading, as well as guide planning and design of the micro-sprinkling hose in irrigation, we experimentally studied the spray width in the hose at Tianjin Agricultural Water Saving Technology Engineering Center (39°N, 116°E). After literature review and market research, we selected six common micro-sprinkling hoses available in the market, and measured and calculated their folding width, nozzle diameter and nozzle elevation angle in the spray width test. The length of the sample in the test was 5 m and the working pressure varied from 0.03 to 0.06 MPa. The micro-sprinkling hose was laid at the upfront to ensure uniform spraying on both sides of the hose. The water collecting bucket was on one side of the hose and five rays spaced 50 cm were arranged in the vertical direction of the hose, with the collecting bucket on the ray spaced 50 cm. At the end of the experiment, the amount of water in the bucket was measured and the spraying width was determined. In the meantime, we also measured the diameter of the spraying droplets using filter paper method. The quality of the paper was measured by a precision balance, and the water droplets were connected to the paper at the head, middle and end of the spray stream along the hose. The quality of the paper was measured again quickly by the precision balance prior to counting the number of water marks on it, which, along with mass balance, was used to calculate the diameter of the water droplets. The average diameter of the water droplets at different locations was taken as the diameter of the water droplets in the hose. Considering the factors such as air resistance, gravity and buoyancy that act on the water droplets, a model for water droplet moving in the hose was proposed based on the Newtonian fluid mechanics. We also derived a formula for the spray width, determined the parameters in the formula, validated them against experimental data, and analyzed the factors that affect the accuracy of the formula. The results show that the derived formula for spray width in the hose agreed well with both analytical values and experiment data, and, compared with the experimental data, its relative error for the six selected hoses was less than 10%. Both the experimental data and theoretical analysis of the formula reveal that the spray width in the hose increases with the elevation angle of the nozzle before declining after it peaked when the nozzle elevation angle was approximately 40°. The spray width increases with both working pressure and nozzle diameter within certain ranges. It was also found that the derived formula was accurate and can be used to calculate the spray width, offering a theoretical tool for planning and designing micro-sprinkling hose irrigation system.
irrigation; flow; model; micro-sprinkling hose; spray width; working pressure; nozzle diameter; nozzle elevation angle
2019-04-14
2019-07-10
水利部海河水利委员会资助项目(TNHP2018001)
邸志刚,研究方向为节水灌溉理论与技术。Email:562610819@qq.com
杨路华,博士,教授,研究方向为农业节水灌溉理论与技术。Email:yangluhua@tjau.edu.cn
10.11975/ j.issn.1002-6819.2019.17.004
S275.5
A
1002-6819(2019)-17-0028-07
邸志刚,杨路华,苟万里,王金毅. 薄壁微喷带喷洒宽度模型构建[J]. 农业工程学报,2019,35(17):28-34. doi:10.11975/ j.issn.1002-6819.2019.17.004 http://www.tcsae.org
Di Zhigang, Yang Luhua, Gou Wanli, Wang Jinyi. Model establishment of spraying width of thin-walled micro-sprinkling hose[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(17): 28-34. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.17.004 http://www.tcsae.org

