一类具有常数输入和马氏转换的SIQRS模型

赵晓静, 张 龙, 张德婷

(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)

0 引言及模型建立

近年来,传染病动力学发展迅速,人们建立了大量的流行病模型,如SIS、SIRS、 SIER和SIQR等,并取得了很多重要结果[1].在传染病模型中,发病率函数对于环境波动的影响最为敏感,因此它扮演着1个关键性的角色,确保模型能合理地描述疾病流行的动态[2].一般地,都假设疾病传播的发生率为双线型,即βSI，如文献[3]建立了具有隔离项和双线性疾病发生率的SIQR模型

(1)

但事实上,1个人的传染力是有限的,所以考虑饱和发生率更符合实际,也更有意义.此外,上述模型并没有考虑外界环境的随机影响.在实际生活中,疾病所处的环境因素并不是一成不变的,不同环境中疾病的表现也不同.比如说,在比较潮湿的紫外线较低的环境中,疾病的存活性和传染性更强,而在紫外线较高的干燥环境中,存活性和传染性较差[4-6].种群的增长率和环境的容纳量会随食物资源的丰度变化而有所不同,因为食物资源的丰度在很大程度上依赖于不可预知的降水等问题[7],因此,很多研究学家开始关注这一现象.Gray等[8]首先提出用带有马氏转换的传染病模型来进行刻画,并得到了一些很好的结论.关于马尔克夫转换的传染病模型,Li等[9]已经做出了很好的总结.国内外学者虽然对随机传染病模型的研究有了一定的成就,但对于带有马氏转换的SIQRS模型研究却较少.因此研究带有马氏转换且疾病发生率为饱和的SIQRS传染病模型是很有实际意义的.

由此,建立了SIQRS传染病模型

(2)

其中,S(t)代表易感者类,I(t)代表普通染病者类,Q(t)代表染病隔离者类,R(t)代表移除者类,总人口数为N(t)=S(t)+I(t)+Q(t)+R(t).Λ代表新增易感者人数,μ代表人均自然死亡率系数,α代表因病死亡率系数,δ代表隔离率系数,γ和ε代表普通染病者和染病隔离者的恢复率系数,λ表示免疫消失率系数.疾病传播率系数β由时齐马氏链{r(t),t≥0}表示,r(t)在有限的状态空间Μ={1,2,…,E}中取值,表示不同的环境.

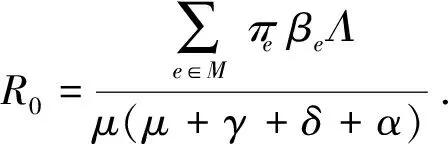
1 预备知识

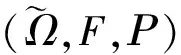
在本文中,做如下假设:

(H)g(x)在[0,Λ/μ]满足Lipschitz性质,即存在常数θ>0,使得对任意x1,x2∈[0,Λ/μ],满足

|g(x1)-g(x2)|≤θ|x1-x2|,

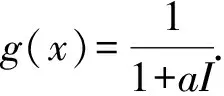
为研究系统的动力学,需要引入下面的引理.

引理 1若x*∈R4是系统

的1个全局渐进稳定的平衡点,则对x*的任意邻域U和任意紧集C⊂R4,存在T>0,使得对所有t≥T和x0∈C有x(t,x0)∈U成立.

2 主要结果

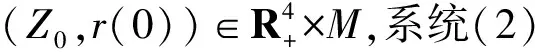
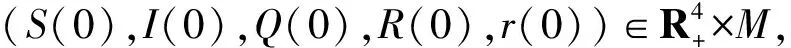
下证此解具有全局性,则只需证明τe=∞a.s.,令k0≥1充分大使得S(0),I(0),Q(0),R(0)∈[1/k0,k0].记inf ∅=∞(∅代表空集).对任意k≥k0,定义停时

τk={t∈[0,τe) :min{S(t),I(t),Q(t),R(t)}≤

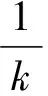
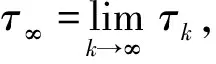
Ρ{τ∞≤T}>ε.

故存在整数k1≥k0,使得

Ρ{τk≤T}≥ε,k≥k1.

(3)

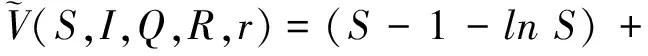
(I-1-lnI)+(Q-1-lnQ)+(R-1-lnR).

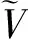
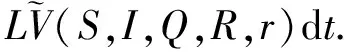
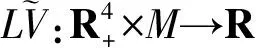
Λ-μ(S+I+Q+R)+4μ+

其中K为正常数,且与S、I、Q、R、e无关,因此有

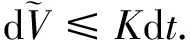
(4)

对(4)式从0到τk∧T积分并取期望得

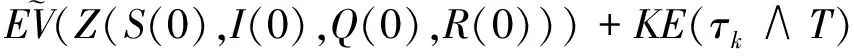
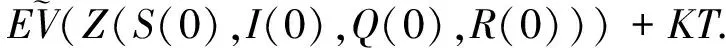
(5)

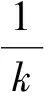
则有

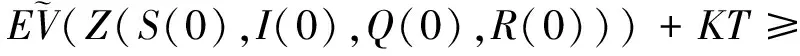
其中,IΩk表示Ωk的示性函数.令k→∞,则有

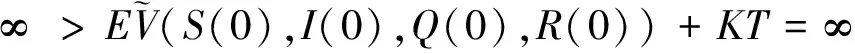
矛盾,所以τ∞=∞ a.s..故τe=∞ a.s..

令N=S+I+Q+R,则

(μ+γ+δ+α)I+δI-(μ+η+α)Q+γI+ηQ-

(μ+λ)R=Λ-μ(S+I+Q+R)-α(I+Q),

所以

由常数变易公式计算得

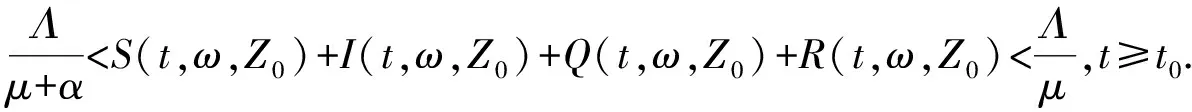
命题 3对R0值的以下替代条件成立:

由于这个定理的证明可以直接得出,故这里省略.

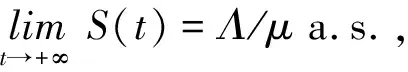
(6)

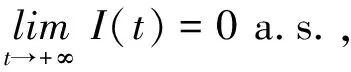
(7)

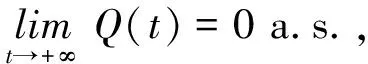
(8)

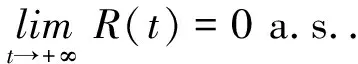
(9)

证明第一步,证明(7)式成立.由系统(2)的第二个方程知

则

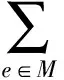
由命题3的(i)知

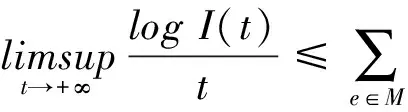
故

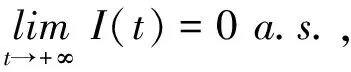
即(7)式成立.

第二步,证明(8)式成立.

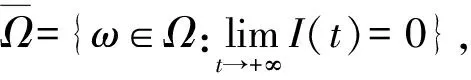
由比较原理知

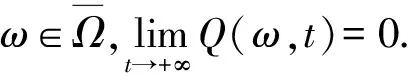
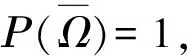
第三步,证明(9)式成立.

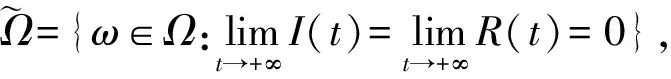
由比较原理知

同理第二步可得

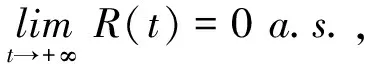
即(9)式成立.

第四步,证明(6)式成立.

令N(t)=S(t)+I(t)+Q(t)+R(t),由系统(2)可知

解得

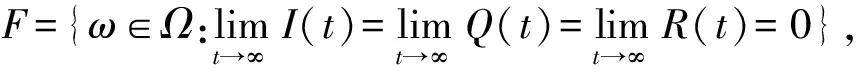
所以

由ε3的任意性知

另一方面,由引理2知

所以

故得

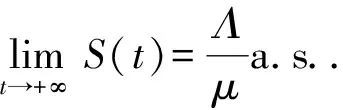
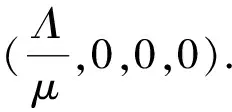
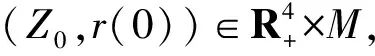
证明由系统(2)的第二个方程知

则

对上式两边积分得

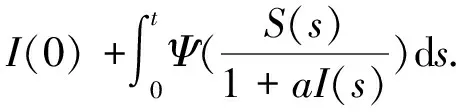
(10)

又因为

所以

将上式代入到(10)式得

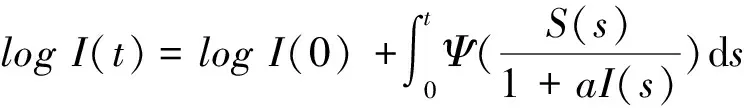
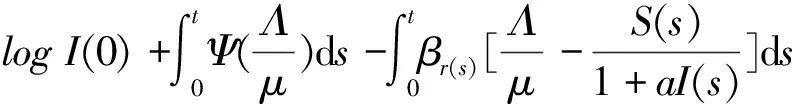
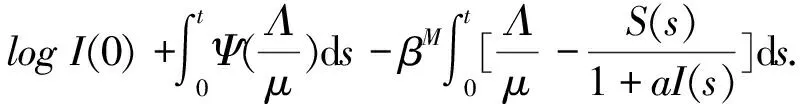
由系统的第一个方程知

对上述不等式两边积分得

故

(12)

将(12)式代入到(11)式得

所以

证毕.

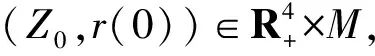
推论 6对任意初值(Z0,r(0))∈X,系统的解(S(t),I(t),Q(t),R(t)),满足:

(i) 若R0<1,则系统(2)的染病者的数目将几乎确定指数收敛于0的概率为1;

(ii) 若R0>1,则疾病几乎确定持久.

3 数值模拟

在本节中，对系统(2)进行数值模拟，令M={1,2},Λ=1.3,μ=0.046,λ=0.027,a=0.001 3,γ=0.004 6,δ=0.452 0,α=0.003 5,η=0.008,且这些参数保持不变.为方便对比,设S(0)、I(0)、Q(0)和R(0)在状态1和状态2的初始值相同,即S(0)=40,I(0)=10,Q(0)=5,R(0)=5.在状态1,β1=0.038,相对应的基本再生数R1=2.122 0>1,此时,S(t)、I(t)、Q(t)和R(t)随时间t的变化如图1所示,疾病持久.在状态2,β2=0.012,相对应的基本再生数R2=0.670 1<1,此时,S(t)、I(t)、Q(t)和R(t)随时间t的变化如图2所示,疾病消失.

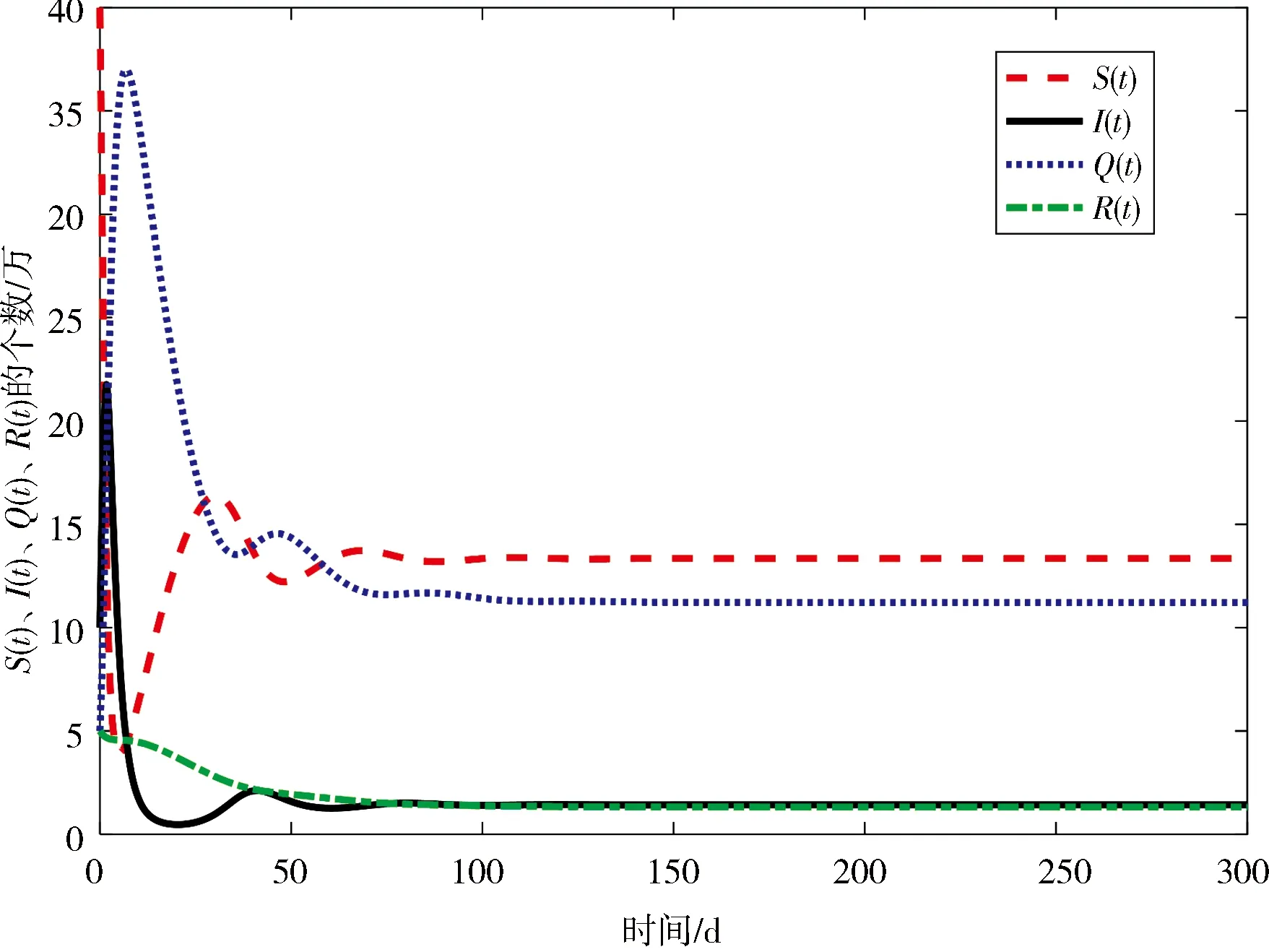
图 1 S(t)、I(t)、Q(t)和R(t)在β1=0.038时的时间序列图

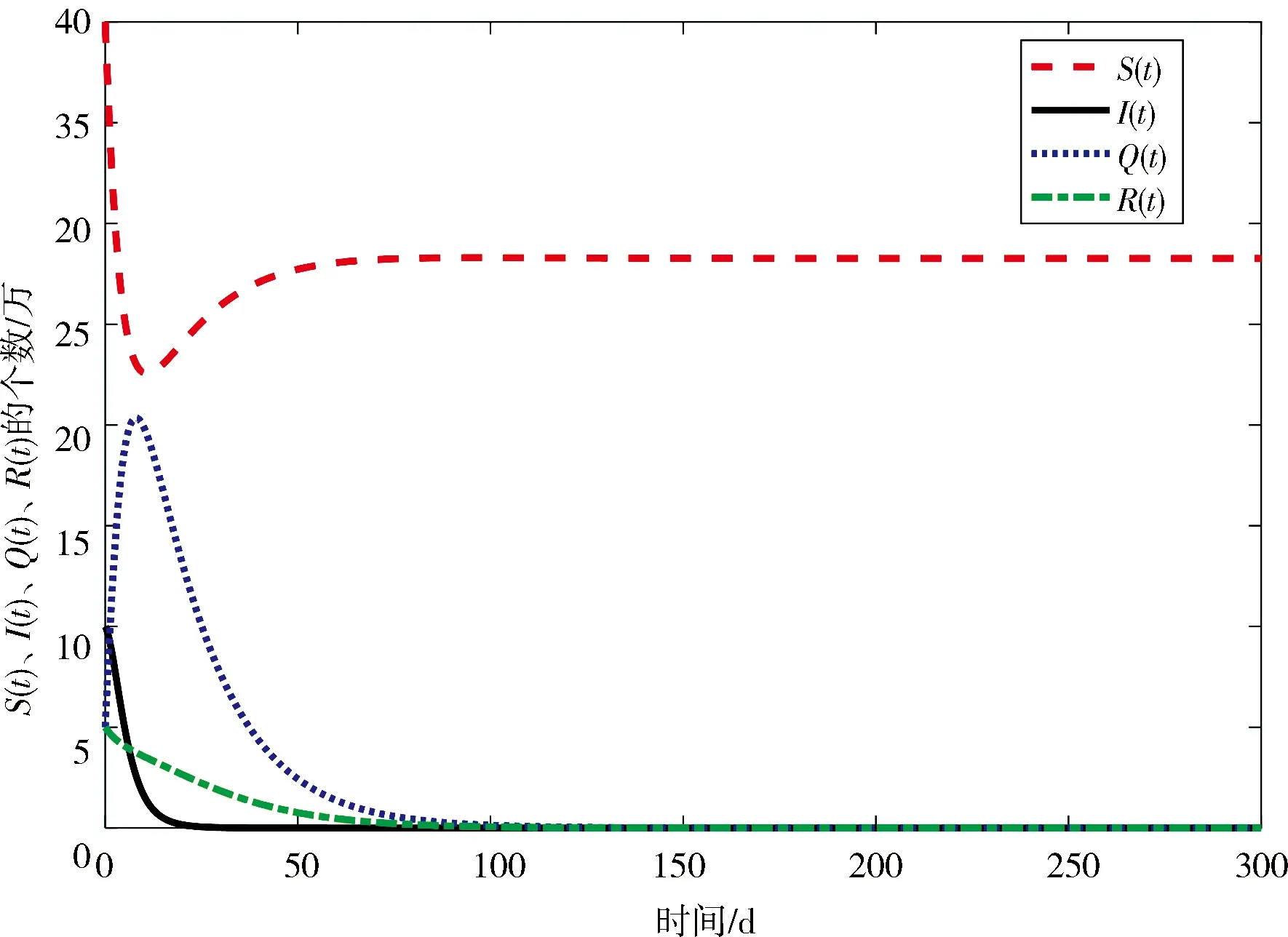
图 2S(t)、I(t)、Q(t)和R(t)在β2=0.012时的时间序列图

Fig.2ThetimeseriesdiagramofS(t),I(t),Q(t),R(t)atβ2=0.012

若取Π=(π1,π2)=(0.5,0.5),对应的R0=1.396 1>1,S(t),I(t),Q(t),R(t)在状态1和状态2之间随时间t的变化如图3所示,疾病随机持久.若取Π=(π1,π2)=(0.2,0.8),则对应的R0=0.960 5<1,S(t),I(t),Q(t),R(t)在状态1和状态2之间随时间t的变化如图4所示,疾病随机消除.

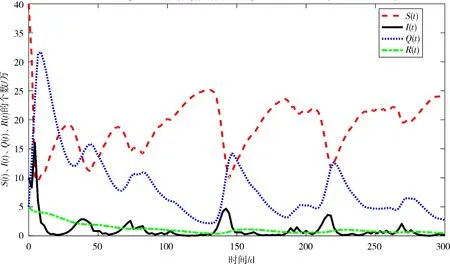
图 3 S(t)、I(t)、Q(t)和R(t)在β1=0.038和β2=0.012之间随机切换下的时间序列图

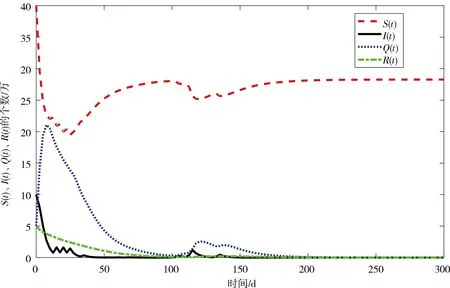
图 4 S(t)、I(t)、Q(t)和R(t)在β1=0.038和β2=0.012之间随机切换下的时间序列图

致谢新疆大学博士科研启动基金(BS160204)、新疆大学博士创新项目(XJUBSCX-2017005) 和自治区普通高等学校科研计划项目(XJEDU2017T001)对本文给予了资助，谨致谢意.