不同土-水特征参数对边坡稳定性影响分析

邢精连，侯 丽，张天琦

(南京市水利规划设计院股份有限公司，江苏 南京 210000)

降雨是导致滑坡的重要因素之一[1- 2]，针对降雨下的边坡渗透特性及稳定性规律，国内外研究较多：荣冠[3]基于饱和非饱和的入渗理论，对强降雨下的元磨公路典型工程边坡渗透稳定性规律进行了研究；王建明[4]考虑了爆破与降雨的综合效应，对含裂纹边坡进行了稳定性数值模拟；余培杰[5]采用数值模拟的手段对露天矿边坡在降雨条件下的渗流稳定规律进行了探讨；肖耀廷[6]基于水文模型推测了边坡所处地区的年降雨分布，以此为基础预测了边坡的稳定性规律；杨智勇[7]对土质边坡的分区域失效概率进行了综合考虑。但是以上研究均未涉及到考虑不同土-水特征曲线下的边坡稳定性规律，事实上，不同的土-水特征参数对边坡稳定性的影响巨大[8- 15]，但是，鲜有对降雨条件下的不同土-水特征曲线敏感性分析的案例报道较少。

本文基于非饱和渗流原理，对不同土-水特征参数下的降雨边坡渗流规律及稳定性规律进行了数值模拟，得到了边坡内部不同监测点的孔压i变化规律及安全系数分布，研究结果为正确认识不同土-水特征参数下的边坡渗透稳定性规律提供了思路。

1 计算理论

1.1 非饱和降雨渗流理论

降雨入渗下，边坡土体的渗流遵循以下方程：

(1)

1.2 边坡安全系数公式

非饱和土的抗剪强度理论采用 Fredlund & Xing[11- 15]提出的抗剪强度公式：

s=c′+σntanφ′+(ua-uw)tanφb

(2)

式中，s—非饱和土的抗剪强度；σn—正应力；c′—有效粘聚力；φ’—有效内摩擦角；φb—材料属性；ua—孔隙气压力；uw—孔隙水压力。

2 计算模型

计算模型如图1所示，设置上部与下部监测点实时监测边坡内部不同点的孔压变化。边坡高度hf=14m，坡脚高度ac=7m，坡比为1∶2，初始条件为图1所示的初始水位线计算所得的初始渗流场作为整个计算模型的初始条件，边界条件设置如下：cdef为降雨入渗边界；cb，gf，ah为不透水边界，ab，gh为定水头边界，分别为3m与8m。整个模型共划分为1347个节点，1552个单元。

图1 计算模型及网格

材料的基础参数如下：饱和体积含水量θs为10%，重度γ为18.6kN/m3，黏聚力c为22kPa，内摩擦角φ为16°，φb为20°。非饱和参数a，m，n，k基础参数取为a=10kPa，m=1，n=4，k=0.01m/d，相应的计算工况为改变土体非饱和参数k，a，m，n，计算边坡的渗透稳定性，降雨强度取为0.01m/d，降雨持续时间取为10d，考虑停雨10d的情况，相应工况如表1所示。

表1 计算工况

3 计算结果

3.1 监测点孔压

不同土-水特征参数下的不同监测点孔压如图2—3所示。

图2 上部监测点孔压变化规律

由图可知，上部监测点孔压随时间呈现在降雨时迅速增大，而在降雨结束时刻缓慢减小的趋势，而下部监测点孔压则呈现在降雨时刻迅速增大，而在降雨结束时刻缓慢增大的趋势，原因是下部监测点的孔压受到上部边坡的雨水排泄作用，使得下部监测点的孔压在降雨结束时刻难以下降。对于上部监测点，参数a与参数m和孔压上升的幅度呈正相关，而参数n与参数k越大，在降雨时上升越快，在降雨结束后下降也越快。对于下部监测点来说，参数m，n与孔压上升的幅度呈正相关，参数a越大，孔压增幅缺越小，但是在参数a=40kPa时却有一个突然的上升，参数k越大，前期孔压上升幅度也越大，而在降雨结束后孔压下降也越快。

3.2 安全系数变化

不同工况下的边坡安全系数的变化规律如图4所示。

由图可知，不同工况下的安全系数呈现在降雨时迅速下降，而停雨后缓慢下降的趋势。参数a越大，整体安全系数越大，但是当a=40kPa时整体安全系数有一个突然的陡降；参数m，n，k越大，安全系数整体上也越大。参数k在降雨前期安全系数几乎一致，而在降雨后期安全系数则随着渗透系数k 的增大而减小。

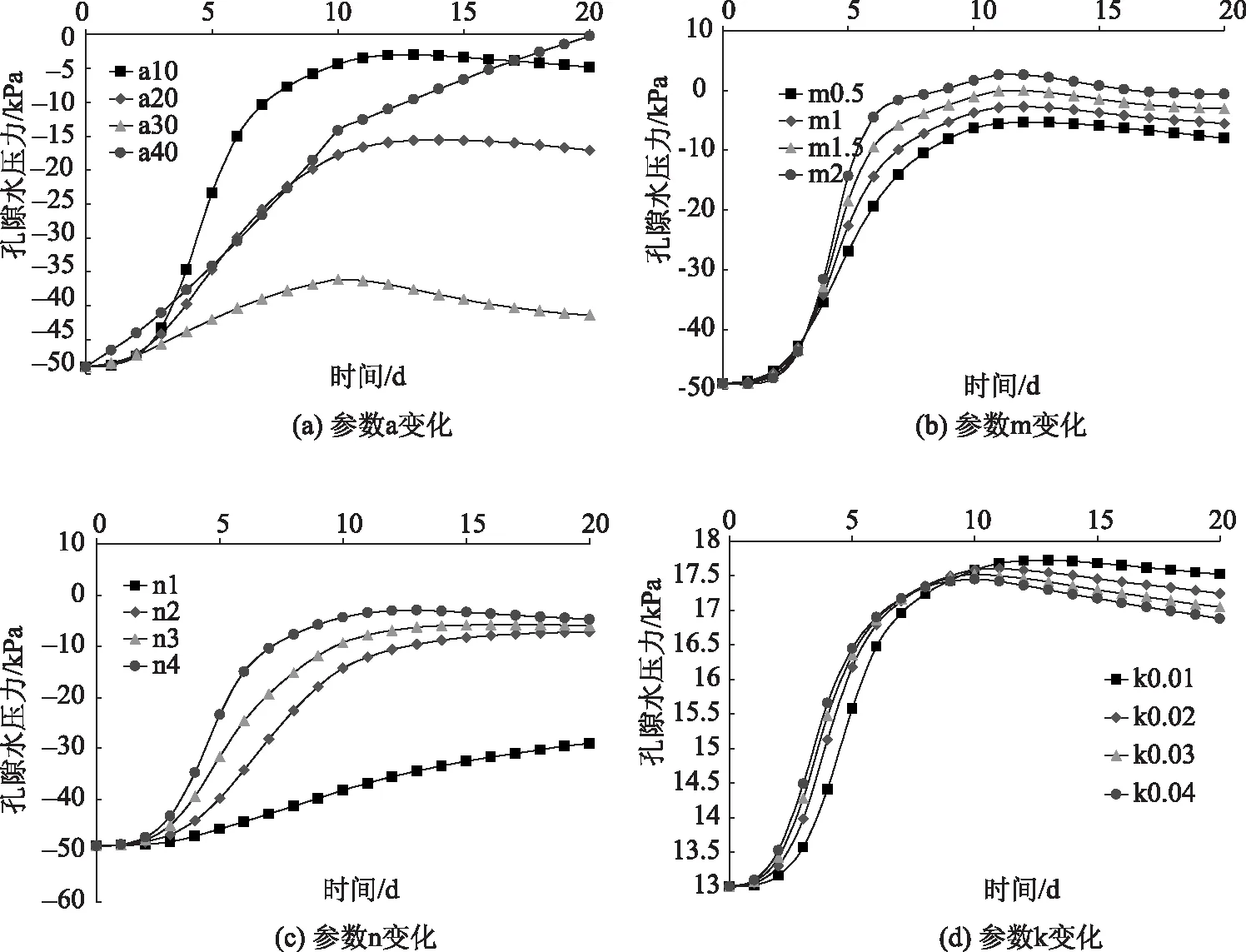
图3 下部监测点孔压变化

图4 安全系数变化规律

4 结论

(1)上部监测点孔压随时间呈现在降雨时迅速增大，而在降雨结束时刻缓慢减小的趋势，参数a与参数m和孔压上升的幅度呈正相关，而参数n与参数k越大，在降雨时上升越快，在降雨结束后下降也越快。

(2)下部监测点孔压则呈现在降雨时刻迅速增大，而在降雨结束时刻缓慢增大，参数m，n与孔压上升的幅度呈正相关，参数a越大，孔压增幅缺越小，但是在参数a=40kPa时却有一个突然的上升，参数k越大，前期孔压上升幅度也越大，而在降雨结束后孔压下降也越快。

(3)不同工况下的安全系数呈现在降雨时迅速下降，而停雨后缓慢下降的趋势。参数a越大，整体安全系数越大，但是当a=40kPa时整体安全系数有一个突然的陡降；参数m，n，k越大，安全系数整体上也越大。参数k在降雨前期安全系数几乎一致，而在降雨后期安全系数则随着渗透系数k 的增大而减小。