基于区间值t-可表示三角范数的模糊推理五蕴涵算法

王雅婧,罗敏霞,张花荣

(中国计量大学 理学院,浙江 杭州 310018)

模糊推理包括许多重要推理方法, 目的是模仿人类思维的推理机制。在模糊推理中,最基本的模型是模糊假言推理(Fuzzy modus ponens, FMP)和模糊反驳推理(Fuzzy modus tollens, FMT):

FMP模型:给定规则A→B,输入A*,输出B*；

FMT模型:给定规则A→B,输入B*,输出A*。

ZADEH在文献[1-2]中提出的合成推理规则(CRI)可以用来解决FMP问题,

其中T是任意的三角范数,I是任意的模糊蕴涵。因为模糊连接词的选取具有任意性,所以CRI算法缺乏严格的逻辑基础,因此,WANG在文献[3]中给出了模糊推理全蕴涵算法(三I算法),

其中R是由左连续三角范数T诱导的剩余蕴涵。三I算法的提出不仅克服了CRI算法的缺陷,而且在文献[4]中将三I算法归纳到了模糊逻辑的框架中。PEI在文献[5]中给出了统一的基于左连续三角范数的三I算法,文献[6]将三I算法与BL和MTL相结合,将三I算法形式化。LUO在文献[7]中选取一类更符合实际的三角范数簇,讨论了基于Schweizer-Sklar剩余蕴涵簇的三I算法及其连续性。文献[8]研究了基于左连续伪三角范数诱导的剩余蕴涵的三I算法的一个具体算例，将模糊推理算法与左连续伪三角范数结合起来，为解决实际应用问题提供模糊推理算法的一种新的模型。尽管三I算法克服了CRI算法的一些缺陷,但是它没有充分考虑输入和规则前件的近似程度,使得在计算过程中会出现不合理的情形。因此,ZHOU等人在文献[9]中提出了模糊推理五蕴涵算法(五I算法),在推理的过程中充分考虑了A*和A(或B和B*)的接近程度,有效的改进了三I算法。文献[10]基于多型变元一阶形式系统MTL∀ms给出五I算法解的谓词形式表示,把五I算法纳入到严格的逻辑框架中。

1975年,ZADEH在文献[1]中提出了区间值模糊集。SAMBUC在文献[2]中也给出了区间值模糊集的概念,区间值模糊集元素的隶属度由单位区间[0,1]的闭子区间给出。由于区间值模糊集可以更好的描述不精确和不确定的信息,并且它能够有效地减少信息丢失。因此,许多研究者研究了这个问题,并且把模糊推理算法扩张到了区间值的情形。文献[12]把CRI算法扩张到了区间值的情形,并且讨论了区间值CRI算法的鲁棒性；文献[13]把三I算法扩张到了区间值的情形,并且讨论了区间值三I算法的鲁棒性,把模糊推理算法纳入到严格的逻辑框架中；文献[14]把反向三I算法扩张到了区间值的情形,并讨论了它的鲁棒性；文献[15]把五I算法扩张到了区间值的情形,并讨论了它的鲁棒性。文献[16]研究了多规则的区间值模糊推理。以上都是基于区间值可结合三角范数的推理算法,文献[17]给出了区间值t-可表示三角范数的定义，文献[18]给出的区间值可结合三角范数作为其特殊情形。虽然区间值三I算法克服了区间值CRI算法的缺陷，但是区间值三I算法在实际应用中会出现不合理的情形。因此,本文研究基于区间值t-可表示三角范数TT1,T2的模糊推理五蕴涵算法。

1 预备知识

令SI={[x,y]|x≤y,x,y∈[0,1]}。在SI上定义[a,b]≤[c,d],如果a≤c且b≤d,称该序关系为Kulisch-Miranke序[19]。[a,b]∧[c,d]=[a∧c,b∧d],[a,b]∨[c,d]=[a∨c,b∨d]。进一步,[a,b]∧[c,d]=[a,b]当且仅当[a,b]≤[c,d]当且仅当[a,b]∨[c,d]=[c,d]。容易证明代数结构(SI,∧,∨,[0,0],[1,1])是一个完备有界格。令X={x1,x2,…,xn}是一个非空集合,SI(X)为X的区间值模糊子集,A(xi)∈SI(A(xi)记为[Al(xi),Ar(xi)],1≤i≤n)。令A={[Al(x1),Ar(x1)],[Al(x2),Ar(x2)],…,[Al(xn),Ar(xn)]}和B={[Bl(x1),Br(x1)],[Bl(x2),Br(x2)],…,[Bl(xn),Br(xn)]}为两个区间值模糊集,A⊆B定义为Al(xi)≤Bl(xi),Ar(xi)≤Br(xi)(i=1,2,...,n)[20]。A的补集记为Ac(1≤i≤n),其中Ac={[1-Ar(x1),1-Al(x1)],[1-Ar(x2),1-Al(x2)],…,[1-Ar(xn),1-Al(xn)]}。对于任意非空子集A⊆SI,supA=[sup{x|[x,y]⊆A},sup{y|[x,y]⊆A}]。

定义1.1[21]设T:[0,1]2→[0,1]是二元算子,对于任意的a,b,c∈[0,1]满足下列条件:

1)T(a,b)=T(b,a)；(交换律)

2)T(T(a,b),c)=T(a,T(b,c))；(结合律)

3)T(a,c)≤T(b,c)其中a≤b；(单调性)

4)T(a,1)=a。(有界性)

称T为三角范数。

定义1.2[21]设T是三角范数,如果对于任意的(x0,y0)∈[0,1]2,任意的ε>0,存在δ>0,当(x,y)∈(x0-δ,x0]×(y0-δ,y0]时,有T(x,y)>T(x0,y0)-ε成立,称三角范数T是左连续的。

定义1.3[22]对于任意的x,x1,x2,y,y1,y2∈[0,1],映射R:[0,1]2→[0,1]称为模糊蕴涵,如果满足下列条件:

1)如果x1≤x2,则R(x1,y)≥R(x2,y),即R(·,y)是单调递减的；

2)如果y1≤y2,则R(x,y1)≤R(x,y2),R(x,·)即是单调递增的；

3)R(0,0)=1；

4)R(1,1)=1；

5)R(1,0)=0。

定义1.4[23]对于任意的a,b∈[0,1],由左连续三角范数T诱导的剩余蕴涵为

R(a,b)=sup{x∈[0,1]|T(a,x)≤b},∀a,b∈[0,1]。

例1.1[24]四个重要的三角范数及其剩余蕴涵:

1)Gödel三角范数TG及其剩余蕴涵RG:

TG(a,b)=a∧b,

2)极小三角范数T0及其剩余蕴R0:

3)Goguen三角范数TG0及其剩余蕴涵RG0:

TG0(a,b)=ab,

4)Lukasiewicz三角范数TL及其剩余蕴涵RL:

TL(a,b)=0∨(a+b-1),

RL(a,b)=1∧(1-a+b)。

定义1.5[25]设TT1,T2是SI×SI→SI上的映射,T1,T2是[0,1]上的三角范数,T1≤T2,对于任意的[a,b],[c,d],∈SI满足下列条件:

1)TT1,T2([a,b],[c,d])=TT1,T2([c,d],[a,b])；(交换律)

2)TT1,T2(TT1,T2([a,b],[c,d]),[e,f])=TT1,T2([a,b],TT1,T2([c,d],[e,f]))；(结合律)

3)TT1,T2([a,b],[e,f])≤TT1,T2([c,d],[e,f]),其中[a,b]≤[c,d]；(单调性)

4)TT1,T2([1,1],[a,b])=[a,b]。(有界性)称TT1,T2为SI上的三角范数。

定义1.6[18]设TT1,T2是SI×SI→SI上的映射,T1,T2是[0,1]上的三角范数,T1≤T2,对于任意的[a,b],[c,d]∈SI,定义:

TT1,T2([a,b],[c,d])=[T1(a,c),T2(b,d)]。

称TT1,T2为区间值t-可表示三角范数。

注1.1如果T1=T2=T,则

TT1,T2([a,b],[c,d])=T([a,b],[c,d])=[T(a,c),T(b,d)]是区间值可结合三角范数[1]。

定义1.7如果T1和T2是左连续三角范数,称区间值t-可表示三角范数TT1,T2是左连续区间值三角范数。

定义1.8[26]映射→:SI×SI→SI称为区间值模糊蕴涵,如果满足下面两个条件:

1)关于第一个变量单调递减,关于第二个变量单调递增；

2)[0,0]→[0,0]=[1,1],[0,0]→[1,1]=[1,1],[1,1]→[1,1]=[1,1],[1,1]→[0,0]=[0,0]。

定义1.9[18]设TT1,T2是区间值t-可表示三角范数,称

RT1,T2([a,b],[c,d])=∨{[x,y]∈SI|

TT1,T2([a,b],[x,y]≤[c,d]}

为由左连续区间值t-可表示三角范数TT1,T2诱导的剩余蕴涵。

引理1.2[27]区间值三角范数TT1,T2满足剩余原则当且仅当TT1,T2满足TT1,T2([x1,y1],supA)=sup{TT1,T2([x1,y1],[x,y])|[x,y]∈A⊆SI}。

引理1.3[27]设R1和R2是由左连续三角范数T1和T2诱导的剩余蕴涵,且有T1≤T2,则由左连续区间值t-可表示三角范数TT1,T2诱导的剩余蕴涵RT1,T2有如下形式:

RT1,T2([a,b],[c,d])=[R1(a,c)∧R2(b,d),R2(b,d)]。

定理1.1区间值t-可表示三角范数TT1,T2左连续的充要条件是TT1,T2满足剩余原则,即TT1,T2([x,y],[x1,y1])≤[x2,y2]⟺[x,y]≤RT1,T2([x1,y1],[x2,y2]),并且区间值剩余蕴涵RT1,T2有如下形式:RT1.T2([a,b],[c,d])=[R1(a,c)∧R2(b,d),R2(b,d)],其中R1和R2是由左连续三角范数T1和T2(T1≤T2)诱导的剩余蕴涵。

证明(⟸)因为TT1,T2满足剩余原则,由引理1.2得,TT1,T2([x1,y1],sup[x,y])=supTT1,T2([x1,y1],[x,y]),TT1,T2([x1,y1],[supx,supy])=supTT1,T2([x1,y1],[x,y]),[T1(x1,supx),T2(y1,supy)]=sup[T1(x1,x),T2(y1,y)]=[supT1(x1,x),supT2(y1,y)],因此T1(x1,supx)=supT1(x1,x),T2(y1,supy)=supT2(y1,y)。

根据引理1.1,因为T1和T2是[0,1]上的左连续三角范数且有T1≤T2,所以区间值t-可表示三角范数TT1,T2是左连续的。

(⟹)设区间值t-可表示三角范数TT1,T2是左连续的,则

TT1,T2([x,y],[x1,y1])=[T1(x,x1),T2(y,y1)]≤[x2,y2]

⟺T1(x,x1)≤x2&T2(y,y1)≤y2&x≤y,x1≤y1,x2≤y2

⟺x≤R1(x1,x2)&y≤R2(y1,y2)&x≤y≤R2(y1,y2),x1≤y1,x2≤y2

⟺x≤R1(x1,x2)∧R2(y1,y2)&y≤R2(y1,y2)&x1≤y1,x2≤y2

⟺[x,y]≤[R1(x1,x2)∧R2(y1,y2),R2(y1,y2)]=RT1,T2([x1,y1],[x2,y2])。

定义1.10[28]对于任意[X,Y]=([x1,y1],[x2,y2],…,[xn,yn]),[X′,Y′]=([x1′,y1′],[x2′,y2′],…,[xn′,yn′])∈SIn,d([X,Y],[X′,Y′])=max{maxi{|xi-xi′|,|yi-yi′|}}叫做Moore距离。

2 基于区间值t-可表示三角范数的模糊推理五蕴涵算法

设TT1,T2是区间值t-可表示三角范数,RT1,T2是由左连续区间值t-可表示三角范数TT1,T2诱导的剩余蕴涵。在本文中,把TT1,T2简记为T,把RT1,T2简记为R。

基于区间值t-可表示三角范数的五I算法的模型(FMP):

R(R(A(x),B(y)),R(R(A*(x),A(x)),R(A*(x),B*(y))))=[1,1]。

(1)

基于区间值t-可表示三角范数的五I算法的模型(FMT):

R(R(A(x),B(y)),R(R(B(y),B*(y)),R(A(x),A*(x))))=[1,1]。

(2)

定义2.1基于区间值t-可表示三角范数的五I算法(FMP):设A(x),A*(x)∈SI(X),B(y)∈SI(Y)。令M(x,y)=R(R(A(x),B(y)),R(R(A*(x),A(x)),R(A*(x),[1,1]))),B(A,B,A*)={C(y)∈SI(Y)|R(R(A(x),B(y)),R(R(A*(x),A(x)),R(A*(x),C(y))))=M(x,y),x∈X,y∈Y}。当集合B(A,B,A*)的最小元存在(记做B*(y))时,称B*(y)为FMP问题的基于区间值t-可表示三角范数的五I算法的解。

定义2.2基于区间值t-可表示三角范数的五I算法(FMT):设A(x)∈SI(X),B(y),B*(y)∈SI(Y)。令N(x,y)=R(R(A(x),B(y)),R(R(B(y),B*(y)),R(A(x),[1,1]))),A(A,B,B*)={D(x)∈SI(X)|R(R(A(x),B(y)),R(R(B(y),B*(y)),R(A(x),D(x))))=N(x,y),x∈X,y∈Y}。当集合A(A,B,B*)的最小元存在(记做A*(x))时,称A*(x)为FMT问题的基于区间值t-可表示三角范数的五I算法的解。

定理2.1设R是由左连续区间值t-可表示三角范数T诱导的剩余蕴涵,则FMP问题的基于区间值t-可表示三角范数的五I算法的解B*(y)为

(3)

证明首先,证明B*(y)是使得等式(1)成立的Y上的区间值模糊集。由(3)式得:T(R(A(x),B(y)),R(A*(x),A(x)),A*(x))≤B*(y)。由于R是左连续区间值t-可表示三角范数T诱导的剩余蕴涵,由剩余原则可得:T(R(A(x),B(y)),R(A*(x),A(x)))≤R(A*(x),B*(y)),R(A(x),B(y))≤R(R(A*(x),A(x)),R(A*(x),B*(y)))。因此,R(R(A(x),B(y)),R(R(A*(x),A(x)),R(A*(x),B*(y))))=[1,1]。

R(R(A(x),B(y)),R(R(A*(x),A(x)),R(A*(x),C(y))))=[1,1]

当且仅当R(A(x),B(y))≤R(R(A*(x),A(x)),R(A*(x),C(y)))

当且仅当T(R(A(x),B(y)),R(A*(x),A(x)))≤R(A*(x),C(y))

当且仅当T(R(A(x),B(y)),R(A*(x),A(x))A*(x))≤C(y)。

于是对于所有的x,y,B*(y)≤C(y),因此B*(y)是使得等式(1)成立的Y上的最小区间值模糊集,即B*(y)是FMP问题的基于区间值t-可表示三角范数的五I算法的解。

定理2.2设R是左连续区间值t-可表示三角范数T诱导的剩余蕴涵,则FMT问题的基于区间值t-可表示三角范数的五I算法的解A*(x)为

(4)

证明首先,证明A*(x)是使得等式(2)成立的X上的区间值模糊集。由(4)式得:

T(R(A(x),B(y)),R(B(y),B*(y)),A(x))≤A*(x)。因为R是由左连续区间值t-可表示三角范数T诱导的剩余蕴涵,由剩余原则可得:

T(R(A(x),B(y)),R(B(y),B*(y)))≤R(A(x),A*(x)),R(A(x),B(y))≤R(R(B(y),B*(y)),’(A(x),A*(x)))。因此,’(A(x),B(y)),’(B(y),B*(y)),’(A(x),A*(x))))=[1,1]。

其次,证明A*(x)是使得等式(2)成立的X上的最小区间值模糊集。设D(x)是X上使得等式(2)成立的区间值模糊集。由剩余原则得:

R(R(A(x),B(y)),R(R(B(y),B*(y)),R(A(x),D(x))))=[1,1]

当且仅当R(A(x),B(y))≤R(R(B(y)B*(y)),R(A(x),D(x)))

当且仅当T(R(A(x),B(y)),R(B(y),B*(y)))≤R(A(x),D(x))

当且仅当T(R(A(x),B(y)),R(B(y),B*(y)),A(x))≤D(x)。

于是对于所有的x,y,A*(x)≤D(x),因此A*(x)是使得等式(2)成立的X上的最小区间值模糊集,即A*(x)是FMT问题的基于区间值t-可表示三角范数的五I算法的解。

命题2.11)如果存在x0∈X使得A(x0)=[1,1],则FMP问题的基于左连续区间值t-可表示三角范数T的五I算法是还原的。

2)如果存在y0∈Y使得B(y0)=[1,1],则FMT问题的基于左连续区间值t-可表示三角范数T的五I算法是还原的。

证明1)假设A*(x)=A(x)并且存在x0∈X使得A(x0)=[1,1],则

≥T(R(A(x0),B(y)),R(A*(x0),A(x0)),A*(x0))

=T(R([1,1],B(y)),R([1,1],[1,1]),[1,1])

=B(y)。

即B(y)≥B*(y)≥B(y),因此B*(y)=B(y),因此FMP问题的基于左连续区间值t-可表示三角范数T的五I算法是还原的。

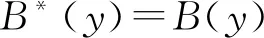
A(x)≥A*(x)

≥T(R(A(x),B(y0)),R(B(y0),B*(y0)),A(x))

=T(R(A(x),[1,1]),R([1,1],[1,1]),A(x))

=A(x)。

即A(x)≥A*(x)≥A(x),因此A*(x)=A(x),因此FMT问题的基于左连续区间值t-可表示三角范数T的五I算法是还原的。

3 基于区间值t-可表示三角范数的模糊推理五蕴涵算法的鲁棒性

定义3.1[12]设f是从SIn到SI的n-元映射,ε∈[0,1]。对于任意的[x,y]=([x1,y1],

[x2,y2],…,[xn,yn]∈SIn,函数f在点[x,y]处的ε-灵敏度为：

Δf([x,y],ε)=∨{d(f([x,y]),f([x′,y′]))|[x′,y′]∈SIn,dn([x,y],[x′,y′])≤ε},其中,

定义3.2[12]函数f的ε最大灵敏度为

定义3.3[12]设f和f′是两个n-元区间值模糊连接词。如果对任意的ε>0,Δf(ε)≤Δf′(ε),则称f至少比f′鲁棒。进一步,如果存在ε>0使得Δf(ε)≤Δf′(ε),则f比f′鲁棒。

引理3.1[12]区间值Gödel三角范数TG是最鲁棒的区间值三角范数,且ΔTG(ε)=ε。

引理3.2[12]区间值Lukasiewicz蕴涵RL是区间值上最鲁棒的剩余蕴涵,且ΔRL(ε)=2ε∧1。

ΔB*(ε)=‖B*-B′*‖∞≤ΔT(ΔT(ΔR(ε)))。

证明

ΔB*(ε)=‖B*-B′*‖∞

≤ΔT(ΔT(ΔR(ε))∨ε)。

由引理3.1、引理3.2得:ΔR(ε)≥2ε∧1>ε,所以ΔT(ΔR(ε))≥ΔR(ε)>ε,即

ΔT(ΔR(ε))∨ε=ΔT(ΔR(ε))。因此

ΔB*(ε)=‖B*-B′*‖∞≤ΔT(ΔT(ΔR(ε)))。

ΔA*(ε)=‖A*-A′*‖∞≤ΔT(ΔT(ΔR(ε)))。

证明

ΔA*(ε)=‖A*-A′*‖∞

R(B′(y),B′*(y)),A′(x)))

≤ΔT(ΔT(ΔR(ε))∨ε)。

由引理3.1、引理3.2得:ΔR(ε)≥2ε∧1>ε,所以ΔT(ΔR(ε))≥ΔR(ε)>ε,即

ΔT(ΔR(ε))∨ε=ΔT(ΔR(ε))。因此ΔA*(ε)=‖A*-A′*‖∞≤ΔT(ΔT(ΔR(ε)))。

4 模式识别中的应用

因为区间值模糊集和直觉模糊集是等价的,因此,给出基于直觉模糊集的以下定义,类似的,给出基于区间值模糊集的相关定义。

定义4.1[29]设αi=[μαi,ναi](i=1,2,…,n)是一个直觉模糊集.如果

注4.1设Ai=[Ail,Air](i=1,2,…,n)是一个区间值模糊集。如果

定义4.2[30]设α=[μα,να]和β=[μβ,νβ]是两个直觉模糊集,α和β的分数函数分别定义为s(α)=μα-να和s(β)=μβ-νβ；α和β的精确函数分别定义为h(α)=μα+να和h(β)=μβ+νβ。

1)如果s(α)

2)如果s(α)=s(β),则

a)如果h(α)=h(β),则α等于β,记为α=β；

b)如果h(α)

注4.2设A=[a,b]和B=[c,d]是两个区间值模糊集,A和B的分数函数分别定义为s(A)=a+b-1和s(B)=c+d-1；A和B的精确函数分别定义为h(A)=a-b+1和h(B)=c-d+1。

1)如果s(A)

2)如果s(A)=s(B),则

a)如果h(A)=h(B),则A等于B,记为A=B；

b)如果h(A)

4.1 模式识别算法

设Y={y1,y2,…,yn}是一个模式集,X={x1,x2,…,xm}是一个属性集,Ai(xj)是属性xj对于模式yi(i=1,2,…,n,j=1,2,…,m)的值,A*(xj)是属性xj对于样本S的值,B(yi)是模式的值,表1是模式属性统计数据,表2是样本属性统计数据。方法如下：

表1 模式属性统计数据Table 1 Statistic data of the attribute and the pattern

表2 样本属性统计数据Table 2 Statistic data of the attribute and the sample

第一步:用区间值模糊加权平均算子IVFWA(注4.1)分别聚合Ai(xj)和A*(xj)

(j=1,2,…,m),记为Ai和A*；

第二步:计算区间值剩余蕴涵R(Ai,B(yi))(i=1,2,…,n)；

第三步:计算区间值剩余蕴涵R(A*,Ai)(i=1,2,…,n)；

第四步:计算左连续区间值t-可表示三角范数T(R(Ai,B(yi)),R(A*,Ai),A*),则我们能得到B*(yi)(i=1,2,…,n)的值；

第五步:对B*(yi)的值进行排序(注4.2),选择最大值B*(yi0),则这个样本属于模式yi0。

4.2 医疗诊断中的应用

例4.1设Y={y1,y2,y3,y4,y5}是五种疾病,其中yi(i=1,2,3,4,5)分别代表“病毒性发热”,“疟疾”,“伤寒”,“胸部问题”和“胃病”。设X={x1,x2,x3,x4,x5}是五种临床症状,其中xj(j=1,2,3,4,5)代表“体温”,“头疼”,“咳嗽”,“胸痛”和“胃疼”。设B(yi)是疾病的值。表3给出了疾病症状和病人症状统计数据。令

表3 疾病症状和病人症状统计数据Table 3 Statistic data of the diagnoses

注：①为病毒性发热,②为疟疾,③为伤寒,④为胸部问题,⑤为胃病。

B(y1)=[0.20,0.40],

B(y2)=[0.30,0.60],

B(y3)=[0.35,0.66],

B(y4)=[0.30,0.60]，

B(y5)=[0.70,0.80]。

我们使用上面的方法来判断病人Q患哪种疾病。

设R1是左连续Lukasiewicz三角范数T1诱导的剩余蕴涵,R2是左连续Gödel三角范数T2诱导的剩余蕴涵。设

T([a,b],[c,d])=[T1(a,c),T2(b,d)],其中T1(a,c)=TL(a,c),T2(b,d)=TG(b,d),则:

第一步:令ωi=1/5,(i=1,2,3,4,5)。用区间值模糊加权平均算子IVFWA(注4.1)分别聚合Ai(xj)和A*(xj)(j=1,2,3,4,5),记为Ai和A*,则:

A1=[0.59,0.69],A2=[0.61,0.76],

A3=[0.65,0.78],A4=[0.60,0.74],

A5=[0.64,0.78],A*=[0.72,0.82]；

第二步:计算区间值剩余蕴涵R(Ai,

B(yi))(i=1,2,…,n):

R(A1,B(y1))=[0.91,1.00],R(A2,B(y2))=[0.70,0.70],

R(A3,B(y3))=[0.75,0.75],

R(A4,B(y4))=[0.95,1.00],

R(A5,B(y5))=[1.00,1.00];

第三步:计算区间值剩余蕴R(A*,Ai)

(i=1,2,3,4,5):

R(A*,A1)=[0.69,0.69],

R(A*,A2)=[0.76,0.76],

R(A*,A3)=[0.78,0.78],

R(A*,A4)=[0.74,0.74],

R(A*,A5)=[0.78,0.78]；

第四步:计算左连续区间值t-可表示三角范数T(R(Ai,B(yi)),R(A*,Ai),A*),则我们能得到B*(yi)(i=1,2,3,4,5)的值:

B*(y1)=[0.32,0.69],

B*(y2)=[0.18,0.70],

B*(y3)=[0.25,0.75],

B*(y4)=[0.41,0.74],

B*(y5)=[0.50,0.78]；

第五步:对B*(yi)的值进行排序(注4.2):B*(y5)>B*(y4)>B*(y1)>B*(y3)>B*(y2),

B*(y5)为最大值,所以病人Q患的病为胃病(y5)。

4.3 模式识别中的应用

例4.2设Y={y1,y2,y3}是模式集,X={x1,x2,x3}是属性集,Ai(xj)是属性xj对于模式yi(i=1,2,3,j=1,2,3)的值,A*(xj)是属性xj对于样本S的值。设B(yi)是模式的值。

B(y1)=[0.20,0.30],

B(y2)=[0.50,0.70],

B(y3)=[0.50,0.80]。

表4给出了模式属性和样本属性统计数据。我们使用以上方法判断样本S属于哪个模式。

表4 模式属性和样本属性统计数据Table 4 Statistic data of the pattern and the sample

设R1是左连续Lukasiewicz三角范数T1诱导的剩余蕴涵,R2是左连续Gödel三角范数T2诱导的剩余蕴涵。设

T([a,b],[c,d])=[T1(a,c),T2(b,d)],其中T1(a,c)=TL(a,c),T2(b,d)=TG(b,d),则:

第一步:令ωi=1/3,(i=1,2,3)。用区间值模糊加权平均算子IVFWA(注4.1)分别聚合Ai(xj)和A*(xj)(j=1,2,3),记为Ai和A*,则:

A1=[0.30,0.40],A2=[0.50,0.70],

A3=[0.57,0.73],A*=[0.50,0.70]；

第二步:计算区间值剩余蕴涵R(Ai,B(yi))(i=1,2,3)：

R(A1,B(y1))=[0.30,0.30],

R(A2,B(y2))=[1.00,1.00],

R(A3,B(y3))=[0.93,1.00]；

第三步:计算区间值剩余蕴涵R(A*,Ai)(i=1,2,3):

R(A*,A1)=[0.40,0.40],

R(A*,A2)=[1.00,1.00],

R(A*,A3)=[1.00,1.00]；

第四步:计算左连续区间值t-可表示三角范数T(R(Ai,B(yi)),R(A*,Ai),A*),则我们能得到B*(yi)(i=1,2,3)的值:

B*(y1)=[0.00,0.30],B*(y2)=[0.50,0.70],

B*(y3)=[0.43,0.70]；

第五步:对B*(yi)的值进行排序(注4.2):B*(y2)>B*(y3)>B*(y1),B*(y2)为最大值,所以样本S属于模式y2。

5 结 语

本文给出基于区间值t-可表示三角范数TT1,T2的模糊推理五蕴涵算法,文献[15]中的区间值模糊推理五蕴涵算法是其特殊情形。讨论了算法的还原性和鲁棒性,并将其应用于模式识别问题。