空沟隔振对瑞利波传播影响的理论研究
姚锦宝,胡敬梁
(北京交通大学 土木建筑工程学院, 北京 100044)
轨道交通对环境的影响主要表现为噪声和沿地基传播的振动,其已被列为七大环境公害之一[1]。地铁列车运行持续时间长且频繁,运行期间引起的地面及建筑物的振动所持续时间可达到地铁每天总运营时间的15%~20%[2];试验研究表明:振动强度越高,对人们的影响也就越大[3]。
对列车引起环境振动的隔振研究中,常以采取屏障隔振措施后的地表振动问题研究为主。比较常见的传播路径上隔振措施有空沟、填充沟及隔振屏障。Woods[4]通过试验手段,研究了空沟的隔振效果;Tulika等[5]采用3D有限元模型,分析了空沟和填充沟关键参数的隔振效率,得到沟槽几何和材料特性的最佳值;Adam等[6]采用数值方法,分析了空沟及填充沟的隔振特性;高广运等[7]理论分析了多排桩隔振屏障对Rayleigh波的多层驱散问题;冯牧等[8]将实测和数值模拟相结合, 分析了隔振沟对地铁周边建筑物的隔振效果;Coulier[9]采用实测和数值分析相结合的方法,研究了土体中的刚性介质对波的传播影响;Yang等[10]运用2.5维方法,分析了开放式和填充式沟槽对铁路沿线建筑物的隔振效果。此外,冯桂帅等[11]采用实测与模型试验方法,比较了典型的隔振屏障,如填充沟、空沟及排桩等的隔振效果。
运行列车引发的土体振动中,相对于瑞利波而言,体波衰减较快,未衰减的瑞利波占比仍然很大。研究表明,环境振动中,瑞利波占比达67%[10],因此,研究屏障隔振对瑞利波的衰减规律较有实际意义。对于空沟的隔振效果,过去多采用数值分析和现场试验的研究方法,鲜有采用理论解析的方法。本文采用理论解析方法,研究了空沟对瑞利波的隔振效果。
1 空沟对土体振动隔振理论研究
振动在弹性介质中的传播过程称为弹性波。振动会在弹性体界面产生表面波,瑞利波是最常见的表面波。列车引起土体的振动,常以瑞利波形式在地表面上向远处传播。
1.1 瑞利波的传播与衰减
瑞利波主要位于土体自由表面下0.15λ~0.2λ(λ为波长)深度处,在水平及竖向两个方向产生运动,并有明显的振动轨迹分界线,分界线上部质点的运动呈后退椭圆形,竖向运动一般滞后于水平运动,如图1所示。
在均匀各向同性的自由半空间中,可以计算瑞利波的竖向和水平向位移振幅归一化值。
作用于原点的集中简谐荷载为f(t)=Peiωt(P为幅值),当拾振点与振源相距较大时,瑞利波对波场竖向位移和水平位移贡献[12]可表示为
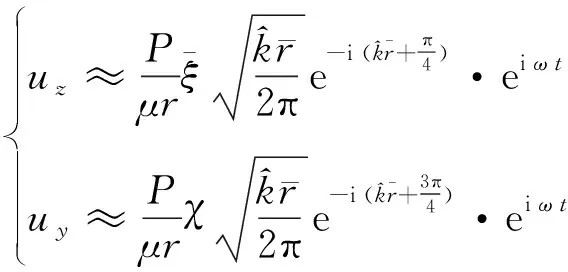
(1)
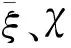
1.2 弹性波在变截面区域的反射与透射
简谐集中荷载作用在土体自由表面时,其表现形式为柱面波;传播距离较大时,波阵面接近于水平面。
在频域内,土体的振动响应虽为3维,但由于在垂直于轨道方向上,任意两截面的动力响应,会因为位置不同存在一个相位差。由此,可将3维响应问题减少为2.5维问题,对任一截面的动力响应,进行离散求解。
远场的空沟隔振示意见图2,其截面为矩形,主要参数有沟深、沟宽、振源与沟内侧边缘距离。
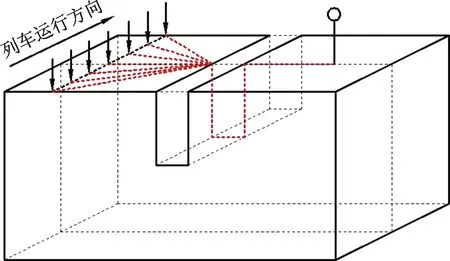
图2 空沟隔振示意
波动在两种介质分界面上的反射和透射见图3。两个均匀、各向同性弹性半空间在分界面上相互连结。假定平面波自下向上入射,设入射波为剪切波,根据分界面连续条件,可以确定反射波与透射波。
图3 介质分界面的反射与透射
位移的入射、反射和透射系数分别为
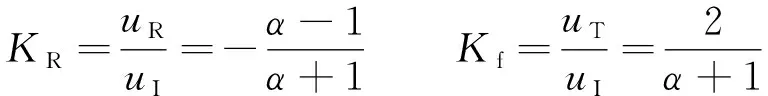
(2)
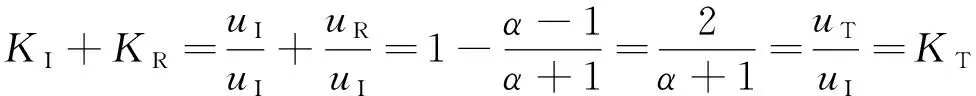
(3)
式中:KI、KR、KT分别为入射系数、反射系数、透射系数;α为上部介质波阻抗与下部介质波阻抗的比值;uI、uR、uT分别为入射波、反射波、透射波位移。
式(2)、式(3)中,界面两侧的面积相同;当空沟存在时,空沟底部犄角处界面两侧的截面不同,阻抗计算需考虑面积的影响。
瑞利波沿自由表面传播,振动随深度快速衰减,在无穷深处,位移趋于零,即大部分振动能量分布在地表以下大约1.5λR深度范围内(λR为瑞利波波长),1.5λR深度以外的振动响应很小,本文忽略不计。空沟底部犄角处的设置见图4,图4中:h、w分别为沟深、沟宽,沟长取单位长度;I1、I2分别为不同界面的入射波。
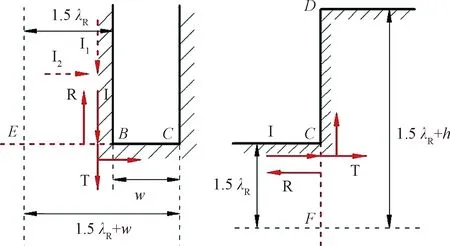
图4 沟底犄角处反射与透射
考虑截面面积,阻抗α=ρ2c2A2/ρ1c1A1,ρcA在不同文献中有不同的解释。杨桂通等[13]研究了杆性质突变处的反射和透射;黎在良等[14]对两种介质内界面的反射和透射做了阐述;王从约等[15]在研究应力波在非均质变截面杆中传播问题中,定义ρcA为声阻抗。
1.3 空沟传播路径的公式推导
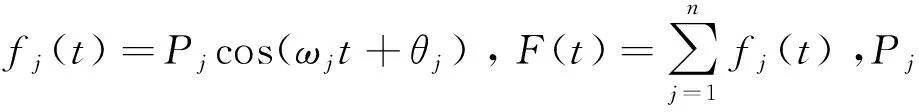
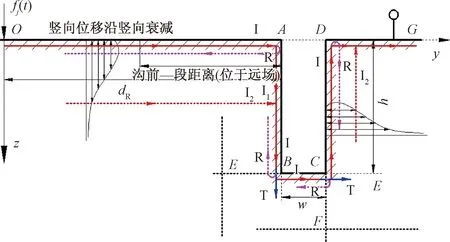
图5 瑞利波沿地基及空沟传播二维示意图
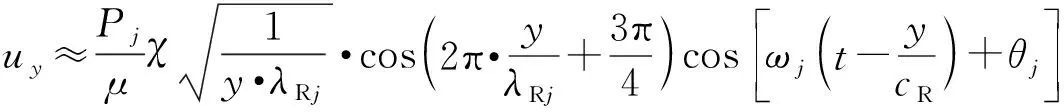
(4)
式中:cR、λRj分别为瑞利波的波速与波长。
在二维平面内,瑞利波沿空沟和空沟外侧土体自由表面位移的推演过程如下:
(1)OA段
OA段的位移包括两部分,一部分为来自振源的入射波,另一部分为入射波经左侧空沟壁反射产生的反射波。对于地表上空沟内侧任意点,反射波相对于入射波,需要考虑时间和传播距离引起的相位差。反射波引起的位移为

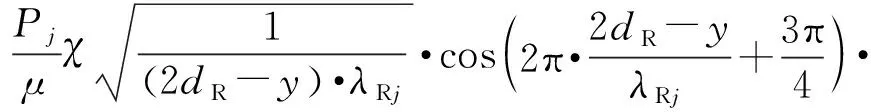
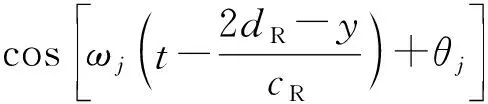
(5)
当时间t≥(2dR-y)/cR时,OA段地表总位移等于入射波与反射波叠加响应,转角A点的位移为
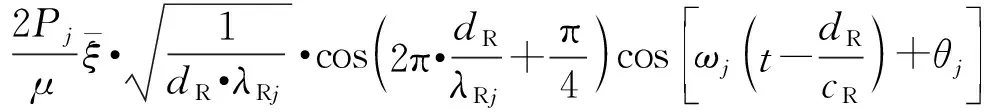
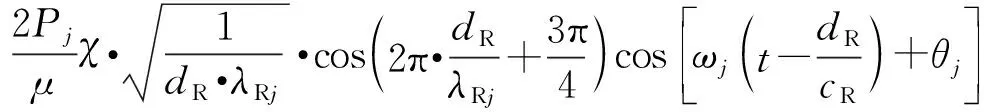
(6)
当空沟的埋置深度足够大,入射波遇空沟内侧壁反射,振动的绝大部分沿原路返回,OA段入射波与反射波叠加时,产生的响应接近于入射波在无空沟时相同位置相应的2倍。
(2)AB段
振动通过边缘A沿AB段往下传播相对于交界面BE的入射波包括两部分:瑞利波沿AB段传播引起的位移和在z=h水平方向上向右传播在AB上引起的位移;两者考虑因时间和距离产生相位的条件下进行叠加计算,即得到相对于交界面BE的入射波,即
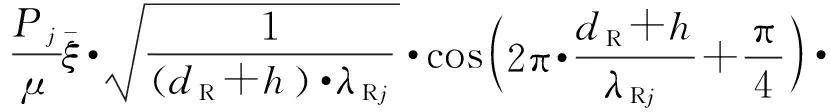
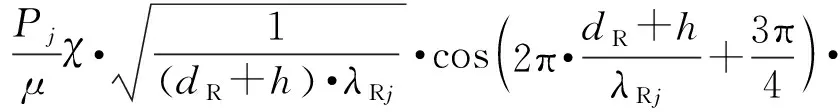
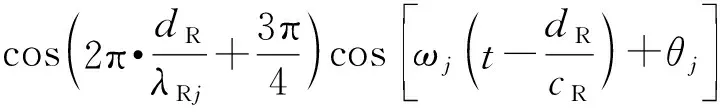
(7)
(3)BC段
在分界面BE处,根据式(3)得到的连续条件,瑞利波过点B后,沿空沟底部自由表面传播,对于分界面CF而言是入射波,根据分界面的反射与透射得出

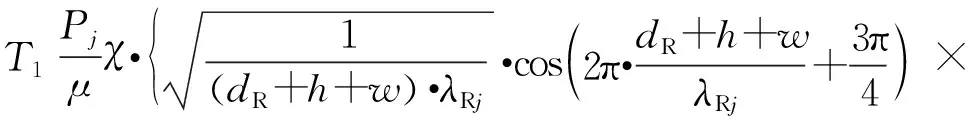
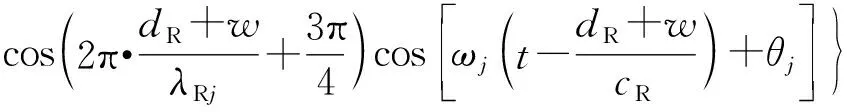
(8)
(4)CD段
根据分界面CF处的连续条件,采用与界面BE相同的处理方法,得出CD段上相对于界面CF的入射波,即
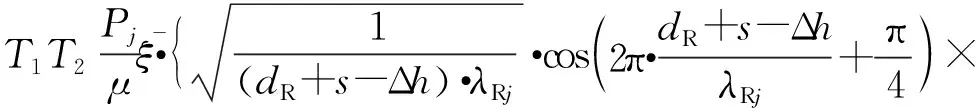
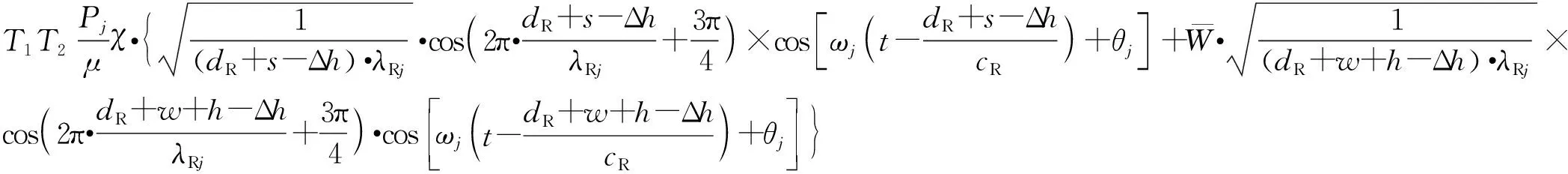
(9)
(5)DG段
沿空沟外侧沟壁竖向段CD传播的瑞利波,位移随深度的增大而衰减;同时,沿垂直于空沟外侧沟壁CD以下某一深度的水平和竖向位移在该水平位置沿z轴负方向传播,与土体自由面上DG段相遇后产生反射波的同时,沿DG段传播,引起空沟外侧土体自由表面的振动。
粘液腺囊肿被视为口腔科疾病之一,它是一种口腔粘液腺导管因受到外伤后发生破裂,涎粘蛋白分泌物潴留于腺体组织内,所引起的腺泡逐渐膨胀而形成的囊肿。囊肿多发生于下唇,其次是舌尖、舌腹部以及颊粘膜等处。症状为局部肿胀,患处有淡紫蓝色半透明且质地柔软的囊性肿块,易破溃,破溃排出液体数日后会反复发作,病程可数天到数月。本文在梳理腺上皮和粘液腺的组织细胞学知识的基础上,综合分析了粘液腺囊肿这种疾病的治疗方法以及各种方法的优点和不足。
波在过D点沿DG传播过程中,CD上质点的竖向振动转变为DG的水平振动,CD上质点的水平振动转化为DG段的竖向振动。O点简谐荷载在DG段引起的竖向位移和水平位移为


(10)
瑞利波随深度的增加快速衰减;当沟深大于1.5λR波长时,式(10)中的第二项与第一项相比可忽略。
1.4 多点激励下位移计算
如图6所示,地表上任一拾振点P的振动响应,可认为是由多个集中简谐荷载的叠加,需要同时考虑时间和位置两个因素引起的相位变化,图中d为荷载列的距离[17]。
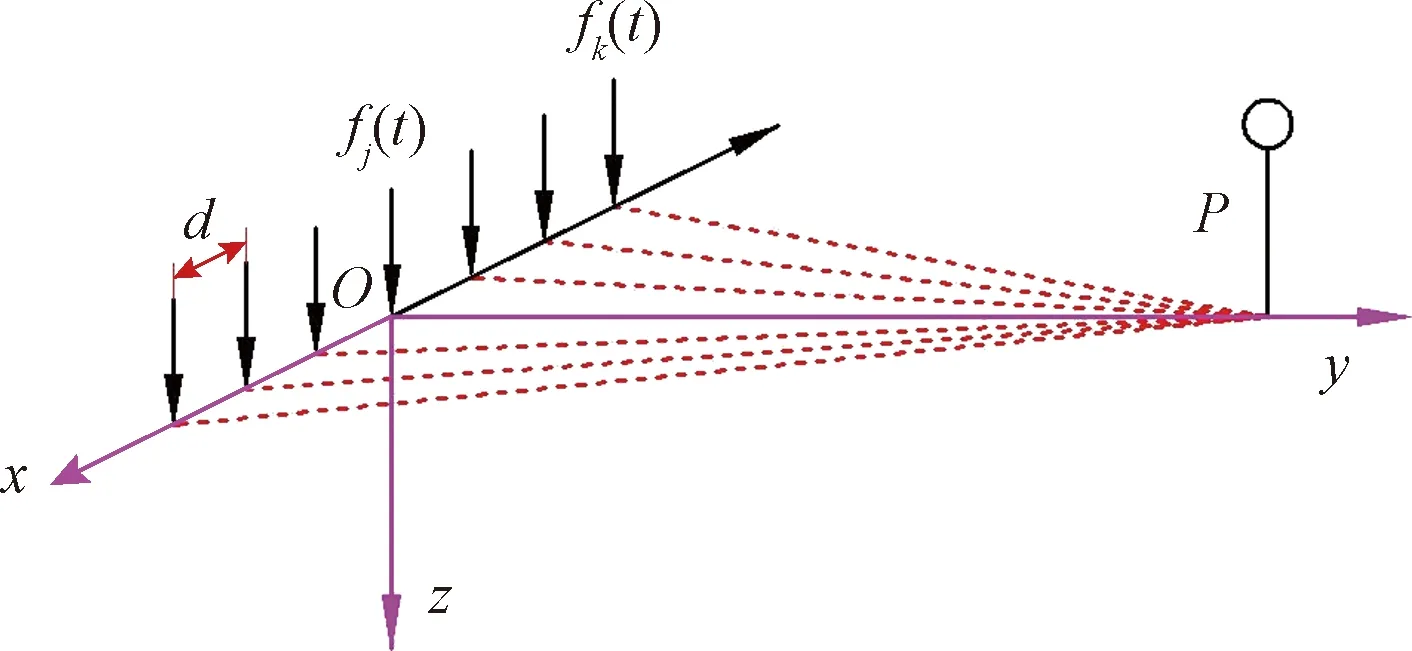
图6 多个竖向简谐荷载叠加示意
若激振点处的作用力时程曲线f(t)呈非周期性变化,可以对其进行快速傅里叶变换(FFT),得到的一系列周期性集中简谐荷载的叠加。
振源列中除O点以外其他位置的激振点fk(t)在DG段引起的竖向位移uz和水平位移uy为
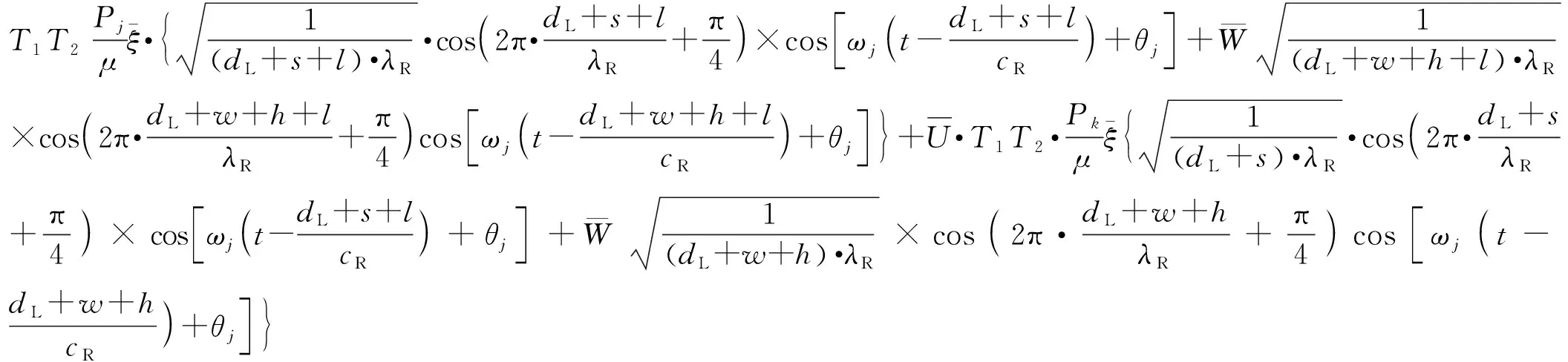
(11)
2 有无空沟时远场土体地表响应的对比
根据以上理论推导,讨论在有无空沟的工况下,土体表面上任一点(空沟外侧,无沟时为相应的对应点)的振动响应对比。
地基表面瑞利波速为75 m/s,空沟内侧边缘与O点处激振点的距离dR=25 m,空沟埋深h=4 m,沟宽w=1 m,拾振点距离空沟外侧边缘的距离分别为l=2、4、6、8、10 m(分别对应无空沟地基上与振源的距离d=28、30、32、34、36 m)。施加的竖向荷载为周期性简谐荷载,P=8 kN,频率ω变化设定为1、5、10、…、35、40 Hz,此次计算不考虑相位变化。空沟的加载模型见图7。
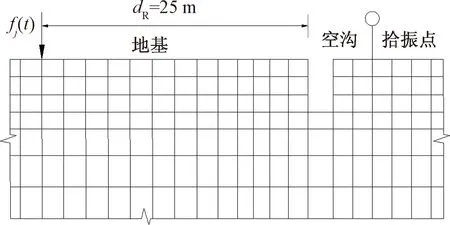
图7 含空沟的土体表面加载示意
作用在振源处土体上竖向荷载的时程曲线如图8所示。
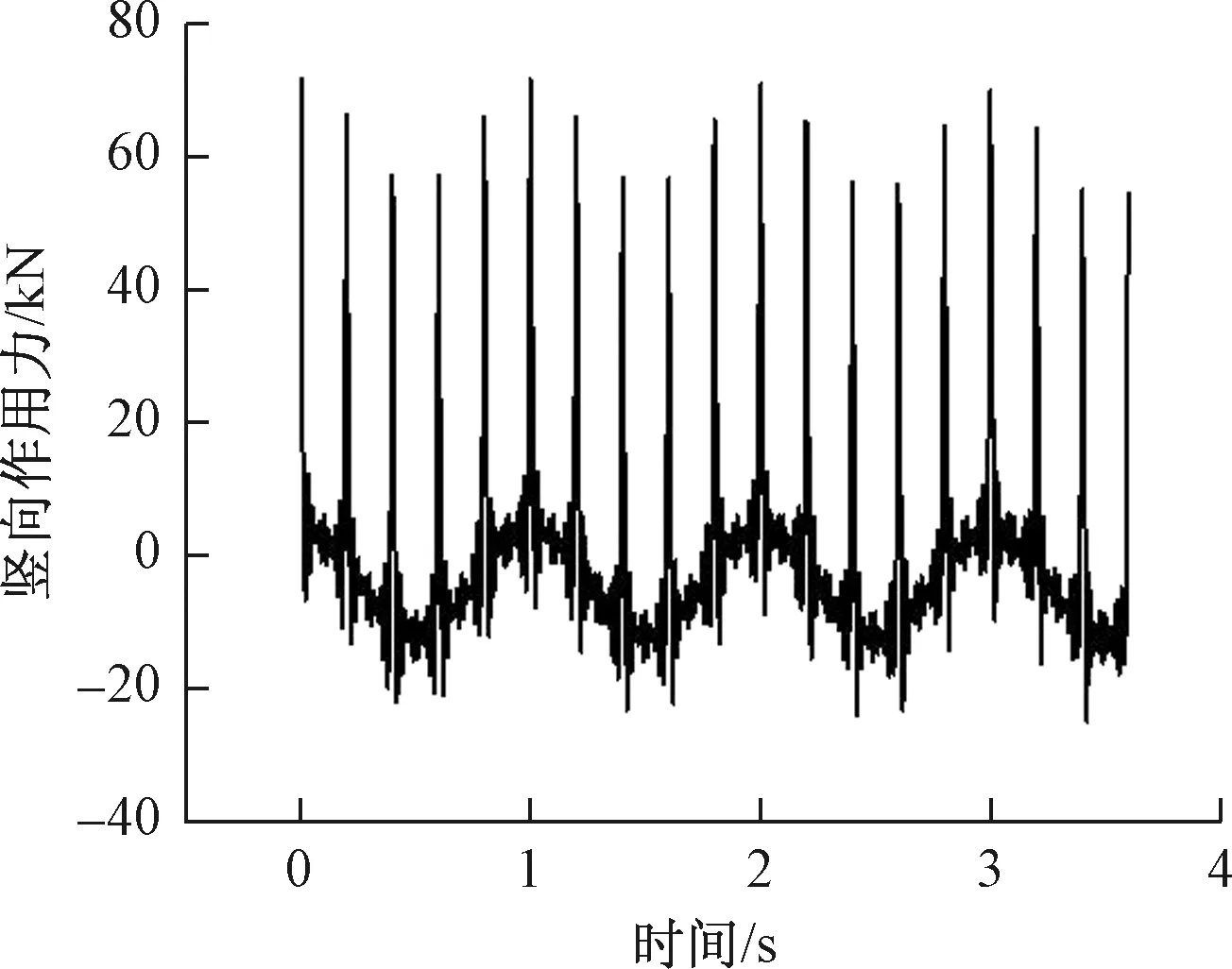
图8 振源处的竖向荷载时程曲线
图10为距离空沟外侧边缘l分别为2、4、6、8、10 m处土体的竖向和水平向振动加速度的频谱分析图;土体表面各点的竖向加速度振级见表1。
从图9、图10和表1中可以看出:
(1) 同一位置处,土体竖向加速度的幅值大于相对应水平向加速度的幅值;有沟状况下土体振动幅值大于无沟下的振动幅值。
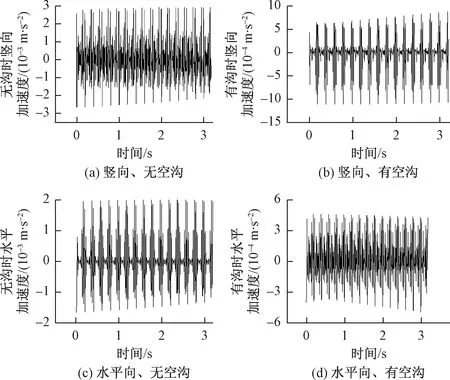
图9 有无空沟时土体加速度时程对比分析 (dR=28 m)
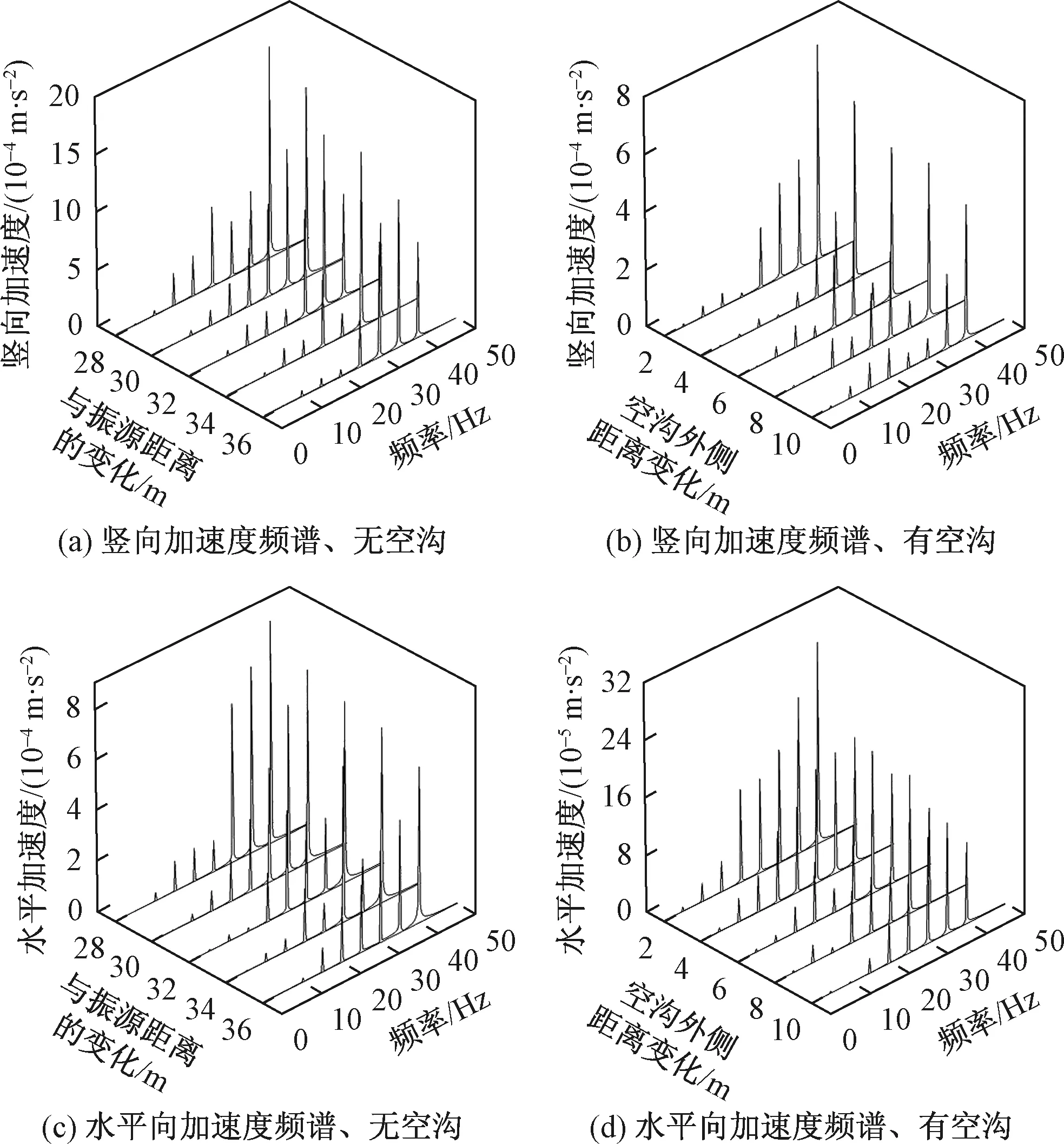
图10 有无空沟时土体振动加速度频谱对比
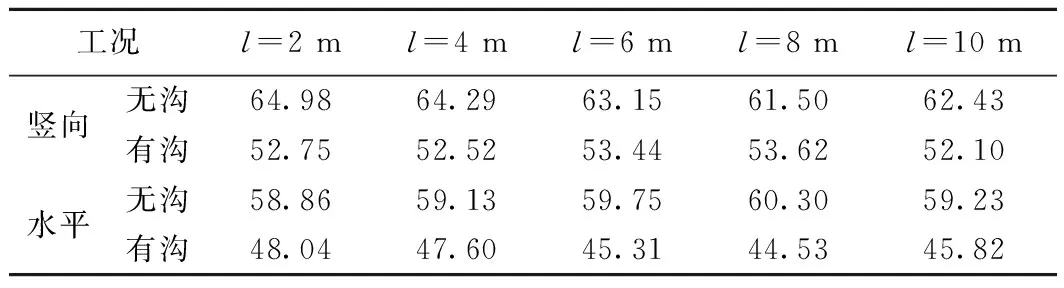
工况l=2 ml=4 ml=6 ml=8 ml=10 m竖向无沟64.9864.2963.1561.5062.43有沟52.7552.5253.4453.6252.10水平无沟58.8659.1359.7560.3059.23有沟48.0447.6045.3144.5345.82
(2) 振动频率相同时,不同位置处的竖向加速度频谱幅值均高于水平向加速度的频谱幅值。
(3) 空沟外侧拾振点随与沟外侧边缘距离逐渐增大,加速度幅值总变化趋势是降低的,但在空沟外侧边缘附近区域会出现振动加强现象。
(4) 随距空沟外侧距离的不断增加,土体振动的加速度振级总体走势不断降低;有空沟时,相应各点的加速度振级均小于无空沟时的振级。
3 结论
本文推导出瑞利波在空沟状况下的土体振动位移计算公式,并通过有无空沟的计算对比,得出以下结论:
(1) 空沟的埋置深度对空沟隔振效果的影响明显,随着空沟深度的增加,空沟外侧的土体振动衰减越多。
(2) 在同样的隔振效果条件下,随着频率的减小,空沟的深度应越来越深。
(3) 空沟外侧拾振点随与沟外侧边缘距离逐渐增大时,加速度幅值总的趋势是降低的。
(4) 有空沟的状况下,相应各点的土体竖向加速度振级、加速度频谱幅值及位移时程幅值均小于无空沟状况下的振级。

