应变硬化水泥基复合材料柱偏压性能研究

袁 方,陈梦成,周丰流

(华东交通大学 土木建筑学院，江西 南昌 330013)

混凝土拉伸脆性引起的开裂是钢筋混凝土(RC)结构中的主要耐久性问题，将导致腐蚀环境下RC结构中出现严重的钢筋锈蚀。解决锈蚀问题的一个潜在解决方案是用不锈蚀的纤维增强聚合物(FRP)筋材取代钢筋。然而，由于FRP材料弹性模量低及延性差，FRP筋的广泛使用受到一定程度的限制[1]。在钢筋混凝土结构中，由混凝土脆性引起的其他主要问题包括混凝土剥落、黏结劈裂以及钢筋与混凝土之间复合作用的丧失，这些问题均会削弱RC结构的延性和损伤容限能力[2-3]。

在过去的二十多年中，一种被称为工程水泥基复合材料(ECC)的高性能纤维增强水泥基复合材料已经开发并应用于基础设施工程[4-9]。ECC和混凝土的抗拉强度(4～6 MPa)和抗压强度(30～80 MPa)相似，但在拉伸荷载下的变形性能有显著差异。传统混凝土一旦开裂，便立即发生拉伸脆性破坏。然而，ECC初裂后，应力仍然随着变形的增加而增加，试件表面会出现大量的细密裂缝，直到最终发生裂缝集中现象而宣告破坏。一般来说，ECC的极限拉应变能够达到3%～5%，极限状态的裂缝间距为3～6 mm、裂缝宽度控制在60 μm左右[10]。现有的研究结果表明，ECC材料的剪切力学性能与单轴拉伸性能类似[11]。未配箍筋的FRP筋增强ECC梁较合理配箍的FRP筋混凝土梁表现出了更好的力学性能，表明ECC还能够起到类似箍筋的抗剪作用[12-13]。之前的研究还表明，ECC能与混凝土协调变形，从而降低了界面黏结应力并防止了纵向劈裂裂缝的出现[2]。Maalej等[14]指出，与相应的RC梁相比，在最终失效之前，在受拉侧设置ECC层的钢筋增强ECC-混凝土组合梁表现出更高的极限强度和宽度更小的裂缝。Chen等[15]提出将高强度ECC用于锈蚀钢筋混凝土结构的抗弯修复，结果表明，采用这种新技术能够有效弥补构件的抗弯强度，并且可以避免混凝土的大量凿除。往复荷载下钢筋增强ECC(R/ECC)受弯构件的试验研究也表明，当用ECC代替混凝土时，构件的耗能能力及损伤容限能力均能得到显著提升[3,16-17]。显然，由于ECC的独特性能，钢筋与ECC结合使用能够提高R/ECC受弯构件的延性和耐久性。

以往的研究主要集中在超高性能混凝土柱构件力学性能[18-19]和R/ECC构件的受弯性能，很少有关于R/ECC构件偏心受压力学性能研究的报道，因此有必要对这一问题进行深入研究。

本文将对6根R/ECC柱的偏心受压力学性能进行研究，主要研究纵筋配筋率和偏心距对R/ECC柱极限强度、延性和损伤容限等性能指标的影响。为了便于比较，还将对2根钢筋混凝土(RC)柱进行偏压试验研究。在试验结果的基础上，提出R/ECC柱荷载-变形响应的简化计算方法。最后，通过理论计算方法系统对比R/ECC柱与RC柱的承载力相关曲线。

1 试验概况

1.1 试件设计

本文共设计了8根柱试件，所有试件的截面尺寸均为b×d=200 mm×250 mm，柱高L均为1 200 mm。试验的柱构件可以分为两个系列，系列Ⅰ的4根柱构件的初始偏心距e0为40 mm，设计破坏模式为受拉钢筋未屈服前的基体压碎。系列Ⅱ的4根柱构件的e0为120 mm，设计破坏模式为钢筋受拉屈服后的基体压碎。系列Ⅰ和系列Ⅱ对应的偏心率(2e0/d)分别为0.32和0.96。每一个系列都包含了1根RC柱和3根R/ECC柱。每个柱构件都配置了4根直径相同的纵向钢筋，钢筋型号采用HRB400，直径分为3类，分别为12、16、20 mm；箍筋采用HRB335，直径和间距均为8、100 mm。表1列出了各试件的详细信息并用不同的编号加以区分，首字母E和C分别代表的是R/ECC柱和RC柱，第一个连号的阿拉伯数字代表的是钢筋的直径，第二个连号后的阿拉伯数字则代表的是初始偏心距。例如，编号为E-16-120的构件代表的是纵筋直径和偏心距分别为16 mm和120 mm的R/ECC柱。

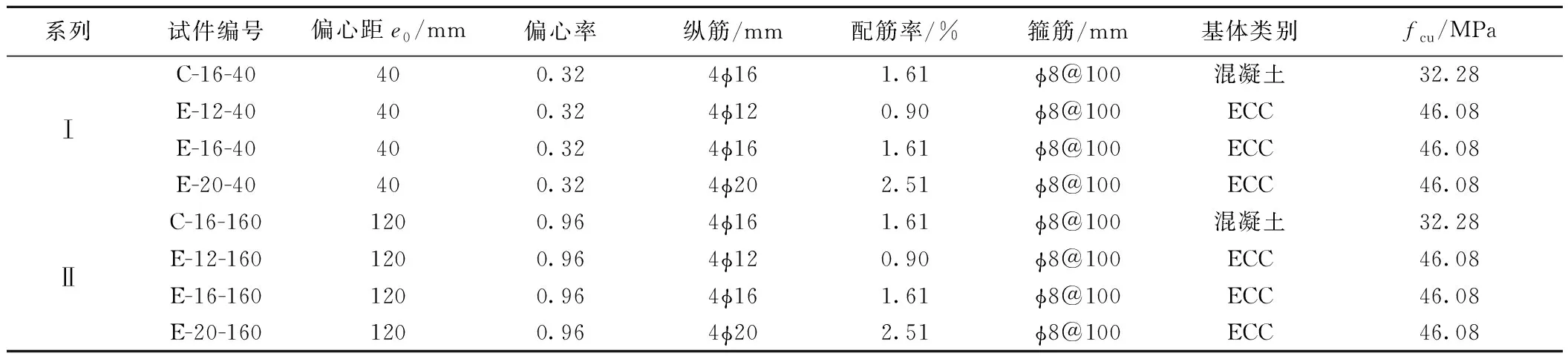
表1 试件信息表

1.2 材料性能

为了改善环境的可持续性，在ECC中采用了大量粉煤灰替代水泥，替代率高达80%。 ECC和混凝土的配合比列在表2中。为了评估ECC拉伸延性，对尺寸为350 mm×50 mm×15 mm的板件进行了单轴拉伸试验，典型的ECC拉伸应力-应变曲线如图1所示。从图1中可以看出，ECC拉伸强度超过了5 MPa，极限拉伸应变接近4%，表现出了良好的拉伸延性。此外，还浇筑了一批尺寸为100 mm×100 mm×100 mm的ECC和混凝土立方体试块，与构件同龄期同环境进行养护，并进行了单轴压缩试验，试验时间与柱试验同步。ECC和混凝土的实测立方体抗压强度分别为46.08 MPa和32.28 MPa。各直径钢筋的力学性能参数见表3。

表2 ECC和混凝土配合比

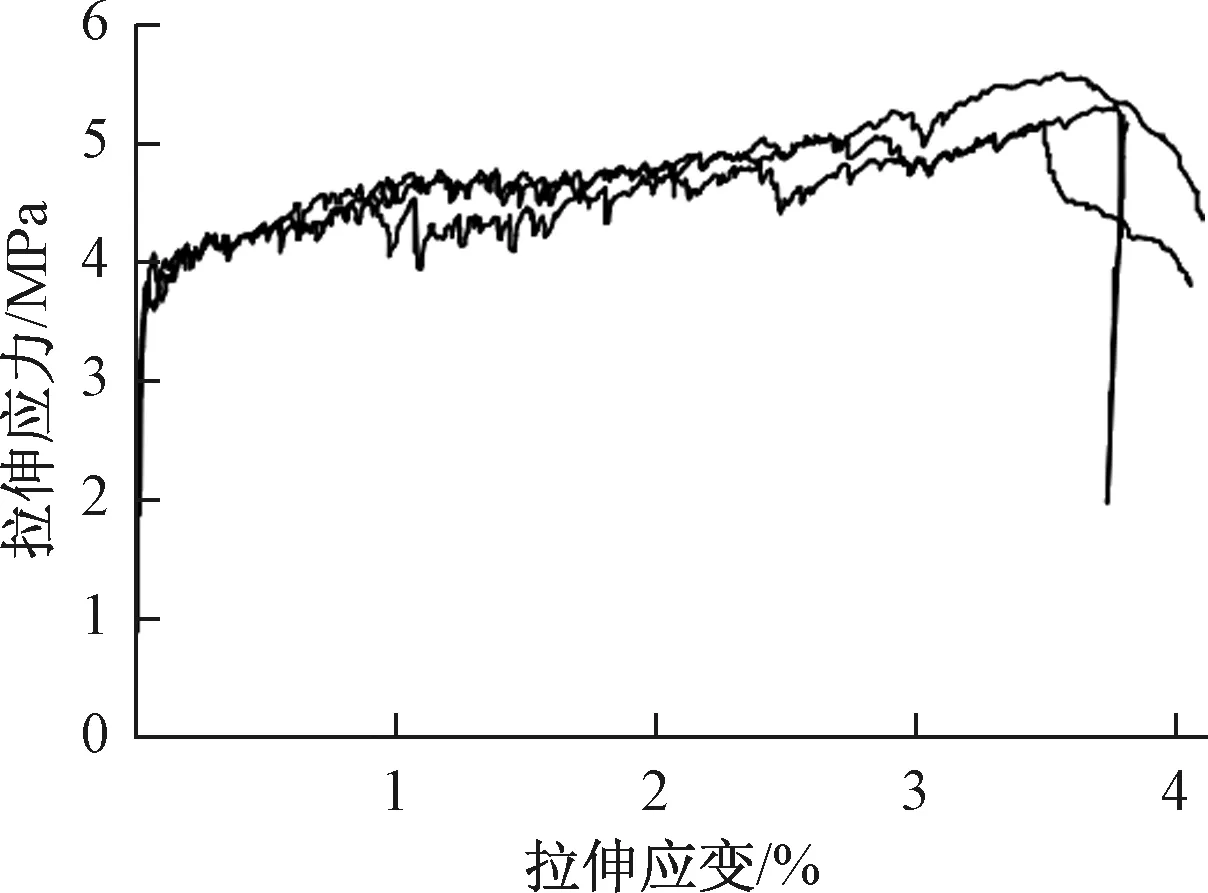
图1 ECC材料单轴拉伸应力应变曲线

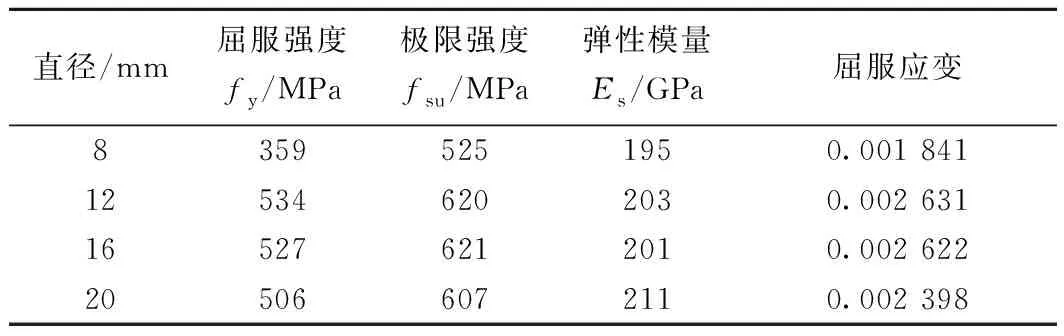
直径/mm屈服强度fy/MPa极限强度fsu/MPa弹性模量Es/GPa屈服应变83595251950.001 841 125346202030.002 631 165276212010.002 622 205066072110.002 398

1.3 加载方案

试件在5 000 kN的压力机下进行偏心受压试验。在试验机两端安装了厚度为20 mm的刀口铰，同时在试件两端设置了30 mm厚的加载板。加载板上按预定偏心距设置相应的条形凹槽，与刀口铰(20 mm厚)的刀口相吻合，以便精确控制加载偏心距。在试件高度方向设置了三个位移传感器以观测柱构件的侧向挠度。在试验机上下加载板上分别安装了1个位移传感器以测量试验期间的纵向压缩量。在纵向上设置了5个间距为100 mm的应变片，同时在柱中部截面混凝土表面上设置了6个间距为50 mm的应变片，测点布置见图2。试验采用分级加载制度，在达到峰值荷载之前，加载间隔为预估承载力的1/15，每级荷载保持大约2 min。在达到峰值荷载之后，加载速率变缓，直到构件发生最终破坏。试验过程中所有测量数据都由数据采集仪自动采集。

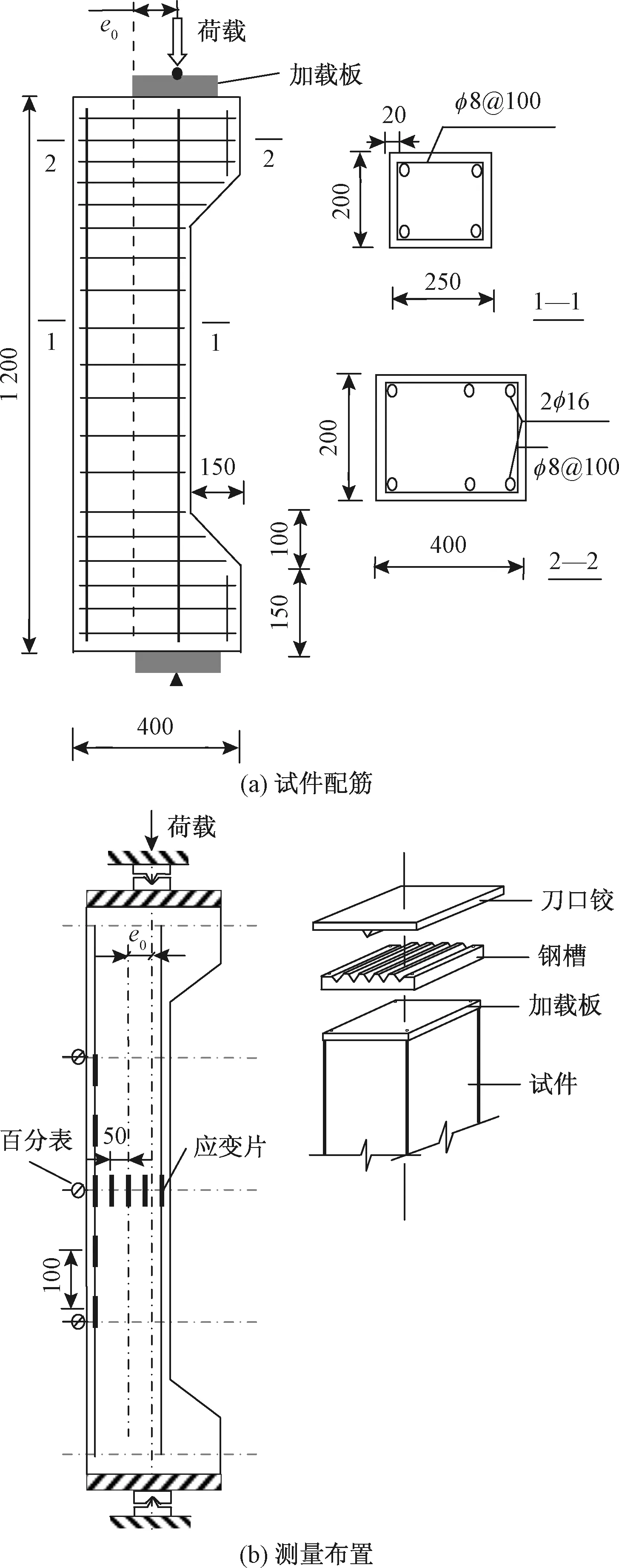
图2 试件配筋及测量信息(单位：mm)

2 试验结果与分析

2.1 破坏形态和裂缝模式

各试件的破坏形态见图3，从图3中可以看出，每个构件都因受压侧基体压碎而宣告破坏，均为受压破坏，并且由于边界条件的影响，ECC或混凝土的局部压碎区域靠近构件的上端。虽然构件均因基体压碎而达到极限状态，但是R/ECC柱和RC柱的破坏形态有很大差异。RC柱破坏时刻出现了明显的混凝土剥落现象，而R/ECC柱由于ECC的纤维之间的桥联作用并未出现ECC剥落现象。这说明相比于混凝土，ECC能够为纵向钢筋提供更有效的侧向约束，从而延迟钢筋的屈曲以及改善构件的损伤容限能力。

图3 试件破坏形态

各试件的最终开裂模式见图4。对于初始偏心距为40 mm的试件，初始开裂荷载大约为峰值荷载的30%；对于初始偏心距为120 mm的试件，初始开裂荷载大约为峰值荷载的15%。初始偏心距越大，弯曲荷载就越大。弯曲裂缝首先出现在远离轴向力的一侧，并且随着荷载的增加不断向靠近轴向力的一侧延伸。对于偏心距为120 mm的R/ECC柱，裂缝的集中开展出现在峰值荷载后，而对于偏心距为40 mm的R/ECC柱，整个加载过程中均未出现裂缝集中现象。从试验现象中还可以发现，在极限状态下，R/ECC柱的受拉侧出现了近百条细密裂缝，而对于RC柱受拉侧仅出现了不足10条的弯曲裂缝。这说明将ECC替代混凝土能够显著减小裂缝宽度，从而提高偶然荷载后不能即刻修复的柱构件的耐久性。

图4 试件最终开裂模式

偏心距为120 mm的柱构件最大裂缝宽度随偏心荷载(N)增加的发展曲线见图5。对于RC柱，裂缝宽度随着荷载的增加呈线性增长，并且峰值荷载下对应的最大裂缝宽度达到了2 mm；相比之下，随着荷载的增加，R/ECC柱的最大裂缝宽度先增长后基本维持在60 μm保持不变。这一显著的裂缝宽度发展差异归因于ECC和混凝土这两种材料迥异的裂缝开展进程。混凝土一旦达到拉伸强度，裂缝宽度便迅速增长。而ECC在初裂后，拉伸荷载能够伴随着多裂缝的开展继续上升。每一条裂缝都开展到一定的裂缝宽度后保持稳定，而继续增加的变形将导致新的裂缝继续出现，直至在裂缝宽度在一条裂缝上集中开展而达到开裂饱和状态。

图5 峰值荷载前最大裂缝宽度随挠度变化曲线

2.2 荷载-挠度曲线

各试件的荷载-跨中挠度曲线见图6。由图6可知，在峰值荷载前，挠度随着荷载的增加迅速增长。峰值荷载后，荷载随着挠度的增加而下降，直至混凝土和ECC发生压碎失效。RC柱承载力的下降幅度要大于R/ECC柱，这主要因为ECC的极限压应变约为混凝土的2倍[20-21]，从而使得R/ECC受弯构件具有更好的延性。由图6可知，极限强度随着配筋率的增加而增大，并且R/ECC柱的极限强度要高于同等配筋情况下的RC柱。和RC柱相比，偏心率分别为40 mm和120 mm的R/ECC柱较RC柱分别提升了35.6%和31.8%。由于ECC的抗压强度要高于混凝土，因此很难判断是否有除抗压强度外的其他原因造成R/ECC柱更高的极限强度，将在下一节的参数分析中具体讨论。

由于混凝土的弹性模量要远大于ECC，在强度相同的情况下，R/ECC柱峰值荷载对应的位移应大于RC柱。图6中RC柱峰值荷载点对应的位移接近甚至大于R/ECC柱主要是由于两方面的原因造成的：一是混凝土的抗压强度要远低于ECC，使得ECC的弹性模量大于混凝土；二是混凝土开裂后承载力立即丧失，而ECC开裂后始终能为ECC提供稳定拉力，导致R/ECC柱刚度进一步提升，刚度大则变形能力会相应削弱，从而导致RC柱和R/ECC柱在峰值荷载下对应的位移相近。

2.3 应变分析

纵筋直径为16 mm的柱构件混凝土应变沿截面高度的变化规律见图7。由图7可知，在整个加载过程中，混凝土应变几乎沿着截面高度线性分布，这说明基本符合平截面假定。在每一个荷载水平下，偏心距为40 mm的柱构件的受压区高度均显著大于偏心距为120 mm的构件。

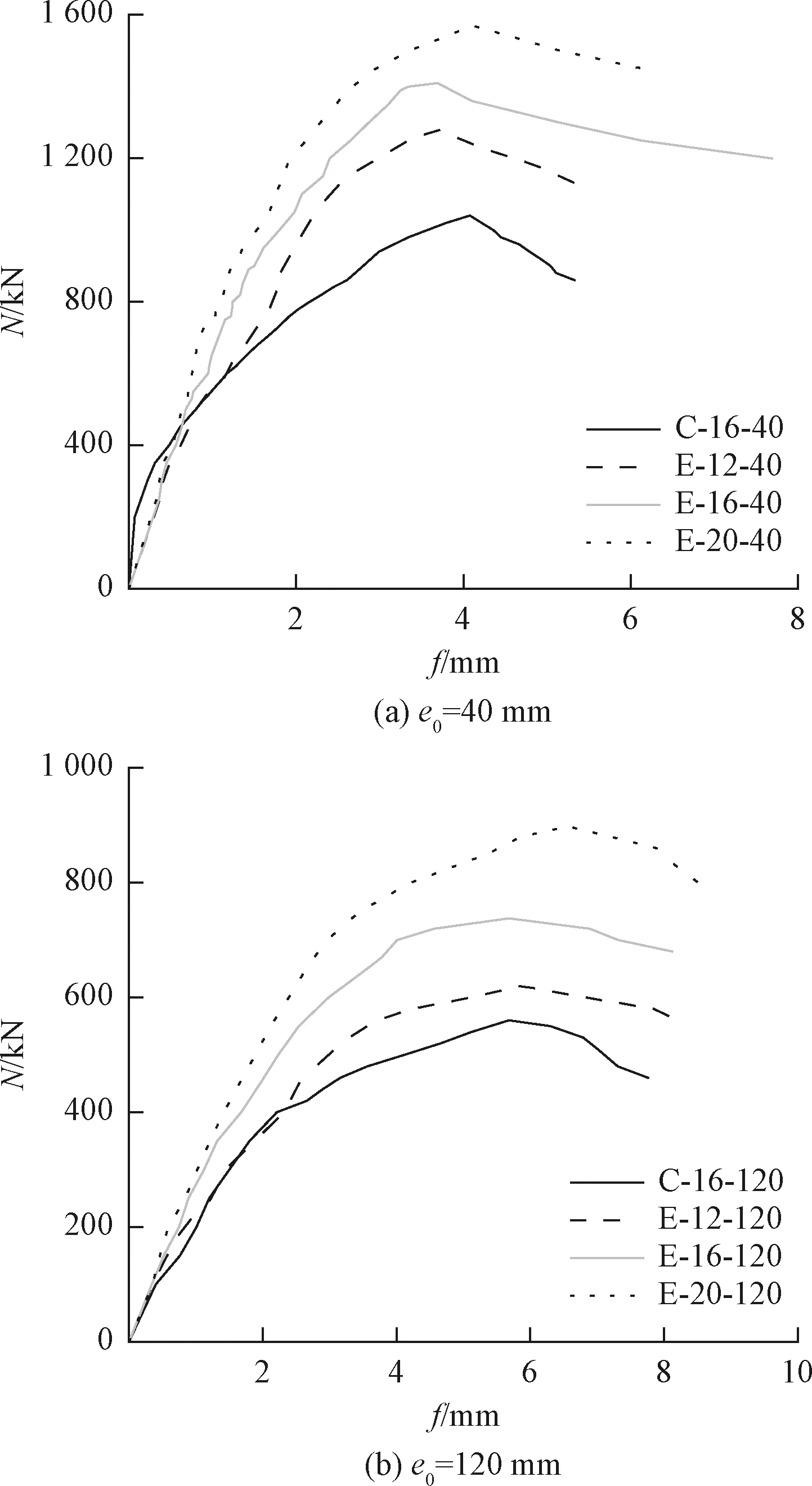
图6 试件荷载-跨中挠度曲线

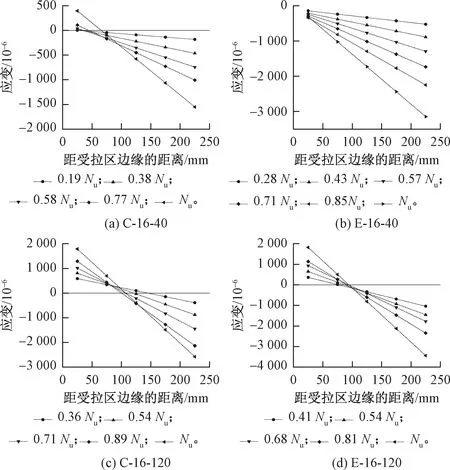
图7 混凝土应变沿截面高度变化规律

各荷载水平下，构件C-16-120和E-16-120纵筋应变的发展规律见图8。不难看出，RC构件纵筋应变的波动要大于同等配筋下的R/ECC柱。对于试件C-16-120，混凝土一旦开裂，拉力便几乎全由钢筋来承担，造成开裂截面钢筋应变的突然增大(跨中以上100 mm处及跨中以下200 mm截面处)。相比之下，试件E-16-120开裂后，ECC裂缝截面拉应力仍然能由纤维继续传递，使纵筋应变分布更为均匀。

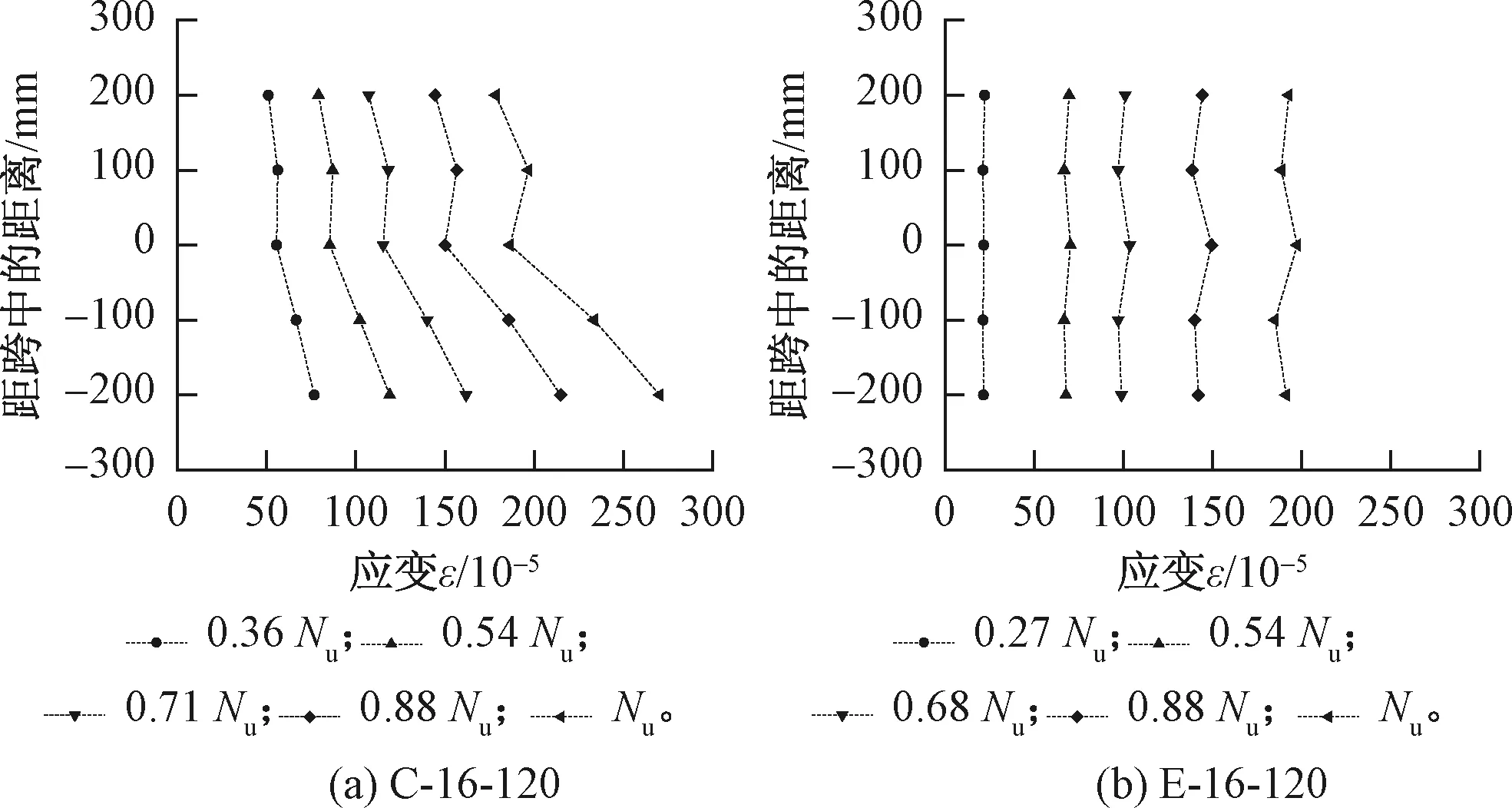
图8 钢筋应变沿长度方向变化规律

3 理论分析

3.1 理论建模

由上述试验结果中可以得知，混凝土应变几乎沿截面高度线性分布，因此本理论计算采用了平截面假定。ECC的本构模型是采用的Yuan等[22]提出的模型，见图9(a)。在拉伸荷载下，ECC开裂后进入拉伸硬化阶段，直至集中裂缝出现后应力降至0。ECC的应力-应变关系由双折线为

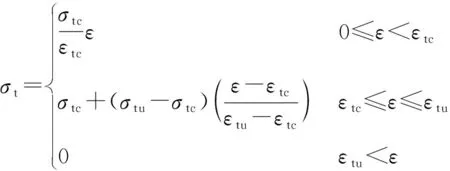
(1)

式中：σtc和εtc分别为ECC的初裂应力和初裂应变；σtu和εtu分别为ECC的极限应力和极限应变。在压缩荷载作用下，ECC的应力-应变曲线由非线性上升段和双折线下降段组成，可表示为

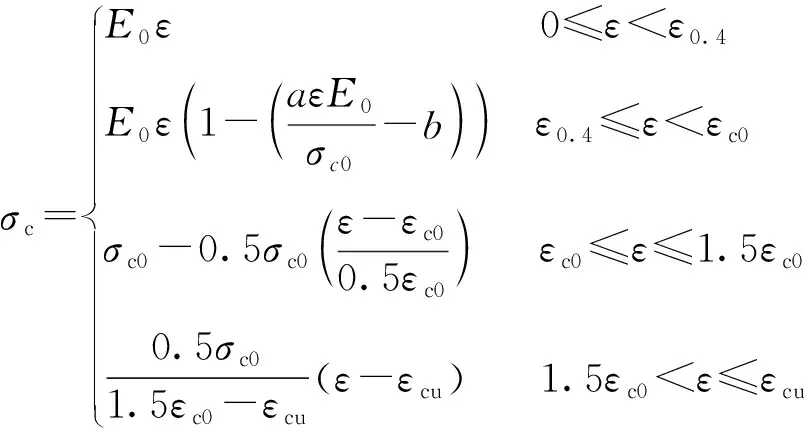
(2)

式中：E0为ECC的弹性模量，E0=1.5(σc0)0.638[21]；ε0.4为0.4倍抗压强度对应的应变；a和b的取值分别为0.308和0.124[21]；σc0和εc0分别为ECC峰值应力和对应的应变；σcu和εcu分别为ECC的极限应力和极限应变。

本计算中忽略了混凝土的抗拉作用。峰值应力前混凝土的受压应力-应变关系采用的是Hognestad等[23]提出的模型，之后便线性下降直至应力为0，见图9(b)。完整的应力-应变曲线可表示为

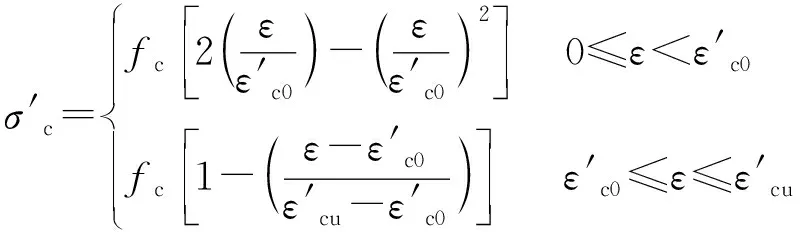
(3)

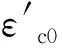
钢筋采用的是具有拉伸硬化段的弹塑性双折线模型，见图9(c)，应力-应变关系可表示为

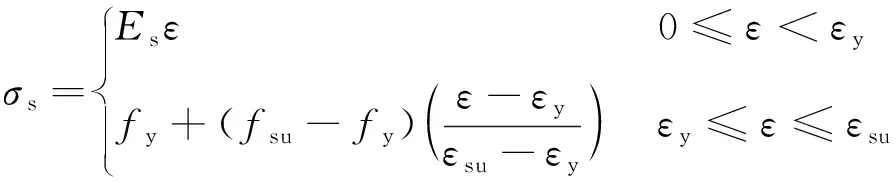
(4)

式中：Es为钢筋的弹性模量；fy和εy分别为钢筋的屈服强度和屈服应变；fsu和εsu分别为钢筋的极限强度和极限应变。

本文通过牛顿-科特斯积分方法对构件截面的荷载-变形曲线进行计算。使用的运算软件是Matlab，首先假定一个初始偏心距e0和受压侧边缘纤维的应变εc，受压区高度c便可以通过假定的材料应力-应变关系和截面弯矩平衡表达式来进行计算。截面曲率可以通过εc与c的比值来获得，而轴向力可以通过沿截面高度方向的应力积分来获得。由于试验得到的跨中挠度值远小于初始偏心距，见图6，因此，本计算模型中忽略了因柱弯曲变形所引起的附加弯矩。通过不断变化εc，便可计算得到构件的弯矩(荷载)-跨中截面曲率曲线，直至εc达到材料的极限压应变值终止计算。从荷载-曲率曲线中可以获取各柱构件的峰值荷载。通过强度收敛性分析可以得知，当εc的增量取为0.000 1时，构件承载力的误差将小于0.5%。

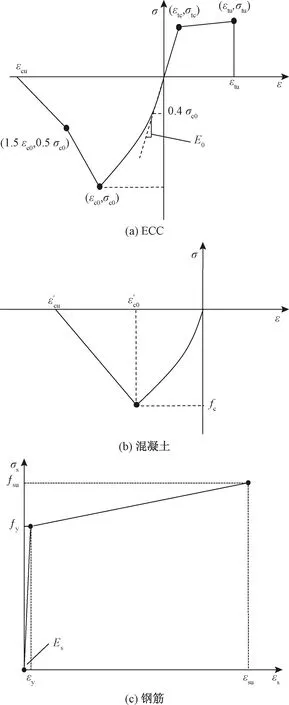
图9 材料应力-应变关系

表4 数值模拟中混凝土和ECC的材料性能参数

3.2 试验结果与计算结果的对比

为了评估计算方法和材料本构模型的可靠性，对本文实测的8根柱构件的承载力进行了计算。各试件计算承载力与实测承载力的对比见图10，由图10可知，实测结果与计算结果吻合良好。本文还通过误差分析对模型的准确性进行了定量分析，承载力预测的误差可通过下式进行计算为

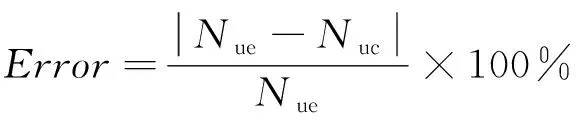
(5)

式中：Nue和Nuc分别为实测承载力和计算承载力。通过计算可知，通过理论模型计算得到的承载力的平均误差、标准差和最大误差分别为1.55%、1.28%和4.45%，再次证明了本计算方法的准确性。

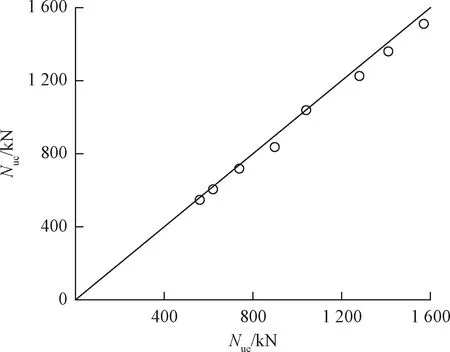
图10 试验和模拟所得到的极限强度对比

3.3 RC柱与R/ECC柱承载力相关曲线对比

为了全面评估R/ECC柱的承载力，对R/ECC柱的正截面受压承载力-受弯承载力(Nu-Mu)相关曲线进行了计算，并与RC柱进行了对比。通过3.1节所描述的方法，不断变换初始偏心距e0，便可得到各构件的承载力相关曲线。所选取的基准构件的参数如下：构件截面尺寸b×d=400 mm×400 mm，柱侧边缘距纵筋合力作用点的距离为40 mm；4根纵向钢筋的直径均为25 mm。参照ECC在单轴应力-应变曲线试验数据[21-24]。ECC和混凝土的材料性参数见表4。钢筋的弹性模量、屈服强度、极限强度和极限应变分别取为200 Gpa、460 MPa、600 MPa和0.1。

图11为RC柱和R/ECC柱Nu-Mu承载力相关曲线的对比。从图中11可以看出，R/ECC柱的承载力相关曲线的变化规律与RC柱类似，受压承载力随着偏心距的增大不断减小，而受弯承载力则随着偏心距的增大先增大后减小。另外，由图11可知，当偏心率很小时，R/ECC柱的承载力与RC柱的承载力非常接近；而当偏心率很大，R/ECC柱的承载力要明显大于同等条件下的RC柱。这可以通过以下机理加以解释。当偏心率很小时，弯矩与轴向力的比值很小，此时大部分的截面积处于受压状态。因此，ECC的高延性拉伸特性对整个柱承载力的贡献十分有限。当偏心率很大时，弯矩与轴向力的比值相应变大，此时处于受拉状态的截面积也相应增大。在这种情况下，ECC的超高韧性特性便能够充分发挥出来，ECC的抗拉贡献相当于提高了纵向受拉钢筋的配筋率。众所周知，纵向受拉钢筋的配筋率越大，需要平衡总拉力的基体压力越大，从而抗弯强度也越大。因此，当偏心水平很高时，R/ECC柱的承载力要显著高于RC柱。

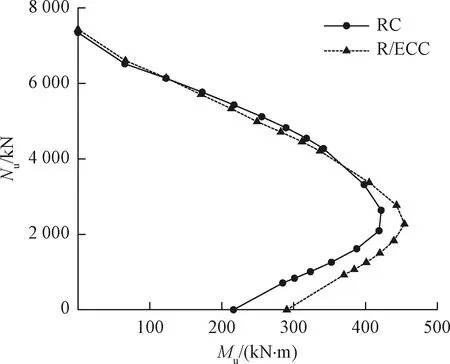
图11 RC柱与R/ECC柱承载力相关曲线对比

4 结论

本文对R/ECC和RC柱在偏心受压荷载下的力学性能进行了研究。首先，对6根R/ECC柱和2根RC柱进行了偏心受压试验。其次，通过理论分析计算了R/ECC柱的峰值承载力，并与试验结果进行了对比。最后，通过参数分析对比了R/ECC柱和RC柱的正截面受压承载力-受弯承载力(Nu-Mu)相关曲线。主要结论如下：

(1)R/ECC柱的破坏形态与RC柱有显著不同。虽然R/ECC柱和RC柱最终都因基体压碎而宣告失效，然而，RC柱最终出现了严重的基体剥落现象；相比之下，R/ECC柱由于ECC的纤维桥梁作用，整个加载过程均未出现ECC剥落现象。

(2)R/ECC柱的裂缝控制能力要明显优于RC柱。RC柱的最大裂缝宽度随着荷载的增加线性增长，并在峰值荷载前达到了2 mm。R/ECC柱的最大裂缝宽度先随着荷载的增加而增加，随后基本维持在60 μm保持不变。

(3)由于ECC较混凝土更大的极限压应变，R/ECC柱的延性要优于同等配筋条件下的RC柱。

(4)通过Nu-Mu承载力相关曲线的参数分析可知，当偏心水平较低时，R/ECC柱的承载力与RC柱的承载力差别不大，而在同等条件下，当偏心水平很高时，R/ECC柱的承载力要明显大于RC柱。