铁路主隧道与斜井风流耦合作用下的火灾模型试验研究

李 琦,王明年,李自强,于 丽,严 涛，谢文静

(1.四川农业大学 建筑与城乡规划学院，四川 都江堰 611830；2.西南交通大学 土木工程学院，四川 成都 610031；3.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；4.重庆科技学院 建筑工程学院，重庆 401331)

我国是多山国家，随着铁路交通网覆盖面的扩大，穿山铁路隧道里程逐年增加，长大铁路隧道(长度大于10 km)数量更是迅猛增长。长大铁路隧道内空间狭长且相对封闭，可供人员疏散的出口有限，一旦发生火灾，隧道内环境会迅速升温并充满烟气，可造成大量的人员伤亡以及财产损失。铁路隧道内发生火灾并停车疏散的情景，主要分为两类：一类是定点停车疏散，即在紧急救援站进行停车疏散，此时，救援站内一般设置有较完备的控烟措施，疏散通道数量多且集中，但紧急救援站的设置间距一般为20 km，数量较少；另一类就是随机停车，即在斜井、横洞、联络横通道等紧急出口处进行停车疏散，由于通风设备配置简单、出口数量仅为1～2个，疏散安全成为主要问题。因此，国内外学者在长大铁路隧道防灾救援方面进行了大量的研究。

文献[1]进行隧道的火灾燃烧原型试验，对不同种类物质燃烧时隧道内烟气层高度以及温度的分布规律进行研究，并给出了隧道火场内CO气体的分布情况。文献[2]通过隧道火灾的缩尺模型试验，研究不同火灾规模、不同风速条件下火场的温度及烟气分布，得到了与火源距离增加隧道内沿程温度的衰减规律。文献[3]进行全尺寸的隧道火灾燃烧试验，将以不同比例混合的燃料作为火源，研究隧道内烟气温度、厚度等参数的变化规律，并建立了隧道顶棚温度随火灾发展的衰减模型。文献[4]通过隧道火灾缩小比例模型试验得到火源上下游烟流蔓延长度与通风速度的关系并提出了理论模型。文献[5]采用1∶9的缩尺模型，进行不同火源释放率条件下的隧道火灾燃烧试验，探究不同火源条件下隧道内温度的分层规律，获得火源面积、通风条件等参数对隧道内温度的抑制作用表现。文献[6]进行1∶50的隧道火灾缩尺模型试验，对竖井不同通风模式下隧道内火场的温度、烟流规律进行研究，提出火灾情况下隧道内的风流组织控制方法。文献[7-8]对隧道火灾的温度、烟气分布规律进行大量研究，同时对火灾时人员疏散及救援方面也做了许多研究。

综上可知，在众多铁路隧道火灾研究中，关于斜井对主隧道内火灾温度分布、烟气蔓延等影响的研究并不多，而斜井作为紧急出口时，需要向主隧道通风以保证主隧道内人员的氧气需求并产生防烟作用，因此，研究斜井气流对主隧道火灾环境的影响，对预测人员在随机停车情况下的安全性以及完善铁路隧道防灾救援设计都具有现实意义。

1 隧道火灾模型试验系统

1.1 模型相似比

1.1.1 相似准则

受限空间火灾模拟多采用弗劳德尺度准则[9-10]。欲使模型和原型满足流体动力相似，则必须保证两者的弗劳德数相等。定义弗劳德数

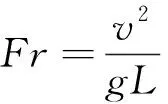
(1)

式中：v为流速；g为重力加速度；L为定性长度。

利用弗劳德尺度准则得到缩尺模型与原型间的尺度关系如表1所示，表1中下标m表示缩尺模型，p表示原型。

表1 弗鲁德模型缩尺关系

1.1.2 相似比确定

要实现模型与实际隧道内空气的流动相似，流动雷诺数(Re)一般要大于105 [11]，即

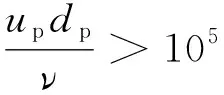
(2)

umdmν>105

式中：u为特征风速，m/s；d为当量直径，m；ν为流体运动黏性系数，m2/s。

1.2 试验装置

1.2.1 模型参数

(1)模型主材选择

隧道壁由热轧钢板(4 mm和2 mm)+防火玻璃(厚12 mm)/亚克板(厚10 mm)制作，见图1。考虑到试验实际情况，在火源附近使用4 mm厚热轧钢板，其余部分使用2 mm厚热轧钢板，其主材钢板的选取满足隧道壁面沿程摩阻系数范围的规范要求[12]。

图1 隧道材料示意(单位：m)

(2)模型长度确定

隧道模型长25 m[12]，由10节拼装组成，每节长2.5 m,见图2。

(3)模型横断面尺寸

模型隧道主隧道断面为马蹄形，宽度0.9 m，高度0.65 m，坡度2%，见图3。斜井断面为矩形，宽度0.5 m，高度0.35 m，长度6 m，坡度12%。含斜井的隧道现场模型见图4。

图2 隧道组成示意 (单位：m)

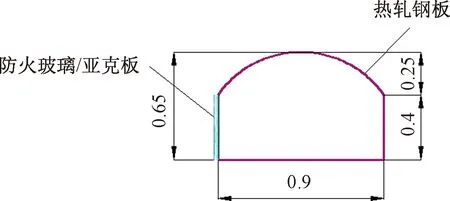
图3 主隧道横断面示意(单位：m)

图4 隧道现场模型

1.2.2 火源参数

模型采用油池火模拟火源，主要燃烧物质为乙醇。油盘尺寸决定火源的热释放速率，采用燃烧失重法计算火源的热释放速率，根据文献[13-14]的油盘尺寸试验结果，得到油池盘尺寸与火源热释放速率的关系，见图5[12]。

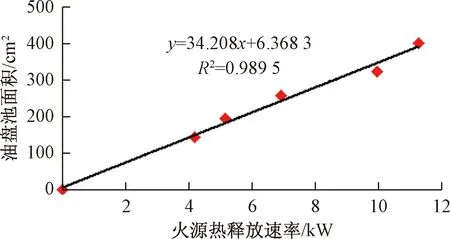
图5 油盘池面积与火源热释放速率关系

由图5可知，燃烧拟合曲线为

A=34.208Q+6.3683

(4)

式中：A为油池面积，cm2；Q为火源热释放速率，kW。

由式(4)得到试验油池盘的尺寸，如表2所示。

表2 试验油池盘尺寸

1.3 采集设备

本次试验采用TST 3826E拟静态数据采集系统(2台共120个采集信号通道)，温度测量选用插入式铠装热电偶，测试范围选择0～500 ℃和0～1 200 ℃两种。

1.4 测点布置

主隧道纵向布置10个烟气温度测试断面(ZW1～ZW10)，每个断面有5个测点，其中每个断面在拱顶位置布置1个测点，除各断面拱顶共布置的10个测点外，主隧道顶部另布置31个测点，即主隧道拱顶共布置41个测点(Z1～Z41)；斜井内设置2个温度测试断面(XW1、XW2)，每个断面有3个测点；共计87个温度测点。温度测点布置见图6、图7，温度传感器布置见图8。

1.5 测试工况

通过不同的火灾规模(15 MW、20 MW)、斜井风速(不通风、1 m/s、2 m/s、3 m/s)、主隧道风速(不通风、2.5 m/s)的组合，共进行了16组试验，主隧道坡度为2%，斜井坡度为12%。具体工况如表3所示。

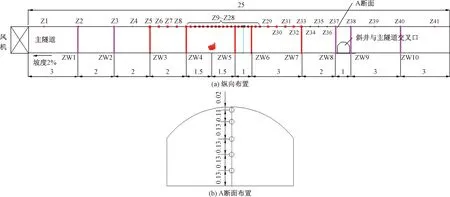
图6 主隧道内温度测点布置(单位：m)

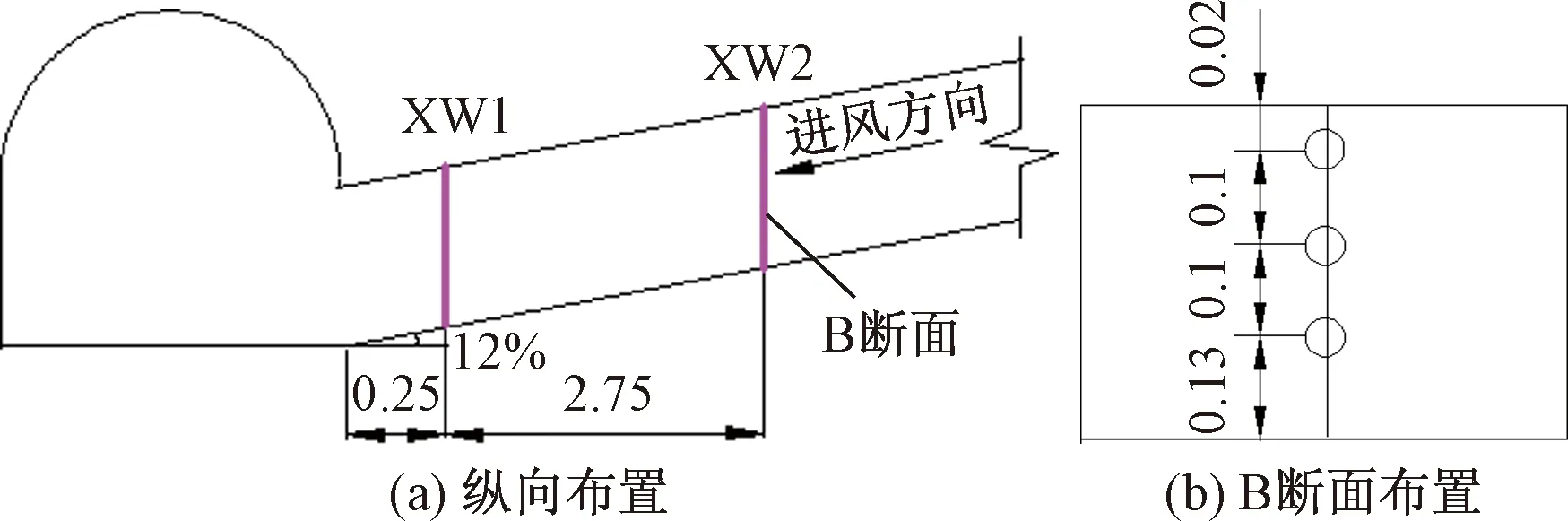
图7 斜井内温度测点布置(单位：m)

图8 温度传感器布置

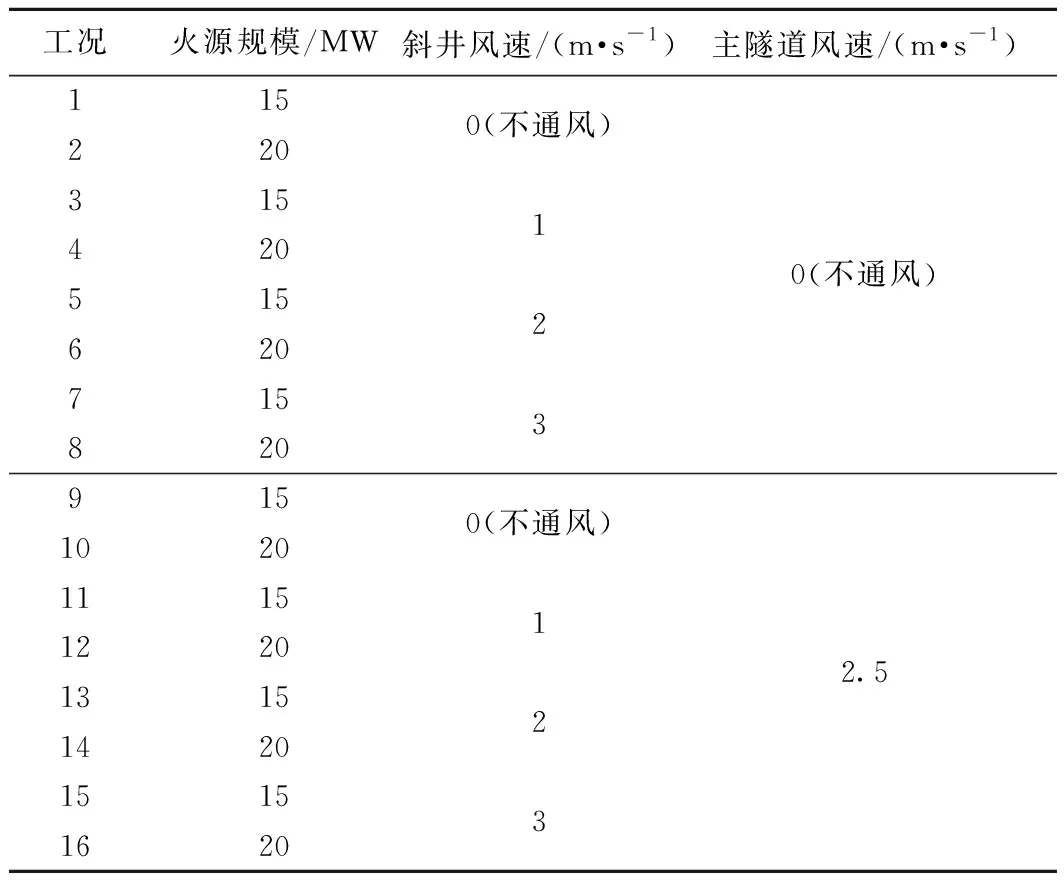
工况火源规模/MW斜井风速/(m·s-1)主隧道风速/(m·s-1)1150(不通风)22031514200(不通风)515262071538209150(不通风)10201115112202.5131521420151531620

2 隧道火灾模型试验结果分析

2.1 主隧道温度变化

2.1.1 隧道升温规律

火灾规模为20 MW时，燃烧持续15 min，火源上方拱顶处温度随时间变化曲线见图9，试验现场见图10、图11。

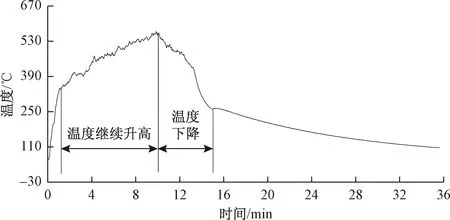
图9 火灾规模20 MW的拱顶温度曲线

图10 主隧道

图11 火源

由图9可知，在火灾开始几十秒内，主隧道内拱顶温度急速上升，由30 ℃升至330 ℃，在第10 min达到最高温度，约580 ℃，随后火源温度衰减过程大约持续5 min，温度降至250 ℃，最后温度缓慢降低。

2.1.2 火灾规模对温度的影响

主隧道不通风条件下，提取火灾规模为20 MW和15 MW时主隧道拱顶的温度变化曲线，二者对比见图12。其中，横坐标零点代表火源位置，横坐标取正值代表有斜井段，横坐标取负值代表不含斜井段，下文同。

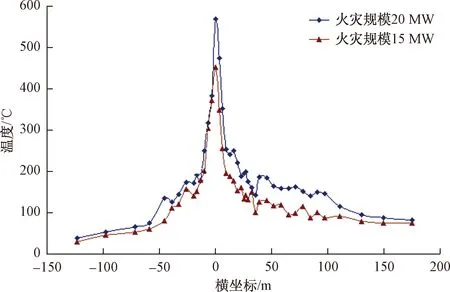
图12 不同火灾规模下主隧道拱顶的温度曲线

由图12可知，主隧道不通风时，拱顶温度变化较对称，火源处温度最高，火源两侧温度逐渐降低，且主隧道上坡方向温度大于下坡方向。随着火灾规模的增大，火源上方拱顶最高温度升高。火灾规模为20 MW和15 MW时，主隧道拱顶最高温度分别为580 ℃和450 ℃。

2.1.3 主隧道风速对温度的影响

火灾规模为20 MW时，分别提取主隧道内不通风和风速2.5 m/s两种工况下的主隧道拱顶温度，两条变化曲线对比见图13。

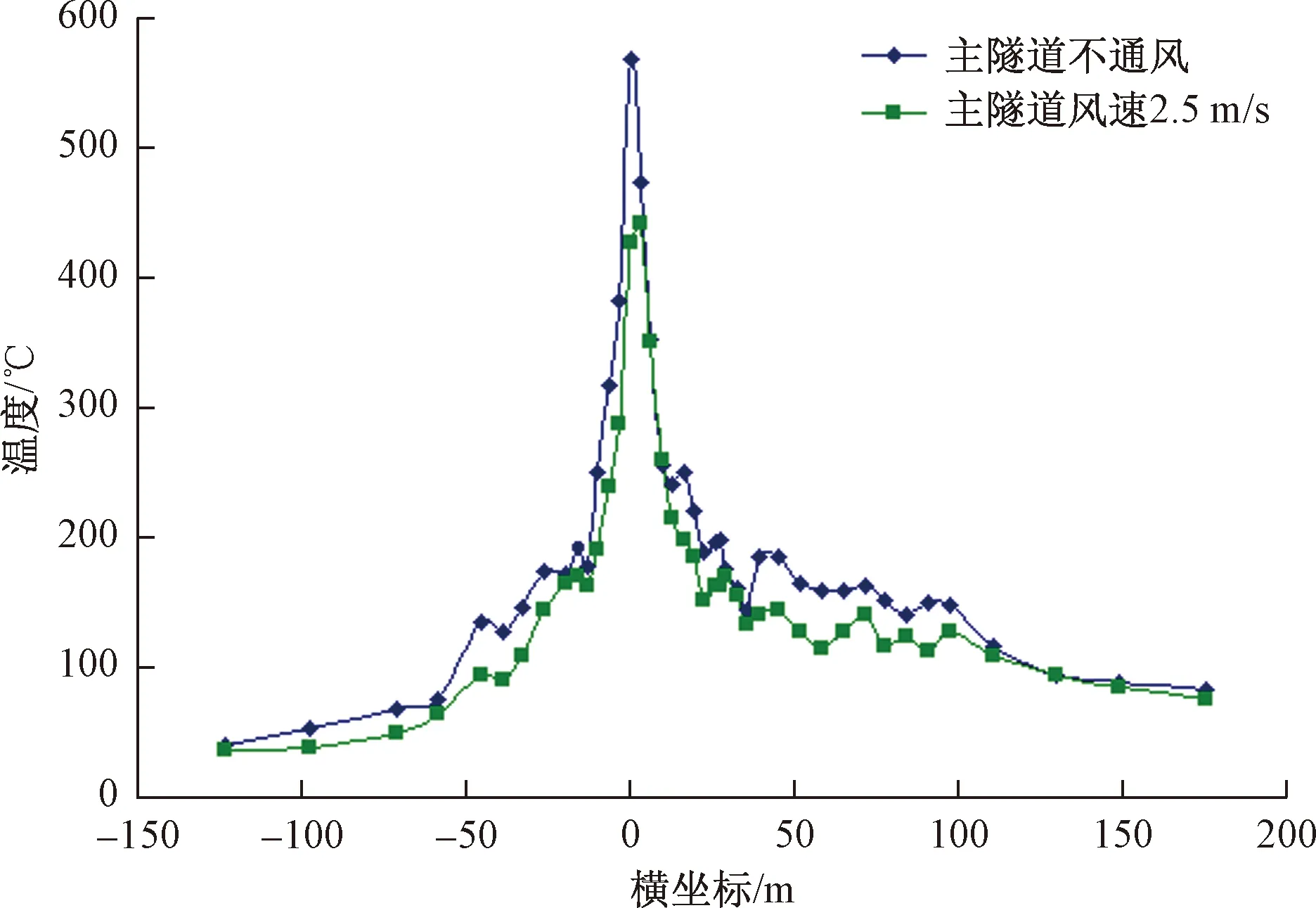
图13 不同主隧道风速下主隧道拱顶的温度曲线

由图13可知，主隧道内通风时的拱顶温度低于不通风工况。主隧道内不通风和风速2.5 m/s时，拱顶最高温度分别为580 ℃和440 ℃。

2.1.4 斜井风速对温度的影响

火灾规模为20 MW条件下，主隧道内不通风时，分别提取斜井不同风速(不通风、1 m/s、2 m/s、3 m/s)时主隧道拱顶温度，4条温度变化曲线对比见图14。

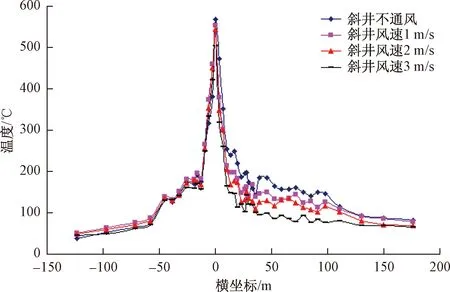
图14 不同斜井风速下主隧道拱顶的温度曲线

由图14可知，斜井向主隧道内送风的风速越大，带有斜井主隧道段内的拱顶温度越低，风速对不带有斜井主隧道段温度的影响较小。火源处最高温度随斜井送风风速的增加而降低。斜井不送风和送风风速1、2、3 m/s时，主隧道内拱顶的最高温度分别达到580、560、540和500 ℃。

2.2 斜井烟流长度的变化

2.2.1 斜井风速对烟流长度的影响

火灾规模为20 MW条件下，提取不同风速(不通风、1 m/s、2 m/s、3 m/s)时斜井内的烟气蔓延长度，4条变化曲线对比见图15，斜井烟气蔓延的试验现场见图16、图17。

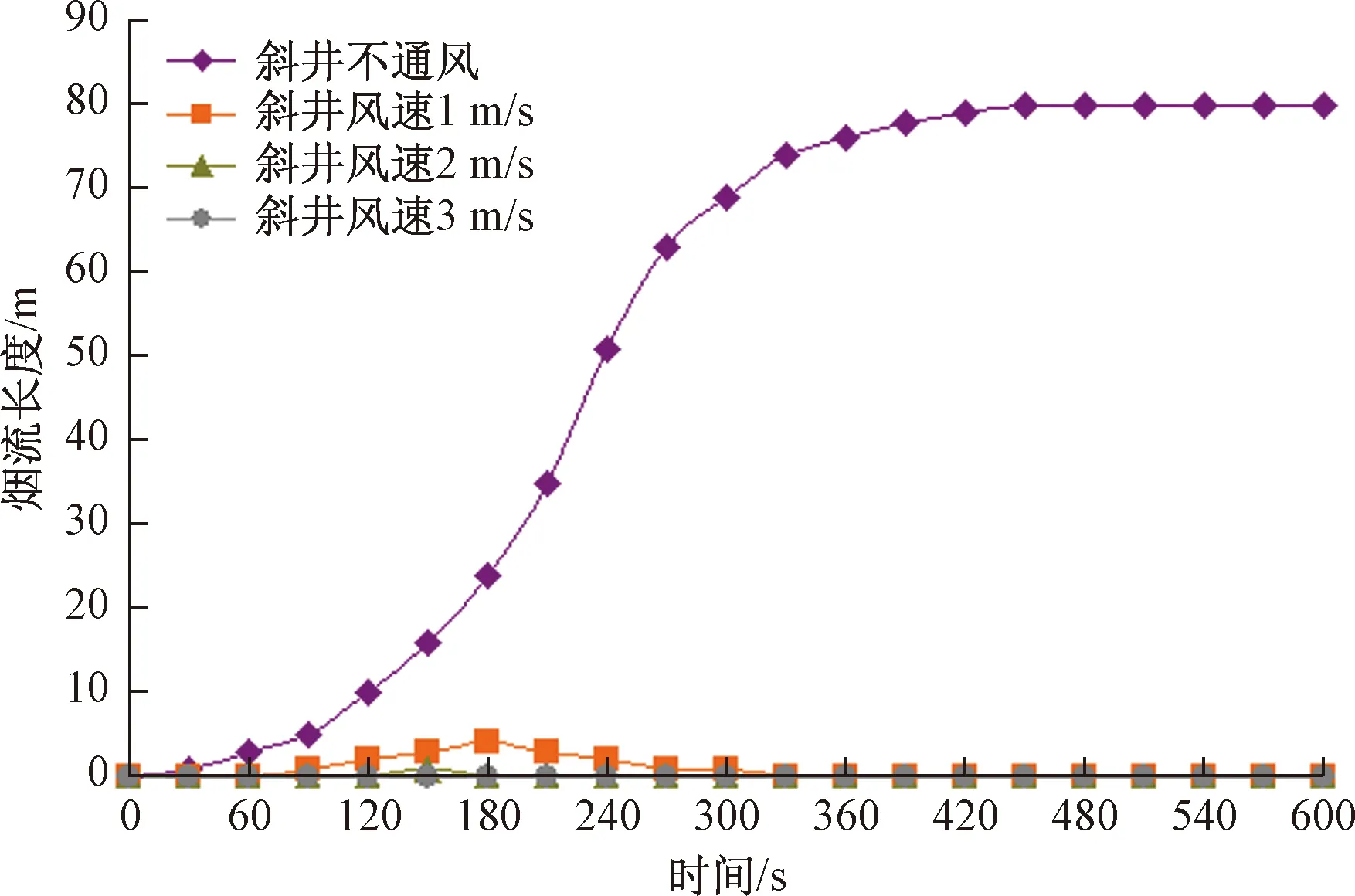
图15 不同斜井风速下的斜井内烟流长度曲线

图16 斜井内烟流扩散情况

图17 斜井出口烟气蔓延情况

由图15可知，烟气在斜井内的蔓延长度随斜井送风风速的增大而减小。由图16可知，斜井内的火灾烟气呈现出明显的分层现象，上部烟气浓度大且扩散速度快，下部烟气浓度小且扩散速度慢。当斜井不向主隧道送风时，450 s时火灾烟气的实际蔓延长度为78 m；当斜井风速为1 m/s时，在180 s时火灾烟气的实际蔓延长度为4 m；当斜井送风风速为2 m/s时，火灾烟气基本不进入斜井内；当斜井送风风速为3 m/s时，无烟气进入斜井。因此可知，若将斜井设置为紧急出口，确保火灾烟气不进入斜井的临界风速为2 m/s。

2.2.2 主隧道风速对烟流长度的影响

火灾规模为20 MW、斜井不通风条件下，提取主隧道不通风和通风风速2.5 m/s时的斜井内火灾烟气蔓延长度，二者变化曲线对比见图18。

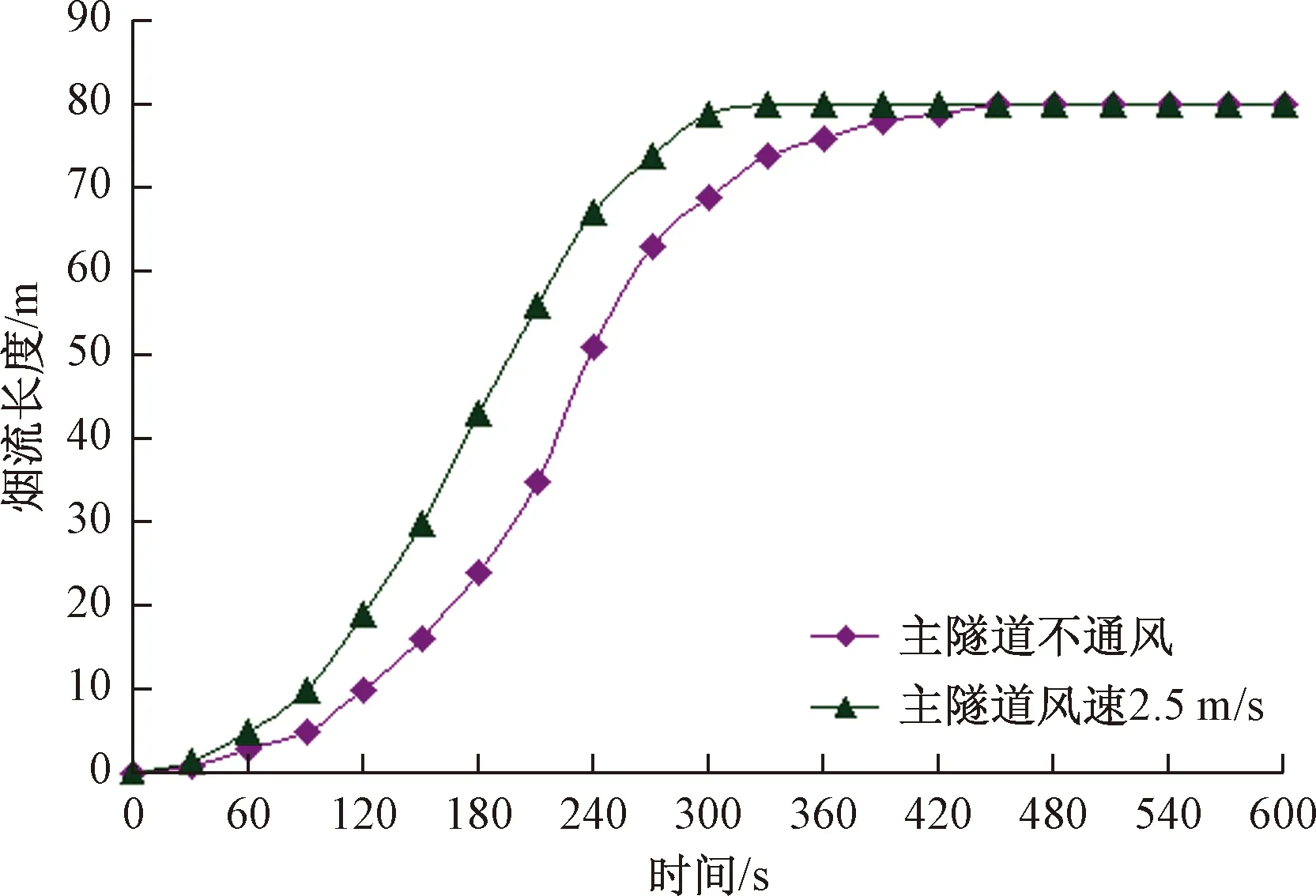
图18 不同主隧道风速下的斜井内烟流长度曲线

由图18可知，与主隧道内不通风情况相比，主隧道内通风时，火灾烟气更容易侵入斜井。主隧道内不通风时，烟气大约在火灾发生后20 s侵入斜井；主隧道内风速为2.5 m/s时，烟气大约在火灾发生后15 s进入斜井。

3 模型试验与数值模拟结果对比分析

采用火灾动力学模拟软件FDS，建立与试验模型参数相同的隧道计算模型，见图19、图20。图20中，绿点代表拱顶温度测点。

图19 计算模型

图20 主隧道内部模型

主隧道内不通风、斜井不同风速(不通风、1 m/s、2 m/s、3 m/s)时，主隧道内拱顶温度的试验及数值计算结果对比见图21。

图21 主隧道内拱顶温度曲线对比

由图21可知，当斜井不通风时，主隧道拱顶最高温度数值模拟结果为710 ℃；当斜井通风风速为1 m/s时，主隧道拱顶最高温度数值模拟结果为650 ℃；当斜井通风风速为2 m/s时，主隧道拱顶最高温度数值模拟结果为580 ℃；当斜井通风风速为3 m/s时，主隧道拱顶最高温度数值模拟结果为550 ℃。拱顶最高温度数值模拟结果随斜井通风速度的增大而降低，与试验结果一致。数值模拟的主隧道拱顶最高温度高于模型试验结果，主要由于隧道模型的制作主材为钢材，燃烧时热量损失较实际情况多，但二者变化规律基本一致。

4 结论

通过对含斜井特长铁路隧道火灾模型试验的研究，得到如下结论：

(1)随着火灾规模的增加，火源上方拱顶最高温度将增大。火灾规模为20 MW和15 MW时，主隧道拱顶最高温度分别为580 ℃和450 ℃。

(2)主隧道内通风工况的拱顶温度低于不通风工况。主隧道内不通风和通风风速2.5 m/s时，拱顶最高温度分别为580 ℃和440 ℃。

(3)斜井向主隧道内送风的风速越大，带有斜井主隧道段内的拱顶温度越低，斜井送风风速为3 m/s时火源拱顶最高温度比不送风时降低80 ℃，斜井送风风速对不带有斜井的主隧道段温度影响较小。

(4)烟气在斜井内的蔓延长度随斜井送风风速的增加而减小。与不送风时相比，送风风速为1 m/s时斜井内烟气长度减少74 m。

(5)确保火灾烟气不进入斜井式紧急出口的临界风速为2 m/s。