导弹打击海上目标中的无源侦察精度影响分析
张怡霄,郭文普,康 凯,姚云龙,张林科,鞠照群
(1.火箭军工程大学 302教研室, 西安 710025; 2.中国人民解放军96816部队, 浙江 金华 322100;3.中国人民解放军96901部队, 北京 100080)
提升弹道导弹打击海面移动目标的能力是当前的发展重点。准确获取海上移动目标的辐射源信息并实现跟踪定位是使用弹道导弹对其成功实施打击的前提[1]。当前天基侦察手段是获取海面移动目标信息的主要来源,但有局限性:一是卫星重访周期较长,获取情报不连续,影响作战时机;二是卫星过顶时间可预测,易被干扰、攻击或是规避[2-3]。
地基无源侦察无上述局限,且有以下优点:收集信息全面,有全天候持续侦察能力,能全面收集敌雷达辐射源参数;探测距离远、覆盖空域宽,能快速实现目标定位;被动侦察消耗功率小,且无暴露阵地风险[4]。
因此,建立地基无源侦察支援下的导弹打击海面移动目标命中概率计算模型,分析地基无源侦察信息精度对导弹命中概率的影响,对提升弹道导弹打击海面移动目标能力具有重要意义。
1 导弹命中海上移动目标概率模型
1.1 导弹命中概率分析
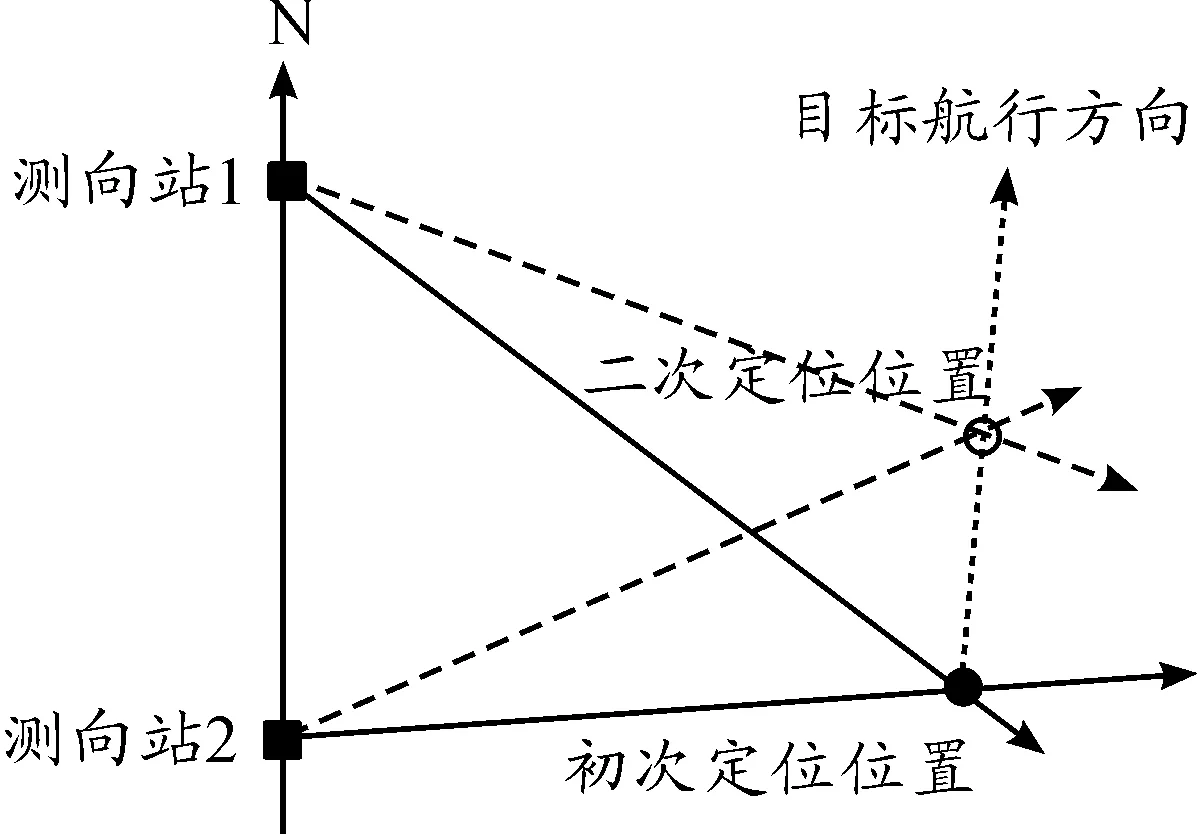
地基无源侦察信息支援弹道导弹打击海面移动目标的具体过程如图 1所示[5-6]。分析该过程可知,一发导弹能够命中目标是以下几个事件构成的共现事件:导弹全飞行过程中各分系统稳定工作;导弹末制导雷达捕获移动目标;导弹自动跟踪目标直至命中。
由概率乘法定理可知,发射一发导弹命中目标概率PHit等于上述各事件概率乘积,即
PHit=PRelia×PCapture×PLead
(1)
其中,PRelia为导弹全飞行过程中各分系统稳定工作的概率,是导弹固有性能指标,与侦察信息精度无关。PLead为导弹自动跟踪目标直至命中概率,对于不同精度的侦察信息变化极小。为便于分析,本文假设导弹系统工作可靠并且无目标对抗,即PRelia=1,导弹自导命中概率PLead为常量[7-8]。
PCapture为导弹末制导雷达成功捕获海上移动目标的概率,与侦察信息精度直接相关。
1.2 导弹末制导雷达捕获概率模型
导弹末制导雷达成功捕获目标需满足两个条件:末制导雷达搜索区能够覆盖目标位置;末制导雷达能够截获并识别目标辐射源信号[9]。
因此,PCapture应为导弹末制导雷达搜索区覆盖目标位置概率PCover,与在搜索区内导弹末制导雷达发现并识别目标概率PIntercept之积,即
PCapture=PIntercept×PCover
(2)
1.3 在搜索区内末制导雷达识别目标概率分析
影响在搜索区内导弹末制导雷达发现并识别目标信号概率PIntercept的因素主要有地基无源侦察提供的目标特征精度,弹载雷达信号处理能力,以及敌方施放干扰影响和电磁环境影响[10]。
由于各弹载雷达信号处理能力不同,敌方干扰影响无法预知,地基无源侦察信息精度对PIntercept的影响无法定量定算[11]。为进一步分析,假设末制导雷达能准确截获搜索区内目标信号,即PIntercept=1。
1.4 末制导雷达搜索区覆盖目标概率模型
导弹末制导雷达的覆盖区域在搜索海上移动目标过程中可简化为平面[12],如图2。
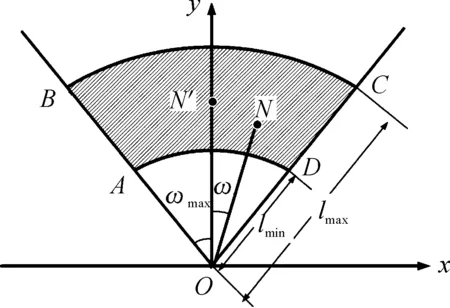
图2 末制导雷达周期内覆盖区域示意图
末制导雷达搜索周期很短,导弹在一个周期内的位移可忽略。因此末制导雷达在一个搜索周期内的覆盖区域可近似为一扇形带状区域,如图2中ABCD所示。其中,O为末制导雷达开机位置,也是导弹自控终点,N是末制导雷达开机时目标实际位置,N′为末制导雷达开机时预测目标位置,L=ON′为末制导雷达开机距离,ωmax为导弹末制导雷达搜索扇面半角,lmax和lmin分别为末制导雷达最大作用距离和最小作用距离,l为末制导雷达开机时目标与导弹的距离,ω为目标方位角。
当目标落在区域ABCD内,认为导弹末制导雷达搜索区覆盖目标,即满足以下条件:
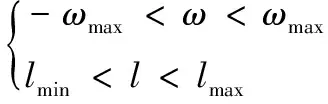
(3)
因此,末制导雷达搜索区覆盖目标概率为
PCover=P{-ωmax<ω<ωmax,lmin (4) 可知,影响末制导雷达搜索区覆盖目标概率PCover的主要因素是目标与末制导雷达的相对位置。地基无源侦察信息的精度直接影响目标与导弹自控终点的相对位置,从而影响覆盖概率。 当前的无源侦察定位常用的定位体制包括测向交叉定位、时差定位、频差定位等。其中测向交叉定位体制的应用最为广泛,技术成熟[12-13]。因此,本文以2站测向交叉定位体制为例进行说明,依据测向交叉的基本原理开展分析。地球曲率、多径效应等客观因素的影响非本文研究重点,暂不考虑。 双站测向交叉定位的基本原理是使用两个测向站对同一目标进行测向,依据三角公式计算得到目标所处位置[14-15]。 如图3所示,设测向站坐标位置分别为P1(x1,y1) 与P2(x2,y2),测得的目标示向角分别为θ1和θ2,则示向线的交点T为目标位置T(xt,yt)。 图3 测向交叉定位示意图 (5) 引起测向误差 Δθ的因素既有固定因素造成的固定系统误差,又有不确定因素造成的随机误差。根据中心极限定理,随机误差一般服从正态分布[18]。因此,本文假设测向站对目标的测向误差 Δθ服从正态分布,即 Δθ~N(μΔθ,σΔθ)。 无源侦察为被动侦察手段,无法直接获取目标的航向和航速信息。当目标保持匀速直线运动时,可以通过相隔一段时间的两次定位结果计算得到目标的航向和航速信息[20]。如图 4所示,设在t1时刻测得目标位置为T1(xt1,yt1),在t2(t2>t1) 时刻,测得目标位置为T2(xt2,yt2),则目标的航行速度vt和航行示向角θt的计算方程分别为 (xt1-xt2)/(yt1-yt2)=-tanθt (xt1-xt2)2+(yt1-yt2)2=[vt(t2-t1)]2 (6) 则由几何关系推导得,航行示向角测量误差 Δθt和航行速度测量误差 Δvt为 (7) (8) 图4 航速及航向计算模型示意图 为了分析无源侦察定位信息与目标相对位置的关系,首先建立末制导雷达覆盖目标坐标系,以导弹自控终点在水平面的投影O为坐标原点,以正北方向为y轴正向,垂直于y轴的正东方向为x轴正向,如图5所示。 图5 目标相对位置与无源侦察信息精度关系 其中M′为最后传递至导弹的测得目标位置,N′为末制导雷达开机时预测的目标位置。则L为导弹预设的末制导雷达开机距离,为固定值。φ为导弹末制导雷达开机时预测目标位置的方位角,服从均匀分布φ~U(0,360)。 可得N′点的坐标(xn′,yn′) 的计算公式为 xn′=L×sinφ,yn′=L×cosφ (9) 设地基无源侦察站利用式测得的目标的航行速度为vt、航行示向角为θt,从最后传递定位信息到导弹末制导开机经过时间为t,则有预测目标航行距离M′N′ 长度为vtt,目标实际航行距离MN长度为(vt-Δvt)t。 可得M′坐标(xm′,ym′) 的计算公式为 xm′=xn′-vtt×sinθt ym′=yn′-vtt×cosθt (10) M为地基无源侦察最后传递定位信息时目标实际位置,设其坐标为(xm,ym) ;则xm=xm′-Δx,ym=ym′-Δy, Δx和 Δy为目标定位误差。 做辅助线使MM′N′C为平行四边形,则目标实际航行方向示向角为α=θt-Δθt。。 通过几何关系推导得,导弹末制导雷达开机时,目标真实位置坐标(xn,yn) 可表示为 (11) 则在导弹末制导雷达开机时,目标真实位置与导弹的距离为 (12) 导弹末制导雷达开机时目标相对导弹位置的方位角为 (13) 设定两个测向站与目标相对位置如图6所示。两测向站连线方向为正北方向,站间距离200 km,在计算目标航向、航速过程中,初次定位与最终定位间隔30 min,且最终定位的目标位置信息即为侦察站最后传递至导弹的目标位置信息。 图6 测向站与目标相对位置示意图 最后传递目标位置至导弹末制导雷达开机共经过30 min,导弹末制导雷达开机时与预测目标距离L为20 km,末端雷达的最大覆盖距离lmax为36 km,最小覆盖距离lmin为4 km,搜索扇面半角ωmax=30°。 导弹全飞行过程中各分系统稳定工作的概率PRelia=1,导弹自动跟踪目标直至命中概率PLead=0.95,在搜索区内导弹末制导雷达发现并识别目标信号概率PIntercept=1。 本文采用蒙特卡洛仿真方法[21]统计得出地面无源侦察信息精度影响下的导弹命中概率。 仿真1:目标距离对导弹命中概率的影响 设目标的真实移动速度为54 km/h,实际航行方向示向角为 30°。初次定位时海上目标相对于测向站1的方位角为 150°,两个测向站的测向误差Δθ1Δθ2均服从μΔθ=0° 的高斯分布。在σΔθ分别取 0.1°、 0.5°、 1°、 2° 的条件下,目标与测向站1的距离与导弹命中概率的对应关系如图7所示。 图7 目标距离对导弹命中概率的影响 由仿真结果可知:随着目标距离增加,命中概率有一定的稳定区间,在区间内距离的增加对命中概率的影响不明显。距离超出稳定区间时,命中概率随着目标距离增加快速下降。测向精度越高,距离稳定区间越大。 仿真2:测向误差对导弹命中概率的影响 设初次定位时海上目标相对于测向站1的方位角为 150°,两个测向站的测向误差 Δθ1Δθ2均服从μΔθ=0° 的高斯分布。在目标航速取20 km/h,目标与测向站1的距离分别为500 km、750 km、1 000 km、1 250 km的条件下,测向站的测向误差标准差σΔθ与导弹命中概率的对应关系如图8所示。 图8 测向误差对导弹命中概率的影响 由仿真结果可知,当目标距离小于500 km时,测向误差的变化对命中概率的影响不明显。当目标距离较远,如大于750 km时,命中概率随着测向误差增加而快速下降。 综合以上仿真结果得到结论:在导弹性能和末制导雷达性能已知的情况下,命中概率对测向误差有一定范围的可接受区间。在可接受区间内,测向精度对导弹命中概率的影响可以忽略,在可接受区间外,导弹命中概率随着测向误差的增加而快速下降。可接受区间的范围与目标距离直接相关,目标距离越远,则对测向误差的可接受区间越小。 同理,当侦察站测向精度已知时,可推算出其对海上移动目标的有效定位距离。在有效定位距离内,测向精度的变化对命中概率影响不明显。如果超出有效定位距离,即使测向误差波动很小,也会造成命中概率的剧烈变化。 本文以无源侦察定位中常用的测向交叉定位体制为例,建立了地基无源侦察定位支援下的导弹命中概率计算模型。该模型可以为地基无源侦察力量的建设规划、装备发展提供依据,对提升导弹打击海上目标的能力有较大意义。通过蒙特卡洛方法仿真分析了测向精度对导弹命中概率的影响。仿真结果表明:在可接受区间内,测向精度对命中概率的影响可以忽略,在可接受区间外,命中概率随着测向精度的降低而快速下降。可接受区间的范围与目标距离直接相关,目标距离越远,则对测向误差的可接受区间越小。需要注意的是,本文建立的命中概率计算模型和仿真分析是基于一般测向交叉定位原理和匀速直线运动的目标建立的,在指导实际应用时有一定局限性。2 无源侦察精度影响模型
2.1 双站测向交叉定位精度分析
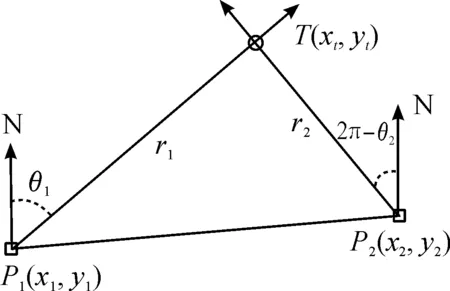
2.2 目标航速及航向计算模型及精度分析
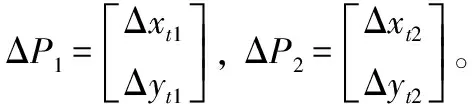
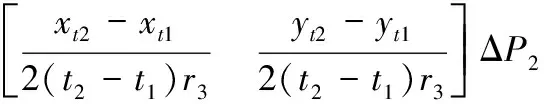
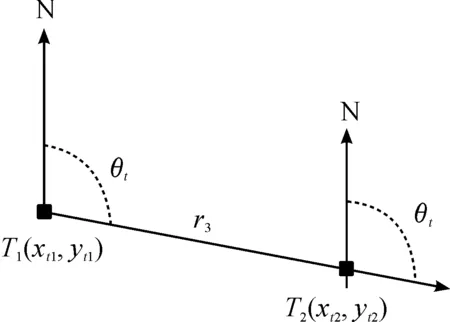
2.3 地基无源侦察信息精度影响模型


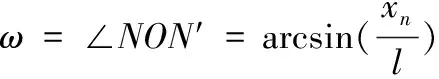
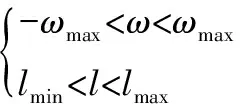
3 蒙特卡洛仿真分析
4 结论

