α Decay Properties of Even-Even Nuclei 296−308120 Within the Two-Potential Approach∗
Jun-Yao Xu (徐俊瑶), Jiu-Long Chen (陈玖龙), Jun-Gang Deng (邓军刚), Jun-Hao Cheng (程俊皓), Hong-Ming Liu (刘宏铭), and Xiao-Hua Li (李小华),2,3
1School of Nuclear Science and Technology, University of South China, Hengyang 421001, China
2Cooperative Innovation Center for Nuclear Fuel Cycle Technology & Equipment, University of South China, Hengyang 421001, China
3Key Laboratory of Low Dimensional Quantum Structures and Quantum Control, Hunan Normal University, Changsha 410081, China
Abstract In the present work, we predict the α decay half-lives of unknown even-even nuclei 296−308120 within the two-potential approach, whose α decay energy Qα is calculated using WS3+ mass model.To reduce the deviations between the predictions and experimental data due to nuclear shell effect, the analytic formula of α decay hindrance factor is introduced to the two-potential approach, whose parameters had been extracted from even-even nuclei in the region of 82 < Z ≤126 and 152 < N ≤184 in our previous work [Deng et al., Chin.Phys.C 42 (2018) 044102].In addition, for comparing, we use a type of α decay general formula Universal Decay Law (UDL) and a semi-empirical formula in the superheavy nucleus (SEMFLS) to calculate the half-lives of even-even nuclei 296−308120.The results indicate that our predicted values and the calculated values of the above two empirical formulas are mutually confirmed.Meanwhile, we systematically study α decay chains of 296−308120 and predict the decay modes for superheavy nuclei to help to identify new superheavy isotopes.
Key words: α decay, two-potential approach, even-even nuclei with Z=120, hindrance factor
1 Introduction
The synthesis of heavy elements are of great significance to expand the periodic table of elements and prove the existence about the island of the stable superheavy element.However, the synthesis of superheavy elements and superheavy nuclei containing more neutrons is facing many challenges.It requires that closely combining theory and experiment, and exploring the properties and synthetic mechanism of superheavy nuclei to board the island of the stable superheavy element.[1]In recent years,through hot-fusion reactions between48Ca beams and radioactive actinide targets, element 118 had been successfully synthesized.[2]In the future,if the nucleus ofZ=120 is successfully synthesized, it will be the nucleus with the largest number of protons and neutrons, and be closest to the predictedN=184 shell closure, which will promote the development of heavy ion physics[1]and help to prove the existence of the island of the stable superheavy element.
Spontaneous fission andαdecay are the two main decay modes of superheavy nuclei.For the most of the synthesized proton-rich superheavy nuclei,αdecay is more dominant than spontaneous fission.[3]Recent works[4−6]shown that the decay modes of even-even nuclei296−308120 wereαdecay.Through studyingαdecay, we can obtain some important information about nuclear shell structure such as ground state properties,energy level structure and so on.[7]
Up to now, there are many theoretical models and formulas have been used to describe the process ofαdecay such as the cluster model,[8−10]the liquid drop model,[11−15]the unified model forαdecay andαcapture,[16−17]the empirical formulas,[18−22]the ImSahu formula,[23]the effective liquid drop model (ELDM),[24]the Xu formula[25]and so on.Recently, the two-potential approach (TPA), which can obtain a simple algebraic formula for theαdecay width,[26]has been widely used to calculate the half-life ofαdecay.[27−34]In our previous works,[30−38]we systematically studied theαdecay halflives andαdecay preformation probabilities or hindrance factor of heavy nuclei and superheavy nuclei.Meanwhile,we also predicted theαdecay half-lives of superheavy nuclei within the two-potential approach.Our calculations and predictions can well conform to the experimental data.
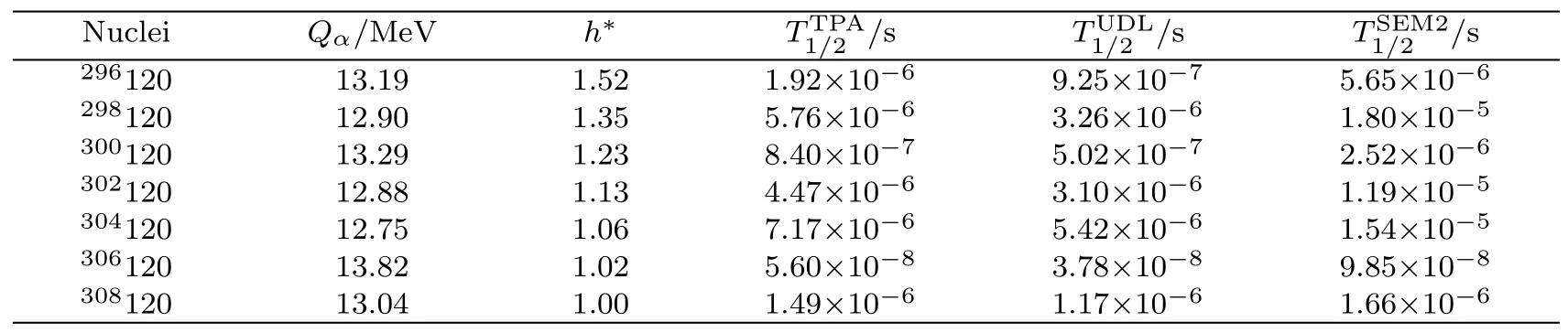
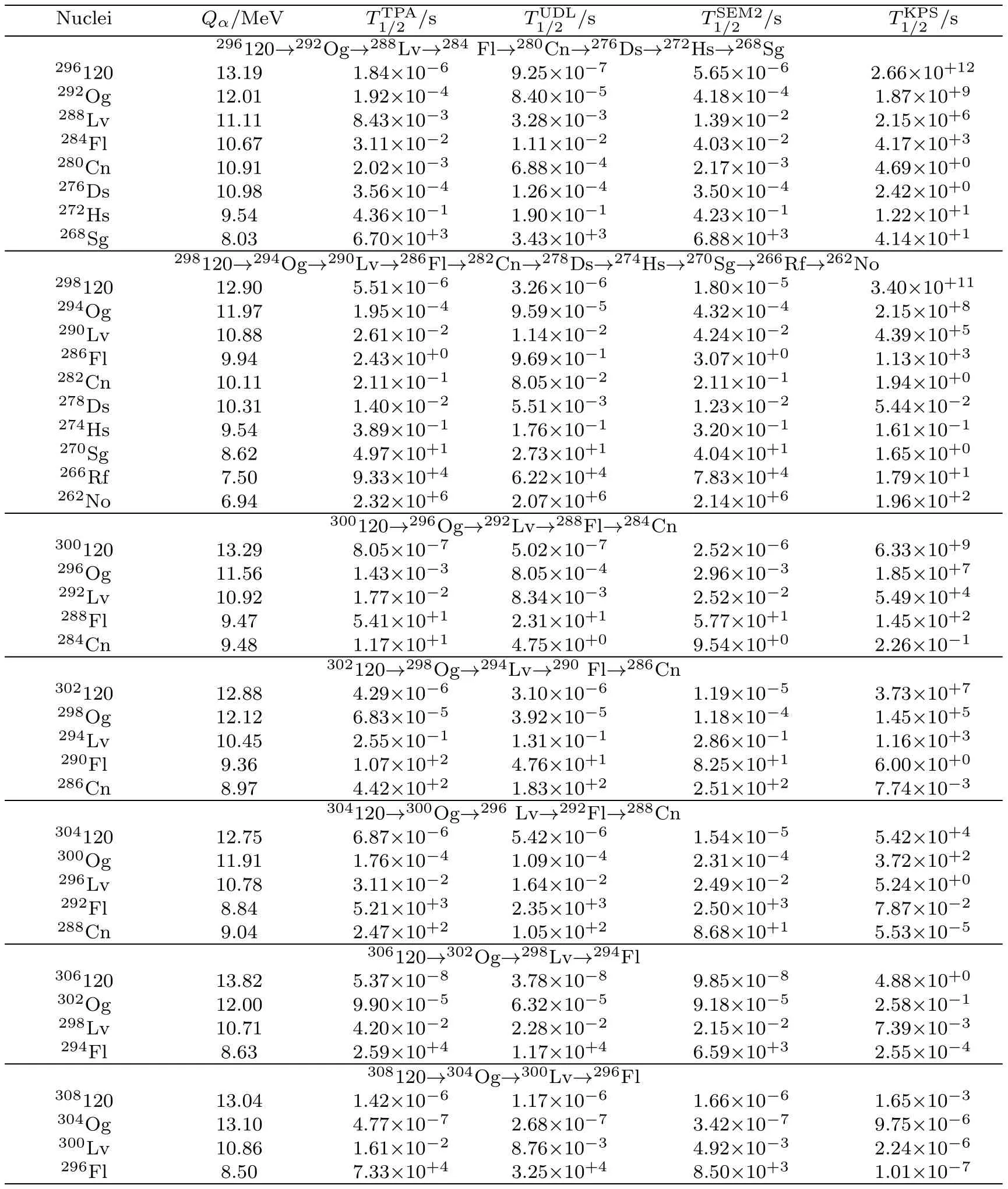
In this work,for providing theoretical reference for experiment synthesizing the even-even nuclei296−308120,we predictαdecay half-lives of these nuclei.Because theαdecay half-life is sensitive toαdecay energyQα, how to calculateQαof unknown nuclei becomes a key question.Recently, Sobiczewski[39]analyzedαdecay energyQαusing nine different mass models as follow Mölleret al.(FRDM)[40]Duflo and Zuker (DZ),[41]Nayak and Satpathy (INM),[42]Wang and Liu (WS3+),[43]Wanget al.(WS4+),[45−46]and Muntianet al.(HN),[47−48]Kuzminaet al.(TCSM),[49]Gorielyet al.(HFB31),[50]and Liranet al.(SE).[51]It was found that the deviation between theQαcalculated by WS3+ and the experimental data is the minimal.Therefore in this work we use the WS3+ mass model to calculate theαdecay energyQαof even-even nuclei296−308120.To reduce the deviations between the predictions and experimental data due to the nuclear shell structure,the analytic formula ofαdecay hindrance factor is introduced to the two-potential approach,whose parameters are given in our previous work extracted from eveneven nuclei in region of 82 Because many new superheavy isotopes were identified by theαdecay chain.For helping the future experimental synthesis more effectively, it is significant to predict theαdecay and spontaneous fission half-lives along theαdecay chain.Recently, there are many models had been used to describe the process of spontaneous fission such as the generalized Swiatecki’s formula,[54−56]the Santhosh(KPS) formula,[57]the Karpov (AVK) formula,[58]and so on.Compared to AVK formula without isospin effect,Zhaoet al.[44]find that the isospin effect contributions are considered in the analytical formula (KPS formula),the theoretical results can better reproduce the experimental spontaneous fission half-lives.In this work, we calculat theαdecay half-lives along296−308120 of theαdecay chain by TPA, UDL, SEMFLS2.While the calculations of spontaneous fission half-lives are carried out by KPS formula. This article is organized as follows.In the next section,theoretical framework for calculatingαdecay half-life is briefly described.The detailed calculations and discussion are presented in Sec.3.Finally, a summary is given in Sec.4. In the framework of the TPA, the expression of theαdecay half-life is as follows whereµ=mdmα/(md+mα) is the reduced mass of the daughter nucleus andαparticle, withmdandmαbeing the mass of the daughter nucleus andαparticle, respectively.In accordance with the calculations by adopting the density-dependent cluster model (DDCM),[59]theαpreformation factorP0is 0.43 for even-even nuclei. his the hindrance factor denoting the deviation between the experimentalαdecay half-life and calculation,which can be written as where,represent experimental and calculated values.Recently,a simple formula for estimating the variation in theαdecay hindrance factor,which considers the nuclear shell effect and proton-neutron interaction, was put forward[30,60−61]and written as wherea,b,c,dandeare adjustable parameters.Z,NandAare the proton number, neutron number and mass number of the parent nucleus, respectively.Z1,Z2andN1,N2denotes proton and neutron magic numbers withZ1 The normalized factorFis given by internal integration, which can be written as wherek(r)=is the wave number ofαparticle withrbeing the mass center distance between theαparticle and the daughter nucleus. P, the semiclassical Wentzel-Kramers-Brillouin (WK B) barrier penetration probability, can be calculated by wherer1,r2andr3(Eq.(5)) are the classical turning points, which can be obtained by through equationsV(r1)=V(r2)=V(r3)=Qα. Theα-core potentialV(r)is composed of the Coulomb potentialVC(r),nuclear potentialVN(r)and the centrifugal potentialVl(r), which is expressed as The Coulomb potentialVC(r)is taken as the potential of a uniformly charged sphere with sharp radiusR, which is expressed as follows whereZdandZαare the proton numbers of daughter nucleus and theαparticle, respectively.In this work,we choose a type of cosh parametrized form forVN(r),obtained by analyzing experimental data ofαdecay,[62]which is written as where the nuclear potential depthV0=192.42 +31.059[(Nd −Zd)/Ad]MeV withNd,ZdandAdbeing denoted the number of neutron,proton and mass of daughter nucleus, respectively.The nuclear potential diffusenessa0=0.5958 fm.Ris calculated by the nuclear droplet model and proximity energy, and expressed as Becausel(l+1)→(l+1/2)2is a necessary correction for one-dimensional problems,[63]in this work we adopt the Langer modified centrifugal barrierVl(r), which can be expressed as whereldenotes the orbital angular momentum taken away by theαparticle.l=0 for the even-even nucleiαdecays. From Sec.2, we can know thatαdecay energy and the hindrance factors are important inputs for calculatingαdecay half-life.Based on the conclusion of Ref.[39],we use the WS3+ mass model to calculate theαdecay energy.In our previous works,[36]theαdecay energy for the nuclei from250Cm to294Og were also calculated by WS3+.The calculations can reproduce the experimental data well. In our previous works,[30,32−33,37]the two-potential approach (TPA)[26,64]was used to systematically study theαdecay hindrance factors and/or preformation probabilities for even-even, odd-A and doubly-odd nuclei.It is found that the behaviors of theαdecay hindrance factors and/or preformation probabilities of the same kinds of nuclei (even-even nuclei, odd-A nuclei and doubly-odd nuclei) in the same region are similar, while the regions are divided by the magic numbers of proton and neutron.Meanwhile, theαdecay half-lives of 20 even-even nuclei in region of 82< Z ≤126 and 152< N ≤184(from250Cm to294Og)[36]were systematically calculated by adopting the TPA in Ref.[36].The correspondingαdecay hindrance factors as well as a new set of parameters of hindrance factors considering the nuclear shell effect were extracted.The standard deviations ofαdecay halflives between predictions considering the hindrance factor correction and experimental data for these 20 even-even nuclei, which is from 0.32 to 0.26 when the new parameters are used.For comparing to TPA with unconsidering theαhindrance factors, our model obviously improved by (0.32−0.26)/0.32=18.75%.To clearly observe the reduction of standard deviation, which is considering the hindrance factors, we plot the decimal logarithm deviations between the experimental data of 20 even-even nucleiαdecay half-lives and calculations in Fig.1.In this figure, it obviously indicates that the half-lives calculated by the TPA with consideringαdecay hindrance factors are better than the ones unconsidering. Fig.1 (Color online) Decimal logarithm deviations between the experimental data of α decay half-lives and calculations.The circles and diamonds refer to results obtained by the TPA with the hindrance factors being considered and unconsidered, denoted as Calc1 and Calc2,respectively. Table 1 The parameters of α decay hindrance factor for even-even nuclei from 82 These phenomena motivate our interest to further predict the half-lives of superheavy nuclei.The aim of this work is to predict theαdecay half-lives of unknown eveneven nuclei with296−308120 within the two-potential approach, whoseαdecay energyQαare calculated using WS3+ mass model.To reduce the deviations of the predictions due to the nuclear shell effect,the analytic expression of hindrance factorsh∗is employed, whose parameters had been extracted from Ref.[36].The calculations ofQα,h∗which are obtained by Eq.(4) andare shown in column 2, 3 and 4 of Table 2, respectively. For comparatively, we use aαdecay general formula Universal Decay Law (UDL), which the agreement between experiment and the UDL is excellent,[53]and a semiempirical formula in the superheavy nucleus (SEMFLS2).Wanget al.[52]compared 18 different models and found that the half-life calculated by SEMFLS2 model has the smallest deviation from the experimental value.The halflives of nuclei with296−308120 calculated using UDL and SEMFLS2 are shown in column 5 and 6 of Table 2.From this table,we can see thatαdecay half-lives calculated by three models agree well with each other. In order to compare the calculated results of the three methods with a more intuitive view, we take the logarithmic form of the calculation results, as shown in Fig.2.From this figure,we can clearly observe that the half-lives calculated by the TPA is well in between the values calculated by the other two methods. Fig.2 (Color online) The three theoretical methods are used to calculate the Logarithmic half-lives data of even-even nuclei with Z=120 and its isotopes.The blue triangle,black square and red dot represent the T1/2 predicted by the SEMFLS2 TPA and UDL, respectively. Fig.3 (Color online)Comparison of the calculated α decay half-lives with the corresponding spontaneous fission(SF) half-lives of the isotopes 296−308120 and products on its α decay chain. Table 2 The calculated results of T1/2 for Z=120, N=176, 178,..., 188 by TPA, UDL, and SEMFLS2.Meanwhile, from WS3+.[43] Table 2 The calculated results of T1/2 for Z=120, N=176, 178,..., 188 by TPA, UDL, and SEMFLS2.Meanwhile, from WS3+.[43] Nuclei Qα/MeV h∗TTPA 1/2 /s TUDL 1/2 /s TSEM2 1/2 /s 296120 13.19 1.52 1.92×10−6 9.25×10−7 5.65×10−6298120 12.90 1.35 5.76×10−6 3.26×10−6 1.80×10−5300120 13.29 1.23 8.40×10−7 5.02×10−7 2.52×10−6302120 12.88 1.13 4.47×10−6 3.10×10−6 1.19×10−5304120 12.75 1.06 7.17×10−6 5.42×10−6 1.54×10−5306120 13.82 1.02 5.60×10−8 3.78×10−8 9.85×10−8308120 13.04 1.00 1.49×10−6 1.17×10−6 1.66×10−6 Table 3 The calculated results of α decay chain of 296−308120 by TPA, UDL, SEMFLS2 and KPS.Meanwhile, from WS3+.[31] Table 3 The calculated results of α decay chain of 296−308120 by TPA, UDL, SEMFLS2 and KPS.Meanwhile, from WS3+.[31] Nuclei Qα/MeV TTPA 1/2 /s TUDL 1/2 /s TSEM2 1/2 /s TKPS 1/2 /s 296120→292Og→288Lv→284 Fl→280Cn→276Ds→272Hs→268Sg 296120 13.19 1.84×10−6 9.25×10−7 5.65×10−6 2.66×10+12292Og 12.01 1.92×10−4 8.40×10−5 4.18×10−4 1.87×10+9288Lv 11.11 8.43×10−3 3.28×10−3 1.39×10−2 2.15×10+6284Fl 10.67 3.11×10−2 1.11×10−2 4.03×10−2 4.17×10+3280Cn 10.91 2.02×10−3 6.88×10−4 2.17×10−3 4.69×10+0276Ds 10.98 3.56×10−4 1.26×10−4 3.50×10−4 2.42×10+0272Hs 9.54 4.36×10−1 1.90×10−1 4.23×10−1 1.22×10+1268Sg 8.03 6.70×10+3 3.43×10+3 6.88×10+3 4.14×10+1298120→294Og→290Lv→286Fl→282Cn→278Ds→274Hs→270Sg→266Rf→262No 298120 12.90 5.51×10−6 3.26×10−6 1.80×10−5 3.40×10+11294Og 11.97 1.95×10−4 9.59×10−5 4.32×10−4 2.15×10+8290Lv 10.88 2.61×10−2 1.14×10−2 4.24×10−2 4.39×10+5286Fl 9.94 2.43×10+0 9.69×10−1 3.07×10+0 1.13×10+3282Cn 10.11 2.11×10−1 8.05×10−2 2.11×10−1 1.94×10+0278Ds 10.31 1.40×10−2 5.51×10−3 1.23×10−2 5.44×10−2274Hs 9.54 3.89×10−1 1.76×10−1 3.20×10−1 1.61×10−1270Sg 8.62 4.97×10+1 2.73×10+1 4.04×10+1 1.65×10+0266Rf 7.50 9.33×10+4 6.22×10+4 7.83×10+4 1.79×10+1262No 6.94 2.32×10+6 2.07×10+6 2.14×10+6 1.96×10+2300120→296Og→292Lv→288Fl→284Cn 300120 13.29 8.05×10−7 5.02×10−7 2.52×10−6 6.33×10+9296Og 11.56 1.43×10−3 8.05×10−4 2.96×10−3 1.85×10+7292Lv 10.92 1.77×10−2 8.34×10−3 2.52×10−2 5.49×10+4288Fl 9.47 5.41×10+1 2.31×10+1 5.77×10+1 1.45×10+2284Cn 9.48 1.17×10+1 4.75×10+0 9.54×10+0 2.26×10−1302120→298Og→294Lv→290 Fl→286Cn 302120 12.88 4.29×10−6 3.10×10−6 1.19×10−5 3.73×10+7298Og 12.12 6.83×10−5 3.92×10−5 1.18×10−4 1.45×10+5294Lv 10.45 2.55×10−1 1.31×10−1 2.86×10−1 1.16×10+3290Fl 9.36 1.07×10+2 4.76×10+1 8.25×10+1 6.00×10+0286Cn 8.97 4.42×10+2 1.83×10+2 2.51×10+2 7.74×10−3304120→300Og→296 Lv→292Fl→288Cn 304120 12.75 6.87×10−6 5.42×10−6 1.54×10−5 5.42×10+4300Og 11.91 1.76×10−4 1.09×10−4 2.31×10−4 3.72×10+2296Lv 10.78 3.11×10−2 1.64×10−2 2.49×10−2 5.24×10+0292Fl 8.84 5.21×10+3 2.35×10+3 2.50×10+3 7.87×10−2288Cn 9.04 2.47×10+2 1.05×10+2 8.68×10+1 5.53×10−5306120→302Og→298Lv→294Fl 306120 13.82 5.37×10−8 3.78×10−8 9.85×10−8 4.88×10+0302Og 12.00 9.90×10−5 6.32×10−5 9.18×10−5 2.58×10−1298Lv 10.71 4.20×10−2 2.28×10−2 2.15×10−2 7.39×10−3294Fl 8.63 2.59×10+4 1.17×10+4 6.59×10+3 2.55×10−4308120→304Og→300Lv→296Fl 308120 13.04 1.42×10−6 1.17×10−6 1.66×10−6 1.65×10−3304Og 13.10 4.77×10−7 2.68×10−7 3.42×10−7 9.75×10−6300Lv 10.86 1.61×10−2 8.76×10−3 4.92×10−3 2.24×10−6296Fl 8.50 7.33×10+4 3.25×10+4 8.50×10+3 1.01×10−7 Because many new superheavy isotopes were identified by theαdecay chain of unknown nuclei to known nuclei.In this work, we also systematically studyαdecay chains of296−308120 and predict the decay modes of nuclei on the decay chains.Theαdecay half-lives are calculated by TPA, UDL and SEMFLS2.The calculations of spontaneous fission half-lives are carried out by KPS formula,[44]whose theoretical results can well reproduce the experimental spontaneous fission half-lives.The calculations are listed in columns 3, 4, 5, and 6 of Table 3, respectively.To intuitively know the decay modes of each nuclei, theαhalf-lives and spontaneous fission half-lives of each nuclei along the chain are shown in Fig.3.In this figure, we know the decay modes of each nuclei in theαdecay chains of296−308120 clearly, and the results are agreed well with NUBASE2003[65]and AME2003.[66−67]The calculations are extended to provide some predictions forαdecay and spontaneous fission half-lives, which will be useful for future experiments to synthesize and detect new superheavy nuclei. In summary,we adopt the two-potential approach taking the analytic formula ofαdecay hindrance factors,which is considered the nuclear shell effect and protonneutron interaction and inputαdecay energyQαcalculated by WS3+ mass model to predictαdecay half-lives of unknown even-even nuclei296−308120.In addition, our results are compared with calculations of UDL and SEMFLS2.The three calculations are mutually confirmed.It is indicated that our predicted theαdecay half-lives of nucleus296−308120 are credible.For predicting the decay modes for superheavy nuclei, we compareαhalf-lives and spontaneous fission half-lives.The values are agreed well with experimental result.It will be more helpful for future experiments.2 Theoretical Framework
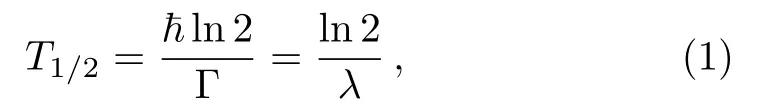



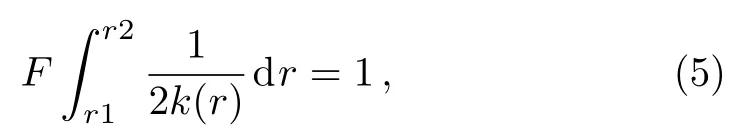

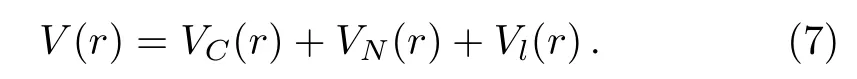
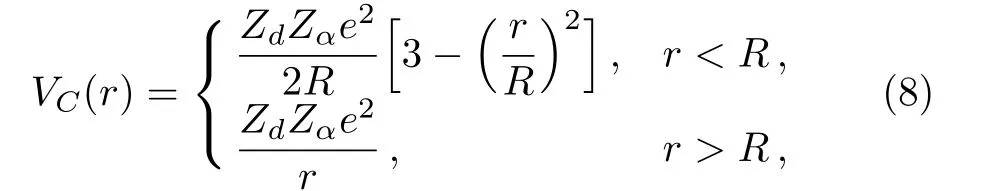

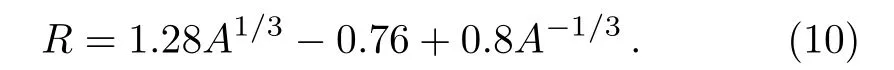

3 Results and Discussion




4 Summary
 Communications in Theoretical Physics2019年11期
Communications in Theoretical Physics2019年11期
