A Gravitational Wave Background from Primordial Black Hole Lattices in Matter Dominated Era∗
Ke Wang (王科)
National Astronomical Observatories,Chinese Academy of Sciences,20A Datun Road,Beijing 100012,China
Abstract We use the wide-used Einstein Toolkit to solve the Einstein constraints and then simulate the expansion of primordial black hole lattices(PBHLs)with different value of fPBH and mPBH.We find that fPBH plays an important role during the evolution of PBHLs.Since the motion of primordial black holes (PBHs) caused by the expansion of PBHLs occurs at speeds close to that of light,we expect the emission of gravitational waves (GWs) during the expansion of PBHLs.We use both analytical estimates and numerical simulations to cross check the production of GWs in expanding PBHLs.
Key words: Einstein Toolkit,primordial black hole lattices,gravitational waves
1 Introduction
Observations of gravitational waves (GWs) by LIGO/VIRGO[1−5]have proved there should be a gravitational wave background (GWB) produced by the black hole and neutron star binaries’ coalescence.Meanwhile,people also believe there is a primordial inflationary GWB from tensor perturbations generated by quantum fluctuations during inflation even though Planck didn’t measure it.[6]Besides that,there are many other theories (or sources)which can produce GWBs,such as reheating after inflation,[7]thermal phase transitions from the decays of cosmic strings.[8]Here we expect that there is a GWB from primordial black hole lattices (PBHLs) in matter dominated era.
During the radiation era,any large enough perturbations can collapse to form Primordial Black Holes(PBHs).[9]To what extend can the configuration of PBHs just after the epoch of matter-radiation equality be considered as a PBHL? As we know,a pair of PBHs would decouple from the expansion of the Universe and form a gravitationally bound system if the average energy density of PBHs over the volumeR3is larger than the total background cosmic energy densityρt,that is,ifmPBHR−3>ρt.Since,we know that most of PBHs are gravitationally free on average in matter dominated era.On the other hand,due to the cosmological principle that the Universe is homogeneous and isotropic on large scales,we can say that the PBHL is the most reasonable configuration of PBHs with a monochromatic mass distribution on our hands.
In fact,there is a cosmological model,black hole lattices (BHLs),[10−13]to investigate the so-called “backreaction” that the local inhomogeneities can affect the global expansion of the Universe.For review of BHLs,see Ref.[14].It is worth pointing out that the PBHLs does not serve as a cosmological model like BHLs does but is an early epoch of the Universe.In practice,however,we do apply the same technologies developed by[11−13]when they evolve the BHLs in numerical relativity to the PHBLs.
Here we will turn to the wide-used Einstein Toolkit[15]to solve the Einstein constraints and simulate the spacetime and hydrodynamical evolution.More precisely:the thorn CT-MultiLevel (and CT-Analytic)[16]gets the initial data of PBHLs; the thorn ML_BSSN[17−19]evolves spacetime using the Baumgarte-Shapiro-Shibata-Nakamura (BSSN) formalism;[20−22]the thorn GRHydro evolves the hydrodynamical system.[23−25]
This paper is organized as follows.In Subsec.2.1,we give the Einstein constraints of PBHLs with dust.In Subsec.2.2,we solve the Einstein constraints of PBHLs with different value offPBHandmPBH.In Subsec.3.1,we show the expansion of PBHLs with different value offPBHandmPBH.In Subsec.3.2,we use both analytical estimates and numerical simulations to derive the production of GWB in PBHLs.At last,a brief summary and discussion are included in Sec.4.
In this paper,we adopt the following conventions:Greek indices run in{0,1,2,3},Latin indices run in{1,2,3}and repeated indices imply summation and we are in a geometric unit system withG=c=M⊙=1.
2 Initial Data of Primordial Black Hole Lattices
To mock an infinite 3-dimensional lattice in our simulations,we impose the periodic boundary conditions on a cubic withxiin [−5,5].A PBH is located at the center of cubic and surrounded by flat-distributed dust with energy densityρm.It is worth noting that our simulation is not done in Schwarzschild coordinates but in its isotropic coordinates.For simplicity,we just add the dust outside the PBH horizonrh=0.5mPBHso that the inner boundary conditions of PBHLs can be set as that of a single puncture.[26]And there are no outer boundary conditions for PBHLs.Although the set up of initial data is usually a non-trivial task,here we can solve PBHLs’ coupled system of one non-linear and three linear elliptic partial differential equations thanks to Refs.[11,13,16]
2.1 Einstein Constraints of Primordial Black Hole Lattices
The initial data of PBHLs must satisfy their Hamiltonian constraint and momentum constraint

where the 3-metricγijis the intrinsic metric,Kijis the extrinsic curvature,Ris 3-Ricci scalar,Diis the covariant derivative associated withγij,Eis the matter energy density,andpiis the matter momentum density as measured by the Eulerian observer.After conformal decomposition ofγijandKijwith the conformal factor Ψ
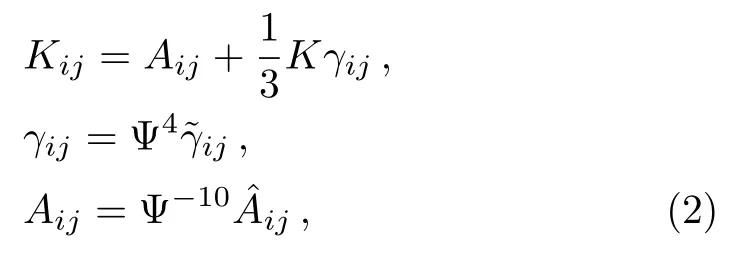
we can get the conformal Einstein constraints

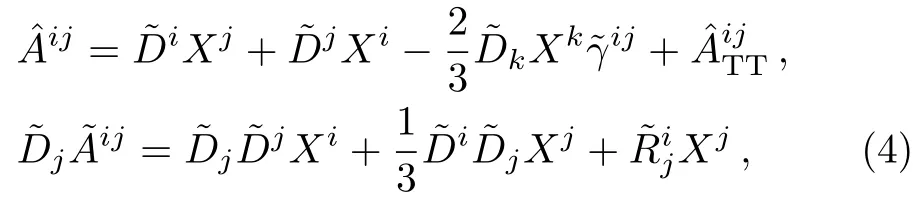
and choosing the free data as the following
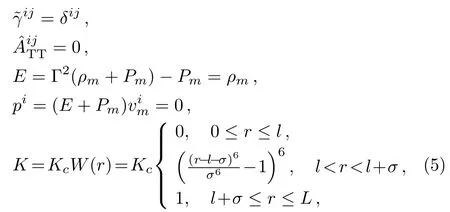
we can get the conformal transverse traceless form of Einstein constraints for PBHLs

where we have expanded the conformal factor as
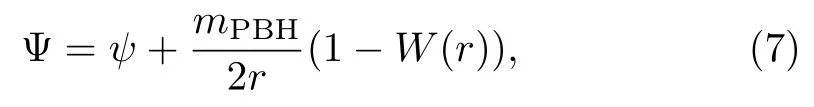
according to the inner boundary conditions of a single puncture.
2.2 Solving the Einstein Constraints
We use a multigrid approach[16]to solving the Einstein constraints(6).But we impose the integrability condition as[11]
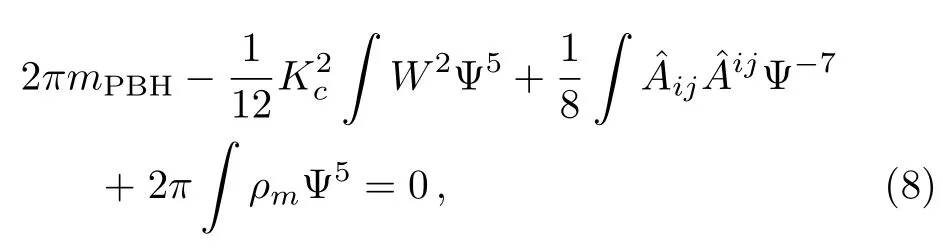
at the end of each relaxation step to determine the negative parameterKc.Finally we perform the inner resetting

at the end of every relaxation step.
Table 1 shows the parameters setting of ten PBHLs and Table 2 shows the solution of the Einstein constraints of ten PBHLs when all of 5 refinement levels cover the whole domain with spacing 1,0.5,0.25,0.125,and 0.0625 respectively.Comparing L0 to L7,L8 and L9,we can see that a smaller PBH massmPBHgives a shorter initial proper cubic edgeDedge(τ=0) and leads a lower initial expansion rate−Kc.Comparing L0 to L4,L5 and L6,we can see that a higher matter energy densityρmhas a higher initial expansion rate−Kcbut produces a shorter initial proper cubic edgeDedge(τ=0).Comparing L0 to L1,L2 and L3,we can see that a larger PBH massmPBHand a smaller matter energy densityρmstill produce a larger initial proper cubic edgeDedge(τ=0) but lead a lower initial expansion rate−Kc.That is to say,the initial expansion rate−Kcis more sensitive to the matter energy densityρmthan the PBH massmPBH.From the Table 2,we can also see that a smaller PBH massmPBHviolates the Hamiltonian constraint more severely.
In Fig.1,the Ψ =ψ >1 at the boundary means that each PBH is gravitationally coupled to its neighbors;the boundaryψof L0 is larger than that of L9 just because the PBH with larger mass will be gravitationally coupled to its neighbors more tightly; the boundaryψof L0 is larger than that of L6,which means the matter surrounding the PBH suppresses the gravitational correlation among PBHs; the boundaryψof L0 is larger than that of L3,which is consistent with above two cases.In Fig.2,we give the solutions ofX1of PBHLs.In Fig.3,we show the initial Hamiltonian constraint violation of PBHLs.
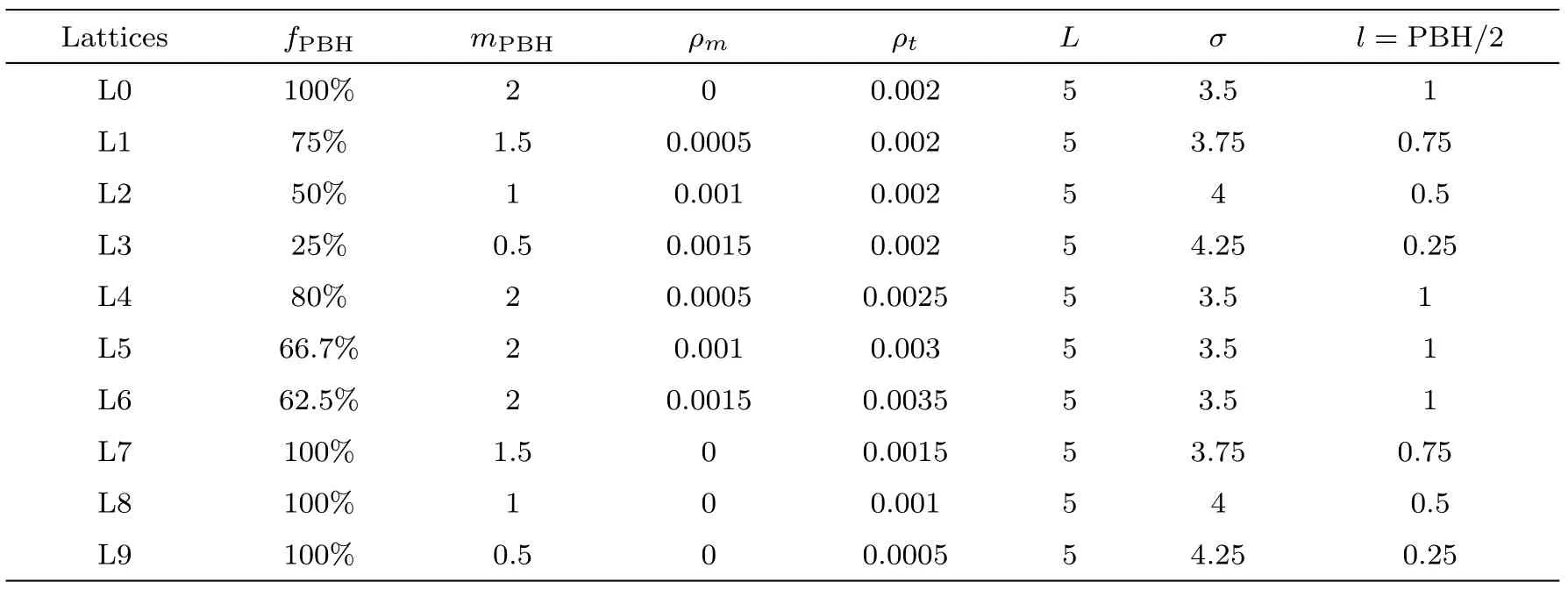
Table 1 The parameters setting of ten PBHLs.
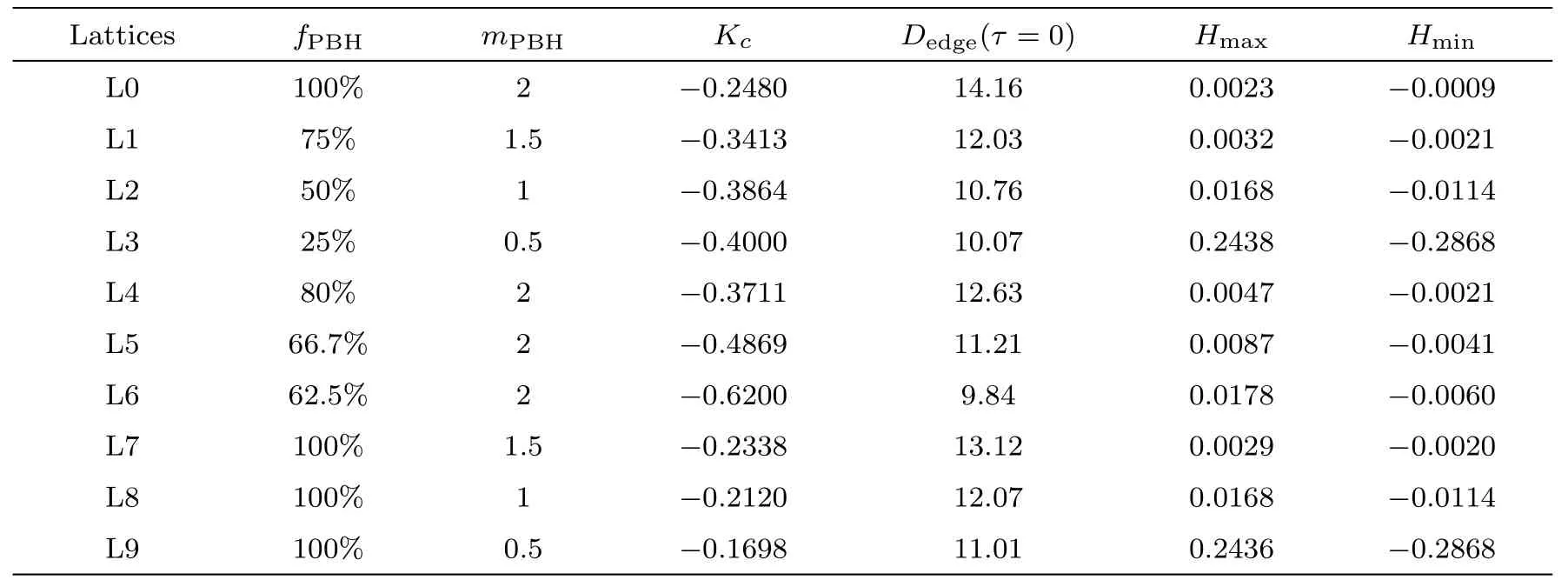
Table 2 The solution of the Einstein constraints of ten PBHLs with spacing of the finest one of 5 refinement levels equal to 0.0625.
The last plot in Figs.1,2,and 3 is a convergence test for solving the initial data and shows theψ,X1andHof L0 with spacing of the finest one of 5 refinement levels equal to 0.0625 (L0f),0.078125 (L0m),and 0.1041667(L0c) respectively.
3 Time Evolution of Primordial Black Hole Lattices
Given the initial data of PBHLs,we can simulate the time evolution of PBHLs.Due to the negative trace of the extrinsic curvatureKijaround the boundary,we can expect an expansion of PBHLs during the time evolution.Meanwhile,since the motion of PBHs caused by the expansion of PBHLs occurs at speeds close to that of light,we also expect the emission of GWs during the time evolution.
3.1 Expansion of Primordial Black Hole Lattices
In order to circumvent the central puncture,here we will study the expansion of PBHLs through the rescaling of the proper length of lattice cells’edge with proper time.The proper time at anywhere is given by integrating the corresponding lapse functionα(t,x)from the beginning of simulation


Fig.1 ψ of PBHLs as a function of position.
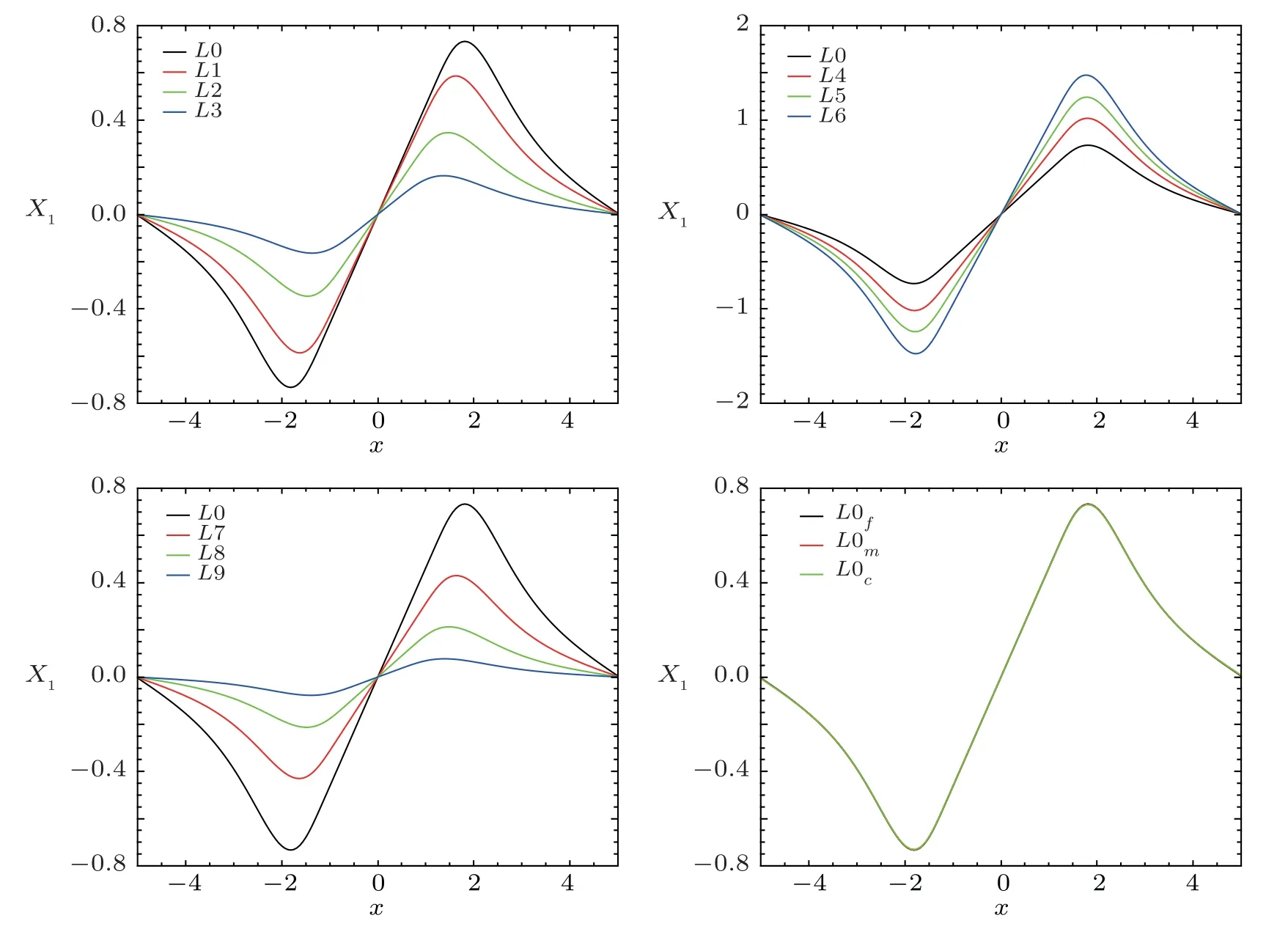
Fig.2 X1 of PBHLs as a function of position.
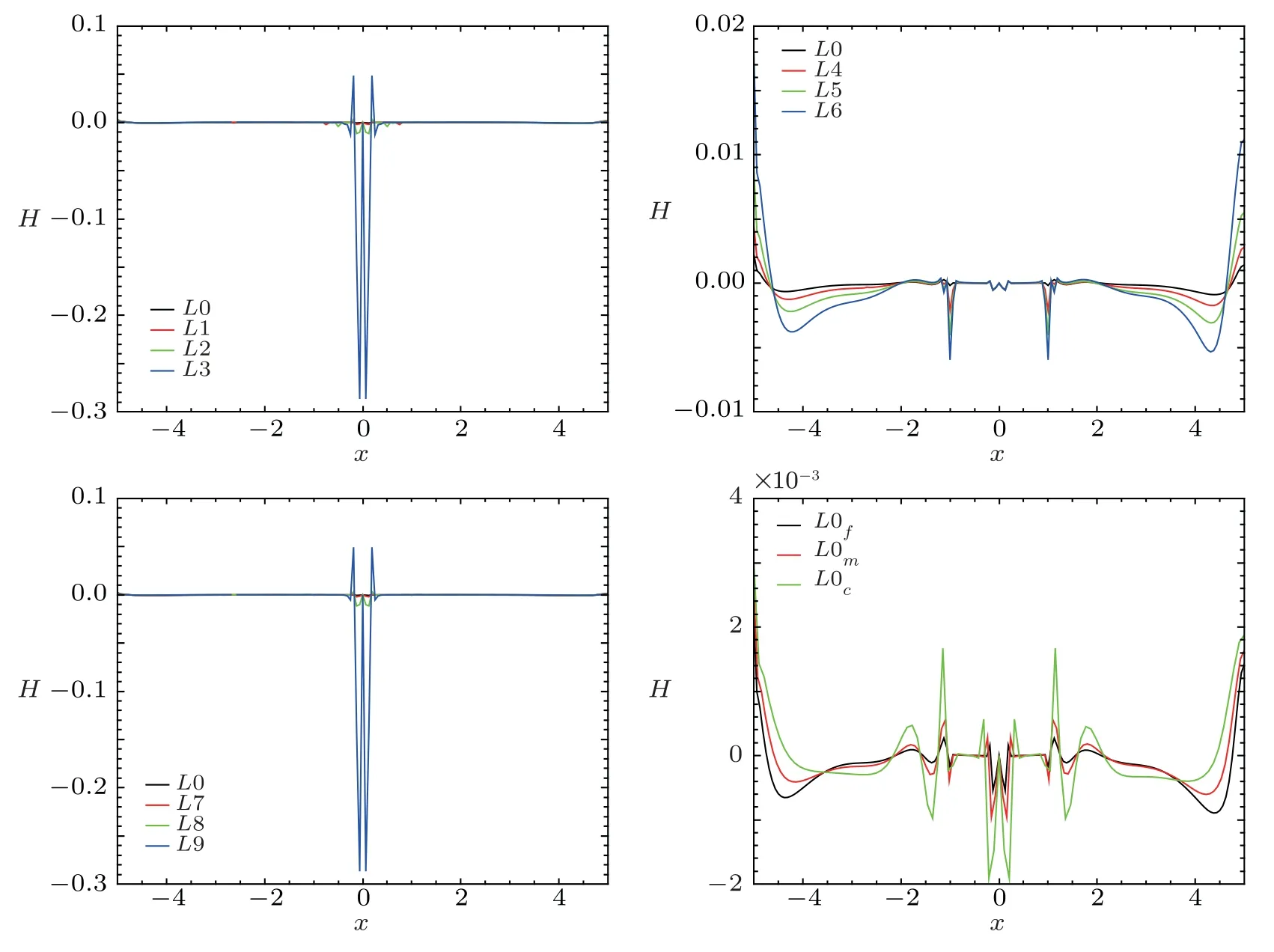
Fig.3 The initial Hamiltonian constraint violation of PBHLs.
where the evolution ofαis given by

And the proper length measured in a cctk-delta-time (or a timestep) is then given by

whereβi(τ,x) is the shift vector obeying a Gamma driver andγτis a constant-τedge parameterized byℓ.
Figure 4 shows the expansion of four PBHLs with the smallest initial Hamiltonian constraint violation in each group,where a prime represents a derivative with respect to the proper timeτ.We can see that L0 and L1 evolve differently even though they share a sameρt.That is to sayfPBHwill play an important role during the evolution of PBHLs.Comparing L4 to L0 and L1,we find that the PBHL with a largerρtno matter due to an extraρmor a largermPBHexpands faster.There is no intersection point between the evolutions ofDedge(τ)′,which means a PBHL with a larger−Kcwill keep expanding faster for ever.Finally,we also find that the motion of PBHs caused by the expansion of PBHLs does occur at speeds close to that of light.
Figure 4(b)shows the expansion of L0 and Fig.5 shows the L2 norms of the Hamiltonian and momentum constraint for L0 with spacing of the finest one of 5 refinement levels equal to 0.0625,0.078 125 and 0.104 166 7 respectively.They serve as a convergence test for evolving PBHLs.
3.2 Gravitational Waves in Primordial Black Hole Lattices
We have shown that the motion of PBHs caused by the expansion of PBHLs occurs at speeds close to that of light.Here we will use both analytical estimates and numerical simulations to cross check the production of GWs in expanding PBHLs.
(i) Theoretical Estimation
The total energy radiated by one PBH in an expanding PBHL betweenτandτ+∆τcan be considered as the gravitational radiation from an accelerated mass estimated by[27]

Fig.4 Expansion of four PBHLs with the smallest initial Hamiltonian constraint violation in each group.

Fig.5 L2 norms of the Hamiltonian and momentum constraint for L0 with spacing of the finest one of 5 refinement levels equal to 0.0625,0.078 125,and 0.104 166 7 respectively.
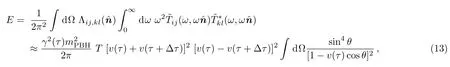
where the energy-momentum tensor is
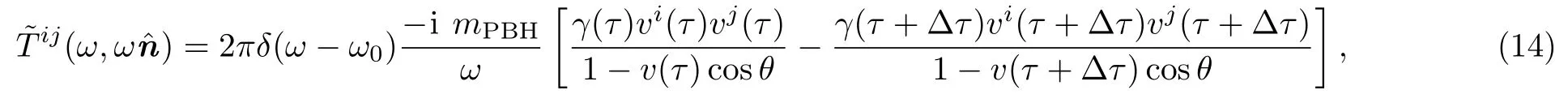
the Lambda tensor Λij,kl() is
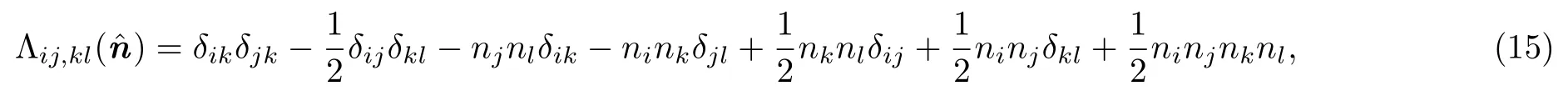
the scalar product of the direction of gravitational radiationand the velocity of PBHvisnivi=vcosθ,ω0is the frequency of the gravitational radiation atτ,T=2πδ(0)≈∆τandγ=(1−v2)−1/2.The term of [v(τ)−v(τ+∆τ)]2predicts that,in our PBHLs,the total energy radiated whenτ14 is larger than that whenτ14 because|Dedge(τ14)′′|is much larger than|Dedge(τ14)′′|as shown in Fig.4.The term of[v(τ)+v(τ+∆τ)]2predicts that whenτh14 the total energy radiated in L4 should be larger than that in L0 and L7 becauseDedge(τ)′of L4 is larger than that of L0 and L7.Similarly,according to the initial distribution ofK=KcW(r),the total energy radiated in PBHLs should not be uniform and the locations far away from the center are full of more radiation energy.
(ii) Simulation Results

Fig.6 A sample of GWs emitted in expanding PBHLs,as estimated by the Newman-Penrose scalar Ψ4.
Figure 6 shows the waveforms of GWs,as estimated by the Newman-Penrose scalar,produced at several distancesrin expanding PBHLs with differentρt.As shown in Ref.[28],for binary mergers,people can recover the strainhfrom the Newman-Penrose variable Ψ4after multiple integrations in time by choosing the integration constants such that the signal is zero at late times after each integration.In our case,however,the waveform is produced during the whole simulations.Therefore,we can not choose the integration constants after each integration and recoverhfrom Ψ4.Forτ14,there is an obvious production of GWs and we also find an obvious deceleration in Fig.4;forτ14,the amplitude of waveforms decreases and there is a plateau forDedge(τ)′in Fig.4.That is to say,there are some gravitational potential energy among PBHs converted to the GWs radiation andThe amplitude of waveforms increases withρtincreasing,which also means
The right plots in Fig.6 show the waveforms of GWs produced at several distancesrin L0.The oscillations due to numerical error atτ ≈35 inL0cdisappear inL0f,which guarantees the other oscillations in Fig.6 are the waveforms of GWs produced in expanding PBHLs.
4 Summary and Discussion
In this paper,we first use the wide-used Einstein Toolkit to solve the Einstein constraints of PBHLs with different value ofmPBHandfPBHwhich is determined by the surrounding flat-distributed dust with energy densityρm.From the solutions,we find that a smaller PBH massmPBHgives a shorter initial proper cubic edgeDedge(τ=0)and leads a lower initial expansion rate−Kc;a higher matter energy densityρmhas a higher initial expansion rate−Kcbut produces a shorter initial proper cubic edgeDedge(τ=0); a larger PBH massmPBHand a smaller matter energy densityρmstill produce a larger initial proper cubic edgeDedge(τ=0)but lead a lower initial expansion rate−Kc; a smaller PBH massmPBHviolates the Hamiltonian constraint more severely; the PBH with larger mass will be gravitationally coupled to its neighbors more tightly; the matter surrounding the PBH suppresses the gravitational correlation among PBHs.
And then we simulate the expansion of PBHLs with the smallest initial Hamiltonian constraint violation in each group.From the evolutions,we find thatfPBHplays an important role during the evolution of PBHLs; the PBHL with a largerρtno matter due to an extraρmor a largermPBHexpands faster; a PBHL with a larger−Kcwill keep expanding faster for ever; the motion of PBHs caused by the expansion of PBHLs does occur at speeds close to that of light.Meanwhile,we use both analytical estimates and numerical simulations to cross check the production of GWs in expanding PBHLs and find that
Comparing with the black hole and neutron star binaries’ coalescence,there is an abnormal feature that the amplitude of GWs does not decrease with radius but increase with radius in expanding PBHLs.Our explanation is that the final waveform of GWs at any location is the superposition of eight waveforms of GWs produced by eight adjacent PBHs in expanding PBHLs and every waveform of GWs obeys the theoretical estimation (13).
There is one caveat: the total energy densityρtof the real Universe in matter dominated era is much smaller than our exaggerated initial values∼10−3.As we know,in SI units,this value corresponds to 6.1727·1017kg/m3henceH2=3.45·1047km2/s2/Mpc2.Although we can suppressρtthrough enlarging the volume of our cubic until a reasonableρtcompared to the real Universe in dominated matter era,we can not afford the accompanying high computational cost.Therefore,we would not give the forecast whether GWs detectors can detect such signals presented in our paper or not in future.
Acknowledgment
We would like to thank Xiao Guo and You-Jun Lu for their helpful discussions and advices on this paper.
 Communications in Theoretical Physics2019年10期
Communications in Theoretical Physics2019年10期
- Communications in Theoretical Physics的其它文章
- Superstatistics of Modified Rosen-Morse Potential with Dirac Delta and Uniform Distributions
- Design of Tunable Devices at Terahertz Frequencies Based on Quasi-Photonic Crystals Incorporated with Graphene
- Coupling Instability of a Warm Relativistic Electron Beam with Ion-Channel Guiding
- Modeling of Neurodegenerative Diseases Using Discrete Chaotic Systems
- Gravitational Deflection of Massive Particles by a Schwarzschild Black Hole in Radiation Gauge∗
- Magnetic Properties of an Antiferromagnetic Spin-1/2 XYZ Model in the Presence of Different Magnetic Fields: Finite-Size Effects of Inhomogeneity Property∗
