Fifth-Order Alice-Bob Systems and Their Abundant Periodic and Solitary Wave Solutions∗
Qi-Liang Zhao (赵启亮), Man Jia (贾曼), and Sen-Yue Lou (楼森岳),2
1School of Physical Science and Technology,Ningbo University,Ningbo 315211,China
2Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China
Abstract The study on the nonlocal systems is one of the hot topics in nonlinear science.In this paper,the well-known fifth-order integrable systems including the Sawada-Kotera(SK)equation,the Kaup-Kupershmidt(KK)equation and the fifth-order Koterweg-de Vrise (FOKdV) equation are extended to a generalized two-place nonlocal form,the generalised fifth-order Alice-Bob system.The Lax integrability of two sets of Alice-Bob systems for all the SK,KK and FOKdV type systems are explicitly given via matrix Lax pairs.ThePT symmetry breaking and symmetry invariant periodic and solitary waves for one set of nonlocal SK,KK and FOKdV system are investigated via a special travelling wave solution ansatz.
Key words: Alice-Bob SK equarions,Alice-Bob KK equations,periodic and solitary waves
1 Introduction
The nonlinear Schrodinger (NLS) equation has been successfully extended to some nonlocal forms because of the work of Ablowitz and Musslimani in 2013.[1]The possible applications of nonlocal systems for two-place physics(Alice-Bob physics) was proposed by one of the authors(Lou).[2]In Ref.[1],the nonlocal NLS system is written as

In this paper,we focus on the possible nonlocal extensions on the well known fifth-order nonlinear systems such as the Sawada-Kotera (SK) equation,the Kaup-Kupershmidt (KK) equation and the fifth-order Koteweg de-Vrise (FOKdV) equation.In Sec.2,we directly write down a fifth-order Alice-Bob(AB)system by means of the parity and time reversal symmetries.In Sec.3,we select out some integrable fifth-order AB systems from the general AB system of Sec.2 by fixing model parameters.In Sec.4,the abundantsymmetry breaking andinvariant periodic and soliton solutions are studied for integrable fifth-order AB systems.The last section is devoted to do some short summary and discussion.
2 Fifth-Order Alice-Bob Systems
The generalized homogeneous fifth-order nonlinear system possesses the form[15]

which is a generalization of the well known SK equation(a=b=c=5),

the KK equation (a=20,b=25,c=10),
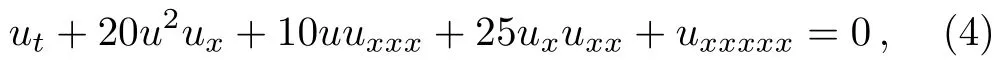
and the FOKdV equation (a=30,b=20,c=10),
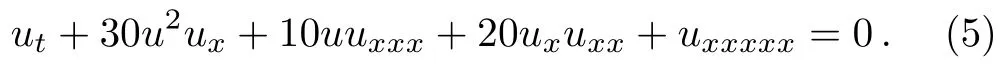
The possible physical applications of the generalized fifthorder nonlinear system (2) can be found in many natural scientific fields such as the ocean gravity waves (surface and internal waves),[16]plasma waves,[17]electromagnetic waves[18]and so on.
The fifth-order nonlinear system (2) can be extended to a nonlocal two-place form
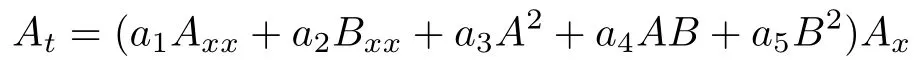

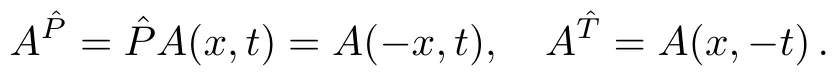
For,the model (6) is equivalent to the local system (2).
To solve a nonlocal system,one of the simplest methods is the symmetric-antisymmetric separation approach with respect to the operator.For the operatorwith=1,any functionAcan be separated to symmetry partuand antisymmetry partv,
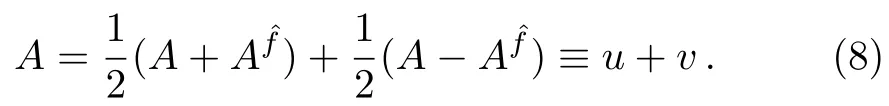
Because of the property (8),the nonlocal system (6) can also be separated to symmetric part (u3x ≡uxxx,u5x ≡uxxxxx,v3x ≡vxxx,v5x ≡vxxxxx),
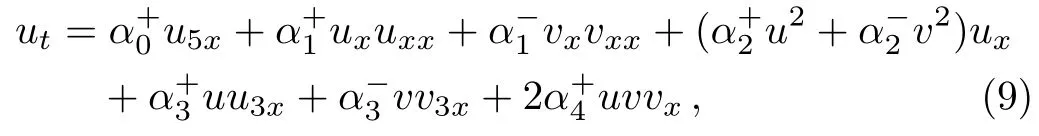
and antisymmetric part,
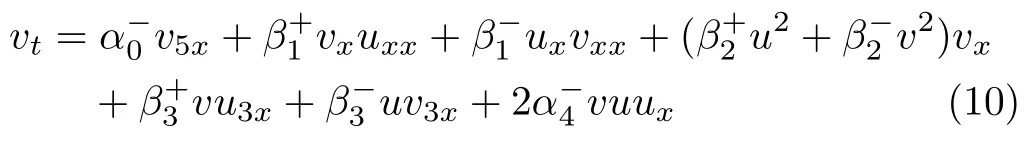
with the constant relations
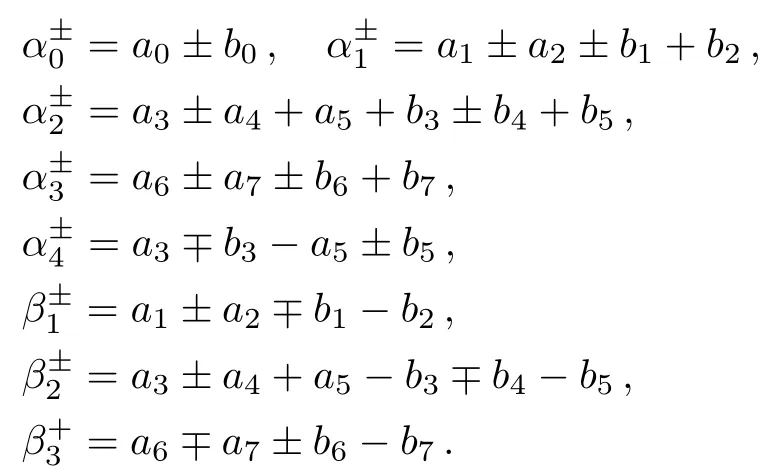
Thus,to solve the nonlocal system (6) is equivalent to solve the local coupled system (9) and (10) with the invariant conditions
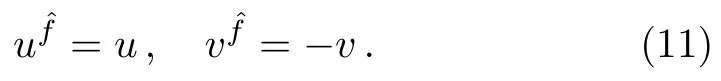
In other words,the nonlocal equation (6) is ansymmetry reduction of the coupled local system (9) and(10).
3 Integrable Fifth-Order Nonlocal Systems
Because the nonlocal system (6) is only a symmetry reduction of Eqs.(9) and (10),Eq.(6) is integrable if the coupled system (9) and (10) is integrable.Thus,in this section,we list some special Lax integrable cases of Eq.(6).
3.1 Lax Integrable ABSK Systems
It is known that the local SK system (3) possesses the scalar Lax pair[19]
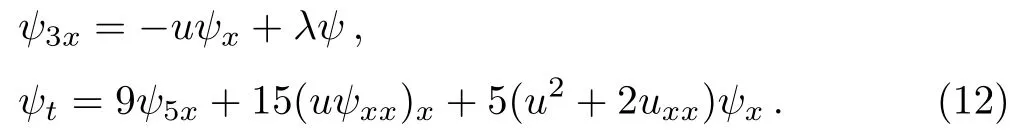
Now if we extend the scalar Lax pair (12) to matrix Lax pairs,we can find some types of nonlocal ABSK systems.Here,we write down two special forms.The first Lax integrable ABSK system can be obtained from Eq.(12) by taking the transformation
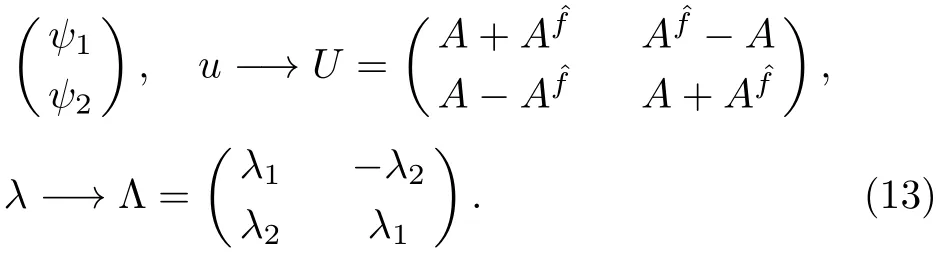
The integrable ABSK related to the Lax pair (12) with(13) possesses the form (B==A(−x,−t),u=A+B,v=A −B)

The second Lax integrable ABSK system can be obtained from Eq.(12) by taking the transformation

The integrable ABSK related to the Lax pair (12) with(14) possesses the form (B==A(−x,−t),u=A+B,v=A −B)

3.2 Lax Integrable ABKK Systems
For the local KK system (4),the Lax pair possesses the form

Similar to the nonlocal SK cases,some types of the Lax integrable nonlocal ABKK systems can be obtained from transform the scalar Lax pair (17) to matrix Lax pair.For instance,the integrable ABKK system (B=AP T=A(−x,−t),u=A+B,v=A −B)
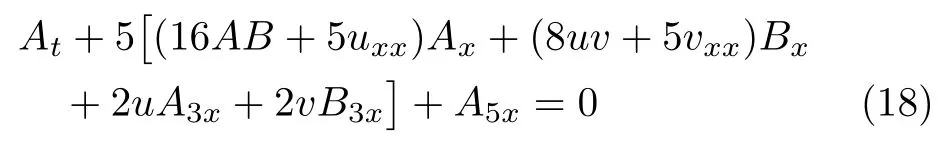
possesses Lax pair (17) with (13).
In the same way,(17) wirh (15) is a Lax pair of the following Lax integrable ABKK equation,
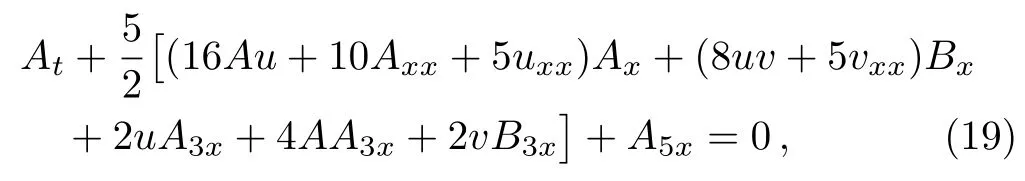
whereB=AP T=A(−x,−t),u=A+B,v=A −B.
3.3 Lax Integrable Fifth-Order ABFOKdV Systems
The Lax pair of the FOKdV equation(5)possesses the form
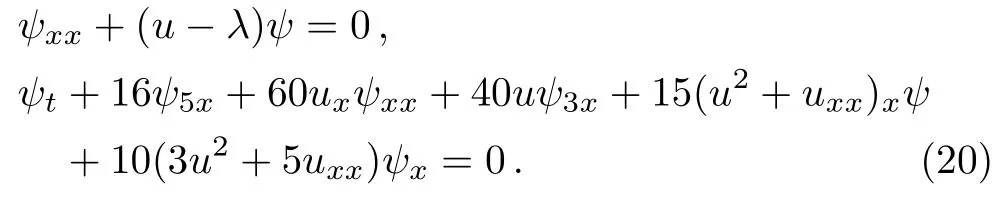
If we change the Lax pair (2) to a matrix form via (20),we can obtain an ABFOKdV system
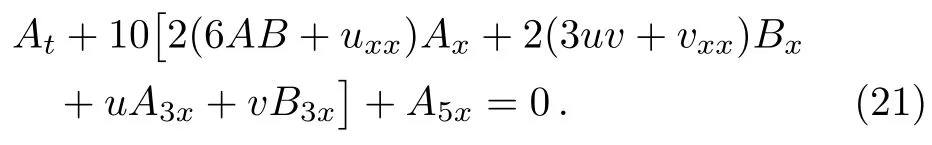
From the Lax pair (20) with (15),we can find another ABFOKdV equation
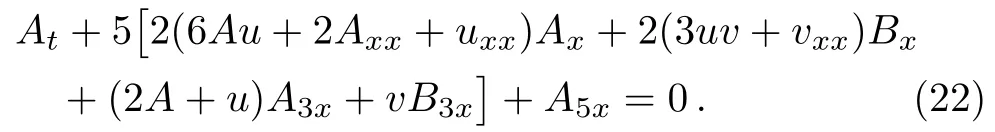
3.4 Integrable Fifth-Order Systems Related to Linear Couplings
From the equations (9) and 910),it is straightforward to find that when

i.e.,

one can find three integrable cases which can be uniformly written as
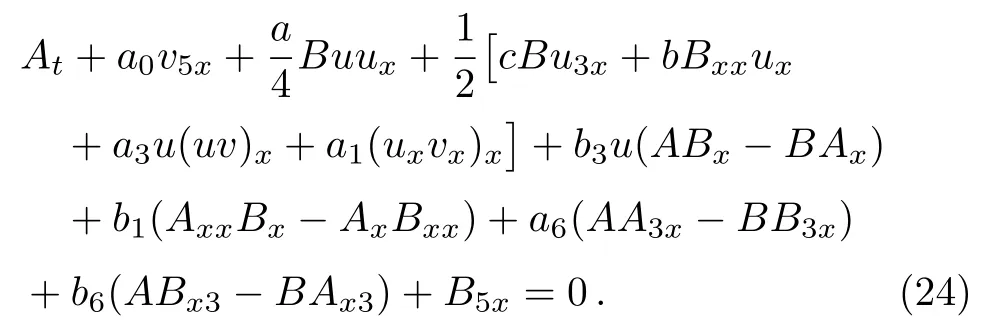
Equation (24) may be integrable if the constants{a,b,c}are fixed as same as those of Eqs.(3),(4),and (5) while other constantsa0,a1,b1,a3,b3,a6andb6are remained free.
More especially,by appropriately taking the arbitrary constants in Eq.(24),we have
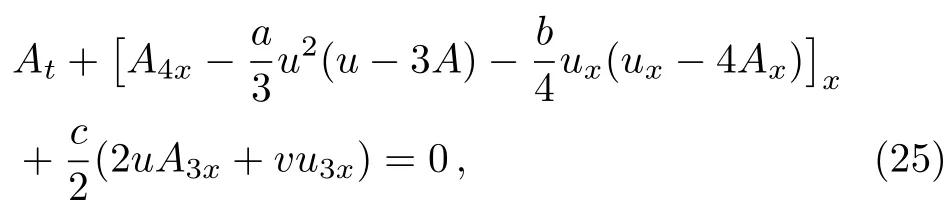
which includes three special cases (16),(19),and (22)when the constantsa,bandcare fixed as the same as in Eqs.(16),(19),and (22).
4 Abundant Periodic and Solitary Waves of Fifth-Order Nonlocal Systems
In this section,we focus our attention on the periodic and solitary waves for the significantly integrable systems,the ABSK system (16),the ABKK system (19) and the ABFOKdV system (22).
To find the periodic waves and solitary waves of the systems(16),(19),and(22),one can uniformly treat them for Eq.(25) in the special traveling wave ansatz
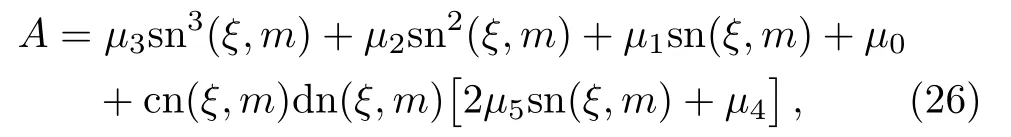
whereξ=kx+ωt,k,ω,m,µi,i=0,1,...,5 are arbitrary constants and sn(ξ,m),cn(ξ,m) and dn(ξ,m) are Jacobi elliptic functions with modulusm.
Substituting the solution ansatz to the model equation and vanishing all the coefficients of the elliptic Jacobi functions,we get sixteen relations among the solution parameters{k,ω,m,µi,i=0,1,...,5}and the model parameters{a,b,c},

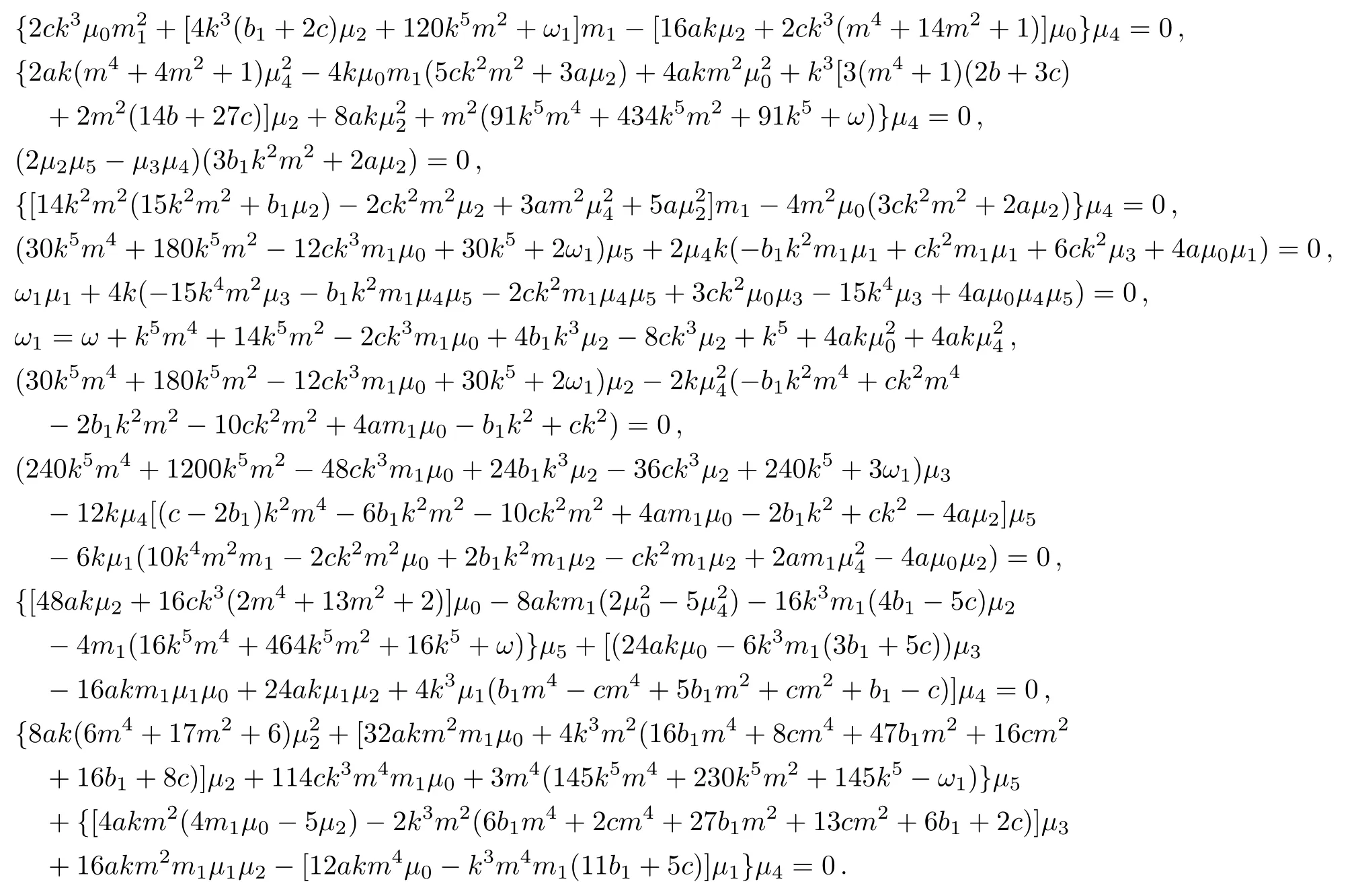
There are many special solutions for the above nonlinear algebraic solutions.In the following three special subsections,we list the final periodic solutions according to the special solutions of the above parameter constraints for the ABSK equation (16) (a=b=c=5),the ABKK equation (19) (a=20,b=25,c=10) and the ABFOKdV equation (22) (a=30,b=20,c=10).
4.1 Periodic and Solitary Waves of the Integrable ABSK System (16)
For the ABSK system (16),there are five independent periodic solutions,A=Ai,i=1,2,...,5 with notationsS ≡sn(ξ,m),C ≡cn(ξ,m),D ≡dn(ξ,m) andξ ≡kx+ωt+ξ0and arbitrary constantsk,m,µ,νandξ0,,

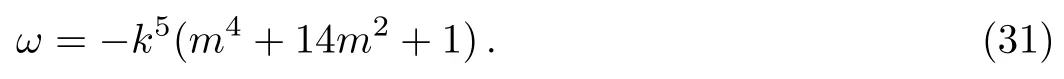
From the solutions (27)–(31) we know that allAi,i=1,...,5,are generally thesymmetry breaking periodic wave solutions whileAi(µ=0),i=1,2,3,4 andA5(µ=0,ν=0)are related to the ˆPˆTinvariant periodic waves.
It is clear that all the periodic wavesAi,i=1,...,5,will be reduced to the solitary waves or the vacuum (constant)solutions.Two independent solitary wave solutions,As1andAs2,possess the following forms after using the redefinitions of constants,
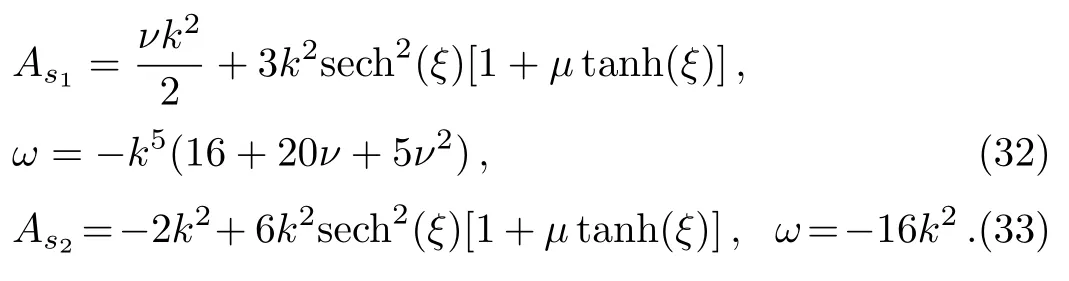
The solitary wave solution (32) may have zero boundary condition by takingν=0 atξ=±∞,however,the solitary wave solution (33) possesses always nonzero boundary atξ=±∞and the nonzero boundary is dependent on wave numberk.
4.2 Periodic and Solitary Waves of the Integrable Nonlocal ABKK System (19)
For the ABKK system (19),there exist four independent ˆPˆTsymmetry breaking periodic wave solutions,
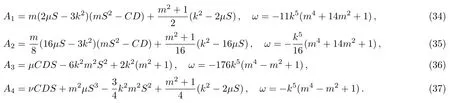
In some special cases,µ=0 for Eqs.(34),(35),(36),and andµ=ν=0 for Eq.(37),the periodic waves becomeinvariant waves.
When the modulusmof the Jacobi elliptic functions are taken as±1,all the periodic waves (34),(35),(36),and(37) are reduced to solitary wave solutions or the constant vacuum solutions.
Two independent solitary wave solution possess the forms,
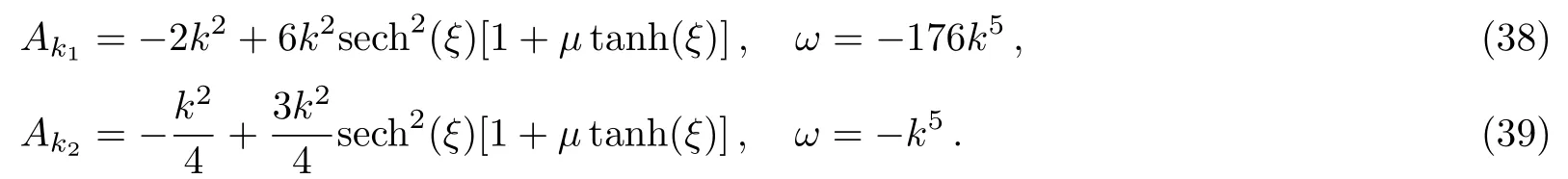
It should be mentioned that both the solution (38) and (39) do not have the zero boundary at±∞.The nonzero boundaries arek-dependent.
4.3 Periodic and Solitary Waves of the Nonlocal Integrable ABFOKdV System (22)
For the ABFOKdV system (22),the independent fivesymmetry breaking periodic wave solutions possess the forms for nonzeroµ,
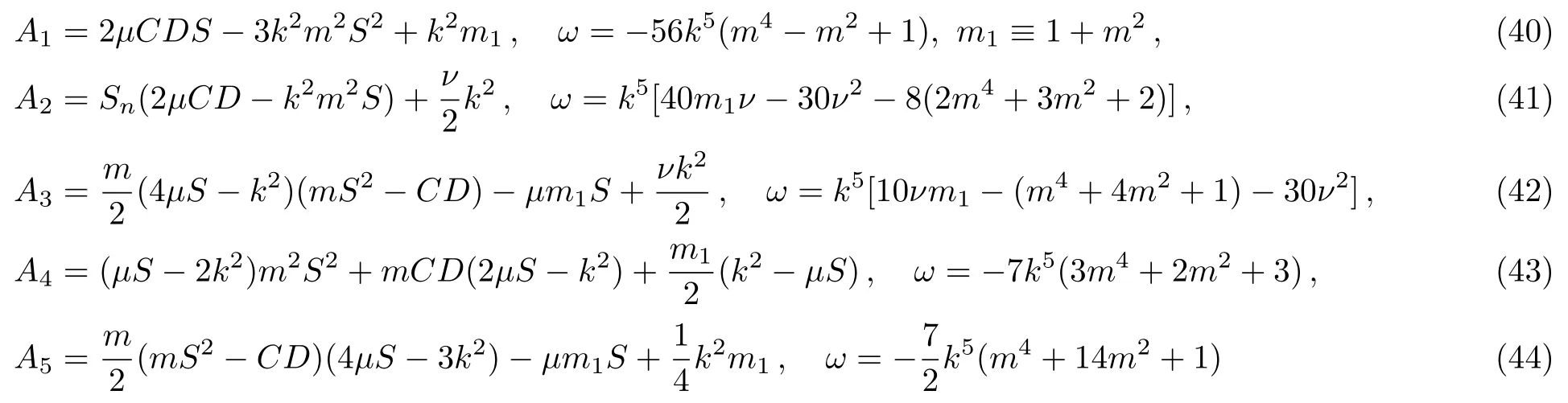
with arbitrary constantsk,m,µandν.
When the constantsµin the periodic wave solutions are fixed asµ=0,all thesymmetry breaking periodic waves (40)–(44) becomeinvariant periodic wave solutions.When the modularm=1,we get two independent soliton solutions (ξ=kx+ωt),
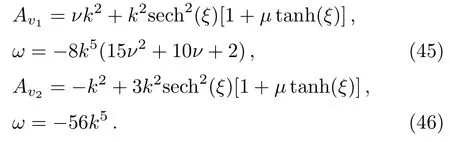
It is clear that the soliton solution (45) may have zero boundary conditions atξ →±∞by takingνwhile the second soliton solution (46) always possesses the wave numberkdependent boundary condition.
5 Summary And Discussions
In this paper,we focus on the Alice-Bob nonlocal fifthorder integrable and nonintegrable systems.By using the well known parity and time reversal symmetries,a quite general two-place nonlocal fifth-order system (6).Especially,the nonlocal fifth-order system(6)including at least two types of Lax integrable ABSK systems,two types of Lax integrable ABKK systems and two types of Lax integrable ABFOKdV systems.
By studying the travelling wave solutions for one type of nonlocal SK,KK and fifth-order KdV systems,one can find that there are abundantsymmetry breaking and symmetry invariant periodic waves which includes two types of solitary waves for all three models.Apart from the periodic waves and soliton solutions,many kinds of nonlinear excitations (such as the multiple solitons,breathers and rogue waves) for various nonlocal systems(nonlocal NLS,MKdV,KdV,KP and DS systems) have been obtained by a number of researchers.[1−9,20−27]The more about these kinds of solutions on the the fifth-order integrable nonlocal Alice-Bob systems should be further studied.
 Communications in Theoretical Physics2019年10期
Communications in Theoretical Physics2019年10期
- Communications in Theoretical Physics的其它文章
- Superstatistics of Modified Rosen-Morse Potential with Dirac Delta and Uniform Distributions
- Design of Tunable Devices at Terahertz Frequencies Based on Quasi-Photonic Crystals Incorporated with Graphene
- Coupling Instability of a Warm Relativistic Electron Beam with Ion-Channel Guiding
- Modeling of Neurodegenerative Diseases Using Discrete Chaotic Systems
- Gravitational Deflection of Massive Particles by a Schwarzschild Black Hole in Radiation Gauge∗
- Magnetic Properties of an Antiferromagnetic Spin-1/2 XYZ Model in the Presence of Different Magnetic Fields: Finite-Size Effects of Inhomogeneity Property∗
