基于长短期记忆神经网络的风力发电功率预测方法
李相俊,许格健
基于长短期记忆神经网络的风力发电功率预测方法
李相俊,许格健
(新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司),北京市 海淀区 100192)
风力发电过程具有较强的随机性,导致风力发电功率的预测准确度不高。针对上述问题,提出了一种融合深度学习算法的风力发电功率预测方法。以历史风力发电功率数据作为输入,建立风力发电功率预测模型,实现对未来一个时间刻度的风力发电功率预测。算例结果表明,与传统时序预测方法相比,基于长短期记忆神经网络的风力发电功率预测结果在各项指标中误差更小,验证了上述方法在风力发电功率预测中的可行性和有效性,提升了风力发电功率预测的准确性。
深度学习;时序预测;风力发电;长短期记忆神经网络
0 引言
随着能源与环境问题的日益突出[1],风能作为一种无污染、可持续的清洁能源成为了能源发展的关注点。国内风力发电水平也保持着稳步增长,2018年风力发电量达到了3 660亿kW·h,占全部发电量的5.2%[2]。在风力发电规模稳步增长的同时,其本身存在的问题也被逐渐放大。由于受多种环境因素的影响,风力发电的波动性及随机性[3-5]成为了制约其发展的重要因素。为了解决这一问题,需进行风力发电功率预测研究,以判断其变化趋势并提前采取相应措施。
物理模型预测方法与数据模型预测方法是目前针对风力发电功率预测的两大主要方法。物理模型预测方法主要考虑数值天气预报(numerical weather prediction,NWP) 及其他多种因素的影响。基于该方法的风力发电功率预测需要较多的参数,如历史数据、地形地貌、气象数据等[6-13],导致其在短期预测能力上表现较为一般,其结果更适合作为长期预测的参考标准。
数学模型预测方法是目前研究最广泛的风力发电功率预测方法,在数学预测模型中,针对风力发电功率的预测分为2种形式。一种预测方法是考虑多种因素对风力发电功率的影响,通过建立数学模型得到相应的非线性回归曲线,并依此进行风力发电功率预测。传统的数学模型预测方法,如小波算法(wavelet)[14-15]、支持向量机(support vector machine,SVM)[16]等,都是基于风力发电功率的相关特征进行短时预测,通过对影响风速以及风电力发电功率的特征进行分析,预测未来一段时间内的风力发电功率。另一种预测方法是不考虑其余环境条件的影响,只考虑风力发电功率本身随时间变化的特性趋势,并依此进行风力发电功率时序预测分析。自回归移动平均(autoregressive moving average,ARMA)模型[17]是时序预测的主要应用算法,通过量化当前数 据与之前数据的关系,同时解决随机变化项的 求解问题,进一步求得需求预测的下一时刻 数据。
除传统预测方法外,人工神经网络也常应用于风力发电功率的短时预测中。由于神经网络形式多样,其对应的预测方法也不同。如李彬等[18]提出了基于人工神经网络的预测方法,以多种特征因素作为神经网络输入,预测得到其当月的风力发电功率概率分布曲线。江岳春等[19]将传统BP神经网络与多种算法相结合,对风力发电功率的时间序列进行短时时序预测,取得了良好的预测效果。由于神经网络出色的非线性数据拟合能力,在许多针对风力发电功率的短时及超短时预测方法中,都会应用神经网络算法对历史数据进行分析,再采取其余预测方法进行风力发电功率及其分布概率的预测[20-24]。
随着人工智能及深度学习的不断推广应 用[25-26],各种针对不同数据的深度学习算法逐渐成为各领域专家关注的焦点,也在新能源领域得到了广泛的应用[27-28]。其中循环神经网络(recurrent neural networks,RNN)作为深度学习中一种典型的序列分析模型,在语言翻译、流量预测等方面都得到了广泛的应用。但在应用过程中,RNN算法的序列数据处理能力在面对大规模数据进行跨度较大的序列预测时,易出现梯度消失和梯度爆炸的问题。在RNN的发展过程中,一种特殊的循环神经网络结构,即长短期记忆(long short-term memory,LSTM)神经网络结构,很大程度上解决了这一问题,更加适用于数据规模较大的序列数据[26],并且在预测精度上有着良好的表现。但是该方法在风力发电功率预测方面的应用国内外鲜见报道。
本文提出一种基于 LSTM神经网络的风力发电功率时序预测方法,采用某风电场的发电数据进行时序预测分析,并与传统时序预测方法进行对比分析。结果表明,该方法可有效提高风力发电功率的预测精度,并且针对不同规模数据均有良好的预测效果。
1 时序预测方法
1.1 差分整合移动平均自回归模型
在传统时序算法中,差分整合移动平均自回归(autoregressive integrated moving average,ARIMA)算法是一种常用的时序预测算法[29-31],该算法通过将ARMA模型与差分模型相结合,提升了原有算法的时序预测能力。ARIMA算法主要分为3部分:1)通过自回归(autoregressive,AR)模型描述当前值与历史值之间的关系;2)用变量自身的历史时间数据对自身进行预测;3)通过移动平均法(moving average,MA)消除预测中的随机波动,并通过适当的差分次数使数据序列更加平稳。
在ARIMA模型中,AR模型可表示为:
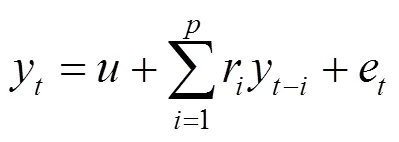
式中:y表示当前值;与r分别为常数项与常系数;e为误差;为阶数,表示以之前多少历史值为参考。在AR模型中,主要关注的是当前值与历史值之间的关系。
在ARIMA模型中,MA模型可表示为:
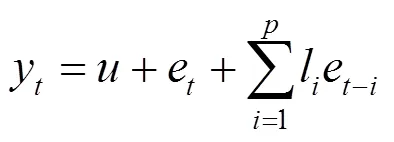
式中:l为常系数。在MA模型中,主要关注的是计算当前值的过程中误差的累加。
将AR模型与MA模型相结合所得即为ARMA模型,通过2种模型的结合,可观测到在一组时间序列中稳定因素的趋势与作为波动因素的误差趋势,将两者相结合即可预测未来时刻会出现的数值,即

在ARIMA模型中,为了保证序列数据的平稳,添加了差分模型对原有数据进行差分运算,整体运算过程仍满足ARMA模型的运算方法。由于其本身以历史数据预测自身的特性,因此常用于能源领域的时序功率预测。ARIMA在计算过程中要经过复杂的数据处理过程,而且由于本身对输入数据的要求,其对个别输入数据无法识别,导致其应用受到了一定程度的限制。
1.2 LSTM神经网络模型
1.2.1 LSTM神经网络单元
深度学习中的LSTM神经网络本质上是循环神经网络的一种,与普通循环神经网络所不同的是,LSTM神经网络是一种时间尺度较长的短时记忆网络。其主要运算方法仍是基于循环神经网络的“记忆”基础,其网络结构虽然与循环神经网络结构相似,但其内部构成及运算更加复杂。
LSTM神经网络单元结构如图1所示,其网络单元相较于传统循环神经网络运算方法的优势在于其特殊的“遗忘”过程,该过程确保LSTM神经网络可以进行时间跨度更长的预测。

图1 LSTM神经网络单元结构
LSTM神经网络的遗忘率是由前一时刻的输出与该时刻网络的输入共同计算得出的,计算方法如下:

以和分别为权重及截距,将-1时刻的神经网络输出-1与时刻的输入数据相结合进行线性变换。表示sigmoid激活函数,通过sigmoid激活函数将线性变换结果映射为0~1的衰减函数,得到f。
在计算遗忘率后,需进行同一时刻输入的记忆运算。所需的衰减系数记为,当前的记忆状态记为¢,其对应的求取方法为:
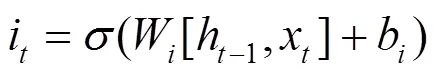

式中:W、W为权重;b、b为截距。
1.2.2 LSTM神经网络结构
LSTM神经网络进行预测通常有2种方法:1)与传统深度神经网络相似的反向传播误差算法,这种方法考虑多因素输入,在不同时刻将LSTM展开为随时间推移的深度神经网络;2)只考虑单一时序序列的实时递归学习算法。在应用上,2种方法各有优势。本文的预测过程是基于时序算法的风力发电功率预测,由于只考虑单一变量的时序变化,因此主要应用实时递归学习算法。
在实时递归学习算法中,以1.2.1中所述的神经网络单元结构为LSTM基本网络单元,生成的神经网络单元的连接形式与输入形式如图2所示。

图2 LSTM神经网络结构
图2中,神经网络在每个时刻都进行数据输入,经过“遗忘”与“记忆”的处理后,保留-1时刻数据特征C-1,并结合时刻的输入数据x计算本时刻的数据特征,记作C,其对应的计算公式为:
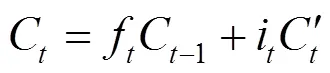
求取时刻的数据特征后,进行LSTM神经网络本身记忆阶段的算法实现。时刻的记忆输出记为h,与之前所求取遗忘部分的衰减系数相似,计算得到输出门的衰减系数:
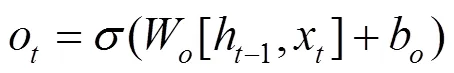
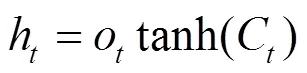
2 LSTM网络风力发电功率预测
由于LSTM网络的结构需求,在进行预测分析之前,需先进行输入数据的预处理以及LSTM神经网络超参数设定。
2.1 数据预处理
使用风力发电功率数据进行时序预测时,考虑到神经网络预测模型中使用的非线性激活函数的输入、输出范围,为避免神经元饱和,需要对风力发电功率数据进行归一化处理。本文所采用的归一化标准为最小、最大值标准化方法,其对应的公式如下:
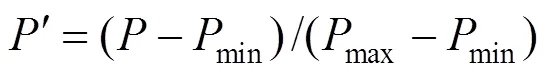
式中:为当前时刻的风力发电功率数据值;min、max分别为所有数据中风力发电功率的最小值、最大值;¢为求得的风力发电功率归一化结果。
在数据输入阶段完成归一化后,对实际输出的预测数据需应用归一化还原函数将数据还原至其原有大小,最小、最大值标准化方法对应的还原函数为:

式中:¢pre为未经还原的LSTM神经网络预测输出值;pre为还原后的风力发电功率预测值。
数据输入阶段除了对数据进行归一化处理之外,还要对输入数据进行数据分类处理。风力发电功率数据分为训练集和测试集2个集合。通过训练集数据对LSTM神经网络进行训练,在训练的过程不断优化神经网络结构及内部参数,再用测试集数据测试训练后的LSTM神经网络的预测效果。
2.2 确定LSTM神经网络超参数
在建立 LSTM 神经网络时序风电预测模型的过程中,需进行LSTM神经网络超参数的设定。其中网络步长(epoch)以及隐层个数为神经网络结构参数,另外,为了防止网络出现过拟合,还需设定神经网络中神经元失活系数(dropout)与批尺寸(batch_size)。
在LSTM神经网络中,网络步长表示在神经网络运算过程中从输入到输出再返回输入的一次过程。随着步长的增加,神经网络的运算精度也得到提高,同时运算时间也会增加。在LSTM神经网络的数据输入阶段,输入维度表示每次运算输入数据的个数。神经元失活系数表示在进行神经网络运算的过程中,弃用其中一部分神经元进行计算的概率。通过应用该参数,取代了原本在神经网络中需要的正则化方法,也避免了过拟合的出现。在神经网络运算的过程中,通过设定适当的批尺寸,可以节省运算时间,避免全数据的同时计算。
2.3 风力发电功率预测
将经过归一化处理的风力发电功率数据作为LSTM神经网络的输入,以LSTM单元结构以及网络连接结构为基础,并完成LSTM神经网络超参数的设定,得到LSTM神经网络风力发电功率预测流程,如图3所示。其运算公式如下:
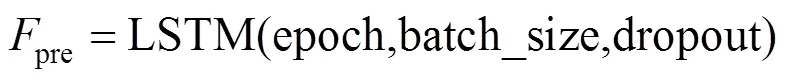
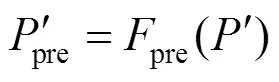
式中:pre表示LSTM神经网络预测模型;epoch,batch_size,dropout根据网络超参数确定。

图3 LSTM神经网络风力发电功率预测流程
¢由式(10)计算得出,为风力发电功率经数据预处理后所得结果,以¢作为输入求取对应的预测值¢pre。在进行预测的过程中,LSTM神经网络会根据设定的网络步长进行循环计算,不断更新LSTM神经网络内部参数在循环结束后,根据式(11)将输出结果还原为原有风力发电功率大小的pre,即为所求取的LSTM神经网络风力发电功率预测数据。
2.4 误差计算
本文选用2种不同的误差标准进行预测效果比较,其中一种误差标准为均方根误差(root mean squared error,RMSE),该误差标准可以表明预测值与真实值之间的偏差,其计算公式如下:
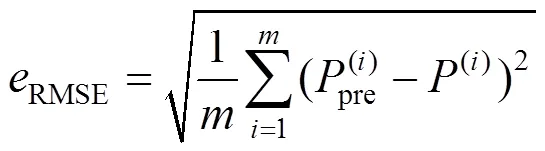
除了上述误差标准,本文同样选择了平均绝对误差(mean absolute error,MAE)作为另一种误差标准,对预测结果进行误差计算。与RMSE不同, MAE主要表现的是预测值误差的实际情况,其计算公式如下:

3 算例分析
3.1 实验设计
本文采用国内某风电场不同季节典型风力发电功率作为数据,数据采样时间间隔为1 min。数据总体为2类:1)一天24 h的风力发电功率数据;2)一周168 h的风力发电功率数据。通过2组不同规模的数据,与ARIMA算法分别进行预测精度对比,以验证LSTM神经网络在不同时间尺度以及不同数据规模下的预测效果。
为了优化神经网络运算效率及精度,在所应用的LSTM神经网络中,激活函数选择线性整流函数(rectified linear unit,ReLU),优化函数选择自适应矩估计(adaptive moment estimation,ADAM),网络训练过程中的误差函数选择均方误差(mean squared error,MSE)。
3.2 预测性能分析
分别采用ARIMA算法与LSTM神经网络进行春季日风力发电功率时序预测分析,并对所得的真实值与预测值进行对比。针对一天1 440个风力发电功率数据,本文将0:00—16:00的864个数据作为训练集,16:00—24:00的576个数据作为测试集,开展了2种方法的预测效果分析。图4为基于测试集数据得到的日风力发电功率ARIMA、LSTM神经网络预测结果,及应用2种方法的预测残差对比。可以看出,LSTM神经网络的时序预测结果在整体趋势上更接近风力发电功率真实值,且不会产生较大偏差,相较于传统ARIMA算法有更好的预测效果。
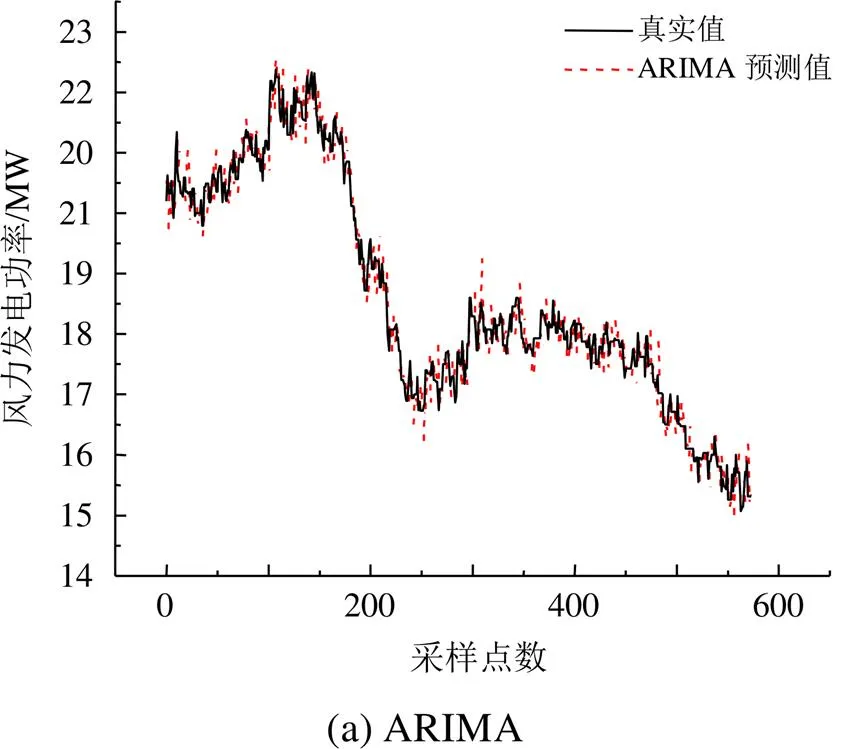
为了验证LSTM的预测能力,应用时间尺度更长的春季周风力发电功率曲线进行时序预测分析。针对一周10080个风力发电功率数据,本文将初始约100h的6048个数据作为训练集,后续约68h的4032个数据作为测试集,开展了预测效果分析。图5为基于测试集数据得到的周风力发电功率ARIMA、LSTM神经网络预测结果,及应用2种方法的预测残差对比。可以看出,由于训练数据增加,LSTM神经网络与ARIMA算法的预测效果均有明显提升;但LSTM神经网络的预测结果更符合原时序序列的趋势,且不会出现较大波动,在长时间序列的周数据预测中计算效果更好。应用式(14)、(15)分别对LSTM神经网络与ARIMA算法的预测结果进行了对比,如表1所示。在春季日风力发电功率曲线中,LSTM神经网络的2种预测误差RMSE、MAE比ARIMA算法分别降低了7.7%、7%。在数据规模更大的春季周风力发电功率曲线中,LSTM神经网络的2种预测误差RMSE、MAE比ARIMA算法分别降低了4.3%、3.1%。随着数据规模的增大,LSTM神经网络本身的预测性能也得到了提高。与春季日风力发电功率LSTM神经网络的预测误差相比,春季周风力发电功率预测误差RMSE降低了7.1%,MAE降低了12.5%。由此可知,在针对不同数据规模的风力发电功率预测中,深度学习算法均有良好表现,且随着数据规模的提升,可获得更好预测效果。
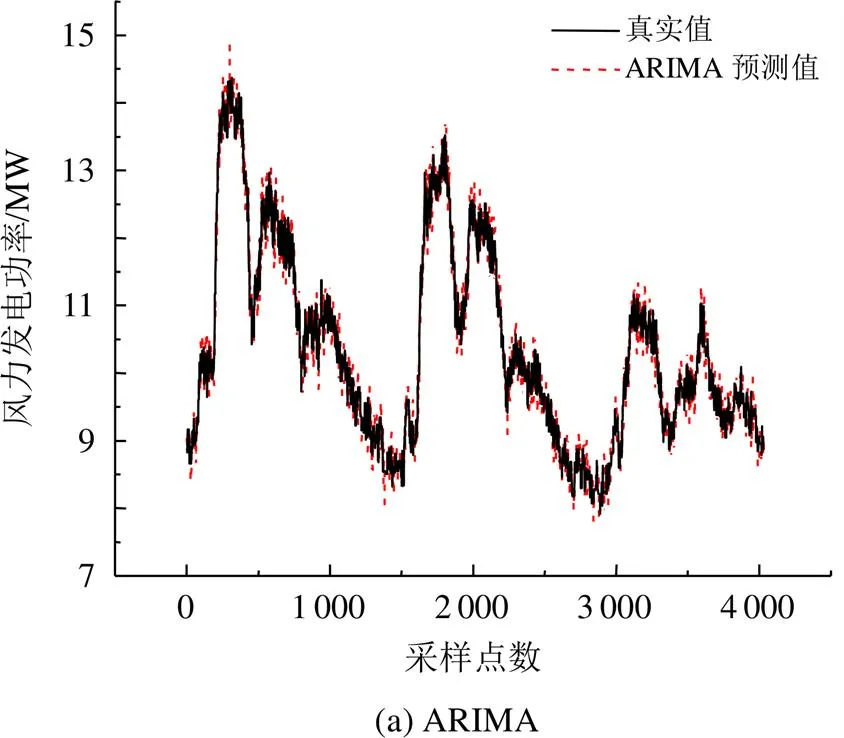
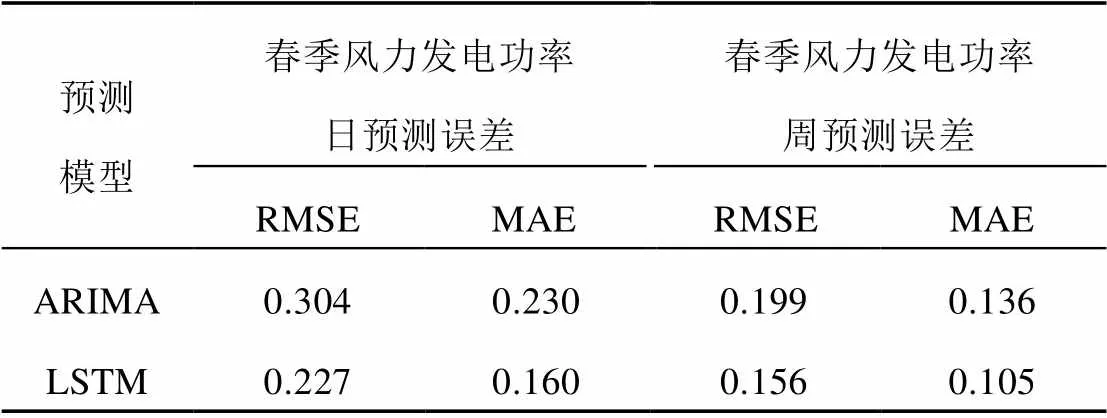
表1 基于LSTM神经网络与ARIMA算法的春季数据预测结果对比
3.3 四季风力发电功率预测分析结果
为了体现LSTM神经网络更优的预测效果,针对同一风电场的风电数据,选取另外3个季节的日风力发电功率数据与周风力发电功率数据进行了对比分析,如表2所示。可以看出,LSTM神经网络在各季节风力发电功率的时序预测结果中,相较于ARIMA算法的预测精度都有明显提升;同时随着数据规模变大,LSTM神经网络可以获得更好的预测结果,在短时数据基础以及长时数据基础中均有良好表现。
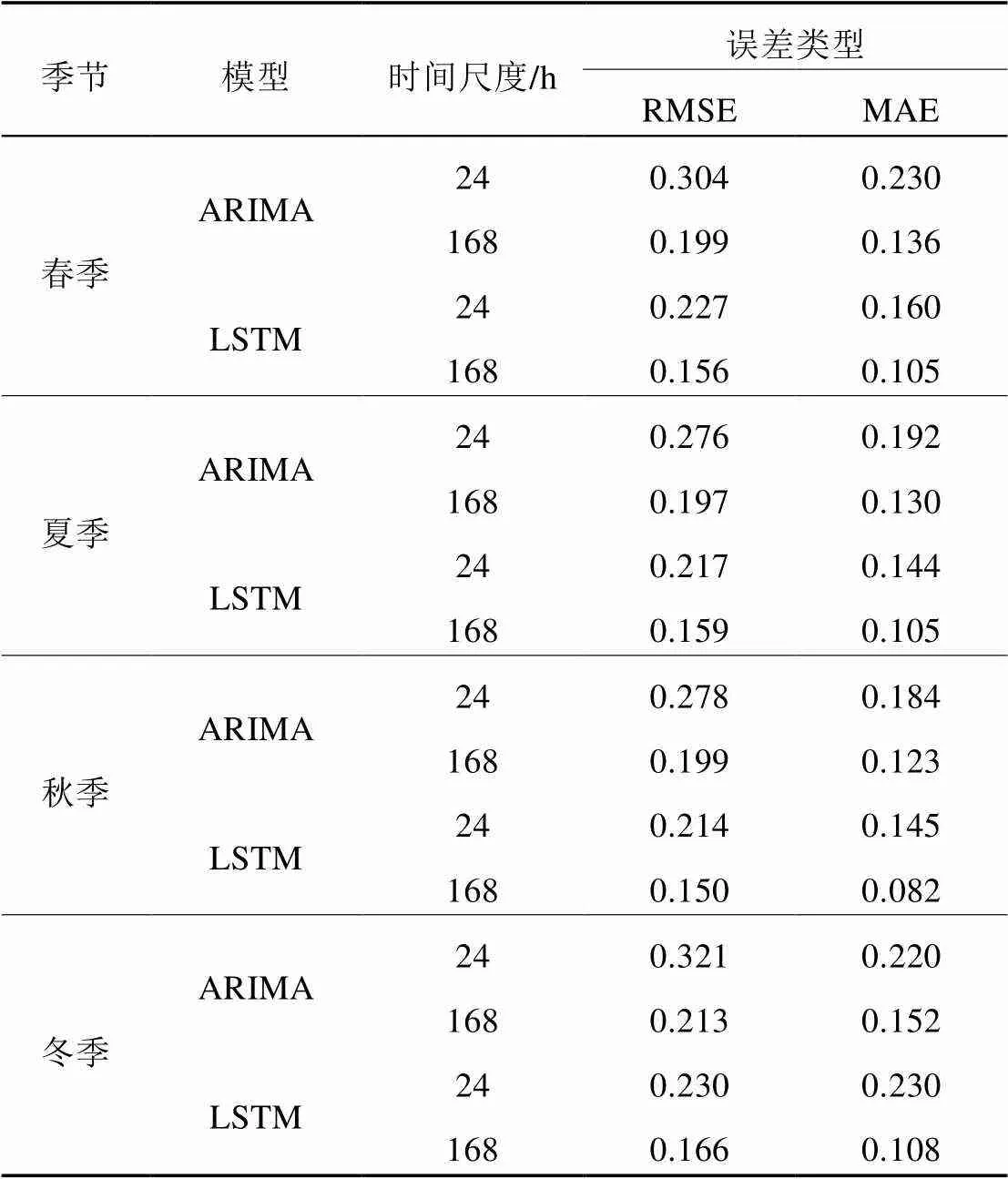
表2 基于LSTM神经网络与ARIMA算法的风力发电功率数据预测结果对比
4 结论
通过对LSTM神经网络进行分析,提出了一种基于深度学习算法的风力发电功率预测方法,以多种误差精度标准作为参考,通过与传统时序预测算法ARIMA进行对比分析得到了以下结论:
1)基于深度学习算法的风力发电功率时序预测方法可较好拟合原风力发电功率曲线,验证了该方法的有效性;
2)通过与传统ARIMA时序预测算法进行对比分析可知,LSTM神经网络的预测误差相对更小,整体效果优于ARIMA方法;
3)通过对典型四季日风力发电功率与周风力发电功率的预测分析可知,在数据规模明显提升的情况下,LSTM神经网络的预测效果优于ARIMA算法。
然而,若风力发电功率发生连续突变时,深度学习算法的跟踪变化能力有待进一步完善。下一步的研究中将融合多种优化算法,以提升深度学习算法的预测性能。
[1] 陈国初,公维祥,冯兆红.熵判别人工蜂群算法优化的风电功率[J].电力系统及其自动化学报,2017,29(7):41-45,67.
[2] 国家能源局.2018年风电并网运行情况[EB/ OL].[2019-01-28].http://www.nea.gov.cn/2019-01/28/c_137780779.htm.
[3] 周云,严正,李乃湖,等.BESS平抑风功率波动算法中多重SOC反馈策略设计[J].太阳能学报,2017,38(6):1459-1467.
[4] 薛禹胜,郁琛,赵俊华,等.关于短期及超短期风电功率预测的评述[J].电力系统自动化,2015,39(6):141-151.
[5] 闫鹤鸣,李相俊,麻秀范,等.基于超短期风电预测功率的储能系统跟踪风电计划出力控制方法[J].电网技术,2015,39(2):433-439.
[6] Liu C Y,Chao Q,Wei L L.Wind-storage coupling based on actual data and fuzzy control in multiple time scales for real-time rolling smoothing of fluctuation [J].Electric Power Automation Equipment,2015,35(2):35-41.
[7] Fang S,Chiang H D.A high-accuracy wind power forecasting model[J].IEEE Transactions on Power Systems,2017,32(2):1589-1590.
[8] Qian Z,Pei Y,Cao L X,et al.Review of wind power forecasting method[J].High Voltage Engineering,2016, 42(4):1047-1060.
[9] Hu M Y,Hu Z J,Zhang M L,et al.Research on wind power forecasting method based on improved AdaBoost.RT and KELM algorithm[J].Power System Technology,2017,37(2):536-542.
[10] 张俊,贺旭,陆春良,等.基于数值天气预报的光伏功率短期预测分类组合算法[J].广东电力,2019,32(6):55-60.
[11] 杨正瓴,刘仍祥,李真真.基于季风和大气压分布的我国风电功率预测研究[J].分布式能源,2018,3(2):29-38.
[12] 吴宇杭,温步瀛,江岳文,等.基于变分模式分解和深度门控循环网络的风速短期预测模型[J].电网与清洁能源,2018,34(12):59-64.
[13] 雷爽,王鹏卉,张亚刚.基于集合经验模态分解的组合风速预测方法[J].电力科学与工程,2018,34(1):18-23.
[14] 杨明莉,刘三明,王致杰,等.卡尔曼小波神经网络风速预测[J].电力系统及其自动化学报,2015(12):42-46.
[15] 方必武,刘涤尘,王波,等.基于小波变换和改进萤火虫算法优化 LSSVM 的短期风速预测[J].电力系统保护与控制,2016(8):37-43.
[16] 李国庆,张钰,张明江,等.基于 MRMR 的集合经验模态分解和支持向量机的风电功率实时预测[J].东北电力大学学报,2017,37(2):39-44.
[17] 曹俊波,周任军,邓学华,等.考虑优化 ARIMA 模型差分次数的风功率预测[J].电力系统及其自动化学报,2019,31(1):105-111.
[18] 李彬,彭曙蓉,彭君哲,等.基于深度学习分位数回归模型的风电功率概率密度预测[J].电力自动化设备,2018,38(9):15-20.
[19] 江岳春,张丙江,邢方方,等.基于混沌时间序列 GA-VNN 模型的超短期风功率多步预测[J].电网技术,2015,39(8):2160-2166.
[20] 陈宁,薛禹胜,丁杰,等.利用空间相关性的超短期风速预测[J].电力系统自动化,2017(12):124-130.
[21] 陈杰,沈艳霞,陆欣,等.一种风电功率概率区间多目标智能优化预测方法[J].电网技术,2016,40(8):2281-2287.
[22] 吴晓刚,孙荣富,乔颖,等.基于风电场功率特性的风电预测误差分布估计[J].电网技术,2017,41(6):1802-1807.
[23] Li D,Ren Z Y,Yan W,et al.Month-ahead wind power curve probabilistic prediction based on factor analysis and quantile regression neural network[J].Proceedings of the CSEE,2017,37(18):5238-5248.
[24] 董伟,杨强,葛磊蛟,等.基于混合智能模型的分布式风力发电预测方法[J].供用电,2019(1):34-39.
[25] Li Y,Li X J,Jia X C,et al.Monitoring and control for hundreds megawatt scale battery energy storage station based on multi-agent:methodology and system design[C]//2018 IEEE International Conference of Safety Produce Informatization.Chongqing,China:IEEE,2018.
[26] Li X J,Wang S X.A review on energy management,operation control and application methods for grid battery energy storage systems[J].CSEE Journal of Power and Energy Systems,DOI:10.17775/CSEEJPES,2019.00160.
[27] 冯泽磊,吴美凤.基于大数据平台的火电机组实时运行状态监测[J].华电技术,2019,41(4):29-32,37.
[28] 李冰,张妍,刘石.基于LSTM的短期风速预测研究[J].计算机仿真,2018,35(11):456-461.
[29] 梁荣,王洪涛,吴奎华,等.基于神经网络和 ARIMA 模型的冷热电短期负荷预测[J].电力系统及其自动化学报,DOI:10.19635/j.cnki.csu-epsa.000260.
[30] 赫卫国,郝向军,郭雅娟,等.基于ARIMA和SVR的光伏电站超短期功率预测[J].广东电力,2017,30(8):32-37.
[31] 王旭,陈潇一.基于AHP、ARIMA算法的电力信息系统负载预测研究与应用[J].电网与清洁能源,2017,33(8):20-25.
Wind Power Prediction Method Based on Long Short-term Memory Neural Network
LI Xiangjun, XU Gejian
(State Key Laboratory of Control and Operation of Renewable Energy and Storage Systems (China Electric Power Research Institute), Haidian District, Beijing 100192, China)
Wind power generation process has strong randomness, which leads to low accuracy of wind power prediction. In view of the above phenomenon,a wind power generation power prediction method based on deep learning algorithm was proposed. Taking the historical wind power data as input, a wind power prediction model was established to realize the wind power prediction on a time scale in the future. The results of the example show that compared with the traditional time-series prediction method, the average absolute error of the wind power prediction results based on long short-term memory neural network is smaller in each index, which verifies the feasibility and effectiveness of the above method in wind power generation prediction, and improves the accuracy of wind power generation prediction.
deep learning; time-series prediction; wind
10.12096/j.2096-4528.pgt.19108
国家电网公司科技项目(DG71-19-015)。
Project Supported by Science and Technology Project of State Grid Corporation of China (DG71-19-015).power generation; long short-term memory (LSTM) neural network
2019-07-16。
李相俊(1979),男,博士,教授级高级工程师,研究方向为大规模储能技术、新能源与分布式发电、电力系统运行与控制,li_xiangjun@126.com。

李相俊
(责任编辑 尚彩娟)

