装配式PC构件车辆调度问题研究

(西安建筑科技大学 土木工程学院，西安 710055)

引言

现阶段，装配式建筑在美国、英国、日本等国家的发展已经比较成熟，基本实现了在保证工程项目质量的前提下达到降低成本的目标，实现了建筑工业化。而建筑业作为我国的国民经济支柱产业，近年来保持着稳定的增长趋势。传统的现浇建筑的建造形式在施工工程中产生的资源浪费、环境污染等问题十分严重[1]，装配式建筑具有建造速度快、节省人工和材料等优点，成为近年来国家大力推广的一种新的建造形式。

由于装配式建筑在我国的发展时间不长，建造形式与传统现浇建筑存在区别，在实施过程中出现了很多困难。其中突出问题表现在装配式建筑的建造成本高于传统现浇建筑的建造成本，为了控制这一问题，很多研究者根据装配式建筑和现浇建筑建造过程进行了对比比较。李颖[2]、武长青[3]、王雪艳等[4]人得出了各分项工程中土建工程极大的增加了装配式建筑的建造成本，其它各分项工程较高于或者低于现浇建筑相应成本，而土建工程中PC构件的成本远大于现浇构件的成本，因此对装配式PC构件的增量成本进行分析后得出如图1所示。

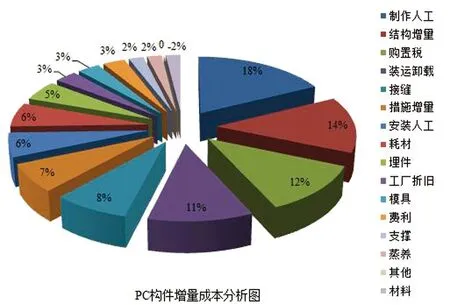
图1 装配式PC构件增量成本分析图(来源：地产成本圈)

从图1可以看出，PC构件成本构成包括人工、材料、运输、措施费、养护等，其中除材料费用为减量成本以外其它费用均为增量成本，且制作人工、结构增量、购置税和装运卸存增加均超过10%，因此得出装配式PC构件运输成本是影响装配式PC构件价格的主要因素之一[5]。许多学者针对装配式建造过程或者PC构件生产过程进行了相关成本控制方面的研究，潘寒等[6]人对PC构件工厂排产，缩短了构件的加工时间，但是对于PC构件的运输成本研究少之又少，因此在研究装配式PC构件运输特点、传统车辆调度以及相关求解算法后建立了PC构件运输成本模型。

1 装配式PC构件运输成本分析

1.1 车辆调度问题

车辆调度是指在车辆满足一定的约束条件下，通过制定行车路线，完成运输任务后达到配送距离最短、油耗最少、费用最低等一系列的目标。研究后发现，车辆调度问题是典型的复杂组合优化问题[7]。传统车辆调度问题中涉及的因素主要有配送中心、货物接收点、车辆选择、运输距离、车辆运输要求和完成运输任务的目标。蔡宁等[8]人使用BIM技术和MHEFT算法优化某工程的施工进度计划。

车辆调度问题的特点主要是：车辆从配送中心出发最后返回配送中心； 车辆的载重量远远大于一个货物接收点的重量； 车辆的固定成本远大于其可变成本等。针对装配式PC构件体量大、对时间要求严格等特点，得出装配式PC构件的车辆调度的特点主要是：车辆从预制构件厂出发最后返回预制构件厂； 车辆需要多次运输预制构件到一个施工工地完成需求量要求； 车辆的型号对预制构件的成本影响较大等。

1.2 装配式PC构件运输模型

根据装配式预制构件的主要特点，从配送车辆进行调度的实际情况出发，结合施工现场预制构件需求量确定不同车型的空载单位油耗、满载单位油耗、单位油耗价格、距离等确定的条件下建立了由车辆固定租赁、人工成本和油耗成本构成的单一预制构件厂运输预制构件到多个施工工地的综合成本最优的运输成本模型。结合相关参考文献和装配式PC构件的特点，本文对PC构件运输成本模型进行下列假设：

1)车辆在行驶过程中保持匀速且没有出现交通堵塞等不良情况；

2)车辆油耗只与其载重量、运输距离有关，且成正比例关系；

3)配送前PC构件已经装车完毕，且车辆到达每个施工工地后直接卸货，不需要等待；

4)预制构件厂的PC构件库存量满足各施工工地的要求；

5)运输车辆从预制构件厂出发到达施工工地后，必须返回预制构件厂，完成一个过程运输任务；

6)运输车辆行驶的各施工工地的运输路线是确定的，即运输距离固定；

7)运输车辆一天内运输预制构件到达施工工地的次数确定；

8)车辆一旦开始运输任务，不得退出。

装配式PC构件运输成本模型表示如下：

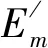
(1)

其中，INT是将一个数值向下取整为最接近的整数的函数，为取整函数。

一种车型m完成施工工地z需求量的总次数为用公式2表示：

(2)

当B∈INT，运输车型m载重到施工工地z时的实载率用公式3表示：

(3)

当B∉INT，运输车型m载重到施工工地z时的实载率用公式4表示：

(4)

车型m载重时的单位距离油耗用公式5表示：

(5)

定义决策变量：

根据上面的参数和变量建立的成本数学模型如公式6所示：

(6)

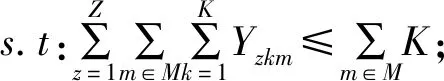
(7)

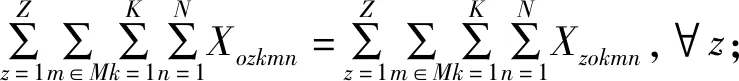
(8)

(9)

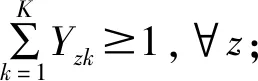
(10)

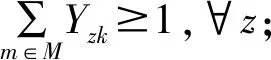
(11)

其中，式(6)表示运输车辆的油耗成本和固定成本最优的目标函数； 式(7)表示运输预制构件的车辆的总数目不能超过预制构件厂所租赁的车辆数； 式(8)表示确保运输车辆从预制构件厂出发并返回到预制构件厂； 式(9)表示到达一个施工工地的车辆次数满足施工工地的需求量； 式(10)表示保证每个施工工地都被服务； 式(11)表示到达施工工地的车型至少一种。

1.3 改进粒子群算法

启发式算法是指导算法在可解空间中寻找较好解但并不能保证每次都能找到更好解，更不能保证得到最优解的一种算法，其中粒子群算法是启发式算法的一种[9]。常媛等人[10]对遗传算法、启发式算法进行了相关研究，综合考虑本文采用粒子群算法。

粒子群算法主要源于对鸟群的研究，优点是概念简单、容易实现且在运行过程中需要调节的参数较少，缺点是收敛速度快，主要通过速度向量和位置向量更新粒子的状态[11]。传统的粒子群算法是用于解决连续性优化问题的，但是随着应用领域的不断扩大，连续性的粒子群算法已经无法满足很多实际问题的求解，例如PC构件车辆调度问题。通过查阅相关文献和对装配式PC构件特点进行分析，对传统粒子群算法做了惯性权重和编码方式方面的改进。

(1)惯性权重的改进

参数ω能够针对不同的搜索问题，进行适当的调整，能够达到平衡局部和全局区域最优搜索的能力，因此ω的取值至关重要，黄洋[12]、Shi和Eberhart[13]等人对惯性权重进行了相关研究，Shi和Eberhart通过实验得出的结论，综合分析后将惯性权重定义为一个随着时间推移不断减少的线性函数，目的是使粒子在刚开始的时候能够不断的搜索新的区域，随着时间的推移，惯性权重减小，粒子趋向于在局部范围内搜索最优解，并快速汇聚在一起，经过不断的迭代后得到全局最优解。惯性权重的函数形式如公式12进行表示：

(12)

其中，ω1表示初始权重ω2表示最终权重，Q表示迭代次数，Q1表示当前迭代次数。

(2)编码方式的改进

最初的粒子群算法采用实数的编码方式求解连续问题，为了发挥粒子群算法本身的优点，胡小宇等[14]人提出了基于后继的排位编码方式，吴斌[15]提出了实数向量的编码方式，根据PC构件配送特点，本文采用实数向量的编码方式，将实数中整数与小数分别赋予不同的定义。整数表示车辆数，小数的范围表示车辆型号，在同一区间内的小数大小表示车辆行驶的顺序。

2 算例求解

2.1 算例描述

某地区有一个装配式PC构件预制工厂，主要生产的预制构件有预制内外墙、预制板、预制楼梯、预制空调板、预制阳台板、预制梁和预制柱。现已知该预制构件厂需要运输预制构件到周围四个施工工地，关于施工工地距离预制构件厂的距离、一天内预制构件需求量等信息如表1所示。在车辆选择方面，预制构件厂有三种车型可供选择，车型相关参数信息如表2所示，已知车辆一天内达到施工工地的次数为4次。

2.2 精确算法求解

精确算法也称为最优化算法，主要是通过分析后建立具体问题的数学模型，然后根据数学模型利用归纳法、综合法等数学方法进行模型求解，得到问题的最优解。根据表1和表2计算得到满足施工工地预制构件需求量的前提下，运输到施工工地车辆最少时不同类型车辆运输次数的排列组合。表3为满足施工工地1需求量的优化组合。

表1 预制构件厂到施工工地的距离和需求量信息

施工工地预制构件厂到施工工地的距离(km)预制构件的需求量(件)预制构件的单件重量(t)110预制墙602.6214叠合板553.0313预制阳台板661.8412预制墙622.3

表2 不同车型的车辆性能参数

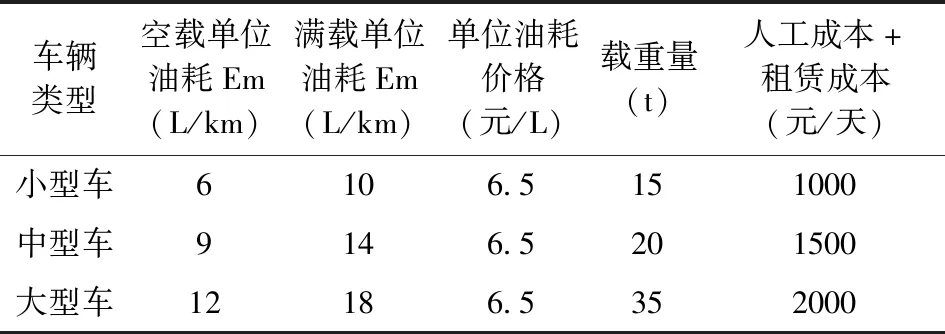
车辆类型空载单位油耗Em(L/km)满载单位油耗Em(L/km)单位油耗价格(元/L)载重量(t)人工成本+租赁成本(元/天)小型车6106.5151000中型车9146.5201500大型车12186.5352000

表3 满足施工工地1需求量的优化组合

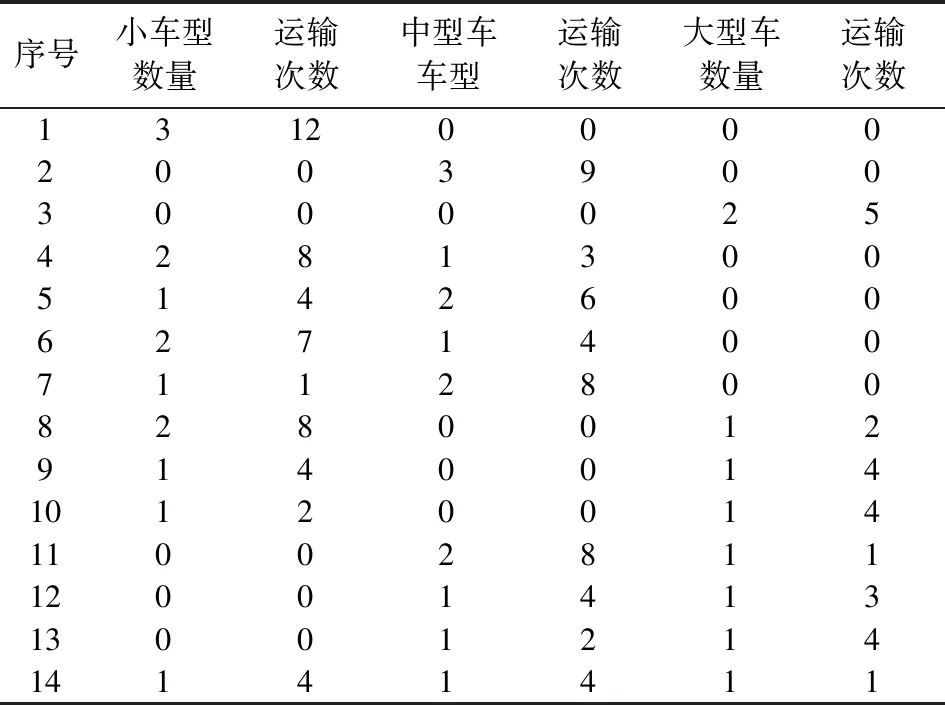
序号小车型数量运输次数中型车车型运输次数大型车数量运输次数13120000200390030000254281300514260062714007112800828001291400141012001411002811120014131300121414141411

依次求解得出不同施工工地的优化组合，将满足四个施工工地需求量的车型和车辆次数的可行域为各施工工地的排列组合，有14*14*10*12=23520种可能性。使用综合成本目标函数结合表2给出的车辆成本相关参数，求解得到的最优成本为54083元。得到最优成本车辆配送方式如表4所示。

表4 最优成本车辆配送方式

第一次配送第二次配送第三次配送第四次配送1号大型车施工工地1施工工地1施工工地1施工工地12号大型车施工工地2施工工地2施工工地2施工工地23号大型车施工工地3施工工地3施工工地3施工工地34号大型车施工工地1施工工地2施工工地4施工工地41号中型车施工工地4施工工地4施工工地4施工工地4

结合案例提供的相关信息，通过精确算法的计算，得出了预制构件厂运输预制构件综合成本最低的车型和车辆数量的选择，同时解决了关于车辆如何配送的问题。在精确算法的求解过程中发现，运输车辆组合优化选择不合理将大大影响运输费用，合理的车辆调度方案是至关重要的。

尽管精确算法能够得到最优解，但是随着车型性能参数和施工工地数量等的增多，解的排列组合也呈指数增长，得到结果需要花费大量的时间和精力，因此对于涉及参数较多的车辆调度问题一般不采用精确求解的方法。本文使用精确算法结果与改进粒子群优化算法结果进行比较，达到验证改进粒子群优化算法正确性的目的。

2.3 改进粒子群算法求解

改进的粒子群优化算法采用JAVA语言编写，将相关信息输入到编写完成的改进粒子群优化算法中，算法涉及的相关参数设置为：种群数量为50，惯性权重ω1为1.2，惯性权重ω2为0.4，加速因子为1.4，rand()为0-1之间的随机数，迭代次数Q为500。本案例施工工地为4个，车型为三种，在车辆数未知的前提下，采用实数向量的编码方式，将大型车小数限制为0.01-0.33之间，中型车小数限制为0.34-0.66，小型车小数限制为0.67-0.99。

经过计算后得到了最优解的分组结果和车辆调度的配送方案。从车辆调度方案可以看出预制构件厂运输预制构件时需要租赁的车型、车辆数量，同时如何分配车辆运输到施工工地。完成本案例项目，预制构件厂租赁大型车4辆，中型车1辆。其中大型车的第一辆车运输PC构件到达施工工地1四次，中型车的第一辆车运输PC构件到达施工工地4四次，大型车的第二辆车运输PC构件到达施工工地2四次，大型车的第三辆车运输PC构件到达施工工地3四次，大型车的第四辆车运输PC构件到达施工工地4两次，到达施工工地1一次，到达施工工地2一次，完成配送任务。

将改进粒子群优化算法的运算结果和车辆调度方案与精确算法求解的结果进行分析后的得出，改进粒子群优化算法能多次找到最优解，证明了改进粒子群算法的正确性。改进粒子群优化算法帮助预制构件厂在选择租赁车型和车辆数量的问题以及车辆如何分配的问题上提供了有效的方法。

3 总结

装配式PC构件运输成本是影响PC构件成本构成的主要因素之一，是控制成本的重点分析对象。通过分析车辆调度、粒子群算法等相关内容，建立了装配式PC构件运输成本模型，并通过案例进行验证了改进粒子群优化算法的正确性和有效性。同时实现了多车型问题下求解PC构件运输成本最优的车辆调度方案，解决了PC构件运输成本中对不确定车型和车辆数的选择空白。