基于统计试验设计下花岗岩两种本构模型研究

温燕华，袁周祥，薛少欣

(河北工程大学 水利水电学院，河北 邯郸 056038)

0 引 言

岩石材料的细观本构特征，决定了岩石材料的宏观力学行为特征。基于颗粒流理论的PFC(Particle Flow Code，PFC)软件可以将细观力学参数与宏观力学参数联系起来，用以模拟岩石的基本力学特性。该方法是P. A. Cundall等在离散元理论基础上提出的，将颗粒的运动以及颗粒间应力的交互作用作为模拟岩石的基本条件[1]。目前，颗粒流程序中用于表征岩石材料细观本构的两种主流模型分别为平行黏结模型(Parallel-Bonded，PB)和平直节理模型(Flat-joint，FJ)。平行黏结模型由POTYONDY等[1-2]创建，针对该模型在模拟岩石力学特性的理论方法以及优势方面进行过详细阐述；而蒋明镜等[3]在研究中发现，平行黏结模型虽然可以较为准确的模拟岩石的脆性破坏特征，但是计算得出的单轴抗拉强度较高，与实际结果存在差异。后续，POTYONDY[4]建立Flat-Joint接触模型，通过构造颗粒形状及新的接触本构关系，使颗粒破坏后的旋转遭到抑制，显著提升了材料的压拉比(USC/TS)，但未指出Flat-Joint接触模型的适用范围以及缺陷。刘富有等[5]、陈鹏宇等[6]则针对Flat-Joint模型，研究宏细观参数间的对应关系，并建立了相应的标定方法，但并未对模型的计算稳定性、破坏特性等方面进行阐述。

尽管上述研究贡献诸多成果，但仍有待于进行补充与完善。众所周知，基于颗粒流方法生成岩石材料时，颗粒半径大小是按均匀分布生成，颗粒间的黏结强度是按正态分布生成。这两种随机因素均会对模型的宏观力学参数与破坏特征存在显著影响，即影响计算结果的稳定性。基于此，本文以新疆奇热哈塔尔过水隧洞片麻状花岗岩力学参数为基础，建立二维离散元模型，通过统计学的试验方法，对比分析PB模型与FJ模型在宏观力学参数及破坏模式的差异性与稳定性，为后续改进本构模型以及选取合适的本构模型进行岩石数值模拟提供理论依据。

1 研究方法

1.1 物理实验

以新疆齐热哈塔尔过水隧洞的片麻状花岗岩为研究对象，采用TAW-2000微机控制电液伺服岩石三轴试验机对岩石试块进行单轴压缩试验，加载速率0.002 mm/s，得到岩石的物理力学参数以及破坏模式。见图1。

图1 试验示意图以及岩石破坏模式Fig.1 Test schematic diagram and the rock failure mode

宏观物理力学参数见表1，以单轴抗压强度、弹性模量、泊松比、抗拉强度作为细观参数反演的主要目标值。

表1 岩石宏观力学参数Tab.1 Macroscopic mechanical parameters of rock

1.2 模型的建立及计算

本试验是在颗粒离散元PFC2D软件平台上完成。单轴抗压模型尺寸为长100 mm、宽50 mm。颗粒平均半径为0.3 mm，最大半径与最小半径比值为1.66。通过半径扩大法来调整模型内的颗粒分布，颗粒半径在最大半径与最小半径之间服从均匀随机分布。巴西劈裂数值模型半径为25 mm，颗粒半径设置与单轴压缩相同。利用内嵌Fish语言编写伺服算法控制加载墙体运动，加载速度设置0.02 mm/s，以此实现单轴以及巴西劈裂的数值模拟试验。

1.3 参数的选取

岩石宏观力学参数与细观力学参数之间存在高度非线性关系，两者之间的函数关系无法用精确的数学表达式表示。因此需通过数值力学试验，进行宏细观匹配演算。本文针对上述两种细观本构，开展单轴压缩试验和巴西劈裂试验，单轴试验获取的宏观力学参数包括弹性模量、抗压强度、泊松比，巴西劈裂试验获取的宏观力学参数为抗拉强度。当该细观本构的数值模拟结果与目标值的相对误差在5%以内，则以该组细观参数为基准研究该细观本构数值计算结果的稳定性。需要说明的是，由于PB模型无法准确计算出抗拉强度，因此在宏细观匹配演算过程中不考虑该力学参数。根据上述方案，细观参数的计算结果见表2，由表2中的细观参数列表可知，FJ本构比PB本构多出一个接触片段参数。

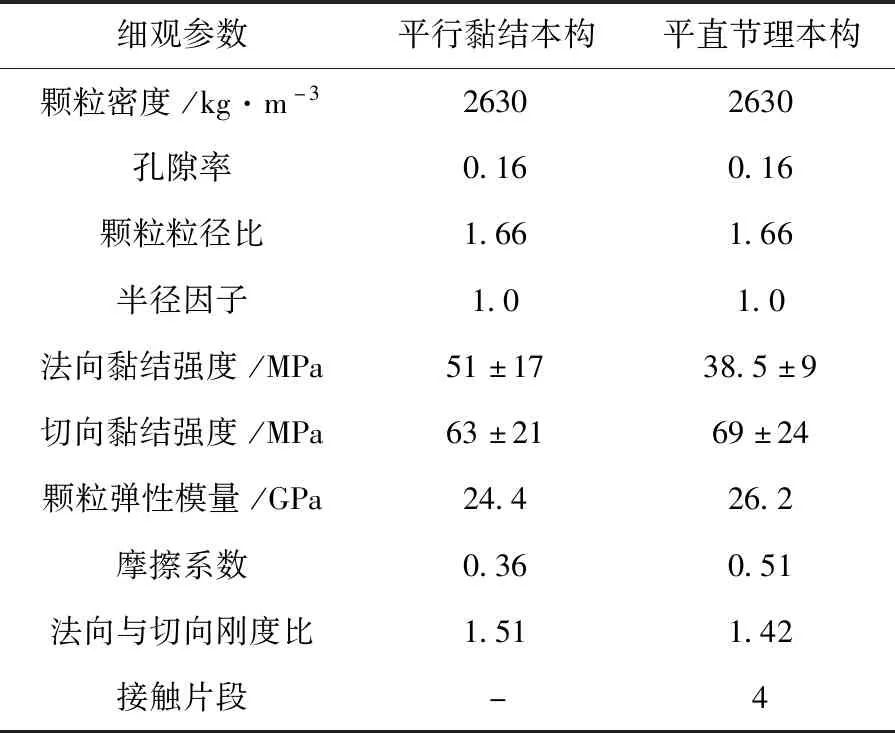
表2 两种本构模型细观参数Tab.2 Mesoscopic Model Mesoscopic Parameters

1.4 试验方案

依据研究目的，针对PB本构与FJ本构各随机生成10组用于单轴压缩试验的试样以及10组用于巴西劈裂试验的试样。随机因子分别设置为1001，2001，3001，4001，5001，6001，7001，8001，9001，10001。

由此可知，数值试验结果数据为成组设计定量资料，区组因素为细观本构。本文将采用描述性统计方法，针对两种本构模型，计算分析其宏观力学参数的稳定性以及破坏特征。采用定量统计检验的方法，针对两种本构模型，检验其宏观力学参数的统计学差异性。选用统计检验方法的原则如下：若各组数据资料满足独立性、正态性与方差齐性，则优先选用检验功效较高的参数检验——T检验，否则采用相应的非参检验——Wilcoxon秩和检验[7]。根据文献[8-11]的建议，利用Shapiro-Wilk检验和Levene检验对资料的正态性和方差齐性进行检验。

2 试验结果及分析

2.1 宏观力学参数的稳定性分析

如试验方案所述，通过力学试验，获取两种细观本构的宏观力学参数，采用描述性的统计方法进行分析。图2展示的是抗压强度、弹性模量、泊松比以及压拉比的数值试验结果。由图2中数据可知，两种细观本构的抗压强度、弹性模量、泊松比的均值数据相差较小，并未体现出较大的数值差异；而压拉比的均值则表现出较大的数值差异，即FJ模型的压拉比均值要远大于PB均值。同时，由各样本数据分布特征、标准差(Standard Deviation，SD)以及变异系数(Coefficient of variation, CV)可看出，FJ模型的各力学参数的离散程度均大于PB模型。FJ模型除了弹性模量的变异系数小于5%以外，其它力学参数的变异系数均高于5%，以压拉比最为明显。PB模型除了压拉比的变异系数略大于5%以外，其它力学参数的变异系数均低于5%。

以上研究结果说明，两种本构模型对力学参数的均值影响很小，即均能体现出花岗岩的宏观力学特性。二者主要区别在于力学计算结果的稳定性方面，PB模型的力学计算稳定性质明显优于FJ模型；但是由于无法准确标定抗拉强度，在模拟岩石的真实压拉比方面，FJ模型要优于PB模型。

图2 花岗岩数值模型力学参数结果Fig.2 Results of mechanical parameters of granite numerical model

2.2 宏观力学参数的统计检验分析

由表3可知，两种细观本构模型的抗压强度、弹性模量、泊松比的样本数据均满足正态性与方差齐性，因此可以采用T检验来比较两组样本均值是否存在显著的统计学差异。本文将显著性检验水平定为0.05，假设检验为两组样本的总体均值相等。由统计检验结果可知，这3类宏观力学参数的均值，在两种本构模型之间并未存在显著的统计学差异，即两种细观本构在描述同一种岩石材料时，在抗压强度、弹性模量、泊松比上具有较高的一致性。但抗拉强度均值及压拉比均值在两种本构模型之间存在显著的统计学差异，即FJ模型的压拉比远高于PB模型，前者更能客观体现出岩石材料的抗拉强度。

表3 宏观力学参数的统计分析结果Tab.3 Statistical analysis results of macroscopic mechanical parameters

2.3 破坏模式分析

图3与图4分别为FJ模型与PB模型在不同压拉比下对应的破坏模式图。由图3可知，PB模型所表现的破坏模式以单斜面剪切滑移为主，同时在剪切带附近形成多条次生裂纹带。次生裂纹带方向趋向于加载应力方向，这说明次生裂纹带多为试件横向膨胀所形成的张拉破坏。由图4可知，FJ模型表现的破坏模式主要表现为两种：①单斜面剪切破坏；②随着压拉比的增加，剪切带与试件轴向夹角逐渐减小，呈现为轴向劈裂以及表层剥离的破坏模式，即这些破坏主要是由于横向拉应力超过岩石抗拉极限所引起的。

图3 不同压拉比下，PB模型的主要破坏模式Fig.3 Main failure modes of PB model under different draw ratios

图4 不同压拉比下，FJ模型的主要破坏模式Fig.4 Main failure modes of FJ model under different draw ratios

将黏结键断裂倾角按10°间隔进行分组，统计每组倾角范围内的断裂数占总裂纹数的比值，绘制相应的裂纹倾角玫瑰图，见图5。由图5可看出，两种细观本构模型的破坏裂纹倾角集中在45°～145°之间，均表现出以斜剪破坏为主，但亦有拉伸破坏。倾角在90°附近的裂纹数，FJ模型要高于PB模型，由上述分析可知，这是由压拉比较高的条件下所导致。

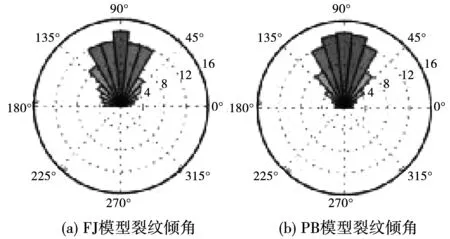
图5 不同本构模型硬岩的裂纹倾角玫瑰图Fig.5 Crack dip rose of hard rock with different constitutive model

由以上分析可知，PB模型在表现花岗岩宏观破裂模式方面较为稳定，以斜剪破坏为主，但会伴生次生的张拉裂纹，这主要是由于PB模型压拉比变化范围较小所致。FJ模型在宏观破裂模式上，会随着压拉比的变化，呈现斜剪向拉伸破坏模式的转变，即更能表现出岩石材料的非均质性。

3 结 论

以新疆奇热哈塔尔过水隧洞片麻状花岗岩物理实验力学参数为基础，建立颗粒流花岗岩数值模型，在考虑颗粒半径及细观黏结强度随机分布的条件下，通过单因素成组的试验设计，对比分析FJ本构模型与PB本构模型在宏观力学参数及破坏模式的差异性与稳定性，共得出以下结论：

1) 两种本构模型均能做到较为准确描述片麻状花岗岩材料宏观力学参数，如弹性模量、抗压强度、泊松比，但PB模型力学参数的变异系数均低于FJ模型，即从计算稳定性角度来讲，PB模型计算结果更具有确定性。

2) PB模型由于自身理论的缺陷，相对于FJ模型未能表现出花岗岩岩石材料真实的压拉比这一力学性质。因此，利用PB模型研究均质性较强且抗拉强度较高的硬岩材料的力学行为时，更容易发现普遍性规律，具有一定优势；而对于均质性较弱且压拉比较高的硬岩材料，FJ模型更为适合。

3) 两种细观本构模型的破坏裂纹倾角集中在45°～145°之间。PB模型在单轴压缩状态下，其花岗岩材料的宏观破坏模式以斜剪破坏为主，在宏观裂纹带两侧会伴生次生的张拉裂纹，破坏模式相对稳定，这主要由压拉比及PB模型计算稳定性所决定。FJ模型在宏观破裂模式上，会随着压拉比的变化，呈现斜剪向拉伸破坏模式的转变，张拉裂纹数要高于PB模型，其宏观破坏模式较为不确定，更能表现出岩石材料的非均质性。

4) 针对以上研究结果，建议今后在进行花岗岩等硬性岩石材料的数值试验时，可根据研究内容与岩石特性，选择合适的本构模型，为后续研究岩石破坏机理提供参考价值。