应用分块三次多项式的导引头测角精度标定

袁东明，丁亚林，张健,3

(1.中国科学院 长春光学精密机械与物理研究所, 吉林 长春 130033; 2.中国科学院大学, 北京 100049;3.中国科学院 长春光学精密机械与物理研究所 航空光学成像与测量中国科学院重点实验室，吉林 长春 130033)

0 引言

导引头是精确制导系统不可或缺的组成部分，主要功能是完成对目标的搜索、捕获、跟踪与测量[1-2]，作为光电探测系统从应用波段上可分为可见光导引头、红外导引头、激光导引头等；从结构形式上可分为框架式、捷联式。近年来，激光制导武器以其精度高、威力大、抗干扰能力强等优点成为现代精确打击的重要手段之一[3-4]。

在整机系统工作过程中，激光导引头负责测量载体视线角，其精度高低直接影响控制系统的稳定性与制导精度，而影响测角精度的主要因素有机械零件加工、装配误差，光学零件加工、装配误差，探测器及后续信号处理电路引起的电学系统误差，除此外，还包括在工作过程中由振动、温度以及电学系统噪声引起的随机误差。从这些因素出发，如何进一步提高导引头测角精度，俨然是一个需要特别关注的问题。过度地提高光机系统加工、装调精度，提高探测器等光电元器件指标，会造成生产周期、成本的大幅上升；与此同时，上述精度指标对于现有技术来说也不切实际。相比之下，通过系统标定的方法提高导引头精度方便灵活，更具可行性[5-6]。正确的标定方法往往能突破设计极限，使得系统精度获得数量级的提升。目前对系统的标定从原理上可以分为基于参数模型的标定方法和基于非参数模型的标定方法[7-8]。参数模型标定方法基于精确的数学模型，而非参数模型标定方法可规避数学模型建立的困难，但需要一定量的观测数据。

Huang等[9]全面分析了某光电望远镜指向精度的误差因素，并以此建立了运动模型，然后进行线性化，忽略2阶及以上小量，最后通过偏最小二乘法进行参数识别，得到了较好的结果，该方法除忽略次要因素的影响外，过程也较为复杂。孙辉等[10]分析了影响导引头指向精度的误差项，建立了系统运动学方程并对其线性化，提出分步最小二乘法，实现了指向误差的标定。该方法具有较好的标定效果，然而其研究对象为线性光电探测器，并不适合本文的四象限探测器。赵明等[11-12]和朱明超等[13]采用局部指数积及最小二乘优化找出最优系统识别参数，但由于初始姿态误差与关节变量误差不能统一到误差模型中进行辨识，从而限制了该方法的标定精度。陈勇等[14]推导出四象限探测器测量的实际偏移量和传统算法计算偏移量之间的关系，对探测器的非均匀性进行了定量补偿。该方法很好地消除了探测器误差，但未考虑导引头系统其他误差的影响。此外，上述研究均未考虑随机误差对标定的影响[15-17]。

本文采用分块三次多项式对某激光捷联导引头测角误差进行标定，规避了因四象限探测器系统误差存在隐式非线性[14]而造成建模困难的问题，考虑了随机误差对系统误差标定的影响[15，17]，同时保证标定实验数据节点1阶导数、2阶导数的连续性[16]，以提高标定精度。首先，分析影响导引头测角精度的各项误差及特点；其次，给出分块三次多项式标定方法的数学原理；最后，搭建实验测试系统，对所提方法进行验证。实验结果表明：该方法稳定、可靠，具有较高精度，完全满足导引头研制需求，对此类工程问题提供了参考。

1 导引头模型及误差分析

1.1 导引头几何模型与坐标系

图1 导引头结构示意图Fig.1 Schematic diagram of seeker structure

本文所研究导引头安装在导弹头部。为了避免框架式导引头中陀螺、编码器及相应轴系引入的误差，本系统采用捷联式导引头。具体结构如图1所示，图中Oxbybzb、Oxlylzl、Oxgygzg、Oxdydzd表示理想坐标系。

由图1可知，该导引头系统由弹体、镜筒、光学系统(含球罩)、四象限探测器及信号处理板等组成。光学系统安装在镜筒内，位置通过光学表面与机械表面配合及内部隔圈、压圈固定；四象限探测器通过自身定位面与定位孔固定在镜筒上；镜筒通过法兰与弹体柱面配合，另加定位销周向定位后固连于弹体上。

为了更好地说明该导引头测角误差来源，在光学中心处建立了4个坐标系(见图1)：

1)弹体坐标系Oxbybzb. 该坐标系与弹体固连；坐标原点位于光学中心；Oxb轴同飞行方向；Ozb轴竖直向上；Oyb轴由右手定则确定。

2)镜筒坐标系Oxlylzl. 该坐标系与镜筒固连；Oxl轴为镜筒法兰与弹体配合柱面轴线，方向同飞行方向；Ozl轴位于镜筒纵向对称面内与Oxl轴垂直，方向竖直朝上；Oyl轴由右手定则确定。

3)光学坐标系Oxgygzg. 该坐标系与光学镜片固连；Oxg轴为光学系统光轴，方向同飞行方向；Ozg轴在光机装调理想位置下与Ozl轴相同；Oyg轴由右手定则确定。

4)探测器坐标系Oxdydzd. 该坐标系与探测器固连；Oxd轴垂直探测器靶面，方向同飞行方向；Ozd轴由探测器周向定位孔确定，理论上与Ozg轴相同；Oyd轴由右手定则确定。

上述4个坐标系，在导引头装配完毕后，位置和姿态相互固定，在理想情况下应完全重合。

1.2 导引头测角误差分析

基于1.1节的4个坐标系，可知该导引头系统测角误差来源(见图2)为：

1) 由于弹体与镜筒配合面加工误差、安装时的装调误差，造成镜筒系相对弹体系存在俯仰角误差Δθlb及偏航角误差Δγlb. 上述误差角度定义满足以下坐标转换关系：

Mlb=Ryl(Δθlb)Rzl(Δγlb)，

(1)

式中：

图2 坐标系示意Fig.2 Coordinates

2) 由于光学镜片与镜筒配合面加工误差，隔圈、压圈加工误差以及镜头装调误差，造成光学系统光轴与理想位置产生偏差，即存在俯仰角误差Δθgl及偏航角误差Δγgl. 上述误差角度定义满足以下坐标转换关系：

Mgl=Ryg(Δθgl)Rzg(Δγgl)，

(2)

式中：

3) 由于四象限探测器与镜筒配合的定位面、定位孔存在误差，使得探测器系与光学系产生滚转角误差Δαdg(四象限探测器测角原理不具有轴对称性，应计入滚转角误差)、俯仰角误差Δθdg及偏航角误差Δγdg. 上述误差角度定义满足以下坐标转换关系：

Mdg=Rxd(Δαdg)Ryd(Δθdg)Rzd(Δγdg)，

(3)

式中：

4) 探测器测角原理误差，通过文献[12]可知，四象限探测器测得光斑重心距探测器平面坐标系原点偏移值dx与实际偏移值x存在如下关系：

(4)

式中：r为重心距探测器平面坐标系原点的距离。根据上述方法测得光斑重心，结合镜头焦距可以求出目标俯仰角与偏航角。

5)信号处理板引入系统误差，由于电学元器件、PCB设计原理及加工误差等，造成输出量与实际值存在偏差。

上述均为该导引头系统误差，可以通过实验加以标定。若不考虑误差项4和5，则可以通过坐标转换建立精确数学模型，然后利用实验进行参数标定达到目的。然而，由于误差项4的隐式非线性关系，及误差项5难以用精确数学模型表达，以至建立精准数学模型较为困难。因此，本文采用分块三次多项式的非参数标定法，对该导引头测角误差进行标定。

2 分块三次多项式标定原理

分块三次多项式标定实质为二维插值，因其对被插区域分块插值，可避免整体插值的Runge现象。另外，该方法属于分块内插，即在每个分块区域拟合一个三次曲面，由于其考虑了1阶偏导数与2阶混合导数，能保证相邻分块曲面的连续与光滑[14]。

针对本文研究问题，将目标实际俯仰角θr、偏航角γr均视为测量俯仰角θm、偏航角γm的连续光滑函数，即

θr=f(θm,γm)，

(5)

γr=h(θm,γm)，

(6)

式中：f(·)、h(·)为被插函数，满足所需的连续性。该导引头光学系统及探测器测角范围为俯仰角不小于±10°、偏航角不小于±10°，工作范围为俯仰角不小于±8°、偏航角不小于±8°. 因此，取被插区域为

(7)

图3 视场范围Fig.3 Range of field of view

对(7)式被插区域离散化，间隔2°，具体如图3所示。由图3可知，标定用实验数据点有11×11个。设图中阴影区域为某一分块被插区域，其左下角点序号为(i,j)，向右i序增大，向上j序增大。则可利用分块三次多项式拟合该区域函数曲面(为表述通用性，下以X、Y、Z表示横坐标、纵坐标及函数值)：

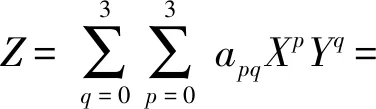
(8)

式中：X为测量俯仰角；Y为测量偏航角；Z为俯仰角真值或偏航角真值；aij为待定系数。

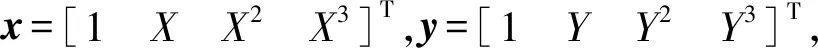
z=xTAy，

(9)

利用阴影区域及其外围，共16个实验点，可求得阴影区域4角点1阶偏导数和2阶混合导数：

(10)

式中：m=i,i+1；n=j,j+1；L=2°. 再结合其函数值，有

(11)

综上所述，根据(11)式可求得任意分块三次多项式的待定系数矩阵A. 当探测点落入某一分块区域时，根据(8)式可求得对应实际值，至此建立了探测值到实际值的映射关系。

3 标定实验与结果分析

3.1 实验方法

针对本文研究的某激光制导导引头，设计标定实验装置，实物如图4所示。

图4 导引头标定实验实物Fig.4 Experimental system for calibration

由图4可知，实验系统包括：激光发生器、调光模块、目标模拟器、二轴转台、导引头、三轴转台，另外，还包含数据采集的上位机。依照图3所示实验点、校核点进行实验，具体步骤如下：

步骤1检查三轴转台、二轴转台同轴。将导引头固定于三轴转台滚转框架上；将目标模拟器固定于二轴转台内框架(俯仰轴)上。

步骤2用光纤将激光发生器、调光模块及目标发生器连接在一起；将激光发生器线路接通；将导引头线缆与上位机连接。

步骤3给二轴转台、三轴转台上电，使目标模拟器出射光线对准导引头光轴，给上位机、导引头、激光发生器上电，确定所有设备工作正常。

步骤4按照图3所示实验点、校核点进行测试。为了减小实验过程中由于振动、温度变化、电噪声等引起的随机误差对将来系统误差标定的影响，对每一个数据点对应的实际俯仰角、偏航角测量4次后取平均值，这里测角实际真值为转台测量值。这样可以保证置信概率P=0.95时，平均值随机误差比单次测量值更小[15]。

步骤5测试完毕，保存数据。

实验共获得121组用于标定的数据和64组用于校核的数据，具体数值如表1、表2所示。

3.2 标定与结果

根据分块三次多项式标定方法及实验获得用于标定的121组数据。将工作区域分为64块，对每一块区域分别建立由测量俯仰角、偏航角到实际俯仰角或偏航角的映射关系。

根据上述映射关系，将校核点俯仰角、偏航角分别代入对应区域关系式中，得到标定后的俯仰角与偏航角θc、γc. 记原测量俯仰角、偏航角误差为Δθo=θm-θr、Δγo=γm-γr；标定后俯角、偏航角误差为Δθn=θc-θr、Δγn=γc-γr.

为直观表示标定前后俯仰角、偏航角误差，分别将俯仰角、偏航角误差随测量俯仰角、偏航角的分布绘制如图5、图6所示，对上述误差进行统计后，绘制直方图如图7所示。

由图5、图6可知，标定后误差较标定前数值减小，且在导引头工作视场区域内波动小，具有良好的稳定性。由图7可知：标定后俯仰角、偏航角误差均值由原来的0.136 0°、0.336 4°降至0.004 7°、0.001 5°；最大误差由原来的0.761 1°、0.992 0°降至0.076 1°、0.057 1°；方差由原来的0.382 0°、0.375 2°降至0.026 9°、0.022 7°.

表1 标定点实验数据

表2 校核点实验数据

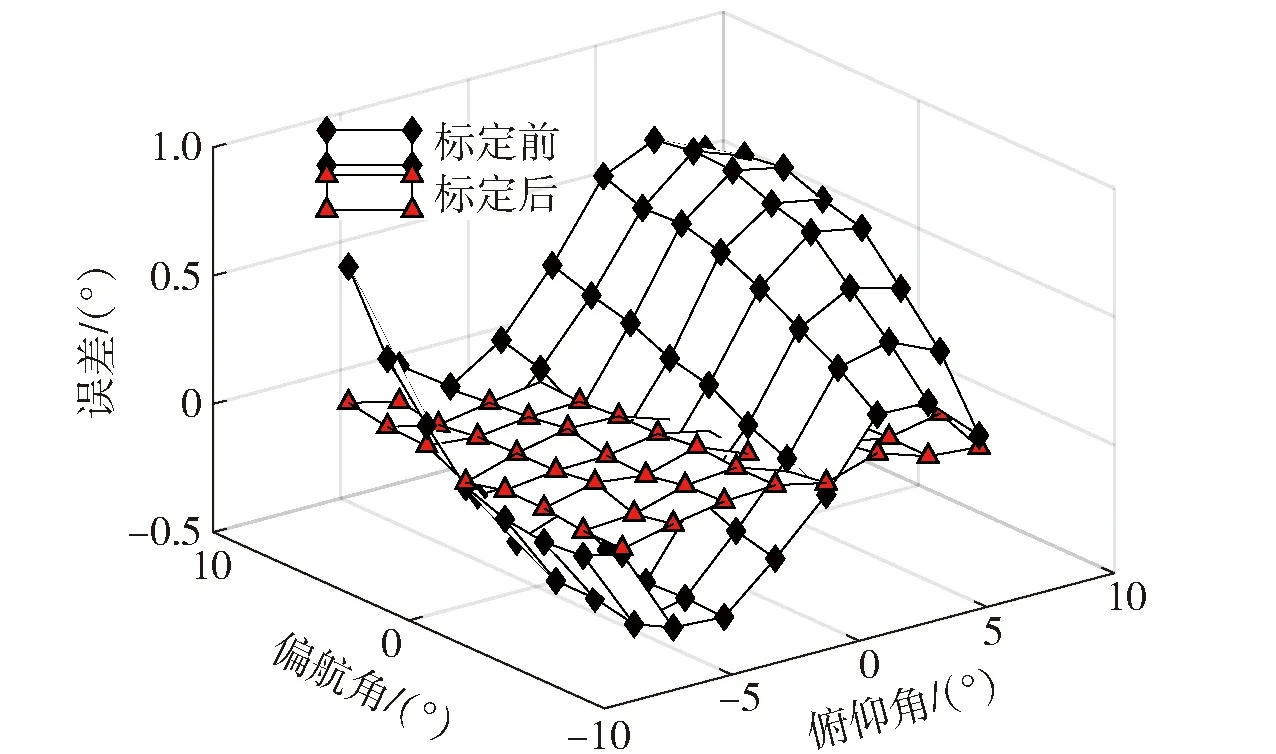
图5 俯仰角误差分布Fig.5 Distribution of pitch angle errors

图6 偏航角误差分布Fig.6 Distribution of yaw angle errors

图7 标定前和标定后俯仰角、偏航角误差统计Fig.7 Statistic values of pitch and yaw angle errors

4 结论

本文首先分析某激光捷联导引头误差来源，结合各项误差特点提出应用分块三次多项式标定其系统误差的方法；其次给出该方法的数学原理；最后设计实验，考虑随机误差的影响，通过实验对所提方法进行验证。该方法与现有方法比，可以避免参数建模的困难，更适应本研究对象测角误差标定；根据所提方法数学原理，采用分块三次插值，可以对误差数据进行更好拟合，提高标定精度；标定过程中与现有方法比，考虑随机误差对标定系统误差的影响，标定结果更可靠。针对上述所提方法，开展标定实验，实验结果证明此方法有效可靠、简单易行、容易推广，对工程实践具有参考应用价值。