基于换乘导向的大型客运枢纽高铁列车接续优化

乔俊 孟学雷 王东先 汤霖

摘 要：针对高速铁路成网条件下的客运枢纽高铁列车接续优化问题，分析了枢纽内的旅客换乘过程，提出了中长途客流的换乘满意度概念;以平均换乘满意度和枢纽车站列车到发均衡性为优化目标，以大站合理发车时间、合理终到时间、车站作业间隔时间、旅客换乘时间、车站到发线能力等为约束条件，建立了基于换乘协同的大型客运枢纽高速列车接续优化模型。设计了改进染色体编码方式和选择策略的遗传算法对算例进行了求解。改进后的遗传算法同基本遗传算法、基本模拟退火算法相比，目标函数中所求的平均换乘满意度分别增加了5.10%、2.93%，枢纽车站列车到发均衡性分别提高了0.27%、2.31%，算例结果验证了改进遗传算法的有效性和稳定性，表明所提方法可以有效地提高大型枢纽高铁列车的接续质量。

关键词：换乘满意度;同站换乘;异站换乘;列车接续;改进遗传算法

中图分类号：TP301.6

文献标志码：A

High-speed train connection optimization for large passenger transport hub based on transfer orientation

QIAO Jun1， MENG Xuelei1*， WANG Dongxian1， TANG Lin2

1.School of Traffic and Transportation， Lanzhou Jiaotong University， Lanzhou Gansu 730070， China;

2.Lanzhou Railway Station， China Railway Lanzhou Bureau Group Company Limited， Lanzhou Gansu 730070， China

Abstract：

In view of the optimization of high-speed train connection in passenger transport hub under the condition of high-speed railway network， the concept of transfer satisfaction of medium and long distance passenger flow was proposed by analyzing the passenger transfer process in hub， and a high-speed train connection optimization model for large passenger transport hub based on transfer orientation was proposed with the average transfer satisfaction and the arrival and departure equilibrium of trains at hub stations as the optimization objective and with the constraint conditions of reasonable originating time of large stations， reasonable terminating time， station operation interval time， passenger transfer time and station arrival and departure line capacity. A genetic algorithm with improved chromosome coding mode and selection strategy was designed to solve the example. Compared with the basic genetic algorithm and the basic simulated annealing algorithm， the improved genetic algorithm increases the average transfer satisfaction in the objective function by 5.10% and 2.93% respectively， and raises the equilibrium of arrival and departure of trains at hub stations by 0.27% and 2.31% respectively. The results of the example verify the effectiveness and stability of the improved genetic algorithm， which indicates that the proposed method can effectively optimize the quality of the high-speed train connection in large passenger transport hub.

Key words：

transfer satisfaction; transfer inside one station; transfer between different stations; train connection; improved genetic algorithm

0 引言

我國高速铁路的快速发展使得高铁客流量和换乘客流量逐年攀升，客流种类和换乘方式也越来越多样化。大型高速铁路客运枢纽作为城市对内对外交通衔接的重要节点，枢纽内的换乘问题受到越来越多的重视。科学地分析枢纽的换乘条件，制定合理的换乘接续方案，优化枢纽内换乘接续列车到发时刻的衔接问题，对于保障客流高效地换乘具有重要意义。

近年来，大型铁路客运枢纽的换乘协同问题受到了不少国内外学者的关注。国外学者多通过调整时刻表的方法研究列车接续优化问题，文献[1]研究了铁路与城市公交间的时刻协同问题，以换乘时间和公交运营成本最小为目标，建立了非线性模型并利用遗传算法求解。文献[2]构建了铁路网络时刻表，以换乘时间最小为目标建立了非线性时刻表优化模型，利用遗传算法求解模型，但模型中没有考虑车站到发线能力约束。文献[3]提出通过调整铁路非周期性时刻表减少乘客换乘时间，以列车运行时间、停站时间等为变量，乘客总的换乘等待时间最小为目标建立了混合整数规划模型，利用改进的启发式算法求解了模型，但只对同站换乘进行了研究。文献[4]研究了城市轨道交通换乘可靠性，通过数学推导分析了发车间隔时间、运行时间对换乘等待时间的影响，但并未建立模型对发车间隔时间和运行时间进行优化。文献[5]研究了铁路周期性时刻表下的旅客换乘问题，以换乘旅客的时间损失最少为目标，建立了周期性时刻表优化模型，并通过启发式算法求解了模型，但模型并未考虑不同方向列车之间的需求换乘客流量。文献[6]研究了以换乘需求为导向的轨道交通换乘优化问题，以乘客换乘等待时间最小为目标，构建了线性和改进的非线性优化模型，并利用粒子群算法求解了改进的非线性模型。

目前国内对铁路客运枢纽旅客换乘和列车接续优化问题的研究相对较少。文献[7]研究了城市轨道交通的换乘，以各条线路首列车的发车时刻为变量，乘客总的换乘等待时间最小为目标，建立了城市軌道交通网列车时刻表优化模型，运用CPLEX工具进行了求解，但并未考虑需求换乘客流量约束以及发车间隔较大线路间的列车接续问题。文献[8]研究了铁路枢纽与城市公交间的接驳问题，以乘客总的换乘时间最小为目标，公交发车间隔、载客量等为约束建立了枢纽换乘时间调度模型。文献[9]分析了铁路枢纽内的同站和异站换乘过程，提出了换乘条件评价指标，但并未利用这些评价指标对枢纽列车接续优化进行深入研究。文献[10]分析了欧洲铁路旅客换乘组织和列车衔接方案，提出我国铁路应当将列车衔接方案与开行方案、运行图的编制过程结合起来，为优化枢纽列车接续问题提供了解决思路。文献[11]以有效换乘客流量最大和换乘无效等待时间最短为目标建立了列车接续优化模型，但模型没有考虑枢纽车站列车的到发均衡性和异站换乘。总的来说，上述文献[1-3，6-8，11]研究目标多为换乘等待时间最小，约束条件[1-3，5，8，11]多为乘客必要换乘时间、列车停站时间、发车间隔时间等，且大多通过调整时刻表[1-3，5，7，11]优化了列车接续问题，这些研究成果为本文提供了重要参考，但研究问题多限于枢纽内单一客运站不同交通方式之间的换乘和轨道交通换乘，异站换乘的研究较少，且算法设计时大多未将车次与到发时刻相结合。鲜有文献在已知开行方案的基础上，通过优化与编排一定周期内换乘枢纽车站的所有列车到发顺序和时间的方法来研究列车接续问题。

针对这些问题，对不同线路及方向的中长途客流在枢纽内的同站、异站换乘优化问题进行研究，以枢纽内需求换乘客流的平均换乘满意度最大化和枢纽车站列车到发均衡性最大化为目标，构建了基于换乘导向的枢纽高铁列车接续优化模型，并设计改进染色体编码方式和选择策略的遗传算法进行求解。

1 问题描述

1.1 同站换乘过程

通常，大型客运枢纽高铁站均设有专门的中转换乘通道，同站换乘旅客可以实现不出站换乘，整个换乘过程为旅客下车步行至接续列车停靠站台候车（或至专用候车室候车）然后检票完成上车。

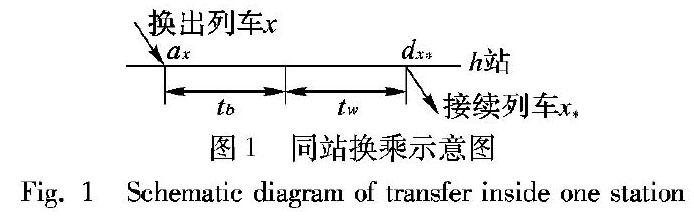
如图1，定义从换出列车x到达车站h时刻ax起至接续列车x从同一车站h出发时刻dx止的时间为同站换乘时间，包括两部分：一是旅客从换出列车下车步行至接续列车停靠站台（或至专用候车室）时止的必要走行时间tb;二是旅客从到达接续列车站台或专用候车室时起至接续列车出发时止的等待时间tw。

tb按照实际查定取值，等待时间tw受两个因素影响，一是接续列车开行频率和开行均衡性，二是换乘衔接方案。理论上来讲，等待时间tw最小值为0，最大值为接续列车的开行间隔时间。

1.2 异站换乘过程

由于枢纽内不同高铁站衔接的干线方向不同，部分起点和终点不在一个方向和线路的中长途旅客为了完成其旅行过程，通常需要在一个换乘枢纽内的不同车站间进行中转，而从一个车站到另一车站，中间需要乘坐城市公共交通。

如图2，定义从换出列车x到达车站h时刻ax起至接续列车x从另一车站h出发时刻dx止的时间为异站换乘时间，包括5个部分：一是旅客从换出列车下车步行至公共交通站台的必要走行时间tb′;二是旅客从到达公共交通站台到等待公共交通上车的公共交通候车时间tw′;三是旅客乘坐城市公共交通从h车站到另一接续车站h的公共交通旅行时间时间t公;四是旅客从另一公共交通站台步行至接续车站检票至候车室的必要走行时间tb″;五是旅客从接续车站候车室时起至完成上车，接续列车出发时止的等待时间tw。

其中tb′、tw′、t公按照不同城市公共交通的异站换乘客流分担率、发车间隔、旅行速度等结合实际查定取值，参考文献[12-15]可知，当枢纽采用以轨道交通为主的集疏运模式时，轨道交通、公交、出租车和社会车辆的换乘客流分担率一般分别为60%、30%、10%;tb″的取值要考虑旅客进站排队检票和安检过程;tw取值原则与同站换乘一致。

2 枢纽内换乘接续优化模型的构建

2.1 模型假设

本文的研究基于以下假设：1）已知研究周期内枢纽各个高铁站的高速列车开行方案，且不存在不停车通过枢纽的高速列车;2）已知研究周期内枢纽不同高速列车之间的需求换乘乘客流量预测值;3）不考虑高速列车运行晚点情况;4）同一线路同一方向、同一线路相反方向间不存在高速列车接续;5）研究周期内的换乘客流在整个旅行过程中只进行一次换乘，且在所研究的枢纽内完成换乘;6）本文只考虑同方向列车的换乘接续情况。

14Jmn（dmnj+2x″h-dmnjxh-2Emndh）2]（4）

其中：x，x′，x″∈Xmnah;x，x′，x″∈Xmndh;Emnah=（T2-T1）/Iahmn，Emnah表示枢纽h站连接的m线路n方向上的列车平均到达间隔时间;Emndh=（T2-T1）/Idhmn，Emndh表示枢纽h站连接的m线路n方向上的列车平均出发间隔时间。

2.4 约束条件

本文主要从高铁站列车合理到发时间、换乘客流量、旅客换乘时间、车站间隔时间等方面对模型进行约束：

1）高速列车合理到发时间约束。

amnixh-Tmnxh≥DmnE（5）

dmnjxh-Tmnxh≤AmnL（6）

T1≤amnixh≤T2（7）

T1≤dmnjxh≤T2（8）

式（5）表示到达枢纽车站的高速列车在其始发站的始发时刻不早于始发车站的最早发车时刻;式（6）表示离开枢纽车站的高速列车到达其终点站的时刻不晚于终到车站的最晚终到时刻;式（7）、（8）表示枢纽车站的列车到发时刻应在研究周期内。

2）换乘客流量约束。

pqxjmnxi≥f（Qpqx*jmnxi，Q）; x≠x*且m≠p（9）

f（μ1， μ2）=1， μ1≥μ2

0，μ1<μ2（10）

表示m线路n方向上第i列到达枢纽且车次为x的列车与p线路q方向上第j列离开枢纽且车次为x*的列车之间的接续关系由两列车之间的换乘客流量决定。

3）换乘时间约束。

Tsmin≤pqx*jmnxi（dpqjx*h-amnixh）≤Tsmax;m≠p，x≠x*（11）

Tdmin≤pqx*jmnxi（dpqjx*h-amnixh*）≤Tdmax;

h≠h*， m≠p， x≠x*（12）

式（11）、（12）表示若列车x与x*构成接续关系，则两列车在枢纽车站的出发和到达时刻差要满足换乘时间约束。

4）通过列车停站时间约束。

thmin≤dpqjxh-amnixh≤thmax; m=p时，q≠n（13）

5）车站间隔时间约束。

amni+1x′h-amnixh≥Iaa（14）

dmnj+1x′*h-dmnjxh≥Idd（15）

dmnjxh-amnixh≥Iad（16）

amnixh-dmnjxh≥Ida（17）

式（14）～（17）表示枢纽车站同方向两列车到发的时间间隔应满足车站的列车到达、出发、到发、发到时间间隔约束。

6）枢纽车站到发线能力约束。

对于任意时刻t，有如下约束：

G（ψv，t）=1， ψv≤t

0，ψv>t; v∈{1，2}（18）

ψ1（dmnjx*h，amnixh，whxx*）=

whxx*（dmnjx*h-Tb），  whxx*=-1

whxx*+1（amnixh-Tap），whxx*=0

whxx*（amnixh-Tap）， whxx*=1（19）

ψ2（dmnjxh，amnixh，whxx）=

whxx（dmnjxh-Tde），  whxx=-1

whxx+1（dmnjxh-Tde），whxx=0

whxx（amnixh-Ta），whxx=1（20）

∑2m=1∑2n=1∑Jmnj=1∑Imni=1[G（ψ1，t）-G（ψ2，t）]≤dfh（21）

式（19）、（20）中引入参数whxx表示列车x或x在枢纽内h站的停站方式，whxx取-1表示始发列车，whxx取0表示通过列车，whxx取1表示终到列车。ψ1（dmnjxh，amnixh，whxx）表示列车开始占用到发线的时间函数，ψ2（dmnjxh，amnixh，whxx）表示列车结束占用到发线的时间函数。

7）区间通过能力约束。

cra+crd≤CrT（22）

3 算法设计及算例分析

3.1 改进遗传算法设计

遗传算法在求解一些复杂的非线性问题时能发挥其全局搜索优势，且在铁路运输组织优化方面取得了广泛应用。由于模型为多目标非线性整数规划模型，为了便于求解，得到研究周期内的枢纽车站所有列车到发时刻，因而将多目标转换成单目标模型求解。由于两个目标函数的量纲和量级不同，首先应统一量纲和量级，使得目标函数规范化，转换后的目标函数如式（23），式中Z2，min、Z2，max表示到发均衡性最小值和最大值，λ为加权系数。

min Z=λ（-Z1）+（1-λ）Z2-Z2，minZ2，max-Z2，min（23）

采用改进染色体编码和选择策略的遗传算法，设计的算法步骤如下：

1）构造基因编码和染色体。

本文关于换乘枢纽车站列车到发时间编排问题的研究对象包括车次、线路、方向、到达（出发）车站、到达（出发）顺序和时间。编码时将车次和车次对应的到达（出发）时刻构成一个元组，作为本文遗传算法的基因，并采用两段式染色体編码方式，以换乘枢纽内存在两个高铁站，枢纽连接两条线路，且两车站之间存在联络线为例，构造如图3所示的染色体编码结构：第一部分表示枢纽内两个车站的各个线路各个方向的列车依次到达（出发）时刻编排，依次为h站1线路1方向到达、h站1线路1方向出发、h站1线路2方向到达（出发）、h站2线路1方向到达（出发）、h站2线路2方向到达（出发）以及h站各个线路和方向的列车到发时间编排;第二部分表示不同车站不同线路和方向的列车依次到达和出发时刻之间的断点位置。

2）初始种群的生成。

由于研究周期[T1，T2]内每个个体染色体基因中的实数编码、整数编码分别表示到达（离开）枢纽车站的列车车次和对应列车在枢纽车站的到达（出发）时刻，首先随机生成一个枢纽车站所有线路和方向不重复的到达（出发）车次序列，其次生成该车次序列对应的列车到达（出发）时刻，由于列车到达（出发）时刻是按照时间序排列的，因此每个个体的染色体基因段中的列车到达（出发）时刻应该是Xmnah（Xmndh）这些车次的到达（出发）时刻的升序排列。因此可以按照以下方法得到两个断点之间列车出发时刻升序排列的染色体片段：

①在[T1，T2]内生成一个随机数t1，作为dmn1xh;

②在[t1，T2]内生成一个随机数t2，作为dmn2x′h;

③依此类推，在[tj-1，T2]内随机生成tj作为h站发往m线路n方向第j列车的出发时刻。

同理可以生成染色体中任意两个断点之间的列车到达时刻升序排列片段，并将这些片段组成完整的染色体个体。

3）适应度函数。

设K为种群规模，Zk是当前种群中的第k个染色体的目标函数值，Zmax和Zmin分别为当前种群的最大、最小目标函数值，gk为适应度函数。

gk=Zmax-Zk+γZmax-Zmin+γ; k∈{1，2，…，K}（24）

其中：γ是（0，1）内的随机数，引入γ使得当染色体间的适应值差距较大时，采用适应值比例选择，当染色体间的适应值差距较小时，则在相互竞争的染色体中进行纯随机的选择。这样使表现较优的个体适应度更大，进入下一代的几率也更大。

4）改进选择算子。

文中应用如下混合改进了的选择方案，将选择操作分为以下3个步骤：

①将计算得到的个体适应度按照从大到小进行排序，保留父代种群中的前1/4个体[16];

②随机在父代种群中选取1/2K个个体，K为种群规模（排除①中选中的个体）按照下文的5）交叉算子和6）变异算子生成新子代[16];

③将①中选择出的个体与②中生成的新子代进行模拟退火选择，其次将模拟退火选择之后得到的个体与原父代种群合并组成临时种群，设临时种群规模为K′，临时种群中每个个体为k′，则保证了随着算法迭代次数的下降，改进算法的临时种群规模K′始终大于种群规模K。依据改进方法，借鉴模拟退火算法，将各个染色体的适应度函数值进行拉伸[17]，运用式（25）计算临时种群中每个个体k′被选择的概率，从临时种群中选出K个个体组成新的一代进行下一轮遗传算法操作：

P（k′）=eg（k′）/Tv′/∑K′k′=0eg（k′）/Tv′; k′∈{1，2，…，K′}（25）

Tv′=1ln（v′/T0+1）（26）

其中：Tv′为渐趋于0的退火温度（v′=1，2，…），T0为初始温度。改进的选择算子借鉴了模拟退火算法中的拉伸方法，可以改善基本遗传算法的早熟问题，同时使得在遗传算法后期过程中，当个体染色体适应度趋于一致时，改进的算法具有更好的选择效果，同时这一选择算子不仅包含了父代种群中的最佳个体，保证了算法的收敛性，又保留了最优个体以外的优秀个体，增加了种群的多样性，避免算法陷入局部最优解。

5）交叉算子。

文中的染色体是由不同片段的车次实数编码和列车有序到（发）时刻整数编码元组构成，采用传统的交叉方法不能得到理想的结果，因此本文采用区域交叉，将交叉区域限定在两个相邻的断点之间，并将交叉区域的到（发）时刻值与另一个群体基因位的时刻值进行比较，交叉时车次不随时刻交叉，具体操作步骤如下：

①在父代种群中，随机选择两个个体作为父代1和父代2，并随机选取两个相邻断点之间的两个交叉点，规定父代1和父代2的两个相邻断点的选择相同。将这两个交叉点之间的所有时刻基因值作为交叉对象进行交叉操作。

②将父代2交叉区域内的时刻基因值分别与父代1中所有的时刻基因值之差的绝对值进行比较。若差值为0，则父代1中的基因值不变;若差值不为0，则将交叉区域内的时刻基因值与父代1中绝对值最小的基因位上的时刻值进行替换，若存在两个基因时刻值的绝对值相等，则将父代1中对应的时刻基因值较大的时刻值替换，从而得到交叉后的子代1，同理可以得到交叉后的子代2。例如某两个相邻断点之间的交叉操作如图4和图5。

6）变异算子。

在染色体个体变异之前，为了避免算法陷入局部最优，同时得到研究周期内枢纽车站最优的列车到发顺序，应随机生成K个不同的枢纽车站所有线路方向不重复的到发车次序列替换上述交叉后的子代染色体基因中的车次序列。

采用均勻变异，将每条染色体上的一个或多个基因点设置为变异点，以一定的变异概率Pm确定一个随机数，并确定变异点的取值范围，以变异后的值取代变异点先前的取值，变异时基因元组中的车次不变。例如，随机选中的一个个体k，个体k中的amnixh为变异点，amnixh的取值范围为[amnixh-σ，amnixh+σ]。变异点的新基因值为：

a′mnixh=amnixh-σ+β[（amnixh+σ）-（amnixh-σ）]（27）

其中β∈（0，1），是一个随机数。

7）终止条件。

设定改进的遗传算法最大进化代数，当遗传算法运行到最大进化代数之后，停止运行，输出结果;否则转步骤3）。

3.2 算例分析

选择高速铁路网中某一大型枢纽，枢纽衔接两条高速铁路线路，存在两个高铁站且两车站之间存在联络线，该枢纽采用以轨道交通为主的客流集疏运模式，图6是研究客运枢纽的换乘接续示意图。

该枢纽详细概况如下：dfh1、dfh2为14条、13条;thmin、thmax分别为3min、20min;Iaa、Idd、Ida、Iad分别为2min、2min、3min、3min;tap、tde、tb、ta分别为5min、2min、23min、20min;D11E、D12E、D21E、D22E分别为360、390、330、420;A11L、A12L、A21L、A22L分别为1380、1380、1440、1380;C1T、C2T、C3T、C4T分别为16、7、12、10。选

取该枢纽的中长途旅客换乘时段13：00—14：00作为研究周期，枢纽内两个高铁站的列车开行方案如表1所示。由于文献[11-12，18]研究枢纽与文中所研究枢纽概况、换乘客流量相当，因而推算得出研究周期内不同列车间的换乘客流量预测值，如表2所示。

根据文献[11，18]，结合所研究枢纽的概况、换乘客流量、铁路部门的成本和收益等因素综合确定换乘接续列车判定接续旅客人数Q为50人。同时为了保证旅客能够在一定时间内顺利完成换乘，Tsmin、Tsmax按照枢纽内客流高峰时段的乘客必要走行时间、检票时间以及接续列车开行间隔时间来取值，分别取15min、45min;Tdmin、Tdmax结合枢纽内客流高峰时段的乘客必要走行时间、检票时间、接续列车开行间隔时间、城市公共交通的运行时间和换乘客流的分担率取值，分别取40min、70min。

遗传算法的参数设置为：种群规模K取300，交叉概率pc取0.75，变异概率pm取0.06，最大迭代次数1000，T0初始温度取为100，λ取0.6。依据上述模型和算法，利用Matlab R2014a软件工具编程求解算例，分别运用基本遗传算法和改进的遗传算法对算例求解，得到改进后遗传算法的优化结果如表3和表4，目标函数为-0.1257，其中目标值Z1满意度为0.6367，目标值Z2列车到发均衡性值为640.5826，以及目标函数随迭代次数变化示意图8。

鉴于本文设计改进的遗传算法结合了模拟退火算法的思想，因此，本文又以基本模拟退火算法作为对比算法，在同一台计算机上利用Matlab编程实现基本模拟退火算法求解模型，通过进行多次实验，得到基本模拟退火算法计算的结果为：算法迭代了696次之后，目标函数值趋于稳定且到达最小，此时求得的目标函数值为-0.1088，其中目标值Z1满意度为0.6186，目标值Z2列车到发均衡性值为655.7341，进一步将基本模拟退火算法、基本遗传算法以及本文改进的遗传算法进行比较，如表5所示。

在枢纽客流换乘满意度方面，分析表3和表4可以看出，12对列车实现了有效接续，其中7对列车的接续时间使得换乘客流满意度达到60%以上，1对列车的接续时间使得换乘客流满意度最低。同时由表4求得该枢纽换乘客流的平均同站换乘时间为27min，平均异站换乘时间为49.83min。

在枢纽列车到发均衡性方面，h2站连接的2线路2方向列车到达和2线路1方向列车出发、h1站连接的1线路2方向列车出发和2线路1方向列车到达，这几个方向的列车到发均

衡性较优，而h1站连接的1线路列车到发均衡性较差。总的来说，h2站的列车到发均衡性较h1站更优。

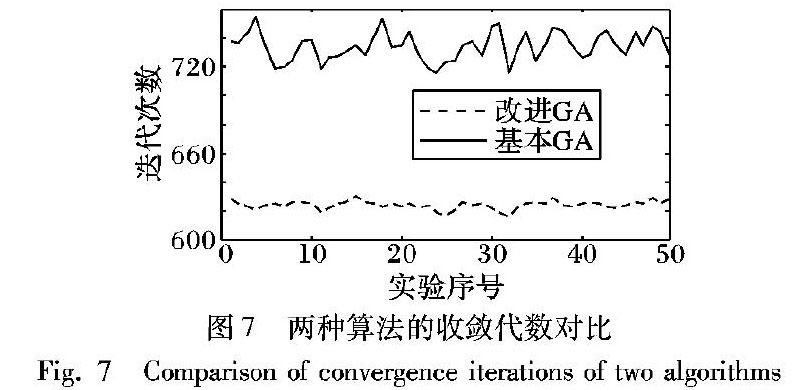
为了进一步验证改进后遗传算法的稳定性，分别运用基本遗传算法和改进遗传算法对算例求解，图7是随机抽取的50次实验结果的收敛代数情况。可以看出，在种群规模和迭代次数相同的情况下，改进后的遗传算法稳定性更好。

利用本文模型和改进的遗传算法对高速铁路网中某一大型客运枢纽高速列车接续问题进行优化，得到目标函数值随迭代次数变化情况，如图8所示。

由于本文设计的遗传算法结合所研究问题设计了两段式染色体编码方式，将车次和车次对应的到达（出发）时刻构成一个元组即设计的算法基因，并在选择算子中融入了模拟退火算法的拉伸方法和退火选择，将遗传算法全局寻优能力强的特点和模拟退火算法局部寻优能力强的特点相结合，使得改进的遗传算法具有更好的选择效果，有效地提高了本文设计算法的解的质量。由表5可知，对比基本模拟退火算法，本文改进的遗传算法，目标函数值更优，其中旅客平均换乘满意度增加约2.93%，到发均衡性增加约2.31%，旅客无效等待时间更少，h1站和h2站两个车站的列车到发均衡性指标值的差异更小;对比基本遗传算法，本文改进的遗传算法使得旅客平均换乘满意度增加约5.10%，到发均衡性增加约0.27%，且求得的目标函数值、平均无效等待时间、h1站和h2站兩个车站的列车到发均衡性指标差异均比基本遗传算法求得的解更优。

由以上分析结果可知，本文设计改进的遗传算法更加适合所研究问题的模型特征，具有更快的收敛速度和更优的求解性能，因此，文中基于换乘的高速铁路枢纽列车接续优化模型和改进的遗传算法能够对换乘枢纽的列车接续优化问题进行有效求解。

利用本文的模型和改进遗传算法对算例中的大型客运枢纽高铁列车接续进行优化，算法迭代了623次之后，目标函数值趋于稳定且达到最小，得到目标函数值随迭代次数变化情况如图8所示。

4 结语

1） 通过优化与编排周期内换乘枢纽车站的所有列车到发顺序的方法来研究换乘枢纽列车接续问题。建立基于换乘导向的大型高速铁路枢纽列车接续优化模型，以换乘客流的平均换乘满意度和枢纽车站列车到发均衡性为目标，考虑大站合理发车时间、换乘时间、车站间隔时间等约束，为解决换乘枢纽列车接续问题提供了理论基础和方法借鉴。

2） 定义了换乘满意度函数，在求解模型时将多目标问题转化成单目标问题，借助于改进染色体编码方式和选择策略的遗传算法，有效地求解了模型。研究结果优化了换乘枢纽车站的列车接续问题，验证了模型和算法的有效性。

3） 通过对改进的遗传算法与基本遗传算法、基本模拟退火算法进行比较，可以看出本文设计的改进遗传算法不仅稳定性和求解效率更高，且求得的解的质量更优，对文中问题求解具有较好的适应性。

4） 模型未考虑换出列车或接续列车发生晚点时的列车接续问题，对于这一问题的研究将是后续工作的重点。

参考文献

[1]SHRIVASTAVA P， DHINGRA S L. Development of coordinated schedules using genetic algorithms [J]. Journal of Transportation Engineering， 2002， 128（1）： 89-96.

[2]YANG Z， KOSEKI T， SONE S. Railway network timetabling for reducing transfer time using genetic algorithm [J]. IEEJ Transactions on Sensors and Micromachines， 2008， 120（6）： 802-809.

[3]WONG R C W， YUEN T W Y， FUNG K W， et al. Optimizing timetable synchronization for rail mass transit [J]. Transportation Science， 2008， 42（1）： 57-69.

[4]MULLER T H J， FURTH P G. Transfer scheduling and control to reduce passenger waiting time [J]. Transportation Research Record： Journal of the Transportation Research Board， 2009， 3（2112）： 111-118.

[5]MESA J A， ORTEGA F A， POZO M A， et al. Rescheduling railway timetables in presence of passenger transfers between lines within a transportation network [M]// de SOUSA J F， ROSSI R. Computer-based Modelling and Optimization in Transportation， AISC 262. Berlin： Springer， 2014： 347-360.

[6]HASSANNAYEBI E， ZEGORDI S H， YAGHINI M， et al. Timetable optimization models and methods for minimizing passenger waiting time at public transit terminals [J]. Transportation Planning and Technology， 2017， 40（3）： 278-304.

[7]禹丹丹，韩宝明，董宝田，等.基于换乘协同的轨道交通网列车时刻表优化模型[J]. 中国铁道科学，2015，36（4）：129-135.（YU D D， HAN B M， DONG B T， et al. Optimization model of train timetable for rail transit network based on transfer synchronization [J]. China Railway Science， 2015， 36（4）： 129-135.）

[8]姚凤金，杨浩.旅客枢纽换乘时间调度研究[J].交通运输系统工程与信息，2008，8（1）：133-137.（YAO F J， YANG H. On transferring time scheduling of passenger hubs [J]. Journal of Transportation Systems Engineering and Information Technology， 2008， 8（1）： 133-137.）

[9]郭瑾.高速铁路综合枢纽换乘条件评价及应用研究[D].北京：北京交通大学，2011：33-59.（GUO J. Research on evaluation and application of transfer condition for integrated hub of high-speed railway [D]. Beijing： Beijing Jiaotong University， 2011： 33-59.）

[10]郭根材，聶磊，贺振欢，等.基于欧洲列车时刻表的高速列车衔接方案探讨[J]. 北京交通大学学报，2012，36（6）： 21-26. （GUO G C， NIE L， HE Z H， et al. Train connection plan for high-speed railway based on European rail timetable [J]. Journal of Beijing Jiaotong University， 2012， 36（6）： 21-26.）

[11]黄曲.大型换乘站旅客列车接续方案优化研究[D].成都：西南交通大学，2018：38-39.（HUANG Q. Research on optimization of passenger train connection scheme in large transfer station [D]. Chengdu： Southwest Jiaotong University， 2018： 38-39.）

[12]王建聪.城市客运枢纽换乘组织关键问题研究[D].北京：北京交通大学，2006： 30-31.（WANG J C. Key issues on transfer organization of city passenger traffic hubs [D]. Beijing： Beijing Jiaotong University， 2006： 30-31.）

[13]谢仲磊.高铁枢纽与城市路网的衔接分析[J]. 交通与运输，2018，34（4）：12-14.（XIE Z L. Analysis of connection between high-speed railway hub and urban road network [J]. Traffic and Transportation， 2018， 34（4）： 12-14.）

[14]张发才.铁路客运与城市交通运营组织衔接研究[D].南京：东南大学，2006：24-28. （ZHANG F C. Study on passenger transfer of operation between railway station and urban traffic [D]. Nanjing： Southeast University， 2006： 24-28.）

[15]周军.高铁客运枢纽与城市交通衔接方式优化研究[D].武汉：武汉理工大学，2013： 44-46.（ZHOU J. Study on the optimization of high-speed passenger transport hubs urban transportation mode [D]. Wuhan： Wuhan University of Technology， 2013： 44-46.）

[16]李政伟，谭国俊.改进的退火遗传优化策略应用研究[J].计算机工程与应用，2010，46（4）：245-248. （LI Z W， TAN G J. Research and application of improved simulated annealing genetic strategy [J]. Computer Engineering and Applications， 2010， 46（4）： 245-248.）

[17]刘月娥，何东健，李峥嵘.一种用于BP网络优化的并行模拟退火遗传算法[J].计算机应用，2006，26（1）：204-206.（LIU Y E， HE D J， LI Z R. Parallel simulated anneling genetic algorithm for optimizing BP neural network [J]. Journal of Computer Applications， 2006， 26（1）： 204-206.）

[18]王瑩.面向超长距离客流的高速铁路网络化列车开行方案研究[D].北京：北京交通大学，2018：138-140.（WANG Y. Study on high-speed railway network line planning for extra-long distance passenger flow [D]. Beijing： Beijing Jiaotong University， 2018： 138-140.）

This work is partially supported by the National Natural Science Foundation of China （71861022， 61563028）.

QIAO Jun， born in 1993， M. S. candidate. Her research interests include operation management and decision optimization of rail transit.

MENG Xuelei， born in 1979， Ph. D.， professor. His research interests include operation management and decision optimization of rail transit.

WANG Dongxian， born in 1992， M. S. candidate. His research interests include operation management and decision optimization of rail transit.

TANG Lin， born in 1989， M. S. His research interests include operation management and decision optimization of rail transit.