无能级稳定判据的多尺度量子谐振子算法
王德志 王鹏


摘 要:多尺度量子谐振子算法是一种基于量子理论构建的智能优化算法。能级稳定过程是该算法的核心迭代过程之一,能级稳定判据是判断算法是否达到暂稳态的条件。通过对算法物理模型的分析,可知算法在初始采样阶段每一次迭代操作都是能级下降的过程,所以取消能级稳定判据,也可实现算法从高能态过渡到暂稳态直至基态的进化过程。无能级稳定判据的算法在6个标准测试函数上的结果显示其在求解精度、成功率、迭代次数上均表现出了优异的性能,算法的波函数显示无能级稳定判据的算法仍然可以完成从高能态到基态的收敛,且无能级稳定判据的算法在结构上更加简洁,易用性更高,实现难度更低。无能级稳定判据的多尺度量子谐振子算法能够以更加简洁且有效的方式进行应用。
关键词:多尺度量子谐振子算法;优化算法;能级稳定;量子模型;成功率;波函数
中图分类号:TP301.6
文献标志码:A
Multi-scale quantum harmonic oscillator algorithm without energy level stability criterion
WANG Dezhi, WANG Peng*
School of Computer Science and Technology, Southwest Minzu University, Chengdu Sichuan 610041, China
Abstract:
Multi-scale quantum harmonic oscillator algorithm is an intelligent optimization algorithm based on quantum theory. The energy level stabilization process is one of the core iterative processes of the algorithm, and the energy level stability criterion is the condition for judging whether the algorithm reaches metastable state. Through the analysis of the physical model of the algorithm, it was considered that each iteration of the algorithm in the initial sampling stage is a process of energy level descent, so that the algorithm without energy level stability criterion was also able to realize the evolution from high energy state to metastable state until ground state. The results of the algorithm without energy level stability criterion on six standard test functions show the excellent performance of the algorithm in terms of solution accuracy, success rate and number of iterations. The wave function of the algorithm shows that the algorithm without energy level stability criterion can still converge from the high-energy state to the ground state, and is simpler in structure, easier to use and less difficult to implement. Multi-scale quantum oscillator algorithm without energy level stability criterion can be applied in a more concise and efficient way.
Key words:
multi-scale quantum harmonic oscillator algorithm; optimization algorithm; energy level stability; quantum model; success rate; wave function
0 引言
利用物理模型構建智能优化算法是一种非常有效的方法,例如模拟退火算法(Simulated Annealing Algorithm, SAA)是基于1953年提出的Metropolis选择准则构造的[1],核心思想是当算法陷入局部最优时,接受一个比当前解更差的解,以此跳出局部最优。量子粒子群优化(Quantum-behaved Particle Swarm Optimization, QPSO)算法利用δ势阱下的量子波函数构造粒子进化公式,通过不断减小特征长度逐步实现局域化的新解采样,从而达到算法收敛的目的[2]。多尺度量子谐振子算法(Multi-Scale Quantum Harmonic Oscillator Algorithm, MQHOA)也是一种利用物理模型构建的智能优化算法,MQHOA利用量子波函数的概率解释来模拟算法的采样过程,从而完成算法的求解。文献[3]给出了MQHOA的完整实现方法,并对算法进行了详细的介绍。另外MQHOA在多峰优化问题上也表现出了较好的性能,并提出了一种用于多模优化的MQHOA的变种[4]。文献[5]详细阐述了MQHOA的物理模型和数学分析,通过与遗传算法、模拟退火算法、粒子群算法和量子粒子群算法进行对比,结果表明,MQHOA在收敛速度和最优解精度方面具有竞争优势和优越性。2016年,研究团队提出了具有能级稳定过程的多尺度量子谐振子算法,算法的基本框架包括能级稳定过程、能级降低过程和尺度降低过程[6]。MQHOA的特别之处在于采样的方式是利用高斯分布的中心位置进行采样,这种采样方式是非均匀采样中的重要采样方法,可以使重要区域的采样密度相对较高,靠近最优解的采样密度相对较高,从而提高采样效率、减少采样次数。同时,MQHOA在实际工程领域也得到了应用,在云计算任务调度[7]、相空间聚类[8]中都取得了
較好的效果。近期,算法又得到了进一步的改进,文献[9]提出了一种具有严格亚稳态约束MQHOA并在多模态优化中得到应用,MQHOA利用群统计策略来评估群体的状态并忽略个体状态,引入了严格的亚稳态约束策略。增强了在局部区域找到更好质量解决方案的能力。文献[10]提出了一种具有截断平均稳定策略的MQHOA,并用于求解全局数值优化问题。理论和实验分析表明,三重均值稳定策略能在一定程度上提高收敛效率。
从构建算法的物理模型来分析[11],能级稳定判据并不是算法整体框架内的必须条件。能级稳定判据的存在并没有对应的物理意义可以解释,反而增加了算法采样过程中不必要的动作。本文尝试将MQHOA中的能级稳定判据去除,进一步简化MQHOA的基本框架,提出了一种无能级稳定判据的MQHOA,文中将有能级稳定判据的算法成为多尺度量子谐振子算法A版本(Multi-scale Quantum Harmonic Oscillator Algorithm A, MQHOA-A),无能级稳定判据的算法成为多尺度量子谐振子算法B版本(Multi-scale Quantum Harmonic Oscillator Algorithm B, MQHOA-B)。
1 MQHOA物理模型
多尺度量子谐振子算法以量子理论中波函数的物理意义为基础,模拟谐振子的运动过程,建立了算法的基本思想。在量子力学中粒子出现的机率可以用波函数(wave function)进行描述,但波函数既不能描述粒子的轨迹也不能描述粒子的形状,对于任意粒子只能依据波函数给出其位置分布的概率。描述量子系统的方程称为薛定谔方程,它可以写成如下的形式:
-h2m2x2+V(x) ψ(x)=Eψ(x)(1)
MQHOA算法将优化问题中的目标函数f(x)看作薛定谔方程中的势阱V(x),复杂目标函数f(x)在全局最小值位置x0附近可以采用泰勒序列进行展开:
V(x)=f(x)=f(x0)+f′(x0)(x-x0)+12f″(x0)(x-x0)2+…(2)
在f(x)的泰勒展开中f(x0)为常数,在最小值位置x0处目标函数f′(x0)=0,去除高次项,可以得到:
V(x)=f(x)f(x0)+(1/2) f″(x0)(x-x0)2(3)
函数优化问题在这一对应条件下就转变为求粒子在势阱约束条件下的基态波函数问题。基态波函数代表了量子系统中粒子在能量的基态时的概率分布,而在函数优化中,采样种群在目标函数可行解空间内不断向最优解的方向收敛的过程可以看作是能量不断向基态迁移的过程,因此,基态波函数的概率分布可以看作是目标函数最优解的概率分布。定义算法当前波函数ψ(x)2为k个正态概率分布N(xi,σ2s)的叠加。
ψ(x)2=∑ki=1N(xi,σ2s)=∑ki=112πσs e-(x-xi)22σ2s(4)
从概率上理解波函数ψ(x)2就是当前迭代过程中全局最优解的概率分布,MQHOA算法的全部迭代过程都是为了使波函数的概率分布向最优解的位置集中。能级稳定过程的基本操作是k个正态分布产生的新解不断替换差解的过程。当算法在迭代过程中满足一定约束条件时即认为算法在当前能级下进入暂稳态,这一约束条件就是能级稳定判据。
从物理模型来看,算法在向最优解收敛的过程本身就是能级不断下降的过程。MQHOA中的能级稳定过程在算法的整体框架下显得冗余。能级稳定的判据是人为设定的,在一定程度上与物理模型的实际过程不相符,算法在高能级时的稳定状态对应于物理中的亚稳态,此时采样位置的概率分布一般是位于目标函数的局部最优位置附近,只有算法处于能量较低的基态时,算法才能在当前尺度稳定。本文提出的MQHOA-B算法,在新的框架下,算法更为简洁且更符合量子物理中能级变化的规律。无能级稳定过程及其判据也能实现算法从高能态到基态的收敛。
2 MQHOA基本流程
2.1 MQHOA-A算法流程
MQHOA-A为有能级稳定判据的版本。算法包括能级稳定过程、能级降低过程和尺度降低过程,分别对应于伪代码中的三个while循环。算法迭代的基本操作包括高斯采样和3个收敛判据,需要主观设定的参数只有采样种群个数k,避免了多个控制参数造成的参数设定的困难。能级稳定过程的引入,使MQHOA能在高能级的亚稳态能进行充分的搜索,保证了解的多样性。虽然能级稳定判据的存在,可以增强粒子在寻优过程中搜索能力,但是能级稳定判据是人为设定的,在一定程度上使算法在搜索过程中具有主观性,并对寻优结果有一定的影响。MQHOA-A的伪代码如下所示。
有序号的程序——————————Shift+Alt+Y
程序前
1)
initialize k, σmin, MAX, MIN, σs=MAX-MIN
2)
randomly generate xi (i=1,2,…,k) in [MIN,MAX]
3)
calculate fi=f(xi), fbest=fmin(xi), xbest=xi
4)
calculate the standard deviation σk for all xi
5)
while (σs>σmin) do
6)
while (σk>σs) do
7)
while (Δσk>σs) do
8)
xi, generate xi′~N(xi,σs2)
9)
xi and xi′, if f(xi′)
10)
calculate the standard deviation σk for all xi′
11)
Δσk=|σk-σk′|
12)
end
13)
update the worst solution: xworst=xmean
14)
end
15)
σs=σs/2
16)
end
17)
output xbest, f(xbest)
程序后
2.2 MQHOA-B算法流程
MQHOA-B为无能级稳定判据的版本。算法无需能级稳定判据即可实现第一阶段的采样过程,从代码上看,直接带来的改变就是减少一层循环。算法从三层循环变成两层循环,新版本的算法在一个更加简洁的框架下同样能完成算法的基本搜索过程。算法在无能级稳定过程判据的情况下仍然实现了算法初始阶段的采样过程。无能级稳定判据的算法的整体流程更加符合量子体系中能量变化的特点,更加地贴合物理模型。去掉能级稳定判据,使算法在采样过程中避免了主观的人为干预,算法的求解过程更加客观,提高了结果的可靠性。MQHOA-B的伪代码如下所示。
有序号的程序——————————Shift+Alt+Y
程序前
1)
initialize k,σmin,MIN,MAX,σs=MAX-MIN
2)
randomly generate xi (i=1,2,…,k) in [MIN,MAX]
3)
calculate fi=f(xi), fbest=fmin(xi),xbest=xi
4)
while (σs>σmin) do
5)
while (σk>σs) do
6)
xi,generate x′i~N(xi,σ2s)
7)
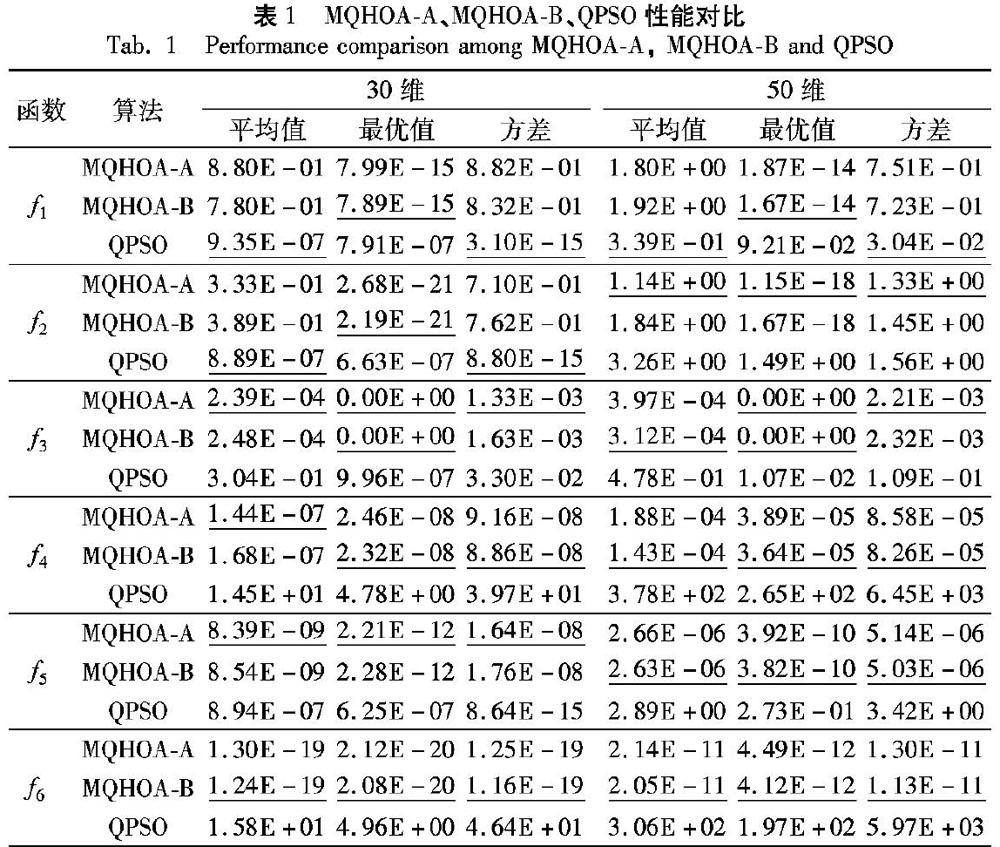
xi and x′i, if f(x′i) 8) calculate the standard deviation σk for all x′i 9) update the worst solution: xworst=xmean 10) end 11) σs=σs/2 12) end 13) output xbest, f(xbest) 程序后 无能级稳定判据的算法具体迭代过程如下: 其中:k是可以人为设置的采样种群个数,σmin表示每个维度上的收敛精度,目标函数的定义域为[MIN,MAX],初始尺度σs=MAX-MIN,算法的结束条件为σs≤σmin。 步骤1 对于每个xi各自按正态分布N(xi,σ2s)生成k个采样位置x′i。 步骤2 计算新位置的函数值,若f(x′i) 变化的绝对值,Δσk=σk-σ′k。对方差进行更新σ′k: σ′k ← σk。 步骤3 用k个当前最优采样位置的均值替换最差解的位置:xworst=xmean。 步骤4 计算当前最优解位置方差σk,如果(σk<σs), 能级降低过程结束,否则转到步骤1。 步骤5 尺度下降过程,尺度减半σs=σs/2,使算法在更小尺度下重复能级的不断从高到低的过程,直至满足收敛条件。 3 实验分析 3.1 实验说明 选择了6个常用的标准测试函数来检测新框架下算法的性能,测试了所有函数在100维以内的情况,对于Griewank函数的测试达到了500维,函数的定义域取值均为[-10,10]。算法的初始采样个数为k=30,算法的收敛精度均为σmin=1×10-6,当求解的目标函数最优值与理论最优值的差的绝对值小于等于1×10-6则认为在这一次的求解成功,成功次数所占51次的比例即为成功率,用GDpercent表示。优化目标函数的维度用DIM表示,在一个维度为d的空间内的粒子xi(i=1~k)可以写为Xi=[xi1,xi2,…,xid],表示该粒子在d个方向上都是有信息分量的。优化目标均是寻找目标函数的全局最小值,本文所选的测试函数理论最优值均为0。实验主要关注算法的成功率、收敛情况以及波函数。所有仿真实验均在Intel Xeon CPU E5-1630 v3 @3.7GHz,16GB内存的计算机上进行,程序采用Matlab 2016a实现。实验选用了6个标准测试函数: f1(Ackley)、 f2(Levy)、 f3(Griewank)、 f4(Quadric)、 f5(Sum Square)、 f6(Zakharov)。 3.2 实验结果与分析 3.2.1 实验结果 在实验的初始阶段,对比了MQHOA-A和MQHOA-B的性能,并引入了QPSO算法作为参照。实验设置了相同的迭代次数,三种算法均设置最大迭代次数为10000×DIM。QPSO的种群规模为30,收缩扩张系数α=1~0.5。主要关注三种算法求解的平均值、最优值和方差,且每种算法得到的结果均是通过重复51次实验得到的统计结果。如表1所示,其中下划线数字为相对较优的结果。实验发現MQHOA-B算法的基本测试结果与MQHOA-A的测试结果相比均表现出良好的性能。两个版本算法的结果在平均值、最优值和方差上无明显差别。QPSO算法在函数f1的优化中表现出较好的收敛性,但是在其他函数的收敛精度表现较差,总体的收敛能力不如MQHOA-A和MQHOA-B。由于QPSO采用的是δ势阱模型,QPSO的优势在于收敛速度快,但是带来的问题是容易导致算法早熟和停滞,特别是在高维函数优化中比较明显。MQHOA-B在6个测试函数的30维和50维上的表现均与MQHOA-A保持在同一水平。两个版本的算法均能以相对较高的精度找到函数的最优解。MQHOA-B在一个更加简洁的框架下运行,依旧能保证较高的求解精度和具有竞争性的收敛能力。从实验结果来看,能级稳定判据并不是MQHOA的必要条件,去掉能级稳定判据,对算法的基本性能并没有大幅度的影响,但是无能级稳定判据的算法(MQHOA-B)在结构上更加清晰,更加符合物理模型,减少了人为干预带来的不客观因素。 3.2.2 成功率分析 如图1(a)、图1(b)、图1(c)、图1(d)、图1(e)、图1(f)所示,分别是MQHOA-A和MQHOA-B在函数f1、 f2、 f3、 f4、 f5、 f6上的成功率情况。从6个标准测试函数的结果来看,10维是一个临界点,其中f1、 f2、 f3在10维以后成功率呈现下降趋势。而在其他函数的优化过程中并没有出现明显的变化,均能以100%的成功率找到最优解。随着函数维度的升高,两个版本的算法的成功率逐渐下降,最后趋于零,总体趋势基本一致。图1(c)为算法在函数f3高维情况下的成功率变化情况,MQHOA-A与MQHOA-B在高维情况下均出现了较大的波动,但是MQHOA-B要相对稳定,总体的波动较小。图1(d)、图1(e)、图1(f)则分别反映了函数f4、 f5、 f6成功率情况,成功率均为100%。从图1中可以看出,MQHOA-B和MQHOA-A的成功率变化基本呈现相同的趋势,但是在高维情况下,MQHOA-B的成功率较为稳定,波动较小。 3.2.3 收敛性分析 收敛性是评价算法的重要指标,本节对比了MQHOA-A和MQHOA-B在6个基本测试函数上的收敛情况。如图2(a)和图2(b)所示,分别是函数f1和f2在10维的时候收敛曲線,MQHOA-B算法均比MQHOA-A收敛得更快,且收敛精度均可达到1×10-5和1×10-10以上。 如图3(a)和图3(b)所示,分别是函数f5和f6在50维的时候的收敛曲线。MQHOA-B同样能以较快的速度收敛,尤其在函数f5上,在迭代次数上比MQHOA-A大概少20万次便收敛到最优解的位置。在函数f6上MQHOA-B与MQHOA-A基本保持在相同的收敛速度,但是在总的迭代次数依旧较少。 如图4(a)和图4(b)所示,分别是函数f3和f4在100维时的收敛曲线。MQHOA-B与MQHOA-A的收敛速度基本一致,但是总的收敛次数仍然较少。 综上,MQHOA-B在收敛速度上基本与MQHOA-A持平,但是总的迭代次数较少。说明MQHOA-B能够以较少的迭代次数收敛到最优解位置,尤其是在高维函数上,体现了MQHOA-B在高维函数优化上的竞争力。 3.2.4 波函数分析 MQHOA的波函数代表了算法在寻优过程中解的概率分布,反映了算法的能级变化过程。在采样的初始阶段,算法处于高能级状态,随着迭代的进行,算法逐渐向最优解的方向移动,能级逐渐下降,当算法到达最优解的位置时,能级处于基态。如图5(a)、图5(b)、图5(c)、图5(d)表示MQHOA-A在优化2维Griewank函数时,尺度收缩过程中的三维波函数变化情况;图5(e)、图5(f)、图5(g)、图5(h)为对应的三维波函数平面投影。如图6(a)、图6(b)、图6(c)、图6(d)表示MQHOA-B在优化2维Griewank函数时,尺度收缩过程中的三维波函数变化情况;图6(e)、图6(f)、图6(g)、图6(h)为对应的三维波函数平面投影。 算法的波函数表示了函数可行解区域中最优解的概率分布,根据式(4),当xi和σs已知时,即可得到算法在当前尺度下的波函数,即目标函数自变量x的概率分布。 如图5所示,随着尺度的下降,MQHOA-A算法从高能态迅速下降到基态,算法在σs=0.625的尺度下迅速收敛到最优解位置附近,由于能级稳定判据的约束,算法能够较快地收敛至基态,从而获取目标函数的最优解。如图6所示,从图6(a)到图6(b)可以看出,MQHOA-B较MQHOA-A能级下降得较缓慢,在能级下降的初始阶段,跳出局部最优解的能力较弱。但是,在能级下降后期,MQHOA-B与MQHOA-A同样收敛到基态,获取目标函数的最优解。两个版本算法的波函数再一次印证了能级稳定判据的非必要性,虽然能级稳定判据能够在一定程度上加强算法从高能态下降到基态的能力,但是在无能级稳定判据约束的情况下,算法依然能够完成能级下降操作并收敛至目标函数的最优解位置。 4 结语 本文针对具有能级稳定判据的MQHOA提出了一种更加简洁的算法框架,新算法无能级稳定判据也能表现出较好的性能。通过实验分析,无能级稳定判据的算法在部分函数上的成功率和收敛情况均比有能级稳定判据的算法更加优异。无能级稳定判据的算法更加符合量子理论体系的物理模型,在算法的寻优过程中,可以认为每一次迭代都是算法向着能级较低的方向收敛,即向着目标函数最优解的方向移动。无能级稳定判据的算法结构更简单,实现更容易,可以更好地应用于实际问题的求解。在实际解决实际工程问题或者复杂问题时候,推荐使用更加简洁的MQHOA-B算法。 参考文献 [1]LAARHOVEN P J M, AARTS E H L. Simulated Annealing: Theory and Applications [M]. Dordrecht: Kluwer Academic Publishers, 1987: 16-48. [2]孙俊,方伟,吴小俊,等.量子行为粒子群优化:原理及其应用[M].北京:清华大学出版社,2011:19-30.(SUN J, FANG W, WU X J, et al. Quantum Behavior Particle Swarm Optimization: Principle and Its Application [M]. Beijing: Tsinghua University Press, 2011:19-30.) [3]王鹏,黄焱,李波,等.多尺度量子谐振子优化算法[M].北京:人民邮电出版社,2016:23-30.(WANG P, HUANG Y, LI B, et al. Multi-scale Quantum Harmonic Oscillator Optimization Algorithm [M]. Beijing: Posts and Telecom Press, 2016:23-30.) [4]WANG P, CHENG K, HUANG Y, et al. Multiscal quantum harmonic oscillator algorithm for multimodal optimization [J]. Computational Intelligence Neuroscience, 2018, 2018: Article No. 8430175. [5]WANG P, YE X, LI B, et al. Multi-scale quantum harmonic oscillator algorithm for global numerical optimization [J]. Applied Soft Computing, 2018, 69: 655-670. [6]王鵬,黄焱.具有能级稳定过程的MQHOA优化算法[J]. 通信学报,2016,37(7):79-86.(WANG P, HUANG Y. MQHOA optimization algorithm with energy level stabilization process [J]. Journal on Communications, 2016, 37(7): 79-86.) [7]韩虎,王鹏,程琨,等.基于多尺度量子谐振子算法的云计算任务调度[J].计算机应用,2017,37(7):1888-1892.(HAN H, WANG P, CHENG K, et al. Task scheduling algorithm for cloud computing based on multi-scale quantum harmonic oscillator algorithm [J]. Journal of Computer Applications, 2017, 37(7): 1888-1892.) [8]王梓懿,安俊秀,王鹏.基于多尺度量子谐振子算法的相空间概率聚类算法[J].计算机应用,2017,37(8):2218-2222.(WANG Z Y, AN J X, WANG P. Phase space probabilistic clustering algorithm based on multi-scale quantum harmonic oscillator algorithm [J]. Journal of Computer Applications, 2017, 37(8): 2218-2222.) [9]LI B, WANG P, JIN J. Multiscale quantum harmonic oscillator algorithm with strict metastability constraints for multi-modal optimization [J]. IEEE Access, 2019, 7: 17377-17388. [10]YE X, WANG P, XIN G, et al. Multi-scale quantum harmonic oscillator algorithm with truncated mean stabilization strategy for global numerical optimization problems [J]. IEEE Access, 2019, 7: 18926-18939. [11]王鹏,黄焱.多尺度量子谐振子优化算法物理模型[J].计算机科学与探索,2015,9(10):1271-1280.(WANG P, HUANG Y. Physical model of multiscale quantum harmonic oscillator optimization algorithm [J]. Journal of Frontiers of Computer Science and Technology, 2015, 9(10): 1271-1280.) This work is partially supported by the National Natural Science Foundation of China (60702075, 71673032), the Fundamental Research Funds for the Central Universities , Southwest Minzu University(2019NYB22). WANG Dezhi, born in 1992, M. S. candidate. His research interests incude parallel computing, quantum computing. WANG Peng, born in 1975, Ph. D., professor. His research interests include parallel computing, quantum computing.

