基于门限秘密共享的区块链分片存储模型

张国潮 王瑞锦

摘 要：针对存储原因所导致的区块链技术难以在大型业务场景应用的问题，提出了一种基于门限秘密共享的区块链分片存储模型。首先由共识节点使用改进的Shamir门限，将要上链的交易数据进行分片处理;其次，共识节点基于分片数据构造不同的区块，并分发给现存于区块链网络中的其他节点进行存储;最后，当节点要读取交易数据时，在从分发到交易数据分片的n个节点中的k个节点请求数据，并利用拉格朗日插值算法进行交易数据的恢复。实验结果表明，该模型在保证了上链数据安全性、可靠性、隐私性的同时，每个节点的数据存储量约为传统存储方法的1/（k-1），从而有利于区块链技术在大型业务场景的应用。

关键词：区块链存储;Shamir秘密共享;数据安全性;数据隐私性;分布式存储

中图分类号：TP309.2

文献标志码：A

Blockchain shard storage model based on threshold secret sharing

ZHANG Guochao， WANG Ruijin*

School of Information and Software Engineering， University of Electronic Science and Technology of China， Chengdu Sichuan 610054， China

Abstract：

To solve the problem that blockchain technology is difficult to be used in large-scale business scenarios due to storage constraints， a blockchain shard storage model based on threshold secret sharing was proposed. Firstly， the transaction data to be placed in blockchain was processed into shards by consensus nodes using improved Shamirs threshold secret sharing. Secondly， consensus nodes constructed different blocks based on data shards and distributed them to other nodes existing in the blockchain network for storage. Finally， when a node wanted to read transaction data， the node would request data from k of the n nodes with transaction data shards， and use Lagrange interpolation algorithm to recover the original transaction data. The experimental results show that the model not only guarantees the security， reliability and privacy of data to be placed in blockchain， but also effectively reduces the amount of data stored by each node to 1/（k-1）， which is conducive to blockchain technology using in large-scale business scenarios.

Key words：

storage in blockchain; Shamirs secret sharing; data security; data privacy; distributed storage

0 引言

2008年，文章《比特幣：一种点对点电子现金系统》[1]的发表，标志着区块链技术的出现。就技术层次进行分析，区块链属于一种技术组合，它对数据的存储依赖于相关区块结构。同时，利用技术体系，即密码学知识、点对点（Peer-to-Peer， P2P）网络架构、共识算法等机制对数据可靠传输、存储、以及访问等进行保障，并使多方协同参与和维护。得益于其能够在无需相互信任的节点间建立一个可信任的分布式系统，实现数据的不可篡改且可溯源等特点，目前区块链技术已越来越被广泛关注并应用到各行各业中。

然而，现如今区块链技术仍然有许多的缺陷和漏洞，存储问题就是其中需要解决的主要问题之一。就比如比特币系统，到2018年10月18日，比特币一共产生了546349个区块，区块的大小一般为996.2KB，整个完整区块链的大小为186.9GB[2]。而现如今比特币全节点（保存完整区块链信息的节点）的数量已上升到1万多个[3]，可以计算得到这1万多个全节点用了约2000TB的存储容量存储了200GB左右的数据。一方面对于每个节点，整个完整区块链的容量大小已达几百GB;另一方面对于整个区块链网络，所需存储空间与区块链的容量大小相差巨大，这使得存储空间被极大地消耗和浪费。而且数据量以及节点数量将会随着时间的推移越来越多，整条区块链的存储大小以及整个区块链网络所需的存储空间也将会越来越大，这也是目前区块链技术难以在数据量较大的业务场景应用的主要原因之一。

为了减小每个节点所需存储的完整区块链大小，让区块链技术能够在大型业务场景得到较好的应用，本文提出了一种基于门限秘密共享的区块链分片存储模型帮助改进区块链的存储问题。

本文的主要贡献如下：

1）提出了一种基于门限秘密共享的区块链分片存储模型。该模型将要上链的交易数据数字化后，分片存储于各个节点中，并不需要将完整的交易数据都存储到每个节点中。在保证数据安全可靠的条件下，使得每个节点需要消耗的存储空间减少。

2）通过实验表明，基于门限秘密共享的区块链分片存储模型在保障了数据安全性、隐私性、可靠性的同时，又能够有效减少每个节点所需存储的数据量，从而有利于区块链技术在大型业务场景的应用。

1 相关工作

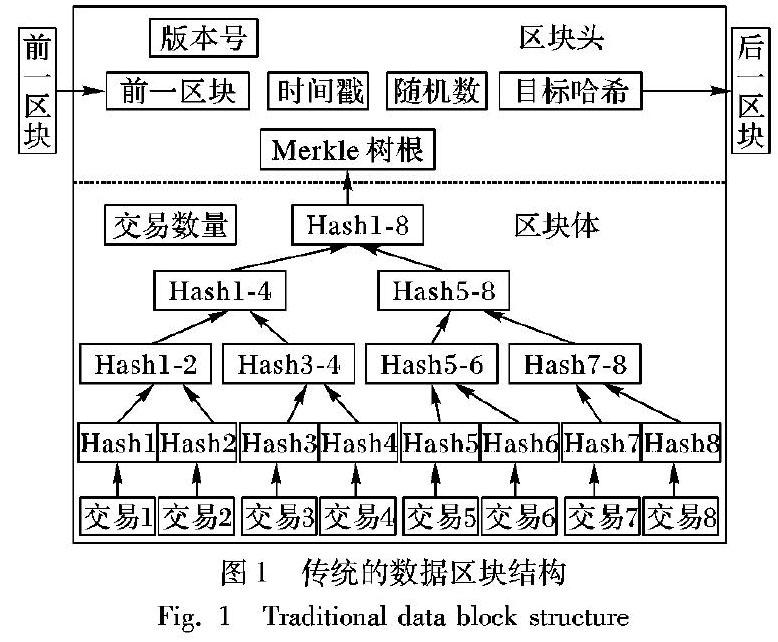
区块链是分布式的，它是一个公开的账本。参与共识的节点通过执行工作量证明（Proof of Work， PoW）协议来获得往账本写入数据的权利。PoW协议规定节点需要找出一个满足一定难度要求的随机数，最先找出该随机数的节点获得记账权并向全网广播本轮需要写入区块链的数据，当被其他节点进行验证并通过后，它们将一起存储数据，达成共识。每个节点每轮所存储的数据区块是一样的，如图1所示。

按照时间的顺序，区块链将各个数据区块进行链接。在每个数据区块中，都存在两个结构——区块头与区块体[4]。其中，当前的版本号、前一区块的地址、当前区块的目标哈希值、当前区块PoW共识的随机数解Nonce、Merkle树根以及时间戳等信息存在于区块头中。而对当前交易数量以及区块生成过程中，经过验证的所有交易数据的进行封装了的结构则是区块体。这些交易数据通过进行不断的迭代哈希，直到最后一个哈希值为止，并将结果作为Merkle树的树根记录到区块头中。最终每个节点都存储有整个区块链网络中最长区块链的一份拷贝，如图2所示，可以看见整个区块链网络的存储架构。

近年来，越来越多的学者从事区块链的研究工作。2016年，Dennis等[5]提出了一种时间“滚动”区块链，在不影响区块链安全的前提下能够解决当前区块链指数增长的问题，为区块链的可伸缩性提供了一种可行的处理方式。Wu等[6]在2007年基于能源网络提出了一种新的混合区块链存储模式，该存储模式能够提高整个能源网络在大数据量存储下的运行效率。Raman等[7]提出了用于扩展区块链的动态分布式存储方案，该存储方案能够降低区块链存储成本以及工作量证明所需消耗的能源成本。2018年，Lind等[8]构造了Teechain，可以通过线下支付渠道来降低区块链上的存储成本，使得区块链性能显著改进。zyilmaz等[9]通过采用分区未花费的交易输出（Unspent Transaction Output， UTXO）空间和拆分区块链的方法，来提高区块链的事务吞吐量。Dai等[10]提出了一个 NC-DS（Network Coded Distributed Storage）框架来存储区块链，该框架应用到区块链中能够显著减少所需的存储空间。

2 基于门限秘密共享的区块链分片存储模型

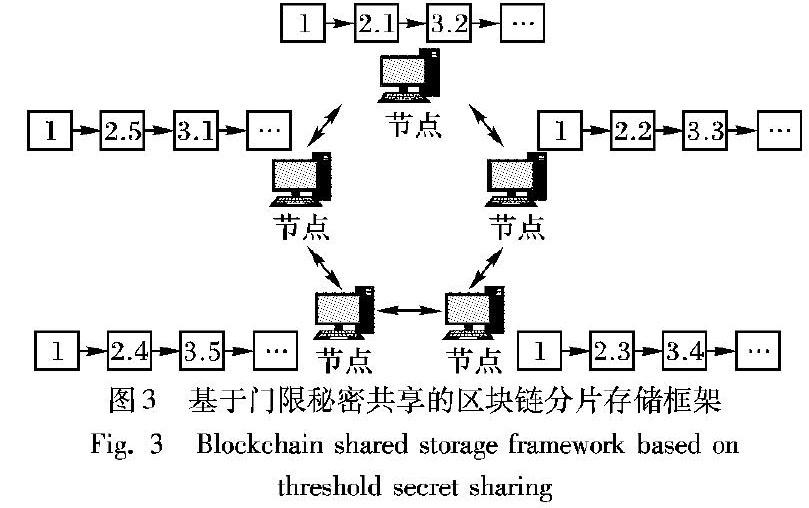
本文提出了一种基于门限秘密共享的区块链分片存储模型，利用了改进后的Shamir门限秘密共享方案[11]。核心思想是将交易数据数字化后，利用改进的Shamir门限秘密共享原理构造出k-1次多项式，并从中取出n个分片数据构造n种类型的数据区块，将这n个数据区块分布存储于区块链网络中。当要进行数据读取时，再从其中的k个节点获取分片数据，利用拉格朗日插值算法迭代恢复出交易数据。基于门限秘密共享的区块链分片存储模型的存储框架如图3所示。

基于門限秘密共享的区块链分片存储模型中的节点，主要有三种类型的角色：分片/广播节点、存储/验证节点以及其他节点，其中分片/广播节点与存储/验证节点的数量为n个。如图4所示，分片/广播节点是获得记账权的节点，该节点需要将本轮要记录到区块链上的交易数据进行n分片并构造n个数据区块来存储这n个分片，之后将其中的n-1个区块分发给区块链网络中的n-1个存储/验证节点。存储/验证节点是收到数据区块的节点，首先需要对数据区块的正确性进行验证，之后再链接数据区块。其他节点则是除去这n个节点外的共识节点，需要向邻近的这n个节点集合中的一个请求数据区块，或者接收它们广播的数据区块并链接到区块链上。

与传统利用Merkle树进行存储的数据区块结构不同的是，在本模型中，由于交易数据被分片存储于n个不同的区块中，所以数据区块结构有所变化，如图5所示。本模型的数据区块结构与传统的数据区块结构主要区别在于区块体部分以及区块头存放的哈希值。区块体主要由交易数据哈希值、交易数量、分发节点地址、分片大小、门限参数、分片编号、分片数据、填充等组成。交易数据哈希值是为了保证交易数据的完整性、填充字段是为了保证每个节点存储的分片数据大小一致而设置的。其中的交易数据哈希值、交易数量、分发节点地址、分片大小、门限参数在每个分发给存储/验证节点的区块中都是一样的，所以通过哈希得到的最终的Merkle树根也是一样的。即对于每个节点其区块头部分是一样的，这样就不影响每个节点的工作量证明。又因为分发给每个节点的区块是不一样的（区块体的差异），所以原先存放在区块头中前一区块的哈希值将变为前一区块的区块头的哈希值。

2.1 数据存储

基于门限秘密共享的区块链分片存储模型在进行数据存储时需要经历4个阶段：分片数据产生阶段、数据区块构造阶段、数据区块分发阶段、数据区块存储阶段。该算法的输入为本轮要上链的交易数据T′，输出为存储/验证节点将分配的数据区块链接到区块链上。数据存储算法基本步骤如下所示：

1）分片数据产生阶段。

① 将交易数据T′字符串化后，再转为十进制数字T;

② 根据此时的区块链网络状态设定门限参数（k，n），其中k

③ 将十进制数字T分成k-1份，即T = d1|d2|…|dk-1;

④ 利用改进Shamir门限秘密共享构造k-1次多项式Fk-1（x）;

a）选取一个大素数p，使得p > max（dmax，n），其中dmax=max（di），1≤i≤k-1（由于dmax 一般会较大，所以若在区块中存储p值需要较大的存储空间，故一般建议p取较大的固定值，如219937–1（6002位）、244497-1（13395位）、277232917-1（23249425位）等）;

b）在区域 Zp中随机选取一个数a生成曲线F1（x）= ax + d1;

c）在生成的曲线上选取两个点Ad11=F1（1）和Ad12=F1（2）;

d）Do for 2≤i≤k-1

A）用前面生成的点和di生成多项式曲线：

Fi（x）=Adi-1（i）*xi+Adi-1（i-1）*xi-1+…+Adi-11*x+di

B.1）当i ！= k-1时，在此曲线上选取i+1个点作为秘密共享并删除前一次生成的秘密共享;

B.2）当i = k-1时，输出k-1次多项式：

Fk-1（x）=Adk-2（k-1）*xk-1 + Adk-2（k-2）*xk-2 +…+ Adk-21*x + dk-1

⑤ 从步骤④得到的k-1次多项式中选取n个点，即T1 =[1， Fk-1（1）]、T2 = [2， Fk-1（2）]、…、Tn =[n， Fk-1（n）]作为n个分片数据。

2）数据区块构造阶段。

⑥ 根据区块结构计算所需的相关参数值及其哈希值，并选定n个存储/验证节点（分片/广播节点是其中的一个存储/验证节点）;

⑦ 根据已有的数据参数及分片数据构造n个数据区块;

3）数据区块分发阶段。

⑧ 将n个数据区块分发给选定的n个存储/验证节点;

4）数据区块存储阶段。

⑨ 存储/验证节点检验区块的正确性。主要有以下几个需要检验：

a）计算前一区块头的哈希值与该区块头中存放的哈希值是否一致;

b）该区块的工作量证明是否正确;

c）该区块的结构是否正确;

d）……

⑩ 当检验结果无误时，存储/验证节点将分配的数据区块链接到区块链上。

2.2 数据读取

基于门限秘密共享的区块链分片存储模型在进行数据存储时需要经历两个阶段：分片数据获取阶段、分片数据拼接阶段。该算法的输入为要读取区块信息的位置索引index （如index=1，即表示创世区块），输出为指定位置区块的信息（相关参数信息、交易数据信息等）。数据读取算法基本步骤如下所示：

1）分片数据获取阶段。

① 共识节点根据index值，查看自己区块链上对应的区块;

② 获取该区块上记录的分发节点地址信息、门限参数（k，n）信息等;

③ 根据分发节点地址信息，依次向分发节点请求index数据区块的分片数据，直到获得k个分片数据为止（包括自身存储的一个）;

2）分片数据拼接阶段。

④经过步骤①～③，此时共识节点一共有k个分片数据，不妨假设为T1=[1， Fk-1（1）]、T2=[2， Fk-1（2）]、…、Tk = [k， Fk-1（k）]，利用拉格朗日插值算法，如式（1）、（2）所示：

f（x）=∑ki=1f（xi）∏kj=1 j≠ix-xjxi-xj（1）

d=f（0）=∑ki=1f（xi）∏kj=1 j≠i-xjxi-xj mod p（2）

可以求得k-1次多项式Fk-1（x）并获得分片数据dk-1;

⑤ 从步骤④得到的Fk-1（x）中提取系数Adk-2（k-1）、Adk-2（k-2）、…、Adk-21， 即[1， Fk-2（1）]、[2， Fk-2（2）]、…、[k-1，Fk-2（k-1）]。根据步骤④，再次利用拉格朗日插值算法可求得k-2次多项式Fk-2（x）并获得数据分片dk-2;

⑥ 重复执行步骤④和步骤⑤，直到获得全部的数据分片dk-1、dk-2、…、d1;

⑦ 按照d1至dk-1的顺序将分片数据拼接为十进制数字T，即d1|d2|…|dk-1 = T;

⑧ 将十进制数字T字符串化后转为交易数据T′;

⑨ 将交易数据T′以及该区块的其他相关参数信息输出。

2.3 模型优缺点分析

基于门限秘密共享的区块链分片存储模型，利用改进的Shamir门限秘密共享将交易数据分片存储于n个不同的区块中，并分发给n个不同的共识节点。当要进行数据读取时，在从其中的k个节点请求数据进行数据的恢复。该模型的主要优点在于：

1）数据安全性有效保障。虽然本文改进了传统的区块链存储模型，但是上链数据的安全性并未受到影响。本小节同样以比特币为例，分叉攻击（51%攻击）是针对基于工作量证明共识算法的最出名的一种攻击方式，其主要目的在于实现“双花”。对于该攻击方法，中本聪在文献[1]中已给出证明，恶意攻击者要追赶上诚实节点实现“双花”的概率为：

1-∑zi=0λie-λi！1-qpz-i（3）

其中：λ=zq/p; p为诚实节点在一轮竞争中领先的概率，q为攻击者在一轮竞争中领先的概率，假定p>q; z为诚实节点领先的区块数。从式（3）中可以看出，恶意攻击者攻击成功的概率随着区块数z的增加而呈指数化下降。即攻击成功与否主要与各节点的算力大小有关（算力的大小与p、q正相关），与区块链所使用的存储模型并没有太直接的关系，所以上鏈数据的安全性依旧可以得到保障。另一方面，由于交易数据被数字化分片存储，每个节点存储的数据是相对没有意义的数值，即使恶意攻击者获得了某些节点存储的数据，也难以恢复出初始的交易数据。要想查看交易数据，仅能通过合法的方式向节点发出读取交易数据的请求。即从某种意义上来说，交易数据的隐私性保护得到提升。

2）数据的可靠性有效提高。相较于传统的数据分片需要分到数据的n个共识节点同时在线才能恢复出原始的数据，本模型仅需分到数据的n个共识节点中有k个节点在线即可进行数据的恢复。

3）共识节点所需存储空间显著减少。对比于传统的Shamir门限秘密共享中秘密共享大小与原来的秘密大小一样，本模型利用改进Shamir门限秘密共享能够使得秘密共享大小仅为原来秘密的1/（k-1），从而在数据存储过程中，每个共识节点所需存储交易数据的大小仅为原来的1/（k-1）。

该模型本质上采用的是一种以时间换空间的思想。虽然在存储空间上，共识节点所需的存储空间大小能够有效减少，但是在整个区块链网络运行过程中，节点的计算开销与通信开销将会增加。尽管如此，该模型在以数据上链需求为主的大型业务场景中將能得到较好的应用。

3 实验结果与分析

本实验是在PC配置为Intel Core i5-7300HQ 2.50GHz CPU和8GB内存上进行的。通过开启不同的服务器端口在本地创建不同的共识节点，每个共识节点均运行着自己搭建的区块链代码。实验中一共建立了10个节点，所有节点均为存储/验证节点，且其中一个同时是分片/广播节点。当每提交10笔交易后，本实验进行一次挖矿，即每个区块中（除创世区块）存储了10笔交易数据，且每笔交易数据都是一样的，以此确保每次要上链的数据大小一致。最后，实验中的门限参数为k=5，n=10，大素数q取固定值219937 - 1。

由于本文只关注区块链的存储问题，所以在实验中简化了工作量证明，即共识节点仅需将前一区块的工作量证明值与当前区块的工作量证明值进行拼接，之后计算哈希值，若哈希值的前5位是0则完成工作量证明（采用该种工作量证明，由于创世区块工作量证明值是设置固定的一个值，所以在不考虑其他影响因素条件下，每次运行区块链产生每个对应编号区块，所需的时间是一样的）。

首先测试基于Merkle树的传统区块链存储模型与基于门限秘密共享的区块链分片存储模型，对于每个区块产生时间，即数据存储时间的差异。本实验一共产生了200个区块，并记录了每个节点从接收到第10笔交易开始到将交易数据上链的时间。在所有节点都正常运行且不被攻击的情况下，得到如图6所示结果。

分析图6（a）、（b）的实验结果可以知道，两种存储模型在每个区块产生时间上的差异并不是很大，基于Merkle树的传统区块链存储模型的平均区块产生时间为3.326s，而基于门限秘密共享的区块链分片存储模型的平均区块产生时间为3.382s。这主要是因为在区块构建过程中，传统的方法需要构建Merkle树，本模型需要产生数据分片来构建每个共识节点的区块，所以基于门限秘密共享的区块链分片存储模型的平均区块生成时间并没有比传统的方法多多少。

其次测试基于Merkle树的传统区块链存储模型与基于门限秘密共享的区块链分片存储模型，对于获取区块上的数据所花费的时间，即数据读取时间的差异。在产生的200个区块基础上，分别记录读取编号为5的倍数的区块数据所花费的时间。在所有节点都正常运行且不被攻击的情况下，得到如图7所示结果。

分析图7（a）、（b）的实验结果可以知道，基于Merkle树的传统区块链存储模型的平均区块数据读取时间为0.020s，而基于门限秘密共享的区块链分片存储模型的平均区块读取时间为0.087s。可见，在数据读取方面，本模型的读取时间会比传统的方法长。这是由于当进行数据读取时，本模型需要从其他分到分片数据的节点请求数据，之后还要运用拉格朗日插值算法进行数据的恢复，相比于传统的方法，通信开销与计算开销将会增加，所以数据读取会慢一点。

最后测试基于Merkle树的传统区块链存储模型与基于门限秘密共享的区块链分片存储模型，在区块产生过程中，每个节点所花费存储空间的差异。实验中一共产生了200个区块，当每产生5个区块时，将此时的完整区块链写入文件中，并记录文件大小，从而获得每个节点所花费的存储空间大小。在所有节点都正常运行且不被攻击的情况下，得到如图8所示结果。

分析图8的实验结果可以知道，一方面，在两种存储模型中，随着区块加入到区块链，节点所需的存储空间几乎呈线性增长。这主要是因为本实验固定了每个区块所存储交易数据的大小，所以才会出现图形几乎呈线性的形状。另一方面，从图10中可以观察到，随着区块不断地加入区块链中，基于Merkle树的传统区块链存储模型的节点所需的存储空间，几乎是基于门限秘密共享的区块链分片存储模型的节点的3.3倍。可见，本模型对于区块链存储问题的解决具有显著的效果。实验过程中的门限参数取值为k=5，n=10，理论上，基于本模型的每个节点所需存储的分片数据大小，是传统方法中整个数据大小的1/（k-1）倍，之所以实验结果略大于该值（13.3>14），是因为在构建区块过程中，本模型需要在区块中加入一些其他的字段信息，比如分发节点地址、门限参数等。

4 结语

本文首先讲述了目前困扰区块链技术广泛应用的主要问题之一的存储问题。之后提出了基于门限秘密共享的区块链分片存储模型，该模型利用改进Shamir门限秘密共享将交易数据n分片并构造n个不同的区块分别存储于n个不同的存储/验证节点;当要进行数据恢复时，再从其中的k个节点请求分片数据，即可进行数据的恢复。最后，经实验证明，基于门限秘密共享的区块链分片存储模型在保障了数据安全性、隐私性、可靠性的同时，又能够有效减少每个节点所需存储的数据量，从而有利于区块链技术在大型业务场景的应用。本文的一些细节还可以进一步研究，如门限k取多大值才合适，要采用什么样的方法将交易数据转化为十进制数字等。下一步将继续研究，以便区块链中的相关存储限制问题能够更完善地被解决。

参考文献

[1]NAKAMOTO S. Bitcoin： a peer-to-peer electronic cash system [EB/OL]. [2018-10-18]. https：//bitcoin.org/bitcoin.pdf.

[2]Blockchain. The blockchain data of Bitcoin [EB/OL]. [2018-10-18]. https：//www.blockchain.com.

[3]Bitnodes. The bitnodes data of Bitcion [EB/OL]. [2018-10-18]. https：//bitnodes.earn.com.

[4]袁勇，王飛跃. 区块链技术发展现状与展望[J].自动化学报，2016，42（4）：481-494.（YUAN Y， WANG F Y. Blockchain： the state of the art and future trends [J]. Acta Automatica Sinica， 2016， 42（4）： 481-494.）

[5]DENNIS R， OWENSON G， AZIZ B. A temporal blockchain： a formal analysis[C]// Proceedings of the 2016 International Conference on Collaboration Technologies and Systems. Piscataway， NJ： IEEE， 2016： 430-437.

[6]WU L， MENG K， XU S， et al. Democratic centralism： a hybrid blockchain architecture and its applications in energy Internet [C]// Proceedings of the 2016 International Conference on Energy Internet. Piscataway， NJ： IEEE， 2017： 176-181.

[7]RAMAN R K， VARSHNEY L R. Dynamic distributed storage for scaling blockchains [EB/OL]. [2018-10-18]. https：//arxiv.org/pdf/1711.07617.pdf.

[8]LIND J， NAOR O， EYAL I， et al. Teechain： reducing storage costs on the blockchain with offline payment channels [C]// Proceedings of the 11th ACM International Systems and Storage Conference. New York： ACM， 2018： 125.

[9]ZYILMAZ K R， PATEL H， MALIK A. Split-scale： scaling bitcoin by partitioning the UTXO space[C]// Proceedings of the IEEE 9th International Conference on Software Engineering and Service Science. Piscataway， NJ： IEEE， 2018： 41-45.

[10]DAI M， ZHANG S， WANG H， et al. A low storage room requirement framework for distributed ledger in blockchain [J]. IEEE Access， 2018， 6： 22970-22975.

[11]王学军.无线传感器网络中分布式存储方案的改进[J].网络安全技术与应用，2012（7）：5-7.（WANG X J. Improvement in distributed data storage scheme for wireless sensor networks [J]. Network Security Technology and Application， 2012（7）： 5-7.）

[12]KOSBA A， MILLER A， SHI E， et al. Hawk： the blockchain model of cryptography and privacy-preserving smart contracts [C]// Proceedings of the 2016 IEEE Symposium on Security and Privacy. Piscataway， NJ： IEEE， 2016： 839-858.

[13]ATENIESE G， MAGRI B， VENTURI D， et al. Redactable blockchain-or-rewriting history in bitcoin and friends [C]// Proceedings of the 2017 IEEE European Symposium on Security and Privacy. Piscataway， NJ： IEEE， 2017： 111-126.

[14]CAI C， YUAN X， WANG C. Towards trustworthy and private keyword search in encrypted decentralized storage [C]// Proceedings of the 2017 IEEE International Conference on Communications. Piscataway， NJ： IEEE， 2017： 1-7.

[15]HALPIN H， PIEKARSKA M. Introduction to security and privacy on the blockchain [C]// Proceedings of the 2017 IEEE European Symposium on Security and Privacy Workshops. Piscataway， NJ： IEEE， 2017： 1-3.

[16]FUKUMITSU M， HASEGAWA S， IWAZAKI J， et al. A proposal of a secure P2P-type storage scheme by using the secret sharing and the blockchain [C]// Proceeddings of the IEEE 31st International Conference on Advanced Information Networking and Applications. Piscataway， NJ： IEEE， 2017： 803-810.

[17]XU C， WANG K， XU G， et al. Making big data open in collaborative edges： a blockchain-based framework with reduced resource requirements [C]// Proceeddings of the 2018 IEEE International Conference on Communications. Piscataway， NJ： IEEE， 2018： 1-6.

[18]LEWISON K， CORELLA F. Backing rich credentials with a blockchain PKI [EB/OL]. [2018-10-18]. https：//pomcor.com/techreports/BlockchainPKI.pdf.

[19]LI Y， ZHENG K， YAN Y， et al. EtherQL： a query layer for blockchain system [C]// Proceeddings of the 2017 International Conference on Database Systems for Advanced Applications， LNCS 10178. Berlin： Springer， 2017： 556-567.

[20]LI Y， HUANG J， QIN S， et al. Big data model of security sharing based on blockchain [C]// Proceeddings of the 3rd International Conference on Big Data Computing and Communications. Piscataway， NJ： IEEE， 2017： 117-121.

This work is partially supported by the National Natural Science Foundation of China （61802033）.

ZHANG Guochao， born in 1998. His research interests include blockchain， network security.

WANG Ruijin， born in 1980， Ph. D.， associate professor. His research interests include information system security， quantum communication security， cloud security.