改进SMOTE的不平衡数据集成分类算法

王忠震 黄勃 方志军 高永彬 张娟

摘 要：針对不平衡数据集的低分类准确性，提出基于改进合成少数类过采样技术（SMOTE）和AdaBoost算法相结合的不平衡数据分类算法（KSMOTE-AdaBoost）。首先，根据K近邻（KNN）的思想，提出噪声样本识别算法，通过样本的K个近邻中所包含的异类样本数目，对样本集中的噪声样本进行精确识别并予以滤除;其次，在过采样过程中基于聚类的思想将样本集划分为不同的子簇，根据子簇的簇心及其所包含的样本数目，在簇内样本与簇心之间进行新样本的合成操作。在样本合成过程中充分考虑类间和类内数据不平衡性，对样本及时修正以保证合成样本质量，平衡样本信息;最后，利用AdaBoost算法的优势，采用决策树作为基分类器，对平衡后的样本集进行训练，迭代多次直到满足终止条件，得到最终分类模型。选择G-mean、AUC作为评价指标，通过在6组KEEL数据集进行对比实验。实验结果表明，所提的过采样算法与经典的过采样算法SMOTE、自适应综合过采样技术（ADASYN）相比，G-means和AUC在4组中有3组最高;所提分类模型与现有的不平衡分类模型SMOTE-Boost，CUS-Boost，RUS-Boost相比，6组数据中：G-means均高于CUS-Boost和RUS-Boost，有3组低于SMOTE-Boost;AUC均高于SMOTE-Boost和RUS-Boost，有1组低于CUS-Boost。验证了所提的KSMOTE-AdaBoost具有更好的分类效果，且模型泛化性能更高。

关键词：不平衡数据分类;合成少数类过采样技术;K近邻;过采样;聚类;AdaBoost算法

中图分类号：TP181

文献标志码：A

Improved SMOTE unbalanced data integration classification algorithm

WANG Zhongzhen1， HUANG Bo1，2*， FANG Zhijun1， GAO Yongbin1， ZHANG Juan1

1.School of Electric and Electronic Engineering， Shanghai University of Engineering Science， Shanghai 201620， China;

2.Jiangxi Province Economic Crime Investigation and Prevention and Control Technology Collaborative Innovation Center， Nanchang Jiangxi 330103， China

Abstract：

Aiming at the low classification accuracy of unbalanced datasets， an unbalanced data classification algorithm based on improved SMOTE （Synthetic Minority Oversampling TEchnique） and AdaBoost algorithm （KSMOTE-AdaBoost） was proposed. Firstly， a noise sample identification algorithm was proposed according to the idea of K-Nearest Neighbors （KNN）. The noise samples in the sample set were accurately identified and filtered out by the number of heterogeneous samples included in the K neighbors of the sample. Secondly， in the process of oversampling， the sample set was divided into different sub-clusters based on the idea of clustering. According to the cluster center of the sub-cluster and the number of samples the sub-cluster contains， the synthesis of new samples was performed between the samples in the cluster and the cluster center. In the process of sample synthesis， the data imbalance between classes as well as in the class was fully considered， and the samples were corrected in time to ensure the quality of the synthesized samples and balance the sample information. Finally， using the advantage of AdaBoost algorithm， the decision tree was used as the base classifier and the balanced sample set was trained and iterated several times until the termination condition was satisfied， and the final classification model was obtained. The comparative experiments were carried out on 6 KEEL datasets with G-mean and AUC selected as evaluation indicators.

The experimental results show that compared with the classical oversampling algorithm SMOTE and ADASYN （ADAptive SYNthetic sampling approach）， G-means and AUC have the highest of 3 groups in 4 groups.

Compared with the existing unbalanced classification models SMOTE-Boost， CUS （Cluster-based Under-Sampling）-Boost and RUS （Random Under-Sampling）-Boost， among the 6 groups of data： the proposed classification model has higher G-means than CUS-Boost and RUS-Boost， and 3 groups are lower than SMOTE-Boost; AUC is higher than SMOTE-Boost and RUS-Boost， and one group is lower than CUS-Boost.

It is verified that the proposed KSMOTE-AdaBoost has better classification effect and the model has higher generalization performance.

Key words：

unbalanced data classification; Synthetic Minority Oversampling TEchnique （SMOTE）; K-Nearest Neighbors （KNN）; oversampling; clustering; AdaBoost algorithm

0 引言

不平衡數据集是指数据集中某个或某些类样本数量远远高于其他类，反之则样本数量低于其他类，通常把样本数量较多的类称为多数类，样本数量较少的类称为少数类[1]。在不平衡数据集中，少数类样本所包含的信息有可能更加关键，例如医疗诊断[2]中人类患恶性疾病的事件属于少数类，但是如果将恶性疾病诊断为良性，就会错过最佳的治疗时机，严重影响身体健康。不平衡分类问题是指：由于不平衡数据集本身数据分布的不平衡性，使用传统分类算法的效果较差，模型准确度较低。随着大数据时代的到来，现在这种问题普遍存在于故障检测[3]、信用卡欺诈检测[4]、网络入侵识别[5]以及电子邮件分类[6]等领域，对不平衡数据集进行科学的分类已经成为学术研究的一个热点。

针对不平衡数据集的分类研究，目前的处理方法主要分为三类：数据层面的方法、算法层面的方法以及数据与算法层面相结合的方法。数据层面的方法，目前方法是使用欠采样和过采样两种方式，即对数据集中多数类样本进行删除或对少数类样本进行增加以达到平衡数据集的目的;代表性的算法有合成少数类过采样技术（Synthetic Minority Oversampling Technique， SMOTE）[7]、自适应综合过采样技术（ADAptive SYNthetic sampling approach， ADASYN）[8]、Borderliner-SMOTE算法[9]。算法层面的方法，现有算法绝大多数是在平衡数据分类算法的基础上，通过引入损失函数或者错误率进行改进;代表性的算法有代价敏感学习[10]、集成学习[11]和提升算法[12]。融合数据采样与分类算法的方法，使其训练得出的分类器具有更强的多元性和鲁棒性：文献[13]提出了在自适应增强（Adaptive Boosting， AdaBoost）每次迭代中对多数类样本进行随机欠采样（Random Under-Sampling， RUS）的RUSBoost算法，由于随机采样方法的不确定性，往往一些采样出来的样本不具有代表性，对模型效果的提升不明确;文献[14]提出以一种基于SMOTE算法和AdaBoost.M2算法相结合的不平衡数据集分类算法，该算法虽然在一定程度上提高了分类器的召回率和预测的准确度，但并没有考虑到少数类样本中的边缘化问题以及存在噪声样本干扰问题。

本文提出一种针对不平衡数据二分类问题的KSMOTE-自适应增强（KSMOTE-AdaBoost）算法。首先针对少数类样本中存在的噪声样本干扰问题，引入K-最近邻（K-Nearest Neighbors， KNN）噪声样本滤除算法，对噪声样本进行滤除。其次考虑现有过采样方法的合成样本不具有代表性、忽略同类样本之间的差异性问题，依据机器学习中的聚类思想，对现有的过采样算法进行改进，引入子簇质心、过采样权重等概念，对合成样本进行修正，提高整体合成样本的质量;最后将过采样后的数据集使用以决策树（Decision Tree， DT）作为基分类器的AdaBoost算法进行分类。通过将本文提出采样算法与经典的SMOTE、ADASYN采样算法相对比，本文的分类模型与于聚类的提升欠采样的非平衡数据分类（Cluster-based Under-Sampling with Boosting for imbalanced classification， CUS-Boost）等三种分类模型相对比，实验表明本文采样算法采样后的样本更具有代表性，本文的分类模型具有更好的分类效果，验证了本文方法的有效性与可行性。

1 预备理论

1.1 SMOTE算法

Chawla[7]在2002年提出了少数类样本合成技术，即SMOTE。该算法的特点是：通过在少数类样本与其K个最近邻样本之间线性内插的方法合成新的样本，其合成公式如下：

Xnew=Xi+gif*（Xi， j-Xi）（1）

其中：Xnew为新少数类样本，Xi为第i个少数类样本，Xi， j为第i个少数类样本的第j个近邻样本;gif∈[0，1]。

1.2 AdaBoost算法

AdaBoost算法是经典的Boosting算法，通过对弱分类器的组合来达到较好的预测效果。基本过程如下所示：首先给每个样本赋予同等的权重，例如有样本m个，每个样本的权重设置为1/m，以此样本分布为基础训练一个弱分类器。根据分类的结果，更新样本权重，对分类错误的样本增加其权重，相反则减少权重。在得到新的样本分布同时得出该弱分类器的权重。根据新的样本分布，进行新一轮的训练，更新样本权重，获得新的弱分类器与其权值，通过T次的迭代循环，将获得T个弱分类器与其权值。最后将T个弱分类器ft及其权值进行线性组合，得到最终强分类器。

算法的训练过程如下：

输入：训练样本集S={（X1，Y1），（X2，Y2），…，（Xi，Yi）}，i=1，2，…，n，Yi∈{1，0}，迭代次数T，基分类器为f;

输出：H（X）=sign（∑Tt=1αt ft（X））。

有序号的程序——————————Shift+Alt+Y

程序前

1）

初始化样本分布权重D1（i）=1/n，i=1，2，…，n

2）

For t=1 to T：

2.1） 根据样本分布Dt训练弱分类器ft： X → Y

2.2） 计算分类误差率et=∑ni=1Dt（i）I（ft（Xi）≠Yi），I是指示函数

2.3） 计算弱分类器的权重αt=12 ln 1-etet

2.4） 更新样本权值Dt+1（i）=Dt（i）Zt exp（-αtYift（Xi）），i=1，2，…，n，Zt=∑ni=1Dt（i）exp（-αtYi ft（Xi））为归一化因子

3）

End For

4）

H（X）=sign（∑Tt=1αtft（X））

5）

Return H（X）

程序后

2 KSMOTE-AdaBoost算法

本文提出的KSMOTE-AdaBoost分类模型分为3个部分：噪声样本滤除阶段、数据平衡阶段和数据训练分类阶段。分类模型如图1所示。

2.1 KNN噪声样本滤除算法

在真实数据集中，噪声数据的存在是不可避免的，并且在某种程度上会对分类器性能产生影响。尤其在少数类样本数量相对较少、样本抗干扰能力较弱的情况下，噪声数据对样本分布影响更大。所以本文在对少数类样本采样之前，引入KNN噪声样本滤除算法。该算法基于文献[16]中噪声样本识别算法，在类内以及类间样本的分布较为紧密的情况下，难以对噪声样本进行有效的识别与过滤的缺点。本文从提高合成样本质量、提升分类器模型性能出发，对噪声样本的定义如下：若某一少数类样本的K个近邻中超过2/3的样本为多数类样本，则将该样本定义为噪声样本。

KNN噪声样本滤除算法首先针对输入样本集，进行样本集的类别划分;然后通过K近邻算法获取每个少数类样本的近邻样本集，对各近邻样本集进行分类汇总;最后根据噪声样本判别条件对样本集中的噪声样本识别并滤除，详细的算法步骤如算法1所示。

算法1 KNN Noise Sample Removal。

输入：All datasets S; Number of nearest neighbors K;

輸出：New minority class dataset Sm′。

有序号的程序——————————Shift+Alt+Y

程序前

1）

S=SM∪Sm

Sm//Minority class dataset

SM//Majority class dataset

|Sm|// The number of minority class samples

Knn= NearestNeighbors（K）.fit（）//KNN algorithm

X_min=[ ]//Save the index of the security sample

2）

For i=1 to |Sm|：

2.1） S′=（Sm-Sm，i）∪SM

2.2） Knn= NearestNeighbors（K）.fit（S′）

2.3） Nnarray=Knn.kneighbors（Sm，i）//Calculate the K near neighbors of sample i in Sm from

//dataset S′ through the KNN algorithm，

//and save the indices in the Nnarray

2.4） Value，Counts=unique（S[Nnarray]）//S[] Select samples based on the index in the list.

//Count the number of majority and minority among K near //neighbors

2.5） if Counts[0]< K/3 or Value[0]==1：

2.5.1） X_min.extend[i]// Save the index of thei sample in the X_min

3）

End For

4）

Sm′=Sm[X_min]//New minority class dataset S′m

5）

Return Sm′

程序后

2.2 基于k-means改进的SMOTE算法

针对不平衡数据集中样本类别数目的不平衡性，文献[7-8]中提出的過采样算法，在进行样本采样时，更多考虑到样本类别之间的不平衡，即少数类与多数类之间的不平衡，没有充分地考虑同类样本本身分布的不平衡，即类间不平衡，以及合成样本分布“边缘化”问题。所以针对以上的问题，本文提出改进的SMOTE算法。

在分类任务中，不仅类间样本的不平衡性对模型性能造成影响，类内样本的不平衡性也同样影响。本文针对以上两类不平衡问题，引入子簇的概念。首先采用聚类算法k-均值聚类（k-means clustering， k-means）对样本集进行子簇的划分，根据子簇中样本数目为其分配不同的采样权重记作W（i），则有：

W（i）=1-num（i）/（∑ci=1num（i））（2）

其中：c表示样本集划分的类簇总数，num（i）表示第i个类簇中的样本数量。根据（2）可知，某一类簇中样本数目越多，则W（i）越小，即过采样权重越小，合成样本数目就越小，最终实现同类样本之间的平衡分布。

在过采样过程中，合成样本的质量越高，则模型的性能就越好;反之若合成样本分布在类别分布的“边缘”，则有可能影响多数类样本的分类精准度，且合成样本不具有代表性。为了防止新样本的“边缘化”，本文引入质心的概念，质心是指少数类划分子簇后每个子簇的簇心Ci，center。对SMOTE算法进行改进，原始的方法新样本的合成如（1）所示，改进后的公式如式（3）所示：

Xnew=Ci，center+gif*（Xi， j-Ci，center）（3）

其中：Ci，center表示第i个子簇的簇心，Xi， j表示第i个子簇中的第j个样本。整个公式表示为在Ci，center与Xi， j之间进行线性插值得到新的样本Xnew。

改进的SMOTE算法是根据样本集中所包含样本的分布特点，进行新样本的合成，合成过程如下：

1） 使用聚类算法将样本集划分为特定数目的类簇;

2） 根据需要合成样本的数目，以及各类簇中所包含样本数量，得出各类簇所占权重以及需要合成的样本数目;

3） 通过轮盘赌的方式进行样本的选择，在选中样本与所属类簇簇心之间进行线性插值，获得合成样本;

4） 输出合成样本集。

详细算法步骤如算法2所示。

算法2 Improved SMOTE。

输入：Sample set S;The number of synthetic new samples is Num; Number of clusters N;

输出：Synthestic sample set Snew。

有序号的程序——————————Shift+Alt+Y

程序前

1）

Snew=[]//array for synthetic samples

K=N//Number of clusters N

2）

kmeans=Kmeans（n_clusters=K）

3）

kmeans.fit（S）//Calculate the K class cluster of sample set S// through the k-means algorithm

4）

For j in range（kmeans.n_clusters）：

4.1）each_cluster={j：where（kmeans.labels_ == j）[0]}// Each sample is divided into different clusters

End For

5）

For i in each_cluster.keys（）：

5.1） Ci=S（i）

5.2） num（i）= unique（Ci）[1]// Calculate the number of samples in the i cluster

5.3） W（i）=1-num（i）∑ci=1num（i）

5.4） numnew（i）=Num*W（i）//The number of samples of the i cluster synthesis sample

5.5） Ci，center=kmeans.cluster_centers_[i]// The centroid of the i cluster

5.6） For j=1 to numnew（i）：

5.6.1） Xi， j=Random.choice（Ci，size=1）//Randomly select a sample from Ci

5.6.2） Snew.append（Xi， j）//Save the newly synthesized sample

End For

End for

6）

Return Snew

程序后

2.3 基于改进过采样的集成分类算法

数据集经过算法1和算法2处理后，会得到一个相对“干净”且平衡的数据集，最后对处理后的数据集使用AdaBoost算法训练分类模型。三者结合在一起，得出本文提出的KSMOTE-AdaBoost算法。

KSMOTE-AdaBoost算法训练过程如下：

1）通过算法1对样本集中噪声样本识别、滤除;

2）使用算法2对去噪后的样本集进行新样本的合成;

3）将合成的样本集与去噪后的样本集进行组合，获得平衡样本集;

4）对平衡样本集，通过AdaBoost算法进行模型训练;

5）获得KSMOTE-AdaBoost分类模型。

详细算法步骤如算法3所示。

算法3 KSMOTE-AdaBoost。

输入：Set S={（X1，Y1），（X2，Y2）…（Xi，Yi）}， i=1，2，…，n，Xi∈X， with labels Yi∈{0，1}，Number of iterations T， Base classifier f， Number of nearest neighbors K， Number of clusters k;

输出：H（X）=sign（∑Tt=1αtft（X））。

有序号的程序——————————Shift+Alt+Y

程序前

1）

Filter out noise samples in a small class of samples by Algorithm 1，get denoised sample set Sm′

2）

Synthesize a new minority sample set Snew by Algorithm

3）

Sall=Snew∪S

4）

Initialize the distribution D1（i）=1/（n+Num）;i=1，2，…，n，n+1，…，n+Num

5）

For t=1，2，…，T：

5.1） Train a weak learner using distribution Dt

5.2） Compute weak hypothesis ft：X×Y→[0，1]

5.3） Compute the pseudo-loss of hypothesis  ft： et=∑ni=1Dt（i）I（ft（Xi）≠Yi）

5.4） Set αt=12ln1-etet

5.5） Update Dt： Dt+1（i）=Dt（i）Ztexp（-αtYift（Xi））  where Zt is a normalization constant chosen such that Dt+1 is a distribution.

End for

6）

Return H（X）=sign（∑Tt=1αtft（X））

程序后

3 實验结果与分析

为验证本文所提出方法的具有较高的适用性，实验采用6组KEEL数据集，实验数据选择10次十折交叉验证后的平均值，作为对本文分类算法以及对比算法性能的评估标准。实验思路：首先选择类别不平衡数据集，对本文提出改进的过采样算法与以往算法进行比较，对比其实验结果，证明改进的过采样算法的有效性;然后将本文提出的分类模型与其他分类模型进行比较，验证本文的模型在处理不平衡数据上能够有更好的分类效果，更具有优势。

3.1 数据集

实验采用来自KEEL公开数据库中不同领域的6组数据集。这些数据集被国内大量的研究者引用。实验前要先对数据集进行预处理，同时把含有多类别的数据集划分为二分类别，预处理后的数据集特征如表1。

3.2 性能评价指标

针对不平衡数据集的特征，不能通过分类准确率的方式来评价一个分类模型的优劣，所以本文采用G-mean和AUC作为分类模型的评估指标（本文中定义少数类为正类，多数类为负类）。利用混淆矩阵表示不平衡数据的分类结果，见表2。

表格（有表名）

根据表2可求出如下评价指标：

少数类召回率（查全率）：

RP=TP/（TP+FN）（4）

多数类召回率（查全率）：

RN=TN/（TN+FP）（5）

G-mean=RP*RN（6）

AUC：在不平衡数据集分类器的评价标准中，“受试者工作特征”（Receiver Operating Characteristic， ROC）曲线是评价学习器泛化性能的有利工具。ROC曲线以FPTN+FP（假阳率）为横轴，以TPTP+FN（真阳率）为纵轴，给出的是当阈值变化时假阳率与真阳率的变化情况，阈值取自分类器的概率输出。最佳的分类器应该尽可能地处于左上角，这就意味着分类器在假阳率很低的同时获得了很高的真阳率。在进行分类器的比较时，若一个分类器的ROC 曲线被另一个分类器的曲线完全“包住”，则可断言后者的性能优于前者;若两个分类器的ROC曲线发生交叉，则难以一般性地断言两者孰优孰劣，所以引入ROC曲线下的面积进行对比，即AUC（Area Under Curve）[17]。

3.3 参数寻优

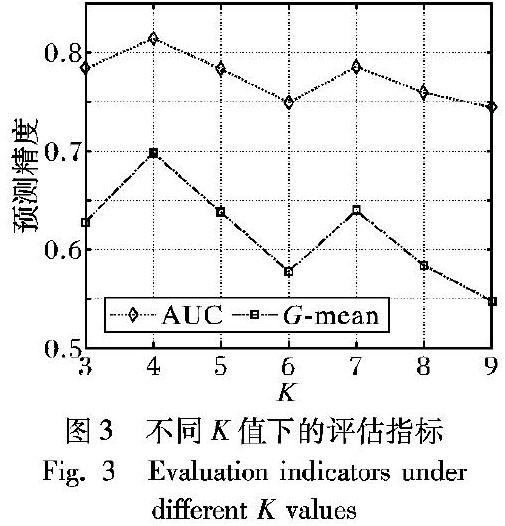
对于噪声处理阶段中KNN算法K的选取在本文中至关重要，因为K值的选取是确定某一样本是否为噪声的关键。若K值较小，则其样本中噪声样本难以过滤，分类器效果得不到提升;选取较大，会造成原有样本中信息数据的丢失，分类模型泛化性较低。对于K值的设定，本文通过将K值限定在3到9之间来进行参数寻优，并从两个方面考虑，一从噪声样本数量，对不用K值下每次过滤的噪声样本数量进行统计，取值为10次十折交叉后的平均值;二从评价指标G-mean值和AUC值，取值为同一K值下不同数据集10次十折交叉后的平均值。从图2与图3中可以看出，当K值取4时，其噪声样本的数量相对较小且平均G-mean、AUC取值最大。

对于聚类算法中K值的选取，本文自适应地调整各数据集K的取值，保证数据集聚类效果。方法如下：首先通过计算类中各点与类中心的距离平方和来度量类内的紧密度，再通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度，求二者比值，比值越大类与类之间越分散，即聚类结果更优。在实验中统一使用C4.5决策树算法作为所有实验的基本分类算法。根据表1中的数据可知，本文所选用数据集的不平衡率是存在差异的，所以其合成新样本的数目因不平衡率而不同。

3.4 本文过采样方法与其他过采样方法的比较

为验证本文所提出的样本合成算法的优势与降低数据集不平衡率的有效性，首先采用人工数据集进行验证，将本文样本合成方法与SMOTE算法进行对比，比较两者合成样本的分布情况。本文采用Python3.6中的Sklearn包随机生成两组高斯样本，样本数分别为35和50，合成样本数34。图4为不同算法合成样本分布对比效果图，所用数据为同一高斯分布数据集。

图4中原始少数类样本点用“×”符号表示，“●”符号表示合成少数类样本点。

图4（a）所示为原始少数类样本集分布情况，从图中可知样本集的分布主要聚集在两个区域，且每个区域中所包含样本数目不等。图4（b）所示为通过SMOTE采样后，所有样本的分布情况。与图4（a）相比，可以看出新合成样本中有较多样本分布在原始样本分布的“边缘”区域，且采样后的样本分布没有改变原样本集中的类内不平衡性。针对图4（b）中所呈现的不足，本文对SMOTE采样算法进行改进。在对样本集进行过采样之前，针对类内样本分布的不平衡性，引入子簇的概念，将样本集划分为不同的子簇，并通过式（2）赋予其不同的采样权重。针对合成样本的“边缘性”问题，引入簇心的概念。将簇心与任一簇内样本进行线性组合，通过式（3）合成新样本，实验效果图如图4（c）所示。

其次为验证本文所提出的过采样方法的泛化性，使用本文的方法与SMOTE、ADASYN在不同数据集上对G-mean和AUC评价指标进行对比。实验中均采用scikit-learn自带的C4.5作为分类器。实验结果如表3所示（加粗部分为最好实验结果）。

由表3实验数据可以看出本文提出的过采样算法确实提高了预测效果。在数据集Glass1和Yeass6上G-mean和AUC表现均高于其他方法，G-mean值最高提高了2.1%，AUC值提高了4.6%;对比经典的过采样算法SMOTE，G-mean值平均提高了约1.8%，AUC值平均提高了约2.6%;

由表3实验数据可以看出本文提出的过采样算法确实提高了预测效果。在数据集Glass1和Yeast6上G-mean和AUC表现均高于其他方法，G-mean值最高提高了1.03%，AUC值提高了4.6%;对比经典的过采样算法SMOTE，G-mean值平均提高了约0.899%，AUC值平均提高了约4.44%;与ADASYN相比，本文提出過采样算法的评价指标均高于其指标;在Yeast3中本文算法的AUC均高于其他算法，而G-mean值略低的原因为RN降低程度高于RP增大程度。在Pima中本文算法的G-mean高于另外两种过采样算法，AUC值相对较低，分析其原因为Pima原始数据集中数据分布比较集中，对噪声样本的划分比较敏感，所以导致AUC的取值略低于其他两种方法。

3.5 本文分类模型与其他算法的比较

3.4节验证了本文采样算法的有效性，现进一步验证本文提出的基于改进的过采样方法与集成学习结合对分类模型的提升。本文算法与SMOTE-Boost、CUS-Boost和RUS-Boost在6个不同数据集上的G-mean、AUC比较结果，如表4所示（加粗部分为最好实验结果）。

从表4的实验结果可以看出，本文提出的分类模型在所选用的数据集上其G-mean值、AUC值上均得到了提升，在数据集Ecoli2、Glass1以及Pima中，其分类的效果均优于对比模型，G-mean值的最高值达到了88.2%，AUC的最高值达到了94.1%。在数据集Yeast3中本文算法的低于G-mean值、AUC值略低一些，原因为其数据集本身类别数据的分布区域较为重叠，多数类样本集中包含“干扰样本”。在数据集Yeast6中本文算法的G-mean值略低，但其AUC值最高提高了9.9%。对于数据集Glass6即使在G-mean值上低于SMOTE-Boost算法，但其AUC值增加了2.6%。

4 结语

针对不平衡数据集分类问题，现有的过采样算法更多地考虑类间数据的不平衡，进而忽略了类内样本的不平衡性，存在样本分布“边缘化”问题，导致合成样本的质量较低，实际情况下对样本的分类准确度较低。针对以上问题，本文在SMOTE算法的基础上进行改进。为了克服SMOTE算法的不足，本文在进行过采样之前，提出噪声样本过滤算法，对少数类样本集先进行噪声样本的滤除，提高合成样本的质量。其次针对合成样本存在的不平衡性问题，引入聚类思想，有效降低了数据集中类内的不平衡性，同时利用滤除噪声样本数、G-mean以及AUC进行模型参数的寻优。最后与AdaBoost算法相结合，在KEEL数据集上与其他方法进行对比，实验表明该分类模型可以明显提高少数类样本的分类准确度，分类性能更优。

本文将聚类思想引入到不平衡分类问题的过采样算法中，并与集成学习相结合提出一种针对不平衡数据二分类问题的KSMOTE-自适应增强（KSMOTE-AdaBoost）算法，并通过一系列实验验证了KSMOTE-AdaBoost算法训练出的分类器可以有效处理不平衡数据的分类问题。然而在实际应用中所接触的数据大部分是多类别的，未来将研究考虑针对多类的基于过采样的分类算法，提高分类的精度以及减少算法所运行的复杂度。通过，也期望本文所提出的不平衡数据集分类算法可以应用到更多的领域。

参考文献

[1]莫赞，盖彦蓉，樊冠龙.基于GAN-AdaBoost-DT不平衡分类算法的信用卡欺诈分类[J].计算机应用，2019，39（2）：618-622. （MO Z， GAI Y R， FAN G L. Credit card fraud classification based on GAN-AdaBoost-DT imbalanced classification algorithm[J]. Journal of Computer Applications， 2019， 39（2）： 618-622.）

[2]MAZUROWSKI M A， HABAS P A， ZURADA J M， et al. Training neural network classifiers for medical decision making： the effects of imbalanced datasets on classification performance [J]. Neural Networks， 2008， 21（2/3）： 427-436.

[3]YANG Z， TANG W， SHINTEMIROV A， et al. Association rule mining-based dissolved gas analysis for fault diagnosis of power transformers [J]. IEEE Transactions on Systems， Man， and Cybernetics， Part C （Applications and Reviews）， 2009， 39（6）： 597-610.

[4]PUN J， LAWRYSHYN Y. Improving credit card fraud detection using a meta-classification strategy [J]. International Journal of Computer Applications， 2012， 56（10）： 41-46.

[5]康松林，樊晓平，刘乐，等.ENN-ADASYN-SVM算法检测P2P僵尸网络的研究[J].小型微型计算机系统，2016，37（2）：216-220. （KANG S L， FAN X P， LIU L， et al. Research on P2P botnets detection based on the ENN-ADASYN-SVM classification algorithm[J]. Journal of Chinese Computer Systems， 2016， 37（2）：216-220.）

[6]BERMEJO P， GAMEZ J A， PUERTA J M. Improving the performance of Naive Bayes multinomial in e-mail foldering by introducing distribution-based balance of datasets [J]. Expert Systems with Applications， 2011， 38（3）：2072-2080.

[7]CHAWLA N V， BOWYER K W， HALL L O， et al. SMOTE： synthetic minority over-sampling technique [J]. Journal of Artificial Intelligence Research， 2002， 16（1）： 321-357.

[8]HE H， BAI Y， GARCIA E A， et al. ADASYN： adaptive synthetic sampling approach for imbalanced learning [C]// Proceedings of the 2008 IEEE International Joint Conference on Neural Networks （IEEE World Congress on Computational Intelligence）. Piscataway， NJ： IEEE， 2008： 1322-1328.

[9]HAN H， WANG W Y， MAO B H. Borderline-SMOTE： a new over-sampling method in imbalanced data sets learning [C]// Proceedings of the 2005 International Conference on Intelligent Computing， LNCS 3644. Berlin： Springer， 2005： 878-887.

[10]CASTRO C L， BRAGA A P. Novel cost-sensitive approach to improve the multilayer perceptron performance on imbalanced data[J]. IEEE Transactions on Neural Networks and Learning Systems， 2013， 24（6）： 888-899.

[11]李勇，劉占东，张海军.不平衡数据的集成分类算法综述[J].计算机应用研究，2014，31（5）：1287-1291.（LI Y， LIU Z D， ZHANG H J. Review on ensemble algorithms for imbalanced data classification [J]. Application Research of Computers， 2014，31（5）： 1287-1291.）