矩形积分双谱和半监督鉴别分析下的通信辐射源识别
韩国川, 张金艺,, 李 科, 何利康, 姜玉稀, 王 涛
(1.上海大学微电子研究与开发中心,上海200444;2.上海大学特种光纤与光接入网重点实验室,上海200444;3.上海三思电子工程有限公司,上海201100)
通信辐射源识别是通信对抗中电子情报/电子支援系统中的研究热点之一[1],是指将提取以电台为主的通信辐射源发射信号的细微特征作为指纹特征来进行分析,并利用先验信息确定该信号所属通信辐射源的类别,因此也称通信辐射源指纹识别.在军事通信对抗领域中,通信辐射源识别可以进一步查明对方的战术意图、威胁程度、指挥系统结构等信息,为己方有针对性地制定战略战术部署提供重大依据.
现有的通信辐射源识别方法大体上可划分为提取暂态信号特征和提取稳态信号特征这2种识别方法.提取暂态信号特征进行通信辐射源识别的方法主要通过与小波分析[2]、分形[3]等理论结合,对通信辐射源进行识别,但是实际应用中暂态信号具有瞬时性,信号数据较难被捕获.因此,当前主要以提取通信辐射源的稳态信号特征后进行识别作为研究热点.2014年,Lin等[4]采用信号分选技术,将载频、脉冲宽度、重复间隔这3个常规参数作为雷达辐射源的指纹特征来进行分选,随后利用改进的模糊神经网络分类器来识别雷达辐射源.该方法通过对分类器的改进来达到更好的识别效果,不过其选取的指纹特征对同类通信辐射源识别效果并不明显.针对指纹特征选取不精确从而不能有效处理同类通信辐射源的识别问题,2016年桂云川等[5]利用高阶谱分析技术,提取通信辐射源双谱特征作为其指纹特征,并利用支持向量机进行分类识别,得到分类结果.该方法一定程度上提升了同类通信辐射源识别效果,但是由于双谱特征维数较高,直接用于分类识别容易产生“维数灾难”问题,即同时在训练样本较少以及先验样本标签信息较少时其识别精度只有72%左右.为了解决直接应用双谱特征带来的“维数灾难”问题,2016年雷迎科等[6]针对通信辐射源双谱特征维数较高的问题,引入流形学习理论,提出正交局部样条判别流形嵌入算法来对通信辐射源双谱特征进行降维,再对降维后的双谱特征利用分类器进行识别.该方法降低了分类器规模并提升了识别精度,其平均识别率为82.37%.不过该算法属于无监督学习算法,即没有充分利用宝贵的样本标签信息来指导训练过程,未考虑在先验标签信息较少时识别精度不高的问题.
综上所述,本工作提出了一种基于矩形积分双谱和半监督鉴别分析的通信辐射源识别方法.当采集到通信辐射源发射的信号样本后,该方法采用矩形积分双谱算法提取通信辐射源双谱特征,并将其作为指纹特征,以表征所属通信辐射源;同时,采用结合流形学习和半监督学习的半监督鉴别分析算法,充分利用标记和无标记双谱特征样本,实现高维双谱特征维数的约简,并在低维子空间中进行分类识别,从而提升通信辐射源的识别效果.为了验证本方法的效果,采用同厂、同批、同型号的FM电台作为同类通信辐射源的代表进行电台识别实验.实验结果表明,在FM电台训练样本中具有先验标签信息的样本较少时,本方法对电台测试样本的识别率最高,为87.6%,充分证明了该方法在同类通信辐射源识别中,指纹特征提取和识别精度方面的优势.
1 通信辐射源双谱特征提取
通信辐射源“指纹特征”是指通信辐射源的细微特征,即使是同厂、同批、同型号的同类通信辐射源设备,由于受到环境、工艺等细小因素的影响,导致这些设备之间也存在微小差异,这些微小差异构成的细微特征即可作为通信辐射源的指纹特征来表征.通常,通信辐射源指纹特征大多表现为非平稳、非高斯、非线性,同时也需要满足时移不变性、尺度变化性、相位保持性这3种特性,而信号的双谱特征能够较好地满足通信辐射源指纹特征的特性,并且能够有效解决同类通信辐射源的指纹特征提取问题,因此本工作采用矩形积分双谱提取通信辐射源双谱特征作为其指纹特征,以表征所属通信辐射源.
1.1 通信辐射源识别流程
通信辐射源识别主要是通过通信接收机采集得到通信辐射源发射的原始信号数据,经过信号预处理后利用特征提取来提取出原始信号数据的指纹特征,以表征所属通信辐射源,并利用分类器对待识别原始信号数据所属通信辐射源进行分类识别,最终得出识别结果.通信辐射源的识别本质上可看作为模式识别问题,即通过对待识别对象进行特征提取后进行训练学习,最后进行分类判别的一个过程[7].一般来说,通信辐射源识别流程如图1所示.

图1通信辐射源识别流程Fig.1 Flow chart of communication emitter identification
图1 中特征提取的方法和精度,将直接影响到后续的计算复杂度以及分类识别的效果,因此选择合适的特征提取方法至关重要.
1.2 基于矩形积分双谱的通信辐射源双谱特征提取
传统的1阶、2阶或功率谱分析方法在用以进行通信辐射源发射信号特征提取时,普遍存在相位和幅度信息失真的问题,而信号的高阶谱能够克服这些问题,同时还能够有效抑制高斯噪声.在高阶谱中双谱阶数最低,但是双谱包含了高阶谱的所有特性,因此在通信辐射源识别中应用广泛[8].
双谱是3阶累积量的2维傅里叶变换.假设通信辐射源稳态信号为x(t),则其对应的3阶累积量可表示为
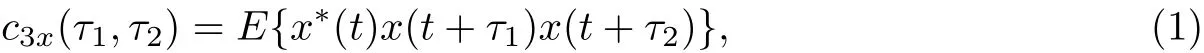
式中,x*为共轭,τ1和τ2为延迟.设X(w)为x(t)的傅里叶变换,则双谱B(w1,w2)为
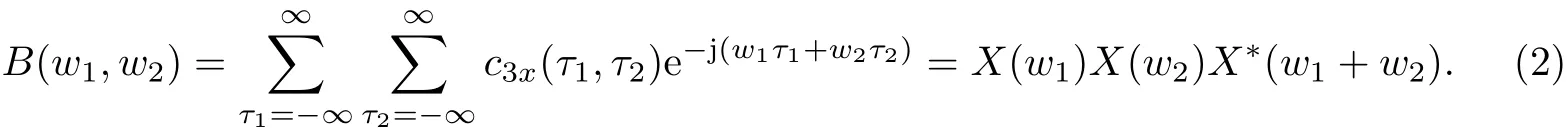
由于双谱的直接应用需计算2维匹配模板,因此为克服双谱直接应用产生的计算复杂问题,可设定积分路径,引入积分双谱的方法[9].积分双谱方法可分为径向积分双谱(radially integral bispectra,RIB)、轴向积分双谱(axially integral bispectra,AIB)、圆周积分双谱(circularly integral bispectra,CIB)和矩形积分双谱(square integral bispectra,SIB)这4种.积分双谱方法在信号双谱平面上设定不同积分路径,其积分路径如图2所示.
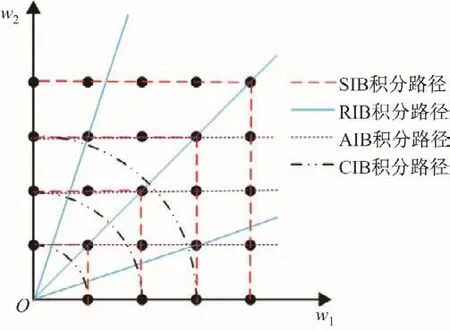
图2不同积分双谱的积分路径Fig.2 Integral path of different integral bispectrums
图2 中的黑点表示双谱值,w1和w2为频率坐标轴.从图中双谱平面上的积分路径来看,虽然RIB提取的双谱特征满足时移不变性,但是存在尺度信息和相位信息的丢失问题;AIB提取的双谱特征丢失了较多相位信息,不满足相位保持性;CIB提取的双谱特征也只保留了信号的部分相位信息;而SIB的积分路径是由一组以原点为中心的正方形组成,时移不变性、尺度变化性、相位保持性都能满足.同时,从图2也可看出,RIB,AIB,CIB在提取双谱特征过程中都有遗漏或复用双谱值的问题,会影响后续分类识别的准确性,而SIB则不存在这个问题.4种积分双谱方法提取的双谱特征特性如表1所示.

表1 4种积分双谱方法提取的双谱特征特性Table 1 Bispectra features of four integral bispectra methods
SIB提取的双谱特征能够满足表1中的3种特性,也没有出现对信号双谱值的遗漏或复用,从而能够获取通信辐射源的重要信息特征;同时SIB对噪声也存在仍较强的抑制作用.因此,采用SIB提取的双谱特征作为指纹特征来表征所属通信辐射源是十分合适的.
利用SIB提取通信辐射源双谱特征的算法步骤如下.
(1)假定有待识别的通信辐射源分属c类,每类通信辐射源采集N个样本信号,其中第i类通信辐射源的第k个样本信号可表示为xik(n).
(2)通过式(2)计算样本信号xlk(n)的双谱Bik(w1,w2),根据图2中SIB的积分路径来计算SIB提取的双谱特征即
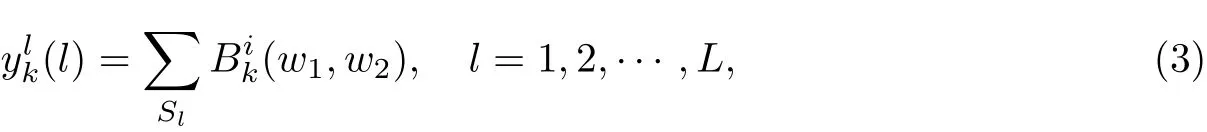
式中,L为SIB的积分路径总条数,Sl为图2中SIB采用的第l条积分路径.
信号双谱特征向量维数与SIB采用的积分路径条数L相同,为了保留相对较多的的信号双谱特征,需要选择相对较多的积分路径条数,导致信号双谱特征向量维数也相对较高.随着维数的增加,双谱特征向量中冗余信息也会增多,致使不同的双谱特征向量在高维特征空间中无序分布并产生交叠.同时,特征维数的增加也会导致所需的信号样本呈指数级增加,因此如果直接采用高维双谱特征作分类识别也将会出现“维数灾难”问题,导致一些分类器(如KNN,SVM)时效性降低,识别率下降.因此为了提高识别率,必须对高维双谱特征向量进行降维处理.
2 通信辐射源双谱特征降维与识别
由于传统的降维技术大多是线性降维方法,不能有效针对具有大量非线性结构的通信辐射源双谱特征数据进行降维,同时在实际应用中存在较难获取标签通信辐射源信号的情况,导致先验信息较少,从而产生识别精度不高的问题.因此,在通信辐射源识别中,可以引入结合流形学习[10-11]和半监督学习的半监督流形学习方法[12-13].半监督鉴别分析(semi-supervised discriminant analysis,SDA)算法是一类基于图嵌入的半监督流形学习算法[14-15],本工作将SDA算法引入到通信辐射源识别中,根据双谱特征数据本身的非线性流形信息和部分标签信息,将高维双谱特征数据映射到低维子空间后进行分类识别,从而提升通信辐射源识别性能.
2.1 半监督鉴别分析算法原理
式中:a为高维数据在其低维子流形上的投影向量;Sb和St分别为类间散布矩阵和整体散布矩阵,
系数β用来平衡模型复杂度和损失惩罚度;J(a)为流形正则化项,用来约束目标函数,
当存在无标签样本数据时,可以构建一个具有流形结构的流形正则化项J(a),用来约束目标函数.数据一致性的先验假设是SDA算法的关键,即对于分类问题,如果数据点相互邻近,则其都具有相同的标签.那么,对于样本集的一致性关系矩阵Sij的定义为
式中:Sij表示为数据点之间对应的权重矩阵;Np(xi)为样本数据点xi的p最近邻集合,p通常采用经验值.令X=[x1,x2,···,xm],那么流形正则化项J(a)可表示为
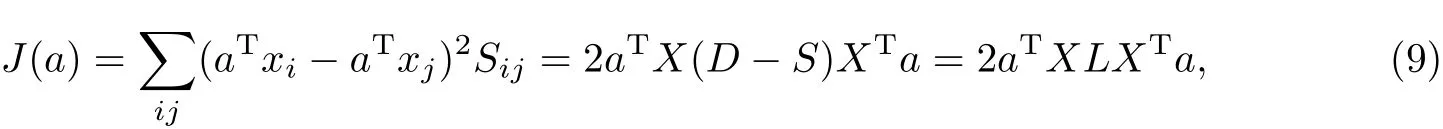
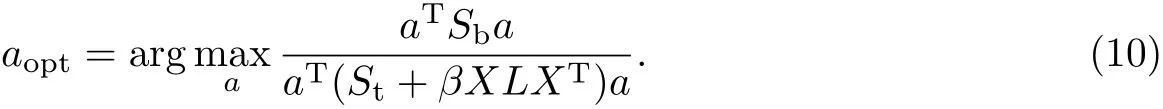
利用拉格朗日乘数法对式(7)进行求解,将其转换为特征向量求解的过程,即

式(8)中λ为该式的特征值,a为λ对应的特征向量.通过式(9)求得的对应c个非0特征值的投影向量集合A=[a1,a2,···,ac]即为投影转换矩阵,通过集合A即可将高维样本数据映射到其对应的低维子空间中,

2.2 半监督鉴别分析下的双谱特征降维与分类识别
将SDA算法应用在通信辐射源高维双谱特征降维和识别中,其具体流程如下.
(1)假定有待识别的通信辐射源分属c类,共含有m个双谱特征数据矩阵为双谱特征向量的原始维度),其中含有具有c个辐射源个体类别的l个有标签双谱特征样本集和m-l个无标签双谱特征样本集为双谱特征样本xi的类别标签,lk为第k类有标签双谱特征样本的数量,且为第k类双谱特征样本的均值向量,μ为全部双谱特征样本的均值向量.
(2)利用式(5)和(6)计算出双谱特征数据的类间散布矩阵Sb和总体散布矩阵St.
(3)构建p-近邻图,通过式(10)求得一致性关系矩阵Sij,并计算拉普拉斯矩阵L.
(4)求解式(11)的特征方程式,得到c个投影向量:a1,a2,···,ac.
(5)令A=[a1,a2,···,ac],通过式(12)将通信辐射源原始高维双谱特征数据矩阵X映射到c维子空间,得到降维后的双谱特征数据矩阵Z.
(6)对降维后的双谱特征数据进行分类识别,得到通信辐射源识别结果.
利用SDA算法对通信辐射源双谱特征数据进行降维与识别,其流程如图3所示.
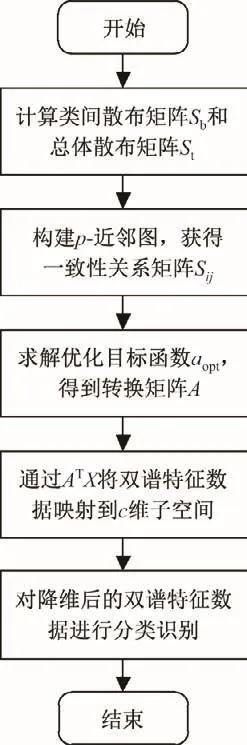
图3 通信辐射源双谱特征样本应用SDA算法流程Fig.3 Flow chart of SDA algorithm on bispectra characteristic samples
SDA算法在降维过程中能有效利用有标签和无标签双谱特征样本来提高鉴别能力.有标签双谱特征样本用来最大化不同通信辐射源双谱特征数据的类间分离性,无标签双谱特征样本用来估计出双谱特征数据的内在流形结构,挖掘出维数低、复杂度低的双谱特征,这不仅简化了计算复杂度,同时避免了数据和资源的浪费,提高了通信辐射源识别精度.
3 验证体系构建与结果分析
在构建验证系统时,为验证矩形积分双谱和半监督鉴别分析下的通信辐射源识别方法效果,采用同类的10部FM电台代表同类通信辐射源,以及一台计算机进行电台识别实验,并通过2组实验来说明本算法的有效性.
3.1 验证体系构建
本工作所采用的10部FM电台,信道带宽为25 kHz,中心频率为410 MHz.接收FM电台发射信号的接收机信道带宽为100 kHz,采样频率为204.8 kHz,采样点数为1 023 658个点.采样处理后得到的数据为零中频I/Q正交数据.每部电台分别采样9段样本信号.本工作使用Matlab R2012a软件进行仿真实验,不同于一般仿真实验,本工作用于仿真实验的电台数据是从真实场景中接收得到;用于仿真的计算机型号为联想Y470P-IFI,CPU主频和型号分别为2.5 GHz和i5-2450M双核处理器,内存为8 GB.
对于每部FM电台,通过射频接收机对FM电台的发射信号进行接收和预处理,获得I/Q2路数字零中频信号,并将该时域信号作为后续处理的样本信号数据.计算机接着将样本信号数据分为训练样本和测试样本,最终识别出测试样本信号数据所属FM电台.FM电台训练样本采用如式(13)所示的通过矩形积分双谱提取出电台的双谱特征,随后利用式(14)通过半监督鉴别分析算法计算出投影转换矩阵.测试样本用于测试识别的结果,测试样本同样根据式(15)提取出双谱特征后,使用训练样本求出的投影转换矩阵,将高维双谱特征数据映射到低维子空间,然后进行分类识别,得出最终FM电台的识别结果.整个电台识别系统流程如图4所示.
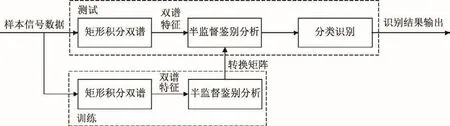
图4 电台识别系统流程Fig.4 Flow chart of radio identification system
3.2 实验结果分析
本工作进行2组实验来说明本算法的效果,其中一组为分析双谱特征表征所属通信辐射源效果实验,另一组为评价矩形积分双谱和半监督鉴别分析下的通信辐射源识别方法的性能实验.
第一组实验从10部FM电台中任选3部电台的样本信号,分别提取其双谱特征,通过双谱的截面图及双谱立体图进行显示对比,双谱截面图即为通过沿双谱立体图按平面f1=f2得到的截面.10部FM电台中的3部电台样本信号的双谱截面图及立体图如图5所示.
从图5中可以看出,不同电台的双谱特征是存在着细微差异的,同时将1.2节中提到的双谱作为阶数最低的高阶谱,计算复杂度相对较低且不存在相位和幅度的失真问题,以及抑制噪声的优势.因此,双谱特征可作为通信辐射源信号指纹特征来表征所属通信辐射源.
第二组实验根据图4的电台识别系统设计流程,从10部FM电台中的每部电台采样样本随机选择m(m=3,4,5,6,7)个样本作为训练集,共有10m个训练样本;将每部电台的其余9-m个采样样本作为测试集,测试样本总数为10×(9-m);随后每部电台训练集中随机选取2个样本标记所属电台标签,剩余m-2个训练样本标签未知.对于本工作采用的SIB算法,在利用式(16)提取电台双谱特征时,为了保留相对较多的信号双谱特征以保证识别精度,假设傅里叶变换点数为512点,即釆用256条积分路径计算得到对应的双谱特征向量的维数为256维.对于SDA算法,在求解式(8)一致性关系矩阵Sij时,构建p-近邻图的邻域个数设为3,式(4)中参数β设为0.1,那么利用式(17)通过半监督鉴别分析算法计算出投影转换矩阵后,根据式(12)将高维双谱特征数据映射到低维子空间,即得到降维后的电台双谱特征向量维数为10维.为了验证本算法,分别采用矩形积分双谱(SIB)、矩形积分双谱+半监督鉴别分析(SIB+SDA)、矩形积分双谱+主成分分析(SIB+PCA)3种不同方法对FM电台进行特征提取并识别,分类器统一选用最近邻分类器(1-nearest neighborhood,1-NN).为了避免单次识别实验结果的随机性,将每种方法20次实验得到的平均识别率作为测试结果.3种算法识别FM电台的结果如表2和图6所示.
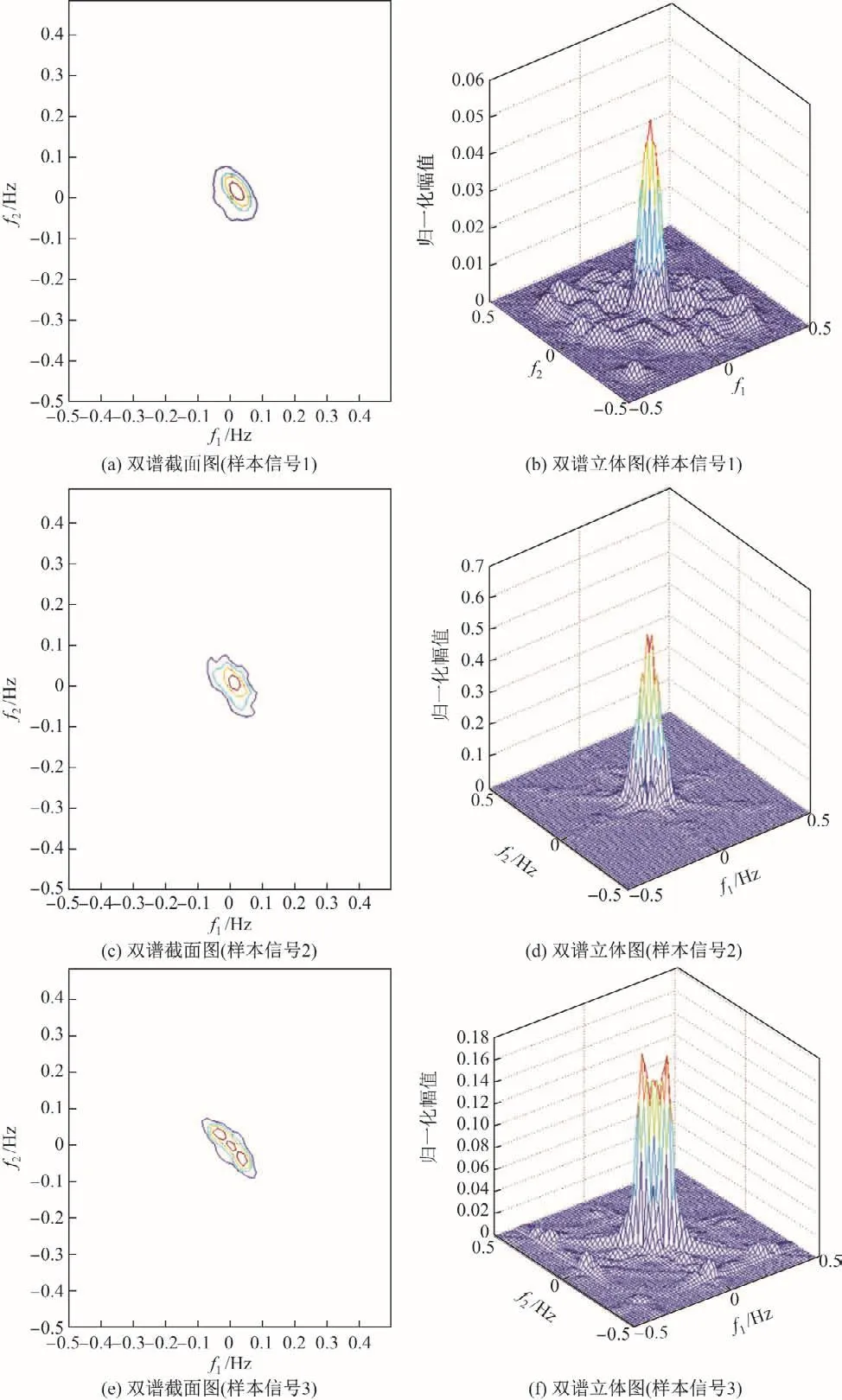
图5 3部电台样本信号的双谱截面图及双谱立体图Fig.5 Bispectra sectional view and stereogram of 3 radio sample signals
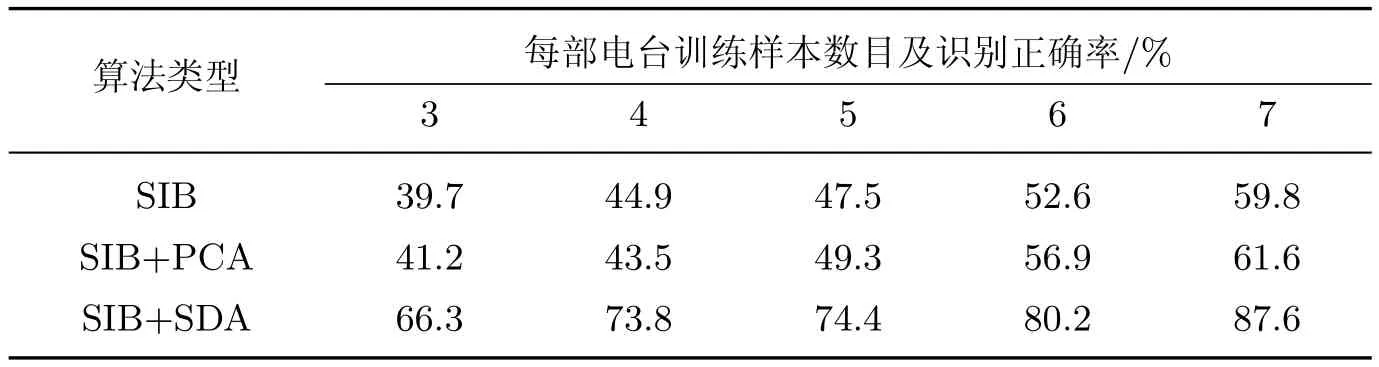
表2 3种算法识别FM电台结果比较Table 2 Comparisons of different algorithms to identify FM radios
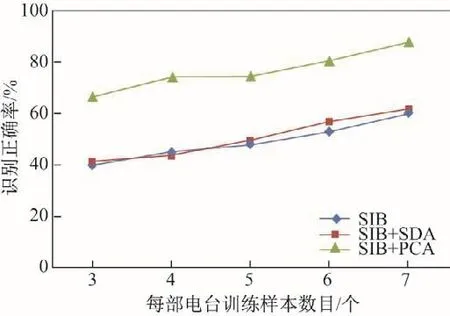
图6 3种算法识别FM电台结果折线图Fig.6 Line chart of different algorithms to identify FM radios
表2和图6显示了在训练集中有标签电台样本数目较少的情况下,3种算法的电台识别结果.实验结果表明,本工作提出的SIB+SDA算法的识别效果较其他2种算法更佳.只使用SIB算法,即不处理双谱特征向量,直接进行后续分类识别,计算复杂度高且会造成不同的FM电台信号双谱特征在特征空间中产生交叠,导致电台识别率较低.而SIB+PCA算法虽然对双谱特征向量有降维效果,但是由于PCA属于全局线性降维方法,很难有效处理FM电台双谱特征这种具有大量非线性结构的数据,故导致识别率也不是很高.同时,在有标签样本较少,即训练样本中有标签电台样本数目只有2个时,随着训练样本数目的增加,本工作提出的SIB+SDA算法识别率相比于其余2种算法有显著提升,这是由于本算法通过SIB提取出电台双谱特征后,利用SDA算法对双谱特征进行降维,并根据有标签电台双谱特征数据来最大化不同电台样本数据的类间分离性,无标签电台双谱特征数据则用来估计电台样本数据的内在流形结构,从而提高了识别精度,其对测试电台样本的识别率最高达87.6%;而SIB和SIB+PCA算法并没有发挥无标签样本的作用,即使训练样本再加入无标签样本,识别率提升效果也不好,其最高识别率分别为59.8%和61.6%,相比较后有效地显示出SIB+SDA算法在有标签电台样本较少时的电台识别性能.
4 结束语
针对传统同类通信辐射源识别方法中存在的指纹特征难以提取,以及在先验标签信息较少时识别精确度不高的问题,本工作以指纹特征差异微小的同类通信辐射源为对象,提出了一种基于矩形积分双谱和半监督鉴别分析的通信辐射源识别方法.该方法采用矩形积分双谱算法提取通信辐射源双谱特征,将其作为指纹特征,以表征所属通信辐射源;同时,采用半监督鉴别分析算法,根据双谱特征数据的部分标签信息和非线性流形信息,将高维双谱特征数据映射到低维子空间后进行分类识别,从而提升通信辐射源识别性能.在同类FM电台上的识别实验表明,在FM电台训练样本中具有先验标签信息的样本较少时,本工作所提方法对电台测试样本的识别率最高达87.6%,仍然具有较高的识别精度.矩形积分双谱和半监督流形学习下的通信辐射源识别方法,具有在同类通信辐射源识别中指纹特征提取和识别精度方面的优势,因此可广泛应用于电子信息对抗、频谱管理等领域,具有非常高的军事和社会应用价值.

