深水钻井隔水导管承载能力影响因素分析
刘清友, 秦 松, 毛良杰, 王国荣
(1. 油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都 610500;2. 西南石油大学能源装备研究院,四川成都610500)
深水钻井中,水下井口及隔水导管受到的载荷非常复杂。轴向外载荷主要来自装备自身的重力和挠性接头传递的轴向载荷,井口还受到来自防喷器组顶部挠性接头传递的横向与轴向载荷[1-2]。此外,海流也会对井口产生横向载荷。深水钻井中,由于海底井口失稳造成隔水导管变形而导致的安全问题时有发生,而且结果往往较为严重,有时甚至会使整口井报废。因此,分析深水钻井中隔水导管的承载能力具有现实意义。
目前,深水钻井隔水导管力学分析已成国内外研究的重点,但研究主要集中在隔水管的变形、等效应力随管身分布情况和剩余寿命等方面,关于井口以深隔水导管承载能力方面的研究则较少[3-5]。虽然有人研究指出深水钻井隔水导管可能存在失稳甚至报废风险,但并没有建立相应的理论体系。例如,G. W. King[6]采用有限元方法对深水钻井中隔水导管的稳定性及井口疲劳失稳问题进行了研究,但没有建立起相应的理论;R. Juiniti 等人[7]总结了Campos 盆地深水钻井作业中有关海底井口力学稳定性的经验教训,探讨了不同水深条件下不同尺寸隔水导管的稳定性,但未形成理论体系;Guan Zhichuan 等人[8]采用有限差分法对浅部隔水管柱以及海底井口的侧向偏移进行了静力学数值求解,求解时考虑了管柱轴向力的影响,但未涉及井口以深隔水导管的稳定性问题;苏堪华等人[9]利用土力学桩基理论中的地基反力 p-y曲线研究了深水钻井井口的稳定性,但对受力进行简化后忽略了横向载荷,且认为海底土壤性质恒定不变,与实际情况有较大出入;张伟国等人[10]利用有限元方法计算分析了隔水导管出泥高度对井口稳定性的影响,但建立的模型较为粗略,考虑的影响因素较少,计算结果精度不高;周正波[11]研究了钻井液稳定循环和力学稳定条件下的井口稳定性,但模型建立在特定地层基础之上,不具有普适性。为了解决井口以深隔水导管的稳定性问题,深入分析深水钻井隔水导管承载能力的影响因素及影响规律,笔者采用力学等价转化计算方法,将深水井口上部的防喷器组及隔水管下部挠性接头对井口的作用力进行传递简化,然后考虑隔水导管受到横向与轴向载荷的作用,采用ANSYS 建立管-土应力作用和变形过程的模型,并通过算例分析了井口作用力、隔水导管外径和壁厚、井口出泥高度及地基类型对隔水导管承载能力的影响,以期为现场施工及相关理论研究提供指导。
1 井口受力分析
深水钻井作业系统的主要组成如图1 所示,其中,隔水管是重要部件,除了承受井口防喷器的重力以外,还直接承受下入井中的钻柱的浮重;同时,随着隔水管长度增大,由海流产生的横向作用力也随之增大;而且,其通过隔水管底的挠性接头传递加到海底井口及下部导管上,对井口及隔水导管产生不可忽视的轴向及横向作用力[12-13]。对于一些特定海域,如南海海域,海底土通常为淤泥和沉积物,塑性较高,密度较低,含水量和孔隙度比通常情况下要高,故其对隔水导管的地基反力相比陆地更不稳定[14]。
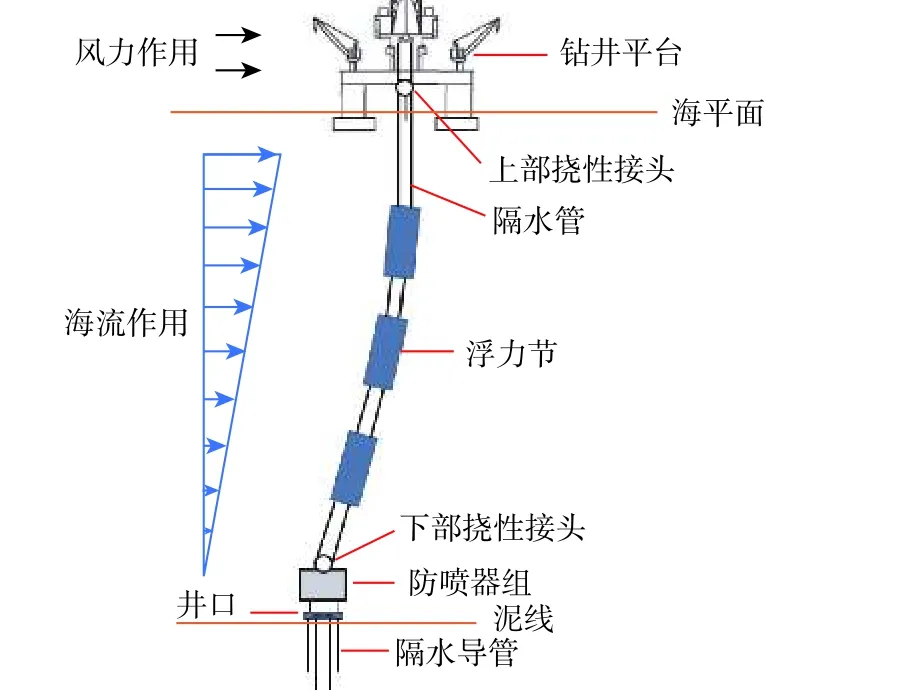
图 1 深水钻井作业系统示意Fig. 1 Schematic diagram of deepwater drilling system
对井口以上的装置对井口施加的外载荷向井口进行等效转化,就可以在不同工况下采用相同模型进行隔水导管承载能力分析,其简化情况如图2所示(图2 中: fr, fb和 fw分别为海流施加给隔水管、重型防喷器组和井口的横向载荷,kN; ff, Ff分别为通过隔水管底的挠性接头传递给井口的横向载荷和轴向载荷,kN; Fr, Fb和 Fw分别为隔水管、重型防喷器组和井口的浮重,kN)。对井口的受力情况进行简化,从而为建模提供基础。
根据作用力与反作用力的原理进行简化[15],其力学等效转化公式为:

式中:F1为井口承受的等效横向载荷,kN;F2为井口承受的等效轴向载荷,kN。
2 隔水导管承载能力分析模型
为了使模型计算时更易于收敛,建立模型前首先进行合理假设:1)由于隔水导管长度与其横截面积相差极大,所以忽略其底端与土壤接触产生的承载力,近似认为支撑力主要来源于管侧与土壤的静摩擦力;2)隔水导管为各向同性、均质、线弹性钢制管柱,且管段接头的局部影响可以忽略不计;3)隔水导管在重力和外部作用力的共同作用下只发生微小变形。
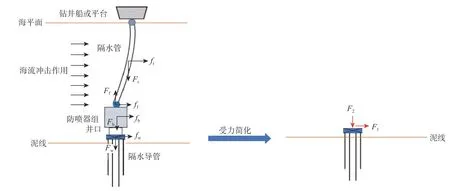
图 2 深水钻井中井口受力简化示意Fig.2 Simplified schematic of wellhead force conditions in deepwater drilling
根据式(1)和式(2),结合以上假设条件,在ANSYS 中建立三维有限元模型,分析隔水导管耦合受力情况下的力学响应情况。由于模型是对称的,因此使用对半模型进行分析。隔水导管采用单元库中适合模拟线性、弯曲及适当厚度的Shell 43 单元进行模拟;根据海底地层的性质,土壤采用Drucker-Prager 模型进行模拟。
分别建立土壤模型和隔水导管模型。建立土壤模型时,设置扰动半径为50 倍管径,影响深度为30.00 m。分别对管与土壤设定相应的约束条件:模型底部限制3 个方向(x 轴、y 轴和z 轴方向)的位移,土壤周边分别限制其在x 轴和y 轴上的位移,模型的对称面限制其在y 方向上的位移。设定2 个接触对,即导管侧-井壁接触和导管端-井底面接触。施加横向与轴向载荷时,其受力端面均为导管上部截面。
对土壤模型划分网格时,重点加大井筒附近海底土的网格数量,划分结果如图3 所示。隔水导管共划分328 个网格,海底土共划分15 224 个网格。

图 3 深水钻井井口三维有限元模型示意Fig. 3 3D finite element model of a deepwater drilling wellhead
3 算例及影响因素分析
3.1 隔水导管及地层参数设置
基于上文建立的模型,以南海某区块为例进行实例计算。隔水导管的弹性模量取210 GPa,泊松比取0.3[11]。结合该区块具体的地质参数,在ANSYS中将土壤分成7 层进行有限元建模,各层的土质参数见表1。其中,顶部2 层海底土弹性模量取2 MPa,3—7 层弹性模量取10 MPa,泊松比取0.4。
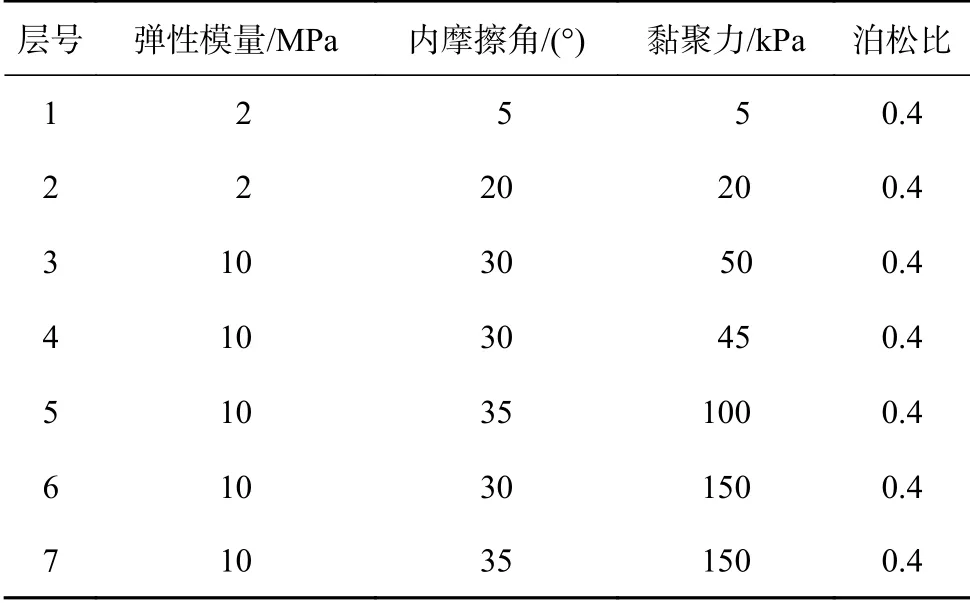
表 1 南海某区块各层的土质参数Table 1 Soil parameters of each formation in a block in the South China Sea
3.2 井口载荷计算
目前,隔水导管大多采用喷射方法下入。隔水导管下入之后,在轴向上承受一系列复杂的载荷,这些载荷在不同工况下会有较大变化。如果导管柱的轴向承载能力不够,管柱就会下陷甚至失稳,最终导致整口井报废。其中,最危险的工况(轴向载荷最高)发生在安装隔水管和防喷器组之前,如图4 所示(图4中: Fc为某时刻隔水导管的管侧阻力,kN; Fd为某时刻隔水导管的管端阻力,kN)。表层套管悬挂在井口上,所有轴向作用力均由隔水导管承载[16-17]。
隔水导管的初始承载能力计算公式为:

图 4 最危险工况时的隔水导管受力示意Fig. 4 Schematic of conductor stress states under the most risky conditions
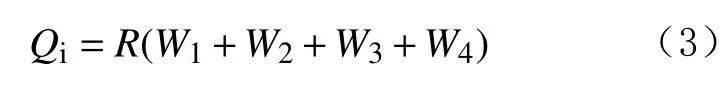
其中

当阻力与初始承载能力达到平衡时,有:

式中: Qi为初始承载能力,kN;R 为钻压利用率,一般为0.8~1.0; W1为 隔水导管浮重,kN; W2为低压井口头在海水中的浮重,kN; W3为喷射钻具在海水中的浮重,kN; W4为 导管送入工具的浮重,kN; ω1为38.0 mm厚钢材单位长度的浮重,kN/m; ω2为25.0 mm 厚钢材单位长度的浮重,kN/m; L1为38.0 mm 厚钢材的长度,m; L为隔水导管的设计下深,m; ωc为喷射钻具单位长度的浮重,kN/m。
表2 和表3 分别为南海某区块3 口井的钻井施工参数与套管下入层序,结合式(3)—式(6),计算出3 口井井口所受轴向载荷情况(见表4)。

表 2 南海某区块钻井施工参数Table 2 Drilling parameters of a block in the South China Sea

表 3 南海某区块套管下入层序Table 3 Casing program of a block in the South China Sea
根据该区块当前的风浪流作用特点,设水下井口在海洋环境极端恶劣情况下的最大横向压力为1.2 MPa[15]。通过上述计算分析,分别得到了水下井口所承受的横向及轴向载荷,并以此作为后续分析中设置参数的基准数据,进而开展影响因素分析。
3.3 影响因素分析
3.3.1 井口所受载荷
利用已经建立的三维有限元模型,结合该区块中井口的受力特点,对隔水导管顶部截面施加剪切形式的横向压力与法向压力,模拟参数见表5,井口所受作用力对隔水导管横向位移与Mises 应力的影响如图5 所示。
对A1、A2 和A3 组进行对比,发现:1)保持轴向压力不变,增大横向压力,隔水导管上部的横向位移逐渐增大,如图5(a)所示;2)横向压力除了引起隔水导管横向位移的变化,还会影响隔水导管的Mises 应力,如图5(b)所示。随着横向压力增大,Mises 应力峰值明显增加,表明井口受到的横向压力对Mises 应力峰值有显著影响;同时,对比3 条曲线发现,井口横向压力的变化对隔水导管横向位移及Mises 应力分布的影响比较小,两者均在增大到峰值后迅速单调减小,不同横向压力下的横向位移及Mises 应力收敛的位置均相同,Mises应力峰值也出现在同一深度(10 m 左右)。

表 4 南海某区块井口轴向载荷计算Table 4 Calculation on the wellhead axial loads of a block in the South China Sea

表 5 表面牵引力与法向压力设置Table 5 The setting of surface traction and normal pressure
对A3、A4 和A5 组进行对比,发现:1)在横向压力相同的情况下,轴向压力的变化对隔水导管横向位移影响甚微,如图5(c)所示;2)同时,在横向压力相同的情况下,随着轴向压力增大,隔水导管的Mises 应力出现了显著变化,相同深度的Mises 应力都显著增大,应力峰值也显著升高,如图5(d)所示。但值得注意的是,Mises 应力沿管身的分布趋势基本相同,峰值深度以及收敛深度均相同。

图 5 井口所受载荷对隔水导管横向位移与Mises 应力的影响Fig.5 Effect of wellhead force on Mises stress and lateral displacement of riser
对比分析图5(a)、图5(b)、图5(c)和图5(d)发现,管身横向位移和Mises 应力在一定深度下基本保持不变,井口所受横向压力与轴向压力的作用效果主要集中在隔水导管的上部区域,对隔水导管下部影响甚微。因此,实际施工时要重点关注隔水导管上部的受力情况,采取适当方法增大上部导管强度,避免其因受力过大而失效,从而保证钻井作业安全。
增添了A6 和A7 作为对照组,作进一步分析。A6 组只作用最大表面牵引力,A7 组只作用最大法向压力,结果见图5(e)和图5(f)。由图5(e)可知,只有法向压力作用时,横向位移无变化,始终保持为零;只有横向压力作用时,横向位移分布与耦合时基本一致,说明法向压力对横向位移的影响甚微。由图5(f)可知,只有法向压力作用时,Mises 应力分布虽然与耦合时一致,但其数值大大减小,峰值应力仅为耦合情况下的22%,隔水导管下部平均应力仅为3 MPa 左右;只有横向压力作用时,Mises 应力变化幅度很小,仅为峰值应力的3%,以上分析结果均不符合实际情况。

图 6 隔水导管外径和壁厚对横向位移与Mises 应力的影响Fig.6 The effect of conductor outer diameter and wall thickness on the Mises stress and lateral displacement of conductor body
综上可知,采用耦合模型进行分析能够得到较为明显的隔水导管横向位移及Mises 应力变化,贴近现场施工实际情况,对现场施工更具指导作用。
3.3.2 隔水导管直径与壁厚
以隔水导管的外径和壁厚作为研究对象,分析其对井口稳定性的影响,数据设置见表6,隔水导管外径和壁厚对横向位移与Mises 应力的影响如图6 所示。

表 6 隔水导管外径和壁厚Table 6 The outer diameter and wall thickness of conductor
由图6(a)可知:隔水导管壁厚保持不变,隔水导管外径增大,隔水导管横向位移逐渐减小;隔水导管外径保持不变,隔水导管壁厚增大,隔水导管的横向位移逐渐减小,说明其抗弯能力逐渐增强。由图6(b)可知:井口横向载荷和轴向载荷保持在一定范围的情况下,隔水导管外径和壁厚的变化对沿管身的Mises 应力分布趋势影响较小;壁厚变化时,Mises 应力峰值变化更加显著,说明与隔水导管外径相比,壁厚对Mises 应力峰值的影响更加明显。因此,实际施工时可以适当增大隔水导管靠近井口部位的外径和壁厚,从而增强隔水导管的承载能力,提高井口的稳定性。
3.3.3 井口出泥高度和地基类型
以井口的出泥高度和海底地基类型为研究对象,分析其对井口稳定性的影响,基本参数设置见表7,井口出泥高度和地基类型对隔水导管横向位移与Mises 应力的影响如图7 所示。
由图7 可知:保持地基类型一致,井口距泥线的高度增大,隔水导管上部的横向位移和Mises 应力也相应增加,表明海底水流对井口的冲击会显著影响水下井口的稳定性;地基类型为黏性土时的隔水导管上部横向位移和Mises 应力均比地基类型为砂性土时要大;隔水导管在黏土中受到井口载荷影响的长度要比在砂性土中大。因此,深水钻井时要结合该区块的地质特点设置合理的井口出泥高度,力求做到经济合理,兼顾成本与安全。

表 7 井口出泥高度和地基类型Table 7 The wellhead above-mudline height and foundation type
3.3.4 入泥深度
以隔水导管的入泥深度为研究对象,分别设置隔水导管入泥深度为20.00,30.00,40.00,50.00,60.00 和70.00 m,分析其对井口稳定性的影响,结果如图8 所示。

图 7 井口出泥高度和地基类型对隔水导管横向位移与Mises 应力的影响Fig.7 Effects of wellhead above-mudline height and foundation type on the Mises stress and lateral displacement of conductor

图 8 隔水导管入泥深度对横向位移与Mises 应力的影响Fig.8 Effect of the driving depth of conductor on the Mises stress and lateral displacement of conductor bodies
由图8(a)可知:随着隔水导管下入深度增大,井口处的横向位移逐渐减小;入泥深度为40.00~70.00 m 时井口处横向位移的增幅很小;但入泥深度由40.00 m 减至30.00 m 时井口处的横向位移突然增大。由此推测,在此地质条件下隔水导管最小入泥深度应为30.00~40.00 m。由图8(b)可知:隔水导管入泥深度为20.00~40.00 m 时,随着入泥深度增加,Mises 应力并不会收敛于一个定值,而是一直减小至管底;入泥深度增大到50.00 m 时,Mises 应力就会向同一深度处收敛。
有限元分析结果表明,隔水导管的入泥深度对其在井口处的横向位移与Mises 应力影响明显,若下入深度过小,会造成在极限工况下横向位移过大,导致井口失稳;若下入深度过大,又会造成施工成本升高。因此,深海钻井时需要确定经济合理的隔水导管入泥深度。
4 结 论
1)井口横向载荷是影响隔水导管横向位移的主控因素,而轴向载荷对隔水导管的横向位移作用并不显著;随着入泥深度增加,隔水导管横向位移逐渐减小,而Mises 应力则先增大后减小,其中位移和应力在隔水导管入泥深度10.00 m 左右存在拐点,故可以在一定深度以浅加大管柱的外径及管壁厚度,以提高隔水导管在耦合作用力下的稳定性;不同地基力学性能对隔水导管位移及应力分布的影响极其明显,隔水导管在砂性地基中的承载能力较黏性地基中要高。
2)隔水导管入泥深度存在临界值,当入泥深度小于临界值时,横向位移和Mises 应力变化都会对隔水导管承载能力造成恶劣影响,故可采用此模型进一步研究确定经济合理的下入深度,为现场施工提供指导。
3)深水钻井中,井口受到上部加大加重防喷器组的重力、隔水管底部挠性接头传递载荷、海流以及钻井船或钻井平台的共同作用,故合理设置隔水导管顶部的张紧力和钻井平台或钻井船的漂移数值,可以进一步提高深水钻井中隔水导管的稳定性。

