初中数学解题课教学策略课例分析*——以“勾股定理中的翻折问题”解题教学为例

广东省广州市华侨外国语学校(510095)陈锦喜

广东省广州市越秀区教育发展中心(510080)吴平生

数学离不开解题,波利亚曾指出：“掌握数学意味着善于解题”.下面以“勾股定理中的翻折问题”解题教学为例,通过创设问题情境、暴露思维过程、突破解题难点、提炼解题方法,引导学生发现问题与提出问题,让学生经历“从无到有”的探究过程、“由误到悟”的试误过程、“由表及里”的提炼过程,实现从“一题多解”到“多解归一”,从“一题多问”到“一题多变”的转变,达到“解一题、会一类、通一片”的教学效果.

一、创设问题情境,学会提出问题

解题教学需要创设合适的问题情境,选择有一定挑战性的问题,可以激发学生的探究欲望,提升学生的数学思维.在“勾股定理中的翻折问题”引入中,笔者创设了如下两个问题情境.

问题1如图1,在Rt△ABC中,∠A=90°,AB=8,AC=6,将△ABC沿DE翻折,使点B与点C重合.

（1）你能直接求出图1中哪些线段的长？（2）你还能求出图1中其它的线段长吗？

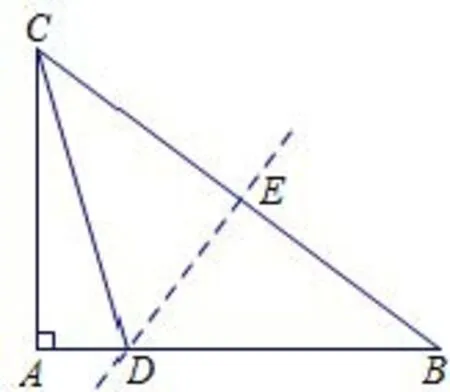
图1

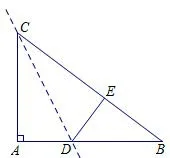
图2

问题2如图2,在Rt△ABC中,∠A=90°,AB=8,AC=6,将△ABC沿CD翻折,使点A与BC边上的点E重合.

（1）问题2 与问题1 有哪些相同与不同之处？

（2）你能类比问题1 提出问题并加以解决吗？

问题1 具有一定的启发性与开放性,有助于学生从“已知→可知→未知”的自然过渡.问题2 与问题1 具有一定的相似性与类比性,有助于学生在模仿与比较中学会类比与迁移,培养学生发现问题和提出问题的能力.

二、暴露思维过程,学会分析问题

解题教学是解题活动的教学,是师生再发现与再创造的过程.解题教学不仅要解决具体问题,而且要从解决具体问题的过程中学会怎样解题,这就需要暴露解题思维过程.下面以问题1 与问题2 的师生对话为例来展现解题思维过程.师：问题1 是一个什么问题？

生（齐）：翻折问题.

师：看到翻折你会想到什么？

生（齐）：全等.

师：全等有什么性质？

生（齐）：对应边相等,对应角相等.

师：在图1中,你能得到哪些相等的边与哪些相等的角？

生（齐）：BD=CD,BE=CE;∠BDE=∠CDE,∠DBE=∠DCE,∠BED=∠CED=90°.

师：在图1中,你能直接求出哪些线段的长？

生1：因为∠A=90°,AB=8,AC=6,所以BC=10.因为△BDE～=△CDE,所以BE=CE=5.

师：在计算过程中,你用到了哪些知识与方法？

生1：用到了勾股定理,用到了三角形全等,用到了直接法.

师：你还能求出图1中剩余的线段长吗？

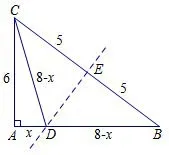
图1.1

生2：我是这样想的.如果能求出AD的长,那么就可以求出BD和CD的长,进而利用勾股定理可以求出DE的长.设AD=x,则CD=BD=8-x.在Rt△ACD中,x2+62=(8-x)2,解得所以

师：在计算过程中,你用到了哪些知识与方法？

生2：用到了勾股定理,用到了三角形全等,用到了间接法和方程思想.师：下面我们来回顾一下解题过程：“标已知→标可知→找关系→找Rt△→设未知→列方程→解方程”,如果分别选取一个动词来概括上述过程,可以怎样概括？

生3：“标→找→设→列→解”.

师：很好.下面我们来看问题2,问题2 与问题1 有哪些相同与不同之处？

生4：背景相同,数据相同,翻折方式不同,折痕不同.

师：你能类比问题1 提出问题并加以解决吗？

生5：我的问题是“能直接求出图2中哪些线段的长？”我的答案是：根据勾股定理可以求出BC=10,根据三角形全等与线段和差可以求出CE=6,BE=4.

生6：我的问题是“还能求出图2中剩余的线段长吗？”我的解答是：设AD=x,则DE=x,BD=8- x.在Rt△BDE中,x2+42=(8-x)2,解得x=3.所以AD=DE=3,BD=5,CD=

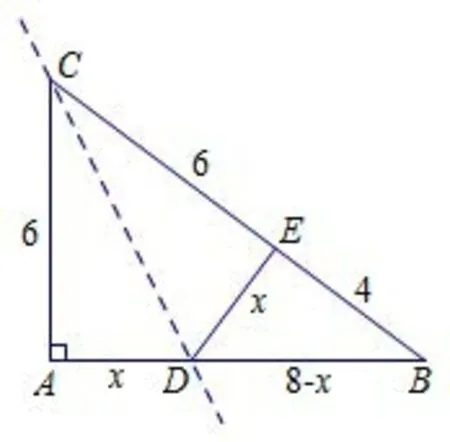
图2.1

师：你是怎么得到△BDE是直角三角形的？

生6：我是看图看出来的.

师：看出来的结论可靠吗？

生6：不一定可靠.我想到了,可以根据三角形全等证出来.因为△ACD～=△ECD,所以∠CED=∠CAD=90°,所以∠BED=180°-∠CED=90°.

师：很好.先观察图形再猜想证明是一种好方法.

为了让学生经历从直接法到间接法的思维生成过程,问题1 有意从“标已知→标可知”到“找需知→设未知”进行引导.为了让学生认识到翻折问题既要关注对应边相等,也要关注对应角相等,在问题2 的师生对话中对学生进行了追问,既肯定了学生对图形的直观感知,又完善了“观察—猜想—证明”的严谨思维,培养了学生的逻辑推理和理性思维.

三、找准解题困难,突破解题难点

为了提高解题教学效果,需要突破解题难点.突破解题难点有两层含义,首先要找准学生的实际解题困难与障碍,其次要帮助学生克服困难与突破障碍.下面对《勾股定理中的翻折问题》中两道例题的解题难点进行分析.

例1如图3,四边形ABCD是矩形,AB=8,AD=6,将 □ABC沿AC 翻折,使点B 落在点E 处,AE 与CD 相交于点F,求DF 的长.

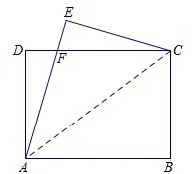
图3

师：你的困难是什么？

生1：我设DF=x,但用x表示不出AF,做不下去.

师：能否观察图形大胆猜想△ACF是什么形状？

生1：我猜想△ACF是等腰三角形.

师：能证明吗？

生1：我想到了,可以通过证明Rt△ADF～=Rt△CEF(AAS)得出AF=CF.

师：除了三角形全等的方法,还有其他方法证明△ACF是等腰三角形吗？

生2：我是从角的角度来观察的.因为AB//CD,所以∠FCA=∠CAB（两直线平行,内错角相等）.又因为∠CAB=∠CAF,所以∠FCA=∠FAC,所以AF=CF,所以△ACF是等腰三角形.

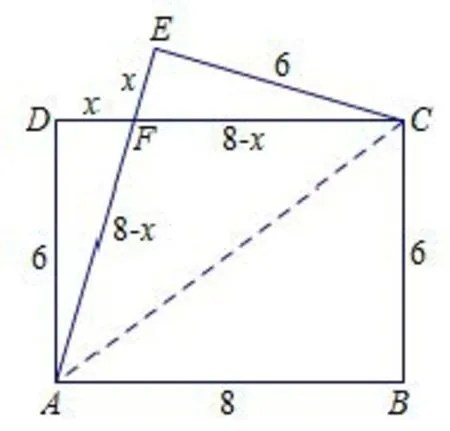
图3.1

师：接下来可以怎样求DF的长？

生3：设DF=x,则AF=CF=8-x.在Rt△ADF中,x2+62=(8-x)2,解得.所以DF的长为

师：能否进一步求出△ACF的面积？

生4：我以CF为底,AD为高,求得△ACF的面积为

师：我们来回顾一下解题过程,解题的难点是要观察出AF=CF的数量关系,突破难点的途径有两种,一是从边的角度入手,利用三角形全等得出AF=CF; 二是从角的角度入手,利用平行线关系得出∠FCA=∠FAC.由此启示我们,翻折问题既要善于从边的角度来分析,也要善于从角的角度来分析,这有助于我们打开思路.

例2如图4,四边形ABCD是边长为9 的正方形,将其沿EF翻折,使点A落在BC边上的点M处,点D的对应点为点N,若AE=5,求DF的长.

师：你能直接求出图4中哪些线段的长？

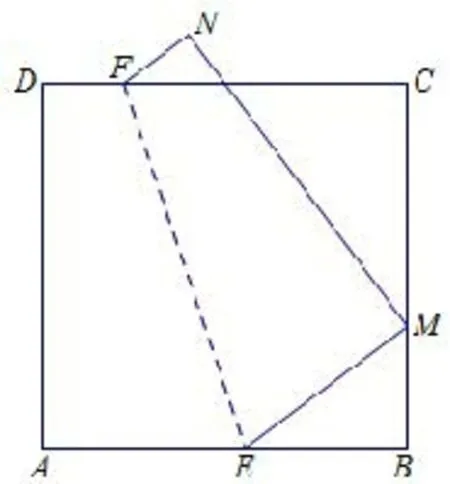
图4

生1：因为AE=5,所以ME=5,BE=4,所以BM=3,所以CM=6.因为AD=9,所以MN=9.

师：你的困难是什么？

生2：我设DF=x,则NF=x,CF=9-x,接下来做不下去.师：能否将x与9-x放在某些直角三角形中建立起它们之间的联系？

图4

生2：x可看成是Rt△ADF的边DF的长,9-x可看成是Rt△FCM的边CF的长.连接AF与FM,由Rt△AEF～=Rt△MEF(ASA),可得AF=MF,所以x2+92=(9-x)2+62,解得x=2.所以DF的长为2.

师：还有其他解法吗？

生3：x也可看成是Rt△FNM的边FN的长.由FM是Rt△FNM与Rt△FCM的公共边,所以x2+ 92=(9-x)2+62,解得x=2.所以DF的长为2.

师：这两种方法殊途同归,大家可灵活选择.能否进一步求出梯形BCFE的面积？

生4：我以BE为上底,CF为下底,BC为高,求得梯形BCFE的面积为.

师：我们来回顾一下解题过程,解题的难点是如何利用直角三角形建立起DF与CF之间的数量关系,突破难点的方法是连接辅助线AF与FM,并利用三角形全等得出AF=MF.这种连接辅助线、构造两个直角三角形、两次利用勾股定理建立等量关系的技巧,值得我们用心体会.

在以上两个例题的分析过程中,笔者根据学生的解题困难进行了有效的引导和及时的小结,既关注了学生的难点,又帮助学生突破了难点,取得了良好的教学效果.

四、回顾解题过程,提炼解题方法

解题教学的常见问题是仅停留在“就题论题”层面上,难以让学生获得解题方法与认知策略上的提升.结合具体例证来揭示问题的本质特征与提炼通用的解题策略,从“就题论题”层面提升到“由题论法”或“由题论道”的层次,应成为解题教学的重要一环.下面结合本节课的课堂小结进行分析.师：下面我们来作课堂小结.请问翻折问题的实质是什么？

生1：翻折问题的实质是轴对称,由轴对称可以得到图形全等.

师：能否用一条主线来梳理翻折问题？

生1：我的梳理是：翻折→轴对称→全等→对应边相等,对应角相等.

师：很好.能否结合本节课的解题过程用动词梳理出解决翻折问题的一般步骤？

生2：分为五步：“标→找→设→列→解”.

师：你能否解释一下这些动词的含义？

生2：“标”是指在图形中标出已知量、标出可知量,“找”是指在图形中找到全等三角形或直角三角形、找出边或角之间的数量关系,“设”是指设出未知数并用未知数表示出有关线段的长,“列”是指利用勾股定理列出方程,“解”是指解方程求出未知数并回答问题.

师：能否根据“标→找→设→列→解”说说你自己在解答各题时遇到的主要难点是什么？

生3：我的难点主要集中在“找”这一步.问题1 的难点是找到Rt△ACD并发现AD+CD=AB的关系,问题2 的难点是找到Rt△BDE并发现BD+DE=AB的关系,例1的难点是找到Rt△ADF并发现AF=CF的关系,例2 的难点是找到Rt△ADF与Rt△FCM并发现AF=MF的关系.

师：你认为在本节课用到了哪些数学思想方法？

生4：我认为在“标已知”时用到了数形结合思想,在“找关系”时用到了转化化归思想,在“列方程”时用到了方程思想.师：根据以上同学的回答,我们不妨列表小结如下.

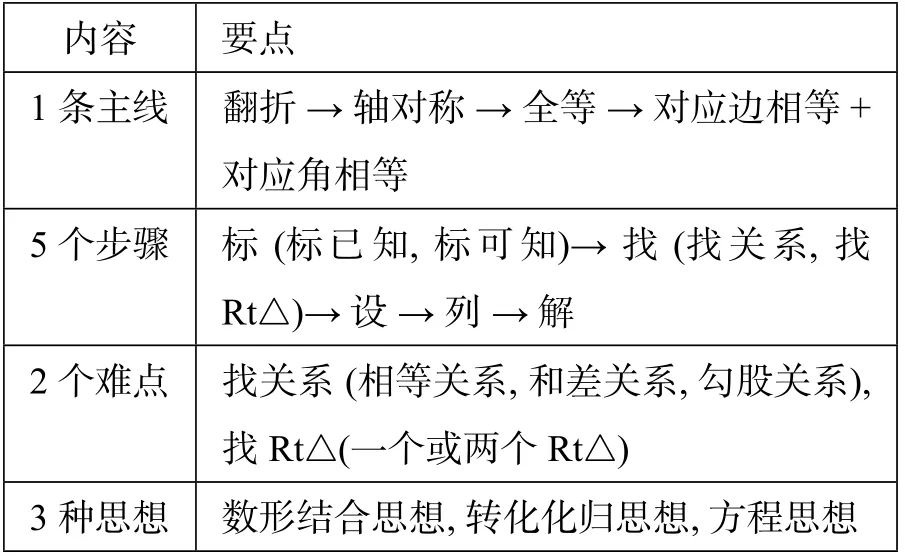
内容要点1 条主线翻折→轴对称→全等→对应边相等+对应角相等5 个步骤标(标已知,标可知)→找(找关系,找Rt△)→设→列→解2 个难点找关系(相等关系,和差关系,勾股关系),找Rt△(一个或两个Rt△)3 种思想数形结合思想,转化化归思想,方程思想

五、结语

解题教学是以问题解决为中心的教学,既要重视解决问题,也要重视提出问题.创设合适的问题情境,暴露探究的思维过程,突破学生的解题难点,提炼通用的解题方法,这些都是数学解题课的关键教学策略,值得我们不断深入实践与研究.