结合中考命题，谈初中数学函数教学

广东省佛山市三水区白坭镇白坭中学 陈坤明

初中阶段真正要求学生掌握的函数有一次函数,反比例函数,二次函数共三个函数.虽然教材里出现了三角函数的概念,但只是要求学生掌握其定义,并能运用定义进行计算,并没有要求学生学习其图像以及相关的性质,不算是要求掌握三角函数.而正比例函数它是特殊的一次函数,它的学习应该归结到一次函数之中.

虽然这三个函数的教学内容分别安排于教材里的不同地方,各函数的表达形式也差别很大,但探究其之间的联系,处理问题的方法,其实有很多地方是互通的,存在很多的共性.从教材内容编排看,对一次函数,反比例函数,二次函数的教学内容编排,大致经历了一个从函数定义与形式,到函数图像与性质,再到函数的应用的一个过程,这样的编排是符合人们对事物的认识规律的.教材内容结构有序且固定,它似乎向学生传递着学习函数该掌握的方法,似乎告诉着学生不同函数之间是紧密联系的,这有利于学生对函数整个知识结构的建立.例如判断一个点是否在函数图像上的方法、求两函数的交点坐标、求图像与坐标轴交点坐标的方法等都是相同的.

佛山市中考从2015年开始使用广东省中考试卷.翻阅2015年到2018 广东省中考试题,我们不难发现,中考对函数部分的命题有着其明显的规律,例如：这几年函数题都出现在第23 题,形式上都是一个大题里包含有三个小问.从难易分布来看,中考里大部分题目都是基础题,而拉开学生之间距离的题目有选择题的第10 题,填空题的第15、16 题,解答题的24、25 题(参考2018年广东省中考试卷),而函数题出现在第23 题,从梯度上看它位于一个从易转难的过渡位置,而且它以三个小问的形式出现,前面的两个问都比较基础,都是一些代数的计算,一般的同学都有能力解决,第3 问解题方法上没有前两问那么容易发现,需要三到四步运算才能解决,一些中层靠上的同学还是有能力完成的.从内容上看,这几年函数题都是一个直线函数与一个曲线函数结合,似乎一次函数是必考的函数之一.凸显了一次函数作为函数学习的入门函数的地位尤为重要,某种意义上决定着后续两个函数的学习,命题严格按照教学大纲的要求,科学、合理.

统计往届同学们在23 题的得分,发现同学们的得分普遍不高.进行一次教学反思,在我们的日常教学中,可能真的存在需要重视的地方,或可以进一步完善的地方.

一、加强对待定系数法部分内容的教学

利用待定系数法求函数表达式中的系数或函数的关系式,基本上是中考函数题前两个小问的必考内容.其中2015年、2018年的第三问还出现了第二次利用待定系数法解决问题,其地位的重要可见一斑.

翻开教材,待定系数法的概念,以及应用首次出现于八年级上册教材中.在第四章《一次函数》学习正比例函数,一次函数的时候已经应用到待定系数法求函数的表达式了,而待定系数法概念的出现是在第五章《二元一次方程组》中的最后一节.虽然教材编排的目的是为了突出一次函数与二元一次方程组的联系,但从某种角度上,它使得待定系数法的概念从函数的学习体系中剥离了出来,削弱了学生们对待定系数法作为函数体系内一种解决函数表达式问题的方法的整体观念,容易忽视.

在日常教学过程中,老师也往往只重视学生对结果的计算,而忽视了学生对方法本质的意义理解.待定系数法的计算是固定的,机械的,很多学生都可以通过多训练几次,多代入几次把结果正确地计算出来.但能正确计算结果未必代表学生们真正地掌握待定系数法本质,往往还会出现：对什么是系数;“系数定,函数就定”的中心思想; 到底用一个点代入还是用两个点代入等问题搞不清楚.出现了例如：已知一次函数y=kx+b的图像经过(1,5)与(-2,-1)两个点,求函数的表达式? 这样的题目会做,而对于：已知一次函数y=3x+m的图像经过(1,5),求m的值? 这样的题目反而不会做.中考对待定系数法的考察,要求学生从本质上理解待定系数法,例如：2016年的题目“在直角坐标系中,直线y=kx+ 1(k0)与双曲线相交于P(1,m).(1)求k的值; ”它要求学生能从直线y=kx+1(k0)出发,判别函数关系式中到底缺了哪个系数,需要多少个点代入.又如2017年的题目“在平面直角坐标系中,抛物线y=-x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.(1)求抛物线y=-x2+ax+b的解析式;”由于教材里习惯于在二次函数的表达式中,用a表示二次项系数,b表示一次项系数,现在用a表示的是一次项系数,而b表示的是常数,有些学生可能一时被搞混了.因此,在教学的过程中,只要我们重视让学生理解什么是系数,系数是通过把点代入表达式就可以求出的思想,问题就可以得到解决了.

二、重视平面坐标系内容的教学,特别是在平面坐标系内坐标转换部分内容的教学

平面直角坐标系可以说是函数图像的载体,而函数的大部分性质都是通过图像表现出来的.翻开教材,平面直角坐标系部分的内容被安排在八年级上册第三章《位置与坐标》,它是为下一章学习《一次函数》作准备的.

在教学的过程中,老师们可能会出现由于急于进入《一次函数》的教学,而忽视了平面直角坐标系内容的重要性,特别是第3 节关于坐标转换的内容,教材内图形较为复杂,要学习的知识点较为繁琐,老师们就更没有讲授的热情了.而对于学生而言,在学习平面直角坐标系内容的时候,由于同学们还没有学习函数的内容,未能体会到学习平面直角坐标系的意义,容易忽视了坐标转换的作用的重要了.

回顾这几年的中考题,坐标转换经常作为学生是否能运用知识解决问题的一个考点考察学生,基本上它是打开学生解决问题思路的一把钥匙,经常一个完成的解题过程,都是从一个坐标转换开始.

例如：2015年“通过直线上点A(1,3)作AB ⊥x轴于点B,交反比例函数图象于点D,且AB=3BD”,学生必须点A(1,3)与AB=3BD两个条件结合,求出D点坐标,再把D点坐标代入求出k的值.还有第3 小问“在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标”,解题的方法是做出C或D关于y轴成轴对称的对应点,再连一直线,求直线与y轴的交点来解决问题.2016年“若点Q与点P关于y=x成轴对称,则点Q的坐标为Q( )”,考察的是关于y=x成轴对称的两个点有什么关系,这样考察就更直接了.2017年的“(2)当点P是线段BC的中点时,求点P的坐标”,方法是过这个三角形的中位线,中点与其他点有何关系.

以上就是本人结合近几中考试题,总结的关于函数教学的一些看法,下面附上这几年的中考函数题,以供大家参考.

2015年

23、如图1,反比例函数y=的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB ⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.(1)求k的值;

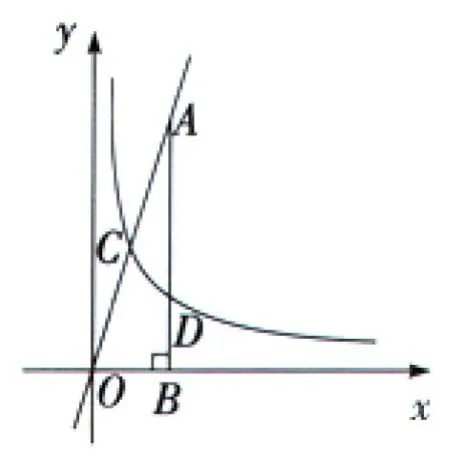
图1

(2)求点C的坐标;

(3)在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标.

2016年

23、如图2,在直角坐标系中,直线y=kx+1(0)与双曲线相交于P(1,m).

(1)求k 的值;

(2)若点Q与点P关于y=x成轴对称,则点Q的坐标为Q( );

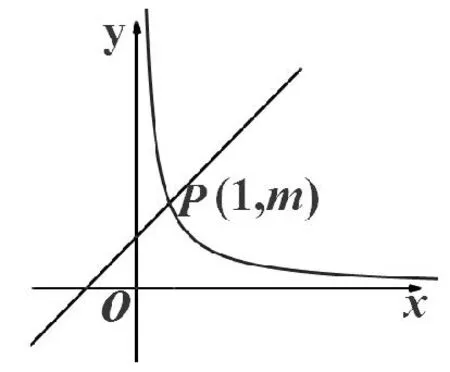
图2

(3)若过P、Q两点的抛物线与y轴的交点为求该抛物线的解析式,并求出抛物线的对称轴方程.

2017年

23、如图3,在平面直角坐标系中,抛物线y=-x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.

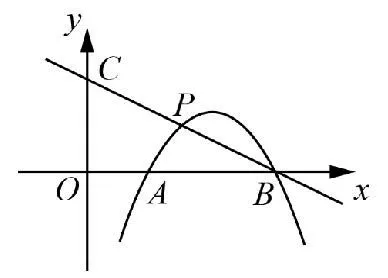
图3

(1)求抛物线y=-x2+ax+b的解析式;

(2)当点P是线段BC的中点时,求点P的坐标;

(3)在(2)的条件,求sin ∠OCB的值.

2018年

23、如图,已知顶点为C(0,-3)的抛物线y=ax2+b(a0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.

(1)求m的值;

(2)求函数y=ax2+b(a0)的解析式;

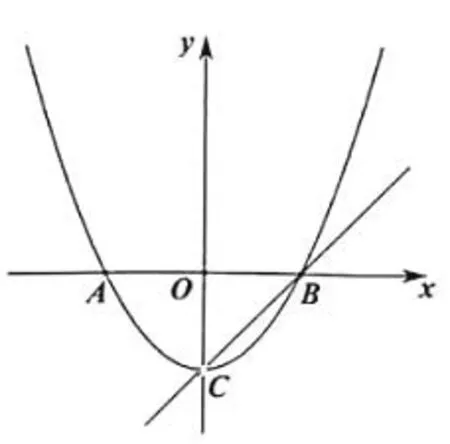
图4

(3)抛物线上是否存在点M,使得∠MCB=15°? 若存在,求出点M的坐标;若不存在,请说明理由.