数字语音扰频和解扰综合性实验设计及DSP实现

徐望明

数字语音扰频和解扰综合性实验设计及DSP实现

徐望明

（武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

设计了“DSP原理与应用”课程的一个综合性实验案例：运用数字滤波和幅度调制（AM）原理，在DSP开发平台上设计并实现了一个针对数字语音信号的扰频器和解扰器。整个设计利用Matlab和CCS开发平台完成，并进行了实验测试验证。通过该综合性实验，可使学生综合运用信号与系统、数字信号处理和通信原理等课程的知识解决实际问题，得到信号处理系统设计和实验调试等综合能力的训练。

综合性实验；DSP原理与应用；扰频/解扰；数字滤波；幅度调制

综合性实验是在学生具有一定基础知识和基本操作技能基础上，运用某一门课程和相关课程的综合知识，对学生进行综合训练的一种复合式实验，其训练内容包含多个知识点或涉及多项技术，目的是综合培养学生的实验动手能力、数据处理能力、资料查阅能力和实验结果分析能力。“DSP原理与应用”课程是电子信息类专业在高年级开设的一门实践性较强的专业课程。该课程突出信号处理基础理论（算法）和具体应用实例的工程实现。当前，DSP技术发展迅速，且DSP芯片具有处理速率高、功耗小等优点，因而应用十分广泛[1]。由于实际应用系统涉及的知识点常与多门专业课程知识相关，在实验教学中应根据实际应用场合设计相应的综合性实验项目供学生研究学习。这对提高学生综合运用所学知识解决实际问题的能力大有裨益。

日常生活中，基于DSP技术的应用系统非常多，其中一个典型的例子就是信号扰频与解扰器。比如，在电话或对讲机中配置扰频/解扰器，就可防止私人电话被窃听[2-3]；在付费有线电视系统中应用扰频/解扰器，就可对用户进行收视质量限制[4]，从而促使欠费用户缴费或让未付费用户无法正常观看。

本文以此为应用背景，结合我校“DSP原理与应用”课程教学目标和实验教学目标，以数字语音信号扰频与解扰为案例，设计相应的综合性实验项目。主要综合了信号与系统、数字信号处理和通信原理等相关专业课程的理论知识，并利用Matlab作为辅助设计工具，利用DSP集成开发环境Code Composer Studio（CCS）具体实现对数字语音信号进行加扰和解扰的处理效果。

1 语音信号扰频和解扰的原理

语音信号扰频和解扰的原理可以在模拟域进行分析。

本文设计的实验案例通过“频谱倒置”方法实现语音扰频的目的，即将输入语音信号频谱的高频部分变为低频部分，低频部分变为高频部分，并通过低通滤波器滤掉上边带信号，只传输下边带信号。下边带信号频谱正是原始语音信号频谱倒置的结果。解扰作为扰频的逆过程，原理是一样的，即扰频后的语音信号再经过一次同样的频谱搬移和滤波处理后，就可还原得到原来输入的语音信号。

由于所研究的语音信号的频率范围为0.3~3 kHz，不难通过理论分析计算出载波的频率选择应为3.3 kHz。为了实验仿真的方便，本文设计的实验案例中对语音信号扰频与解扰的实现都是在数字域进行的，即假设原始模拟的语音信号（设频带范围为0.3~ 3 kHz）已经经过A/D转换器成为数字信号。因此，只要经过一个低通滤波器（截止频率为3 kHz）将其频率限制在通带范围之内，同时利用一个正弦信号发生器产生的正弦载波（3.3 kHz）与滤波后的信号相乘，便可实现语音信号的频谱搬移。这时信号的频谱被搬移到上边带3.6~6.3 kHz和下边带0.3~3 kHz，然后再通过一个截止频率为3 kHz的低通滤波器滤去上边带信号，留下作为输出的下边带信号，该下边信号正是原始信号频谱倒置的结果，即为数字扰频信号。

如前所述，语音解扰的原理和语音扰频相同，等同于再一次的扰频。基于以上工作原理，语音扰频器/解扰器的工作原理如图1所示。

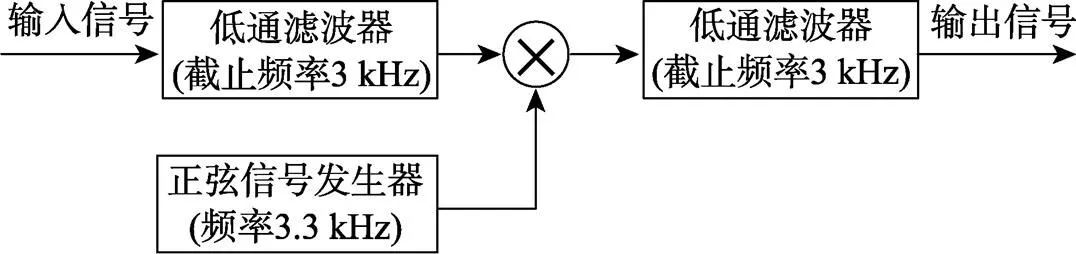
图1 语音扰频器/解扰器工作原理图

可见，本实验案例中，主要是利用信号滤波和AM调制的基本原理来实现语音扰频与解扰的功能，涉及信号与系统、数字信号处理和通信原理等专业课程基础知识。

2 数字语音扰频器/解扰器的DSP实现

2.1 低通滤波器设计

数字滤波器[7]是DSP最广为人知的应用。滤波器特性可以由通带波纹、阻带波纹、通带截止频率及阻带截止频率等参数决定。在设计数字滤波器时，必须根据这些参数来确定滤波器系数，可借助Matlab软件或专门的数字滤波器设计软件来完成[8-9]。对于DSP来说，低通、高通、带通、带阻滤波器实现程序大致相同，区别只在于滤波系数不同。实验案例中，FIR和IIR滤波器都可以满足要求，本文以FIR滤波器设计为例进行说明。

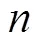
Matlab软件的数字信号处理工具箱提供了很多用于数字滤波器设计和分析的内部函数，可以通过编程方式来辅助设计；也提供了具有图形用户界面（GUI）的交互式数字滤波器设计和分析工具，可以直观方便地辅助设计，本文使用的是其中的FDATool。FDATool具有一个交互式的GUI，允许用户指定以下滤波器设计参数：

（1）滤波器类型可选择，如低通、高通、带通、带阻、多频带、升余弦等；

（2）滤波器设计方法可指定，如设计FIR滤波器的等波纹法、最小平方法和加窗法等；

（3）滤波器阶数可由用户指定，也可以是由滤波器设计方法自动确定的最小阶数；

（4）窗口技术要求仅可用于采用傅里叶方法的FIR滤波器设计，有16种窗口供选择；

（6）幅度技术要求可以是通带波纹和阻带波纹，单位可以为线性单位或dB。

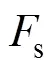
图2 利用Matlab的FDATool设计的FIR低通滤波器界面

用C语言编写滤波程序并不难，利用任何一个循环结构均可实现这种乘加运算。本实验案例中，给出滤波函数的声明如下，让学生根据所学知识编写完整的函数体：

int filter(int input,int *buf, int *lpcoefs) ; //滤波，函数声明，待实现

2.2 载波信号的产生

在数字信号处理中，经常使用到正弦信号[10]。通常的方法是查表法，即将某个频率的正弦值预先计算出来后制成一个表，DSP工作时仅作查表运算即可，主要用于精度要求不是很高的场合。若精度要求高，表就很大，需要的存储容量也要增大，此时可采用迭代法。我校开设的“DSP原理与应用”课程实验中有一个设计性实验项目，使用了迭代法产生正弦信号，可直接用于本实验案例。

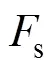
2.3 信号幅度调制（AM）的实现

为了实现对语音信号的扰频或解扰功能，使用幅度调制（AM）方法。幅度调制是用调制信号去控制高频正弦载波的幅度，使其按调制信号的规律变化的过程。对于幅度调制信号，在波形上，它的幅度随基带信号规律而变化；在频谱结构上，它的频谱完全是基带信号频谱在频域内的简单搬移[5-6]。在用DSP编程实现时，调制信号是输入的数字语音信号，高频正弦载波是利用查表法产生的正弦数据。根据本实验方案中信号的相关参数，将它们进行简单的乘法运算，根据傅里叶分析的原理，就可实现频谱搬移。再通过一个截止频率为3 kHz的低通滤波器滤去调制后的上边带信号，留下的下边带信号正是原始信号频谱倒置的结果，其输出信号即为数字扰频或解扰信号。

这部分相应的C语言程序也不难实现，函数声明如下，实验时让学生完成具体函数体的编写：

int am_mod(int input, int *sine); // AM调制，函数声明，待实现

2.4 语音扰频器/解扰器的实现

一旦学生理解了以上基本模块的原理及实现方法，再根据图1所示的语音扰频器/解扰器的工作原理图，按照“滤波—调制—滤波”的顺序组合以上函数，就能实现扰频或解扰功能。这也可以通过如下子函数进行声明，让学生实验时一起实现：

int filtmodfilt(int input); //滤波-调制-滤波（扰频或解扰子程序），函数声明，待实现

综上所述，本实验案例中用C语言编写的主程序（用于实现扰频，解扰与此类似）如图3所示。程序中，注释为“待实现”的3个子函数以及输入测试数据的初始化工作要求学生在实验课堂上补充完成。

图3 实验主程序

3 实验验证及结果分析

实验可使用TI公司的TMS320C54系列或其他系列的SDK开发板或实验箱进行，支持软件仿真（Simulator）和硬件仿真（Emulator）。TI公司提供了功能强大的集成开发环境Code Compsor Studio（CCS），可以完成源程序的编写、编译、调试和数据分析等工作。

为了便于测试和验证，实验中学生可以将设定频率的周期信号数据作为扰频器的输入，保存在数组input_signal[M]中，程序运行时不断读入其中的数据进行处理。为了便于观察，处理结果相应地保存在数组output_signal中。通过CCS提供的图形显示功能，可以查看程序运行时输入、输出的频谱图和时域波形图，观察信号扰频和解扰的效果。

以借助Matlab准备好的0.8 kHz的余弦序列（采样频率16 kHz，取一个周期的20个采样数据）作为输入信号为例，即input_signal初始化为：

static int input_signal[20] = {1000, 951,809,587, 309,0,–309,–587,–809,–951,–1000,–951,–809,–587,–309, 0,309,587,809, 951}; //0.8kHz input signal with fs= 16 kHz

此时，语音扰频器工作时的实验效果如图4所示，上排是输入余弦序列的频谱图和时域波形图，下排是受扰后输出序列的频谱图和时域波形图。

图4 语音扰频实验效果

对于输入数据是频率为0.8 kHz的余弦信号，经过AM调制后，得到双边带输出信号,其中上边带信号频率为4.1 kHz（即3.3 kHz+0.8 kHz），因其大于3 kHz而被后续的低通滤波器滤掉了，保留的下边带信号频率为2.5 kHz（即3.3 kHz–0.8 kHz），与图4中显示的结果一致。

如果再将上述扰频器的输出信号作为新的输入信号，重新运行程序，即可实现对信号的解扰，得到原来输入的余弦信号。语音解扰器工作时的实验效果如图5所示。

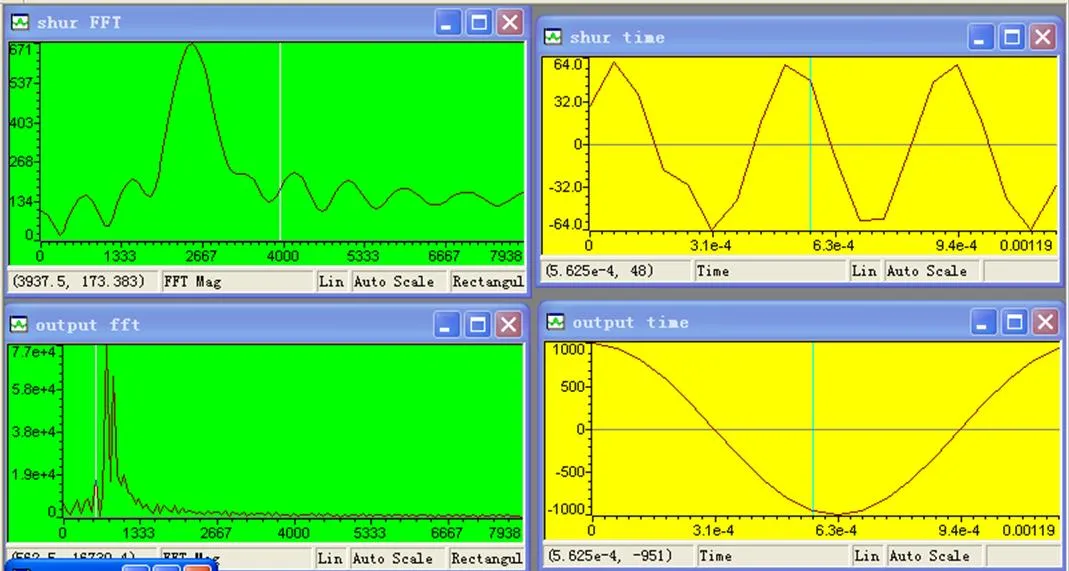
图5 语音解扰实验效果

此时的输入信号频率为2.5 kHz，得到的输出信号也是双边带信号，其中上边带信号的频率为6.8 kHz（即3.3 kHz+2.5 kHz），因其大于3 kHz而被后续的低通滤波器滤掉了，保留的下边带信号的频率为0.8 kHz（即3.3 kHz–2.5 kHz），正好是进行扰频前的输入余弦信号，成功实现解扰功能。

4 结语

利用我校DSP实验室的已有设备和条件，通过前期基础性实验，在学生掌握DSP芯片特点、功能和软件开发的基础上，进一步结合实际应用系统的特点，开发了数字语音扰频和解扰综合性实验项目。所设计的实验案例基于DSP硬件开发平台，将Matlab辅助设计和CCS 软件开发调试工具相结合，对培养学生的DSP综合设计能力很有好处[11]。另外，该实验案例把语音扰频与解扰的原理、方法与应用三者有机结合并融汇在实验教学过程中，通过综合性实验将数字信号处理及其相关专业课理论紧密联系实际加以运用，不仅有利于学生掌握方法与技能，而且能够促使学生把知识转化为能力，从而从根本上提高教学质量和 效果。

学生可以在此实验项目基础上对实验内容进一步拓展，例如：尝试使用不同的数字滤波器设计方法，使用不同的载波产生方法，使用不同的信号调制方法，并进行对比；也可开发通用的带限信号扰频和解扰实验项目；还可结合具体的DSP开发板或实验箱，利用麦克风、A/D和D/A转换电路、扬声器等实现真实的模拟语音扰频和解扰功能。此外，学生也可以根据本文实验案例的设计方法，自行研发其他综合性实验项目，用于进一步训练学生理论应用、系统设计和实验调试等综合能力[12]。

[1] 王军宁，吴成柯，党英.数字信号处理器技术原理与开发应用[M].北京：高等教育出版社，2003.

[2] 寇万里，王喆，林少锋.移动通信网络中手机防窃听语音扰频技术研究[J].数字技术与应用，2016(1): 32–32.

[3] 姜一娇.基于DSP的模拟电话保密通信装置的研究和实现[D].北京：北京交通大学，2016.

[4] 王蔻，刘裕鹏.电视信号加密技术探究[J].西部广播电视，2014(18): 159–160.

[5] 管致中，夏恭恪.信号与线性系统[M].北京：高等教育出版社，2002.

[6] 樊昌信，张甫翊，徐炳祥，等.通信原理[M].国防工业出版社，2001.

[7] 胡广书.数字信号处理: 理论、算法与实现[M]. 2版.北京：清华大学出版社， 2003.

[8] 付莉，高兴泉.基于数字滤波器的频率响应仿真实验平台[J].实验技术与管理，2016, 33(4): 119–122.

[9] RULPH C. DSP Application Using C and the TMS320C6x DSK[M]. Wiley, Hoboken, NJ, 2002.

[10] 廖柏林，王星胜，林坤，等.基于DSP正弦信号发生器设计[J].电子科技，2011, 24(2): 21–23, 29.

[11] 张卫宁，高勇.基于DSP综合应用系统的研究与实践[J].电气电子教学学报，2007(3): 106–108, 119.

[12] 高宏岩，王誉钱.基于LabVIEW和单片机的自动控制系统综合实验[J].实验技术与管理，2019, 36(1): 53–57.

Design of comprehensive experiment and DSP realization of digital voice scrambling and descrambling

XU Wangming

(School of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)

A comprehensive experiment case of the “Principles and applications of DSP (Digital Signal Processing)” course is designed. A scrambler and a de-scrambler for digital speech signal are designed and realized on the platform of DSP development based on the principles of digital filtering and amplitude modulation (AM). The whole design is completed by using the development platform of Matlab and CCS, and the experimental verification is carried out. Through this comprehensive experiment, students can use the knowledge of signal and system, digital signal processing and communication principle to solve practical problems, and get the training of comprehensive ability of signal processing system design and experiment debugging.

comprehensive experiment; DSP; scrambling/descrambling; digital filtering; amplitude modulation

TP391；G642.423

A

1002-4956(2019)10-0163-04

10.16791/j.cnki.sjg.2019.10.039

2019-02-26

武汉科技大学教学研究项目实验专项（2014Z034）

徐望明（1979—），男，湖北武汉，博士，高级工程师/高级实验师，硕士生导师，主要研究方向为信号处理、模式识别。E-mail: xuwangming@wust.edu.cn