半灌浆套筒柱中部连接预制柱抗震性能数值分析*

李英民 陈继开 王文东 王国珏

(1.重庆大学土木工程学院 400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学) 400045；3.重庆市建筑科学研究院 400045)

引言

建筑工业化是我国建筑业的发展方向，发展新的装配式结构连接方式是推进建筑工业化进程的重要举措，对于装配式混凝土框架结构来说，柱体连接的可靠性与拼装的便利性是关键因素之一。混凝土低多层框架结构在地震作用下，框架柱的最大弯矩会出现在柱端部，反弯点往往出现在柱中位置，柱中位置弯矩较小，且对于一般低多层框架结构，层高大约3m，高度约为1.5m 的柱中部位置更便于施工，考虑以上原因，对预制柱装配连接部位进行改进，将连接部位设置在柱内弯矩较小的柱中反弯点附近。其优点有：(1)装配连接部位弯矩较小，连接件的强度更容易满足要求，柱体连接可靠性增强；(2)装配连接部位远离梁柱节点区域，避开了复杂的应力集中区；(3)装配连接部位所处高度更便于施工，提高工人劳作舒适度和拼装便易性。

灌浆套筒连接方式是目前在装配式梁柱连接领域运用最为广泛的装配连接方式，针对灌浆套筒连接的数值模拟分析[1-5]均取得了较好的拟合结果。本文采用SeismoStruct 有限元软件，对已完成的试验[6]中的半灌浆钢筋套筒预制柱试件YZZ2-1 的低周往复试验进行数值模拟分析，对比数值模拟结果与试验结果来校核有限元软件SeismoStruct 的模型有效性，再建立不同轴压比下的半灌浆套筒柱中部连接预制柱和半灌浆套筒柱底部连接预制柱的有限元模型，分析对比不同轴压比下不同连接部位预制柱的抗震性能。为装配式结构柱中部连接的抗震性能提供理论参考。

1 数值模拟方法

本文首先对已完成的试验[6]中的半灌浆套筒连接预制柱YZZ2-1 的低周往复试验进行数值模拟，对比数值模拟结果与试验结果，验证SeismoStruct 数值模拟方法模拟预制柱低周往复荷载下结构响应的准确性。

1.1 试验概况

试验[6]中的灌浆套筒装配柱YZZ2-1 由地梁、上部柱身和后浇部分组成，柱高1220mm，截面尺寸350mm×350mm，配置竖向钢筋和φ8@100 箍筋，竖向钢筋在地梁与预制柱的水平接缝间不贯通，并且在地梁顶部预留相同数量的插筋，柱身底部预埋灌浆套筒，待地梁和预制柱浇筑完成并养护达到要求后起吊拼装，采用压力灌浆的方式向套筒注入灌浆料。柱顶施加265.92kN 的恒定轴压力，侧向加载装置位于柱高1025mm 处，根据《建筑抗震试验规程》(JGJ/T 101—2015)[7]的相关加载方法，试验中，在构件未开裂前由荷载控制分级加载，每级荷载大小为1kN，循环一次，接近开裂荷载时，减小级差为0.5kN，待构件开裂后，每一级荷载级差增大到5kN，循环两次；通过钢筋应变采集仪观察钢筋应变，钢筋应变达到屈服后，进行位移控制的加载方法，每级级差为6mm，正反循环两次；每一级荷载和位移加载到最大值后进行裂缝观测。当水平推力下降到峰值荷载的85%时，视为构件己经破坏，试验终止。

1.2 本构模型

1.混凝土

柱体模型中的混凝土采用Mander 非线性混凝土本构模型[8]，该模型是一个单轴非线性常数限制模型，横向钢筋也被合并到整个应力-应变范围内，因此对混凝土具有一定的约束作用。

2.钢筋

钢筋采用 Menegotto-Pinto 钢本构模型[9]，该模型是一种单轴钢模型，适用于复杂工况下明显往复受力钢筋混凝土构件。

Menegotto-Pinto 提出的本构应力应变曲线见图1，其表达式如下：

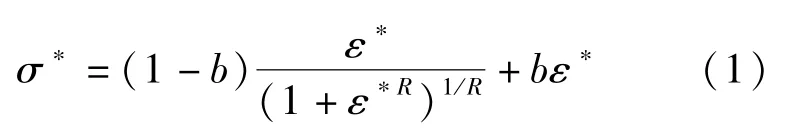
公式(1)给出的是应力应变曲线从斜率为E0的弹性段渐近线到斜率为E1的强化段渐近线的弯曲过渡过程，其中σ和ε分别为加载过程中钢筋的应力和应变，σ0和ε0分别为两折线模型中屈服点对应的应力和应变，σr和εr分别为滞回反向时对应的应力和应变。通过恒定的应变强化系数b定义钢筋的强化段渐近线，b为钢筋弹性段斜率E0与强化段斜率E1的比值。R为控制曲线形状的控制参数，在每次往复时均会变化以反应Bauschinger 效应。其表达式为：

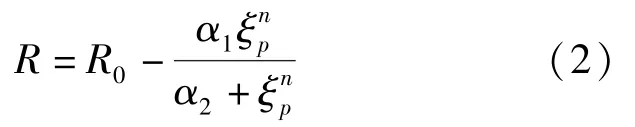
式中：R0为第一次加载时R的值；相关参数α1和α2通过材料试验确定[9]；ξnp为当前循环半周期的塑性应变绝对值。

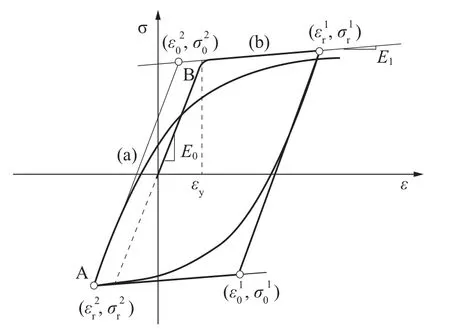
图1 Menegotto-Pinto 钢本构模型Fig.1 Menegotto-Pinto steel model

3.套筒

研究[1]表明在对半灌浆套筒装配式结构进行有限元模拟的过程中，可使用类似于钢筋等效的方法来对半灌浆套筒钢筋连接进行处理，即将套筒及其连接的两侧钢筋在一段长度内等效为一根强度略有提高、刚度减小的钢筋，强度和刚度的取值规则见公式(3)、(4)，等效后的钢筋与原套筒连接的钢筋直径相等，国外也有类似的套筒连接数值模拟的等效处理[2]，并经验证该简化方法对修正的Menegotto-Pinto 钢本构模型的钢筋模拟半灌浆套筒连接件进行低周往复加载试验有效。

套筒本构模型主要针对Menegotto-Pinto 钢本构模型进行了两点修正：

(1)修正两折线模型中的屈服应力

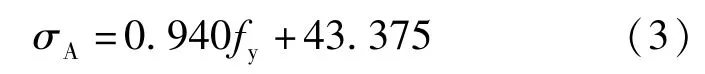
式中：σA为修正后的Menegotto-Pinto 钢本构模型中两折线模型中屈服点对应的应力；fy为连接套筒纵筋的屈服点对应的应力。

(2)修正两折线模型中的屈服应变

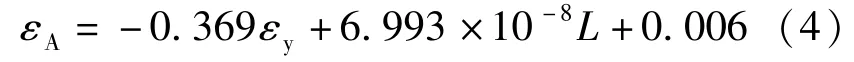
式中：εA为修正后的 Menegotto-Pinto 钢本构模型中两折线模型中屈服点对应的应变；εy为连接套筒纵筋的屈服点对应的应变；L为灌浆段长度。

1.3 单元选取

SeismoStruct 是一款基于纤维单元模型计算的有限元软件，而纤维单元可以体现截面弯矩和轴力的耦合作用，能够较好地模拟主要承受拉力的钢筋灌浆套筒在装配柱中起到的连接作用[10]。

对于截面单元的选取：侧向加载点上部柱身由于没有剪力与弯矩，故采用计算量更为精简的弹性框架截面单元(Elfrm)，加快计算收敛速度；侧向加载点下部柱身采用基于位移型函数插值的非线性梁柱截面单元(infrmDB)。

1.4 数值模拟有效性校核

模拟值和试验值对比见图2，模拟值前三级加载的承载力峰值略高于试验值；试验值最后一级加载的第二次循环构件已失效，不纳入比较。总体上模拟效果良好，可以准确地反映灌浆套筒装配柱在低周往复荷载下的力与位移关系。

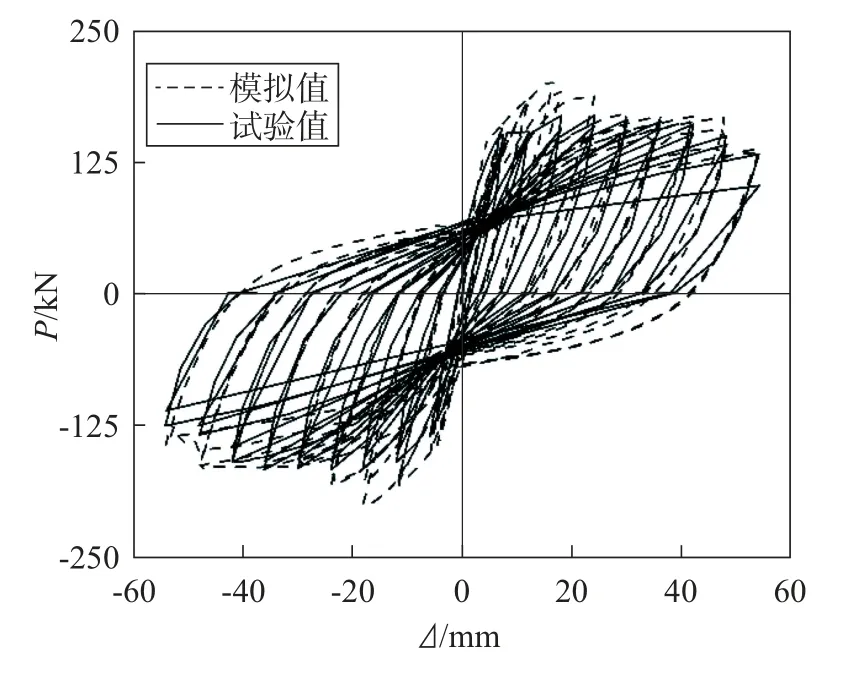
图2 滞回曲线模拟值与试验值比较Fig.2 Comparison of simulated and measured hysteretic curves

2 有限元模型建立

2.1 模型设计

采用有限元软件SeismoStruct 建立6 个数值模型，如表1所示。

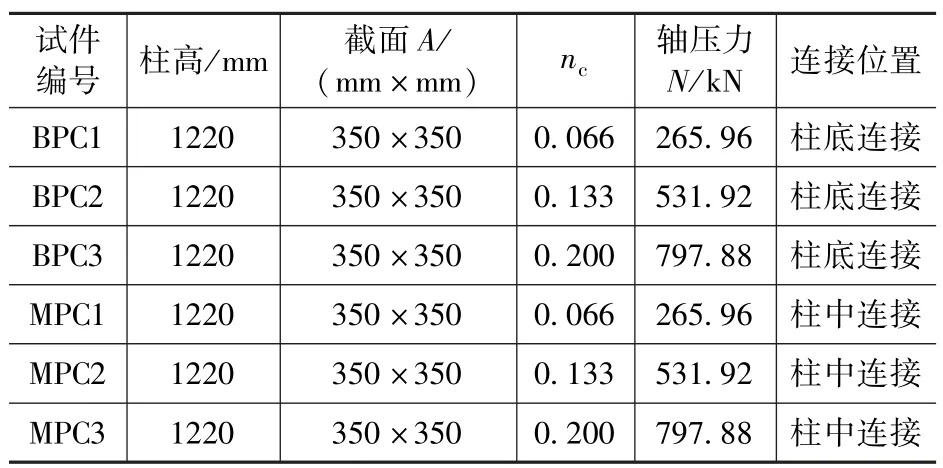
表1 试件参数Tab.1 Parameters of specimens

其中，BPC1、BPC2、BPC3 为柱底部连接预制柱，半灌浆套筒连接部位设置在柱底；MPC1、MPC2、MPC3 为柱中部连接预制柱，半灌浆套筒连接部位设置在柱中部位置。

柱底部连接预制柱与柱中部连接预制柱的几何尺寸如图3所示，柱底部连接预制柱由地梁、上部柱身和后浇部分组成，柱中部连接预制柱由地梁、下部柱身、上部柱身和后浇部分组成，柱高均为 1220mm，截面尺寸 350mm ×350mm，配置竖向钢筋和φ8@100 箍筋。

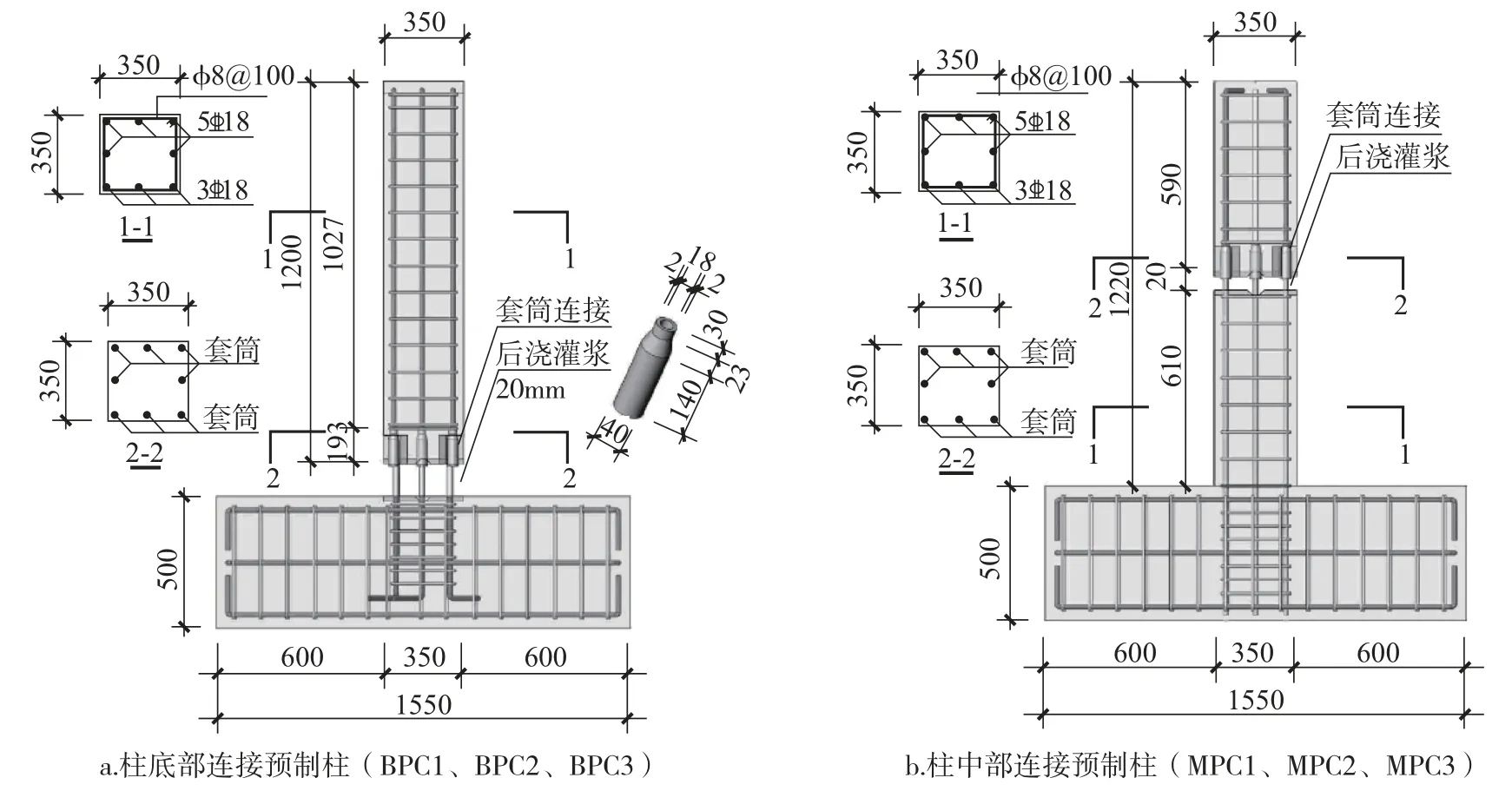
图3 试件几何尺寸和配筋Fig.3 Dimensions and reinforcement of specimens

材料参数按照试验[6]取值，试件材料具体参数见表2。

表2 材料参数Tab.2 Parameters of material

图4 有限元模型及边界条件Fig.4 Finite element model and boundary conditions

2.2 荷载设置

柱体受力模型如图4所示，柱底与地面完全约束，以一个柱底部连接预制柱模型和一个柱中部连接预制柱模型为一组，共三组，分别施加轴压比为 0.066、0.133、0.200 的恒定轴压力，在柱高1025mm 的位置设置侧向加载点，加载方式参照试验[6]的加载方案，加载位移值与试验位移值一致，每级位移加载循环两次。

3 数值模拟结果及分析

3.1 滞回曲线

滞回曲线可以直观地反应构件抗震性能，也可为后期研究构件滞回耗能、强度、刚度以及延性提供条件。

本次试验读取侧向加载点处的荷载-位移关系，各滞回曲线如图5所示。从图5可以看出，在初始弹性阶段，荷载与位移呈线性变化趋势且卸载后路径与加载路径重合，随着加载位移的增加，后一次加载曲线斜率较前一次有所下降，构件刚度逐渐下降，反复加载后，加载曲线出现反弯点形成“捏拢”，捏拢程度逐次增加。

图5 试件滞回曲线Fig.5 Hysteric loops for specimens

相同轴压比下柱中部连接试件较底部连接试件的承载力更高，滞回曲线更加饱满。

3.2 骨架曲线

骨架曲线为试件滞回曲线的各级加载第一次循环的峰值点所连成的包络线，可以反应构件受力与变形的各个不同阶段及特性。6 个试件的骨架曲线如图6所示。

从图6可知，随着轴压比增大，不论是柱中部连接试件还是柱底部连接试件，骨架曲线初始斜率增大，试件更早地进入屈服，承载力峰值点前移，曲线达到峰值点后下降更陡。

相同轴压比下，柱中部连接试件的承载力高于柱底部连接试件，这是由于半灌浆套筒连接部位作为试件薄弱环节，刚度较小，且加载过程中柱底部是主要受力部位，将半灌浆套筒连接部位设置在避开主要受力部位的柱中可以提高承载力性能。

图6 试件骨架曲线Fig.6 Skeleton curve for specimens

3.3 刚度退化

图7所示为试件在不同加载等级下刚度K随位移的变化趋势。总体上，随着水平位移的增加，刚度逐渐减小，最终趋于平稳。

分别对比三个柱底部连接试件和三个柱中部连接试件，试件的刚度均随着轴压比增大而提高。在相同轴压比下，柱中部连接试件的初始刚度大于柱底部连接试件，刚度退化更加明显。这是由于柱中部连接试件的柱底部刚度大于柱底部连接试件且在加载过程中柱底是最大受力部位导致。

3.4 构件延性

构件的延性是指从屈服到破坏的变形能力，即延性可以反应构件屈服后的变形能力。结构的延性系数越大，说明结构的塑性变形能力越强，抗震性能越好。

本文采用等能量法确定试件的屈服点，同时认为当水平推力下降到峰值荷载的85%时构件已破坏，并取该点作为破坏点。延性系数为破坏位移与屈服位移的比值。延性分析结果见表3。

表3 试件延性系数Tab.3 Displacement ductility factor of components

从表3可知，柱底部连接试件的延性系数随着轴压比增大而减小，该结果与试验[6]一致，同时柱中部连接试件也遵循该规律。

相同轴压比下，柱底部连接试件的延性系数高于柱中部连接试件。当轴压比=0.066 时，柱中部连接较底部连接延性系数高2.42%；当轴压比=0.133 时，柱中部连接较底部连接延性系数高2.49%；当轴压比=0.2 时，柱中部连接较底部连接延性系数高4.33%。

3.5 耗能性能

耗能性能是结构抗震性能好坏的重要评价指标之一，试件的能量耗散能力用试件的荷载-位移曲线所包围的面积来衡量，取6 个试件各级加载第一次循环所包含的面积作为滞回耗能，如图8a 所示，并将各级加载耗能累加得到累积耗能，如图8b 所示。

图7 刚度退化曲线Fig.7 Stiffness degradation of specimens

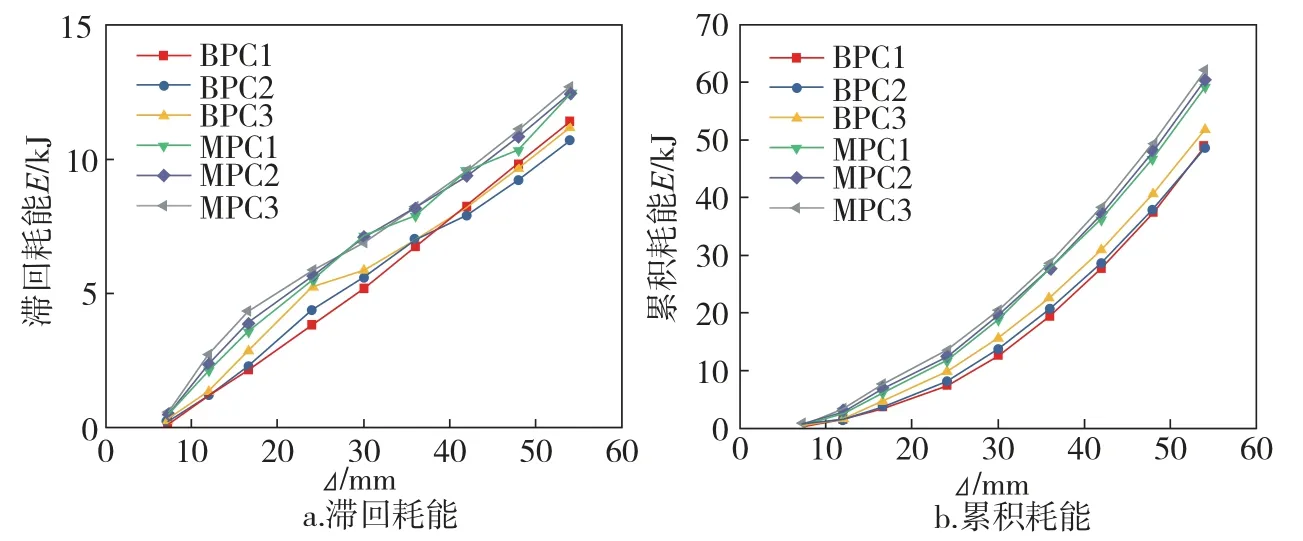
图8 构件耗能曲线Fig.8 Energy consumption of specimens

由图8可知，总体上，试件的滞回耗能随着位移的增大而增大，通过柱底部连接试件BPC1(nc=0.066)、BPC2(nc=0.133)、BPC3(nc=0.2)的对比可知随着轴压比增大，试件耗能性能增强，该规律与试验[6]得到的结果一致，同时柱中部连接试件也符合同样规律。另外，在相同轴压比下，柱中部连接试件的累积耗能大于柱底部连接试件，说明柱中部连接试件的耗能性能要优于柱底部连接试件。

4 结论

本文基于SeismoStruct 有限元软件平台，模拟了低周往复荷载作用下不同轴压比的半灌浆套筒柱底部连接试件和柱中部连接试件的受力性能，得到以下主要结论。

1.由有限元分析得到的滞回曲线与试验结果吻合良好，验证了数值模拟方法的正确性，说明了采用修正后的Menegotto-Pinto 钢本构模型的钢筋模拟半灌浆套筒连接的方法合理可行，为半灌浆套筒连接柱在低周往复荷载下的抗震性能数值模拟提供了参考。

2.随着轴压比增大，无论柱底部连接试件还是柱中部连接试件，其承载力均提高，刚度退化更加明显，延性减小。

3.相同轴压比下，柱中部连接试件较柱底部连接试件的承载力性能及耗能性能更好，延性性能略差。