看似寻常最奇崛 成如容易却艰辛——2019年高考数学江苏卷的分析与思考

江苏省徐州市第一中学(221140) 张 涛

高考试卷一经发布,各种评价纷纷接踵而来.说“试卷出的真不好,都是陈题老题”的人很多,说的铿锵有力,斩钉截铁.笔者在这里想问：你做了吗? 仔细分析了吗? 因为品味之后的数学试卷会回答：不要以貌取人,没有调查就没有发言权.认真研磨试卷我们可以这样概括它：看似寻常最奇崛,成如容易却艰辛! 就像隆冬过去,人们早已熟悉习惯枝丫枯黄,土色沧桑,但是用心生活劳作的人却知道,枯草间满是破土的新绿,老枝头满是蓄势待发的新芽.这是一份看似无意实则匠心的作品.

一、它严格、彻底地贯彻执行了普通高等学校招生全国统一考试数学科(江苏卷)的命题指导思想.

1.突出数学基础知识、基本技能、基本思想方法的考查.填空题的前10 题、解答题前两题,都紧扣教材,是考生非常熟悉的基础题,是对数学基础知识和基本技能的考查；其余的题目除了注重对基础知识的考查,又加强了对知识的内在联系和问题的分析转化能力的考查.考查中对学科主干知识如函数、三角函数、向量、立体几何、解析几何、数列等更是有所侧重.试卷涉及到《考试说明》中的绝大部分知识点,期中包括全部8 个C 级考点,38 个B 级考点中的31 个,25 个A 级考点中的9 个,贴近教学实际,既注意全面,又突出重点,分析问题、解决问题的思想与方法皆突出通性通法,注重对中学数学中所蕴含的数学思想方法的考查.

2.重视数学基本能力和综合能力的考查.数学基本能力包括空间想象、抽象概括、推理论证、运算求解及数据处理这几方面的能力,数学综合能力的考查,主要体现为分析问题与解决问题能力的考查.无疑,试卷对考生的数学基本能力和综合能力进行了全面的检测.知识、背景、方法常见的基础题体现了对基础知识和基本能力的考查,中等难度题和难题则突出体现了对考生综合能力的考查.

图1

如试卷第12 题：如图1,在△ABC中,D是BC的中点,E在边AB上,BE=2EA,AD与CE交于点O.若=,则的值是____.

本题以、为基底解决问题的初步思路实际不难寻找,但是,有一个难点不好突破,那就是点的位置.这时,就考验考生的储备和分析问题及解决问题的能力了.灵活性强或平面几何知识好的同学可以利用几何知识解决问题,而这方面薄弱些的同学也不是束手无策,可以利用书上相关习题的解决方法即利用向量共线也能解决这个问题.

3.注重数学的应用意识和创新意识的考查.数学应用意识的考查要求是：能够运用所学的数学知识、思想和方法,构造数学模型,将一些简单的实际问题转化为数学问题,并加以解决.

如试卷第18 题：如图2,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆的直径) .规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求：线段PB、QA上的所有点到点的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位：百米).

(1) 若道路PB与桥AB垂直,求道路PB的长；

(2) 在规划要求下,P和Q中能否有一个点选在D处?并说明理由；

(3) 在规划要求下,若道路PB和QA的长度均为d(单位：百米).求当d最小时,P、Q两点间的距离.

这是一道典型的实际应用问题,背景清晰明了,考查的实质是直线和圆的位置关系,但又在这个问题的基础上稍有拓展,要结合实际观察、判断并改变解决问题的方式,能充分体现出考生的数学应用意识和能力.

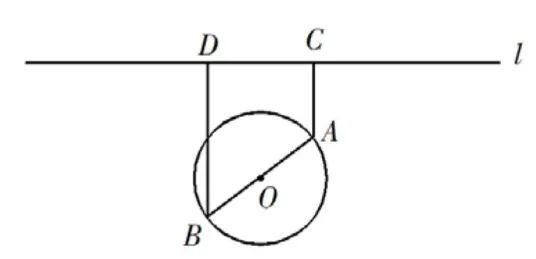
图2

数学创新意识的考查要求是：能够发现问题、提出问题,综合与灵活的运用所学的数学知识和思想方法,创造性地解决问题.

如试卷第20 题：定义首项为1 且公比为正数的等比数列为“M－数列”.

(1) 已 知 等 比 数 列{an} (n ∈N) 满 足：a2a4=a5,a3-4a2+4a4-0,求证：数列{an}为“M－数列”；

(2) 已知数列{bn} (n ∈N) 满足：其中Sn为数列{bn}的前n项和.

①求数列{bn}的通项公式；

②设m为正整数,若存在“M－数列”{cn} (n ∈N),对任意正整数k,当k≤m时,都有ck≤bk≤ck+1成立,求m的最大值.

本题前两问是对考生基本问题的解决及基本能力的考查,最后一问是考试说明中的“难题”.除了考查考生数学文字语言与符号语言的理解、转化之外,还要求考生能通过观察、猜想、验证等一系列探究活动发现线索,运用转化与化归、分类讨论等思想,构造模型解决问题.这样的考查有利于客观反映学生的学习潜能.

二、引导中学数学教学回归教材,重视基础,发展能力,提升素养,进而对日常教学产生积极影响.

1.编排合理,依纲扣本.试卷不仅在试题顺序上用心编排,从易到难,循序渐进,遵循考试心理规律,利于考生正常发挥,而且在试题内容的选择、设计上更是体现了很强的科学性及目标性.试卷紧扣《考试说明》,贴近教学实际.大部分试题来源于教材例题、习题或变式拓展,这种做法无疑有利于引导中学数学教学回归教材,也有利于引导学生夯实基础.

2.注重思想,关注素养.普通高中数学课程标准上明确数学课程目标为：通过高中数学课程的学习,学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”),普通高等学校招生全国统一考试数学科(江苏卷)的命题指导思想明确指出：命题“注重对中学数学中所蕴含的数学思想方法的考查”.2019年江苏卷很好地落实了这一宗旨,如第10、11、12、14、20 题渗透了数形结合的思想,第11、14、19、20 题渗透的函数与方程的思想,第10、11、12、14、17、18、19、20 题渗透的转化与化归的思想,第13、14、18、19、20 题所渗透的分类讨论思想等等.

学科核心素养是育人价值的集中体现,是数学课程目标的集中体现,数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.试卷对考生基本能力、综合能力、应用意识及创新意识的考查,无疑就充分表明了高考命题对考生素养的关注程度.

综合看来,知识的考查可以有效地检验高中阶段的学习效果,而思想、方法的考查则能更好地进行人才选拔,今年的试卷兼具“过关与选拔”两种功能.不仅如此,它对基础的偏重,给一线教师及备考的学子以明确方向引导,将对日常教学产生积极影响.故而,笔者认为这份试卷“看似寻常最奇崛,成如容易却艰辛”!

三、2019年高考数学江苏卷的分析后的思考.

1.教育虽现代,题海依然在,发展不变通,题海变死海.教育现代化是发展的必然,改革则是发展的必经之路.随着国家的不断发展和需要,我国基础教育经历了8 次重大改革.经过长期的教育改革,教师的教育理念和教学方式都发生了巨大变化.共同的特征是,越发突出学生的主体地位,进一步强调学生的自主学习及学为中心.数学课堂一直在悄然发生变化：预习前置让学生先学而后教,延伸课堂让学生课后继续探究,各种教学模式层出不穷……,但其中有些做法似乎偏离了数学课堂的主旨：新授课,不知不觉变成了习题课,复习课也俨然成了训练课,大量的变式题目排山倒海而来,尤其是作为高中冲刺阶段的高三,情况更加堪忧,俨然已经成了被各类教辅资料、各种纷杂试卷牵着的傀儡,终日漂浮在题海之上.

高三是基础教育的最后一年,同时又是高等教育的前一年,因此高三年级是基础教育与高等教育的分界线,也是联系基础教育,高等教育的有机桥梁.高三教学承担着双重任务,一方面对于基础教育的学习要进行梳理总结,完善提升,另一方面又要为学生进入高校学习提供必备的准备,高三的数学教学对学生的终身发展无疑是有着重要的作用.在这种关键时刻,如果我们没有有效措施和手段,因循守旧,或是做表面功夫、仅为哗众取宠,那么数学教育工作只能一步步沦为“伪教育”的俘虏,一步步退化为“单向教授”的过程,以致学生“精神”走向“被成长”.阳光明媚的日子,漂浮在题海之上的人还能有个方向,一旦风起云涌,那随之而来的就是压迫和窒息,“题海”变“死海”也是必然.这些现象非常需要我们冷静下来分析,不断分析高三数学教学现状,结合教学实践探索高三数学复习的教学策略,及时总结经验与教训,既不能一意孤行、因循守旧,也不能做表面功夫、满目浮夸.只有把这些问题真正思考清楚了,才不会曲解课改的真正含义,数学教学才有可能变得自然流畅,从而使高三数学复习教学真正回归到有序有效又有灵魂的轨道上来.

2.教育要回归本源,数学教学应回归自然.实际上,不仅是今年的试卷指向明确,近几年的试卷方向基本都很明确,江苏教育始终在努力尝试让“教育回归本源”.

人民教育出版社章建跃先生在《数学学习与智慧发展》中着重指出,全面深化课改的新要求,要回归数学教育的本来面目,着眼于学生的长期利益,发挥数学的内在力量,挖掘数学内容所蕴含的价值观资源,以提高数学素养、发展思维能力、培育理性精神为核心,使学生在掌握数学知识的过程中学会思考,成为善于认识问题、解决问题的人才.

我们期待通过研究、实践,实现高三数学复习教学朝着回归自然、真实有效的目标前进.

3.平海种树,静等陌上花开.教育的本质是帮助人成长,教学的本质是帮助人学习.“人”—教育成长的对象,是教育当然的主体,这是大自然的赋予.作为教育工作者的我们一直被称为“园丁”,而学生就是园丁身边的一棵棵树,每棵树是它自己在生长,我们所有的行动,都应是维护和促进这种生长,而不是侵入,不是拔苗助长,更不能将这些树陷入汪洋大海中.故而我们要把我们人为造出的“海”填平,还每棵树生长的沃土.树木在生长的时候,你不管什么时候去测量它的成长,都会发现很多指标的不完善,但我们隐忍不住,非得让孩子们在每个月、每段时间,都呈现出华美,于是在外力的作用下,我们所有的目标、所有的意向都集中在开花,从一年级开始,就要孩子开花,然后不停的开花,开花,……,这不是生态教育!

教育的美是什么? 是真理的探索,是生命的对话,是生长的和谐,是涌动的爱心,是交流中流淌的真诚,是师生间默契的微笑,是体验的快乐,是成功的笑容……,高三数学复习,在“任重道远”的精神指引下,老师和学生们过的忙忙碌碌,喘息不止,有谁驻足欣赏这些美,感受徜徉在身边的“阳光雨露”呢?

让路过心间的风雨,在流转不息的光阴中,随日光暖化,静等花开.