2019年高考全国Ⅰ卷理科第21题的变式与一般化探究

中山市桂山中学(528463) 蔡晓波

概率是高考中必考且重点考的知识点之一,此题一般以应用题的形式出现,能很好的考察学生的数学建模能力,数据分析能力和数学运算能力.下面笔者以2019年全国Ⅰ卷第21 题为例,通过对题目进行一般化、变式来多角度剖析该题.

一、题目再现

题目(2019年高考全国Ⅰ卷理科第21 题)为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定：对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1 分,乙药得-1 分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1 分,甲药得-1分；若都治愈或都未治愈则两种药均得0 分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.

(1)求X的分布列；

(2) 若甲药、乙药在试验开始时都赋予4 分,pi(i=0,1,···,8) 表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,···,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.

(i)证明：{pi+1-pi}(i=0,1,2,···,7)为等比数列；

(ii)求p4,并根据p4的值解释这种试验方案的合理性.

解答(1)X的所有可能取值为-1,0,1；P(X=-1)=(1-α)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β).所以X的分布列为

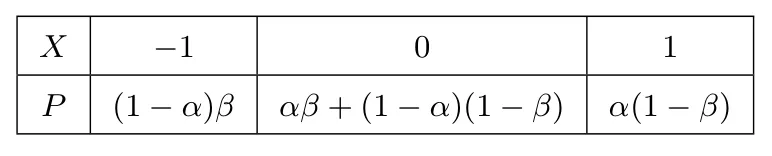
X -1 0 1_____P (1-α)β αβ+(1-α)(1-β)α(1-β)

(2) (i) 由(1) 得a=0.4,b=0.5,c=0.1.因此pi=0.4pi-1+0.5pi+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=4(pi-pi-1).又因为p1-p0=p1/=0,所以{pi+1-pi}(i=0,1,2,···,7)为公比为4,首项为p1的等比数列.

p4表示最终认为甲药更有效的概率,由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8 时,认为甲药更有效的概率为p4=≈0.0039,此时得出错误结论的概率非常小,说明这种试验方案合理.

试题评析本题在试卷中处于21 题,属于压轴题的位置,该题以测试新药为背景,解释试验方案的合理性,是一个数学应用的题目,体现了数学的应用价值,考察了学生的数学建模能力与数据分析能力.此外,本题第二问还考察了数列方面的知识,要求学生有较强的分析能力与推理能力,因此本题综合性较强,是一道考察学生数学综合能力的好题.本题难点在于：

1.题目较长,文字较多,学生需要耐心分析题目的信息.

2.提问打破常规,从以往的方案选择或者单纯的计算某个事件的概率变为利用概率解释合理性.

3.数列方面的考察也打破常规,常规的数列题目往往比较容易就能知道首项和公比(公差),而本题中数列{pi+1-pi}的首项p1-p0和末项p8-p7均不能完全知道.

二、试题的一般化与变式

(一)α,β一般化把题目中的第(2)问的“α=0.5,β=0.8 ”变为“0＜α＜1,0＜β＜1,α≠ β”,那么{pi+1-pi}(i=0,1,2,···,7) 还是等比数列吗?并求出{pn}(n=0,1,2,···,8)的通项.

解因为pi=api-1+bpi+cpi+1,且由“试题解答”(1)可得：所以0,即所以又因为首项所以是公比为首项为p1的等比数列.设由α≠β可得q/=1,所以由于p8=1,故所以所以当n=0 时,p0=0 满足pn=故pn=其中

(二)去除已知条件,弱化题目

把题目中的第(2)问的“p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,···,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8”去掉变为“0＜α＜1,0＜β＜1,α≠ β”,那么{pi+1-pi}(i=0,1,2,···,7) 还是等比数列吗?并求出{pn}(n=0,1,2,···,8)的通项.

分析由于pi(i=0,1,···,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,故pi有实际意义,因此,上述条件去除之后,我们应该也可以利用概率的知识自己求出来.

解依题意可得p0表示此时乙药已经比甲药治愈的白鼠多4 只,此时停止试验,并认为乙药有效,因此p0=0,同理可得p8=1,当i/=0 且i/=8 时意味着实验尚未停止,那么下一轮实验有如下三种情况：

①甲药未治愈而乙药治愈,发生的概率为P(X=-1),那么甲药累计得分变为i-1 分,最终认为甲药比乙药更有效的概率为pi-1；

②甲药与乙药都治愈或者都未治愈,发生的概率为P(X=0),那么甲药累计得分依然为i分,最终认为甲药比乙药更有效的概率为pi；

③甲药治愈而乙药治愈,发生的概率为P(X=1),那么甲药累计得分变为i+1 分,最终认为甲药比乙药更有效的概率为pi+1.

故有pi=P(X=-1)pi-1+P(X=0)pi+P(X=1)pi+1=(1-α)βpi-1+(αβ+(1-α)(1-β))pi+α(1-β)pi+1.以下解法与“(一)”相同.

注在该变式中,如果直接求pi比较困难,而换个角度,通过递推的思想求出了pi与pi-1,pi+1的关系,从而进一步求出pi,则问题就变得比较简单,读者可以尝试用递推的思想解决下边的这道题目：

例某个会闪烁的彩灯有红色和绿色两种颜色,第一次打开(我们约定为第1 次闪烁)时,出现红色和出现绿色的概率都是,从第2 次闪烁开始有如下规律：若前次出现红色,则下一次出现红色的概率是,出现绿色的概率为若前次出现绿色,则下一次出现红色的概率是,出现绿色的概率为；记第n次闪烁后出现红色的概率为pn,求证为等比数列,并求出pn.

(三)次数一般化

在(二)的基础上,我们把题目的2 个地方进行再次一般化：

①题目中的“当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时,就停止试验,并认为治愈只数多的药更有效.”更改为“当其中一种药治愈的白鼠比另一种药治愈的白鼠多k(k ∈N∗)只时,就停止试验,并认为治愈只数多的药更有效.”

②题目中的第(2) 问更改为：若甲药、乙药在试验开始时都赋予k分,0＜α＜1,0＜β＜1,α≠ β,那么{pi+1-pi},(i=0,1,2,···,2k-1)还是等比数列吗?并求出{pn}(n=0,1,2,···,2k)的通项.

解由(二)类似可得：p0=0,p2k=1 且pi=P(X=-1)pi-1+P(X=0)pi+P(X=1)pi+1=(1-α)βpi-1+(αβ+(1-α)(1-β))pi+α(1-β)pi+1(i=1,2,···,2k-1).结合“(一)”类似可得：{pi+1-pi} (i=0,1,2,···,2k-1)是公比为首项为p1(p1/=0)的等比数列.设q=由α≠ β可得q/=1.所以由 于p2k=1,故p1=所以pn=(n=1,2,···,2k).当n=0 时,p0=0 满 足所以其中

注读者可以思考,为什么题目中甲药、乙药在试验开始时都要赋予k分,能带来什么样的便利.

(四) 结论变式

在(三)的基础上,我们增加一问：若α=0.5,β=0.8,且要求出错概率不超过,则k的最小值是多少?

解：因为α=0.5,β=0.8,所以根据(三) 可得：q==4,所以pn=(n=0,1,2,···,2k).pk相当于实验还没开始或者实验虽然进行了但甲药与乙药的有效次数一样多,并且甲药治愈率α小于乙药治愈率β,因此出错概率不超过等价于pk＜,所以pk=又因为k ∈N∗,故可得k ≥5,故k的最小值为5.

注在此变式中,若将“α=0.5,β=0.8 ”修改为“α=0.8,β=0.5”,那么又该怎么做呢? 留给读者自己去思考.

三、小结与反思

此题实际上是一个优胜劣汰的问题,其实相当于对弈问题中平局概率不为零的情况,在教学中,教师可以通过变换题目背景,训练学生的数学建模能力.

由2019年全国Ⅰ卷的概率题目,我们不难发现,该题考察面较广,突破了该题仅考概率与统计知识的常规,偏向于跨知识点的运用,注重考察学生的逻辑推理、数学建模、数学运算、数据分析等方面的能力.

因此,教师在教学中,可以通过一题多变引导学生对问题进行深层次的思考.