新型考虑短板效应的客船应急疏散路径模型*

马全党 谭恒涛 刘 森 苏 昂 谢 娜

(武汉理工大学航运学院1) 武汉 430063) (武汉理工大学能源与动力工程学院2) 武汉 430063)

0 引 言

近年来由于客船事故频发，严重影响客船旅游业的发展[1].通过研究近年来多起水上交通事故发现，疏散秩序和路径选择是应急疏散的关键因素[2]，国内外学者对此进行了广泛研究.吴祖新等[3]提出的灰色变权聚类模型；林国龙等[4]提出的元胞运输模型；赵星等[5]提出的疏散网络优化双层模型；刘红等[6]提出的当量长度疏散模型.以上研究方法特点各异，但在时效性和适用性上均有所欠缺，具体见表1.

表1 疏散模型特点及缺陷

客船应急疏散指乘客从警报发出到离开船舶的全部过程，主要包括两个阶段：“准备”阶段，乘客到达指定逃生点，通常为乘客登上救生筏或进入逃生滑道的地点；“逃离”阶段，即从逃生点疏散到安全点的过程.文中主要研究“准备”阶段的疏散行为，并针对客船人员疏散过程中的短板效应，即疏散效率最低的区域决定客船总体疏散效率，提出了一种全新的通道及路径通行难度整合方式，并结合客船结构及其工作环境的封闭性与特殊性，构建了一种新型客船应急疏散路径模型，可充分体现通行短板因素的影响，并通过分析仿真实验过程进一步优化模型参数，有效防止短板效应造成的误差，对于客船应急人员疏散路径模型的研究及应用具有重要的参考意义.

1 建立优化疏散路径模型

1.1 模型假设

准确评估各通道通行状态是实现最优路径规划、成功疏散遇险人群的基础[7].由于客船工作环境和内部结构的独立性和相对封闭性，客船人员应急疏散过程中存在以下两个对应特征：①多数通道普遍存在障碍因素，即通行受阻；②局部通道可能存在危险因素，即无法通行.据此，为在降低模型复杂度的同时保证其准确性，现作出以下假设:

1) 疏散网络中任一通道均可能存在通行障碍因素及危险因素，但至少存在一条通向疏散点的完整路径.

2) 疏散引导可有效消除人员个体差异及心理因素对其行为的影响，在疏散过程中所有待疏散人员均遵循系统引导进行疏散.

3) 节点与通道存在通行容量限制，其疏散点不存在容量限制.

4) 在任一时刻，通行障碍因素致使通行难度系数达到一个较大值时，或疏散网路上某通道危险因素达到明确危及生命的阈值，视该通道为瘫痪状态，人员无法通行，后续疏散路径不得包括该通道.

5) 疏散过程中不允许人员在两节点间往返运动.

1.2 通行难度评估

在普遍的疏散研究中，杜红兵等[8]指出，人群的疏散在通道受阻的场景下存在木桶短板效应，严重影响了疏散的秩序及效率.在对客船疏散路径模型的研究过程中发现，客船人员应急疏散也存在一个类似的效应且容易被忽略，称之为通道短板效应，即疏散效率(流量)最低的区域决定总体疏散效率.例如，对于流量“1”+“7”“2”+“6”“3”+“5”“4”+“4”等组合，其整体流量大小主由较小的“1”“2”“3”“4”决定.

而在客船疏散路径规划中，这种效应有两个表现形式:①单个通道内各种通行障碍因素对该条通道的流量的影响反映，即在客船上层建筑的任一通道中，各种障碍因素对该通道流量的影响大小不一，而由障碍系数最大的障碍因素主导，对于单一通道风险及通行难度(流量)评估有着重要的参考意义；②各个通道的流量对路径整体流量大小的反映，即将多个通道组合规划成一条完整路径时，通常主导整体路线流量大小的是流量最小的那条通道，对于多通道组合的路径整体通行难度(通行所需时间)有着不可忽视的影响.

1.2.1单一通道内通行难度评估

由于客船内部结构和外部工作环境的特殊性，考虑的典型通行障碍因素包括船体倾斜、人群拥堵及火灾.

目前通道内障碍因素的通行难度的整合为

(1)

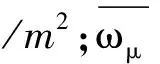
但使用这种整合方式，障碍系数大的因素对通道通行难度系数的影响很可能被多个障碍系数小的因素的影响淡化，难以形成明显的区分度，忽视了短板效应在通道通行难度系数评估中的作用.针对这个问题，提出一种新的整合方式，为

(2)

式中：ri为通道倾斜因数；μ为通道内人群密度，人/m2；fi(Kc)为减光系数对人员速度的影响系数；fi(ρCO)为一氧化碳对人员速度的影响系数；fi(Ts)为烟气温度对人员速度的影响系数；Ii为任一通道当量长度；Iij为任一通道实际长度，m.

当客船船体倾斜时，人群移动速度v会减小[9]，其修正表达式为

v=v0ri

(3)

式中：v为船体倾斜时的人群移动速度人群移动速度；v0为船体未倾斜时的人群移动速度；ri为通道倾斜因数.其中ri的计算方法具体为

(4)

(5)

(6)

(7)

(8)

式中：ri为倾斜因数；r1，r2为走廊横向、纵向的倾斜因数；r3为楼梯横倾因数；r4，r5为楼梯纵倾时上行、下行因数；φ为倾角(横倾时右倾为正、左倾为负;纵倾时首倾为正、尾倾为负).

当通道内人群密度到达一定程度时，极易发生拥堵、停滞，导致人群移动速度下降[10]，为

v=-0.052μ3+0.396μ2-1.07μ+1.311 (9)

式中：μ为通道内人群密度，人/m2.

王绍晓[11]经过研究得出减光系数对人员速度的影响系数表达式为

(10)

式中：Kc为减光系数，1/m.

CO对人员速度的影响系数计算公式为

(11)

式中：φCO为CO的体积系数，%；t为人接触CO的时间；f2(φCO)=0为人员出现生命危险，通道禁行.

Milke[12]认为烟气温度对人员速度的影响系数为

(12)

式中：θs为火场温度；v0为初始移动速度.

式(2)的整合方式可明显扩大障碍系数较大的因素的影响，并防止被障碍系数较小的因素淡化，同时体现小尺度空间范围内各障碍因素之间的叠加效应.为体现疏散过程中不同大小的障碍因素对通道当量长度的影响，特参考实际情况选取三组不同的障碍因素组，通过计算得出三种情况的当量长度对比见表2.

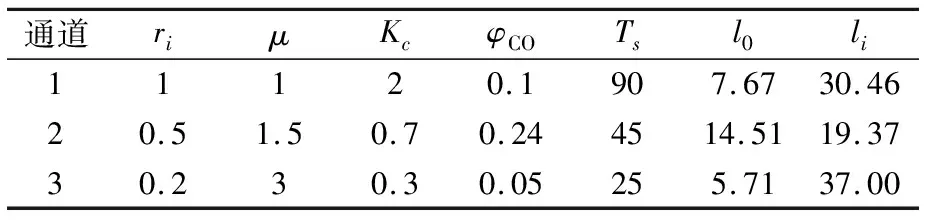
表2 通道当量长度整合对比表

1.2.2多通道整体通行难度评估

在对单一通道内通行难度系数评估的基础上，基于图论思想对包含多条通道的整条路径进行整体通行难度系数评估，以此作为路径规划的主要参考依据，但传统的将各通道通行难度组合叠加的方式忽视了短板效应的重要影响，常给出“1”+“7”=“2”+“6”=“3”+“5”=“4”+“4”的通行难度拟合结果，与路径实际通行难度形成明显偏差，难以为后续的路径规划提供有效的数据支撑[13-14].而这种源头上的缺陷往往无法通过算法减小或消除，也就无法规划出真正意义上更“短(通行用时)”的疏散路径，故文中提出一种新的整合评估方式，为

(13)

式中：Li为任一疏散路径当量长度；Ii为任一通道当量长度.

以式(13)为基础构建的客船应急疏散路径模型，可较好的反映通道短板效应对疏散路径的影响，更符合客船通道的实际情况.

选取三张通道当量长度为例，传统整合方式得出的路径当量长度L0与新型整合方式得出的路径当量长度对比见表3.

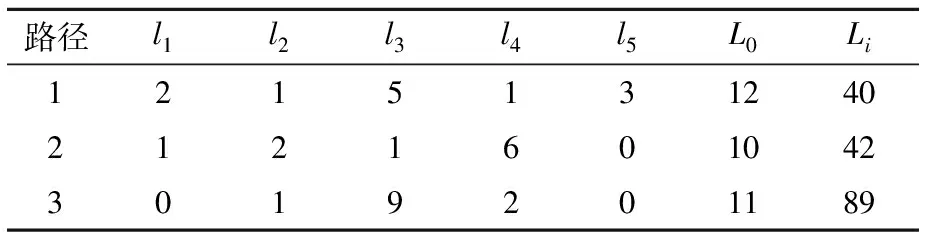
表3 路径当量长度整合对比表

2 模拟疏散仿真

基于Visual Studio开发平台对系统的疏散逃生效果进行计算，选择实验船舶第三层为典型案例对该层人员分布和移动进行网格化建模分析，设置每个人所占面积为0.5 m×0.5 m，不可重叠.基于上述优化疏散路径模型，在实验船型上进行模拟仿真实验，设定各舱室人员，设定一小倾角，并在通道中设置若干通行障碍，观察分析模拟仿真疏散过程，进一步优化模型参数.具体流程见图1.

图1 仿真实验流程

2.1 实验船舶参数

选用与“东方之星”号参数相似的姊妹轮船作为仿真实验模型，其具体参数见表4.

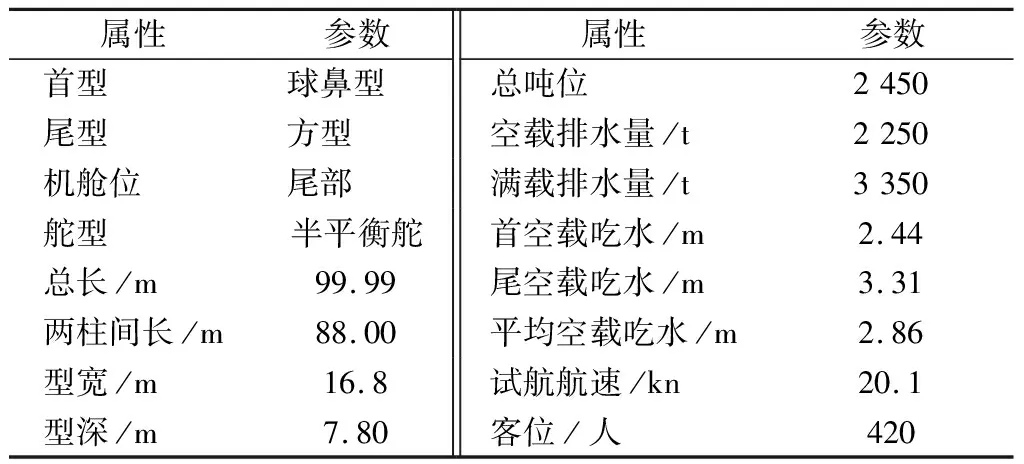
表4 实验船舶参数

2.2 实验初始条件设定

船舶第三层总长80 m，总宽15 m，横向走廊宽1.5 m，纵向走廊宽1.5 m，中厅尺寸为12 m×16 m，各房间尺寸均为4 m×7 m；在通道中设置若干危险因素与障碍因素，设定船体横倾角度为10°；三等舱每个房间4人，二等舱每个房间3人；人物所占网格面积为0.5 m×0.5 m，人员的移动均视为横向—纵向移动，移动过程中人员所占网格不重叠.初始状态见图2.

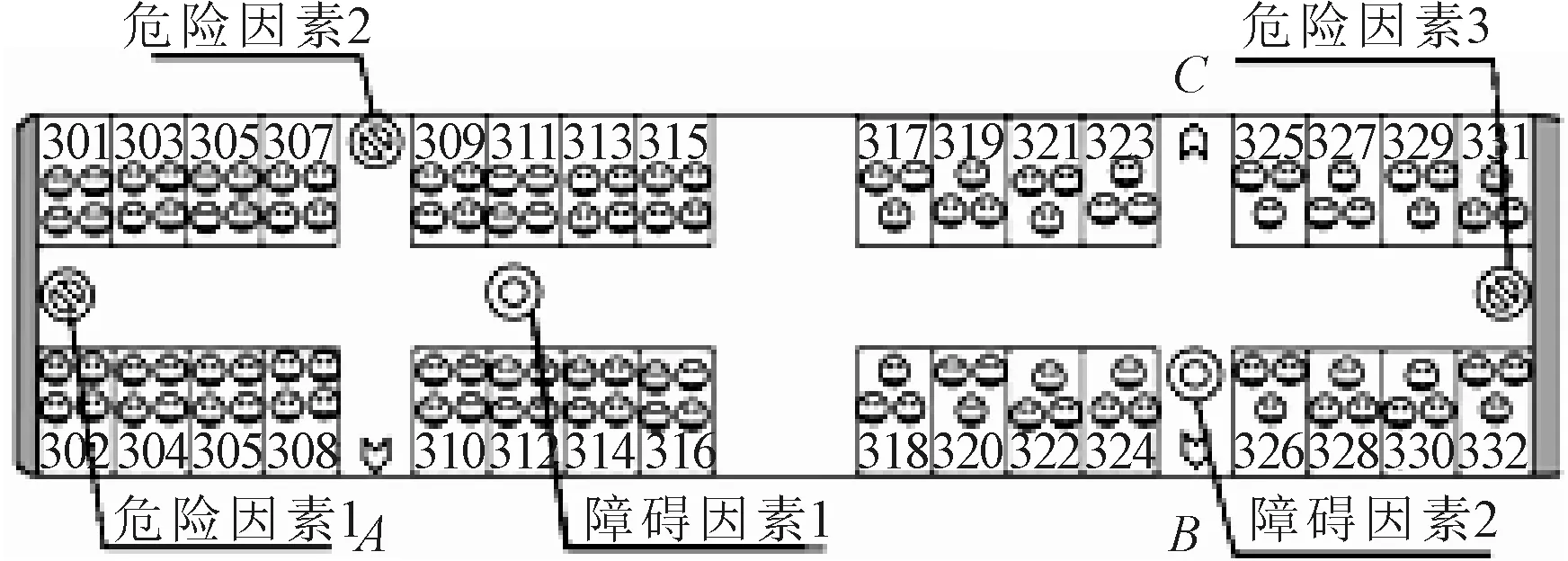
图2 仿真初始状态图

假设船舶第三层发生火灾，其中危险因素1与危险因素2设置为φCO=0.3，即该处因一氧化碳气体浓度过高而不能通行；危险因素3设置为θs=90 ℃，即该处因火场温度过高而不能通行；障碍因素1设置为φCO=0.12，即该处因CO气体浓度升高阻碍乘客疏散；障碍因素2设置为减光系数Kc=0.6，即该处因为烟雾造成能见度降低阻碍乘客疏散.

2.3 初始仿真

疏散过程见图3，疏散开始9.2～35.4 s，房间内人员分批依次跑出，进入横向—纵向通道；在38.5 s左右，全体人员均进入通道进行疏散，且各自选定逃生出口并确定疏散路径，但三个出口的人员分别相差较大，A出口人员很多疏散效率偏低，而B出口处人员很少疏散较快但后期处于空闲状态，疏散资源分配不均.260 s左右B出口处人员已疏散完毕，330 s左右C出口处人员也成功疏散，但A出口处仍有10人左右还在出口前，最终在392 s左右才完成.即使立即改变疏散路径调整人员分配此时转而从B或C出口疏散出来也只会花费更多的时间，因此只能按原定路径进行疏散.

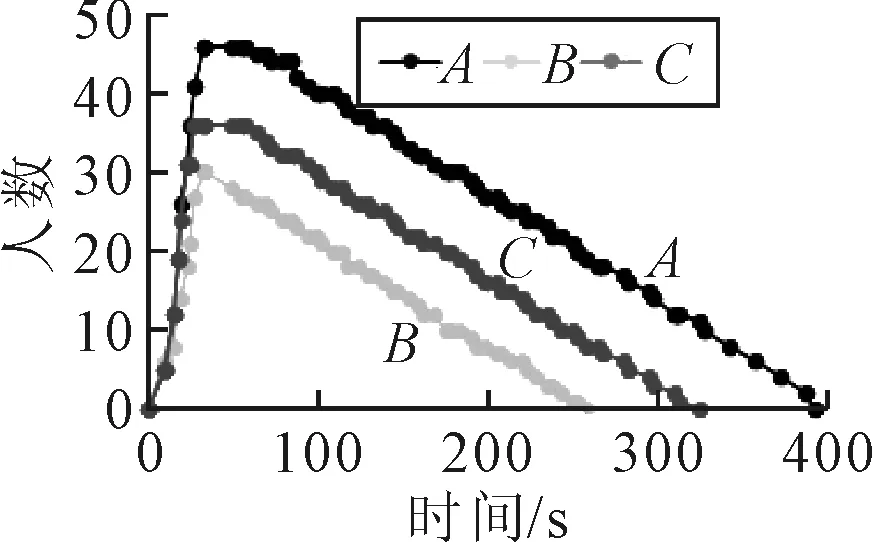
图3 初始疏散过程

整体疏散情况见图4，由图4可知，疏散整体流程较为平缓，前期响应迅速，中期疏散较为顺利，但是后期(即260 s之后)因为人员分布和资源调控不均导致整体疏散效率明显下降.

图4 初始疏散整体效果

2.4 优化仿真

分析发现，人员在各出口处须排队登上救生艇、筏或转移到安全地点，而这个流程所需时间为10 s，此时整个疏散队列缓慢移动，以网格法换算，每10 s移动一个网格可视为0.05 m/s.而这种移动速度在疏散过程中可视为通道完全拥堵无法通行，即这种状态实际上是出现的概率极小且不会持续存在.若在此时仍以人群密度作为疏散通道的通行影响指标，则极易产生错误判断，致使人员分配与疏散资源调控不对称，导致整体疏散效率降低.

综合考虑，此时更应直接将人员分配作为主要因素考虑，为消除人群密度对疏散效率的过度影响，对照式(2)进而将通道的当量长度调整为

(14)

并进行进一步的仿真实验验证.

系统输出结果见图5～6，疏散路径模型优化后的模拟疏散过程，各出口处的人员分布更为均匀，疏散资源的调控也比较合理.各出口处人员疏散完成时间间隔较小，B、C出口处人员疏散在320s左右完成，A出口处的人员疏散在356s左右完成，有效的提高了出口的利用率，较大程度上减少了不必要的时间冗余，使整体疏散过程顺利、平缓.

图5 优化疏散过程

图6 优化疏散整体效果

从仿真实验开始到全部疏散完毕，共用时356s，考虑船上人员个体差异及相互之间的影响，取25%的时间富余量，即船上人员疏散过程所需时间为445s.外加上应急反映时间2.5min，全部人员疏散到指定集合地点只需10min，在指定地点登艇或其他救生设备专业需要10min，总计20min完成整个疏散过程.与现阶段的研究成果及疏散演习的效率相比(见表5)，显著提高了客船人员应急疏散的效率.

表5 疏散效果对比

仿真结果表明，对疏散路径模型的优化符合客船人员疏散的特点，且具有较好的适用性与稳定性，与现阶段的应急疏散相比，可有效提高客船人员应急疏散效率，对于客船应急疏散的研究具有重要的参考意义.

3 结 论

1) 针对通道短板效应在客船应急疏散中的存在形式，对任一通道的通行难度和整体路径的通行难度均提出新的整合方式，构建了一种新的客船疏散路径优化模型，可有效消除短板效应造成的偏差，提高疏散路径模型的适用性.

2) 选取实验船型，基于Visual Studio开发平台进行仿真疏散模拟实验，通过观察分析疏散过程，将人员分配作为主要因素考虑从而进一步优化模型结构与参数，提高了疏散路径模型与客船实际情况的契合度.

3) 该疏散路径模型在各因素的权重参数分配上仍有提升空间；而如何在疏散模型精度与计算时效性之间找到一个更优的平衡，则是该模型能否在客船人员应急疏散中普遍应用的关键指标.以上也将作为后续研究的重点.