基于单直角电桥的交流电阻校准装置测量不确定度评定
李亚琭 张国强 胡志远
(北京东方计量测试研究所,北京 100096)
1 引 言
交流电阻计量技术在很多领域有着广泛的应用,如在通信领域中,通常要采用宽量程和宽频率范围的交流电阻标准对通信设备进行校准;在元器件制造应用领域中,对交流电阻的准确定值有助于提高元器件的质量和准确度;在电力控制领域中,通过对电网电线的交流电阻量值的准确快速测量,可以准确快速的调整调节装置,防止电网发生震荡[1];在电化学领域中,交流电阻的特性可用于对电极过程、金属腐蚀等现象的研究;在热力学领域中,交流电阻标准是热力学绝对温标的三大支柱之一;此外感抗、容抗的单位也都是欧姆,把电容标准、电感标准溯源到电阻单位上的过程中,交流电阻起到了核心作用。综上所述,交流电阻的计量在国民经济、科技发展、工业生产等方面中均有着重要作用。
本文基于单直角电桥的原理,利用自主研发的数字式直角电桥源作为双路正交电压信号的输出,搭建了交流电阻校准装置,并对整个装置进行了测量不确定度的评定。根据单直角电桥的原理,当电桥平衡时建立了被校交流电阻的数学模型,分析了测量不确定度的主要来源;并对交流电阻的各个测量不确定度分量进行了计算,采用不确定度传播公式对其进行合成,通过扩展得到整个校准装置的测量结果与扩展不确定度。
2 单直角电桥的原理
目前国际上对于交流电阻的溯源采用的方法主要有通过感应分压器电桥将交流电阻溯源至交流量子化霍尔电阻[2,3];通过交、直流差可计算电阻和时间常数进行溯源;通过直角电桥将交流电阻溯源至可计算电容[4]等。其中直角电桥主要用于非同类阻抗的比较测量,它是将两个相互正交的交流信号分别通过待测交流电阻和标准电容,使电桥达到平衡。若能输出两路幅值相等,相位相差90°的正弦电压波形,则可根据单直角电桥的平衡方程将交流电阻溯源到电容标准上。最简单的直角电桥如图1所示。该电桥是具有90°相位差的直角电桥,构成电源比例臂的两个电动势U和jU幅值相等,相位差为90°[5,6]。
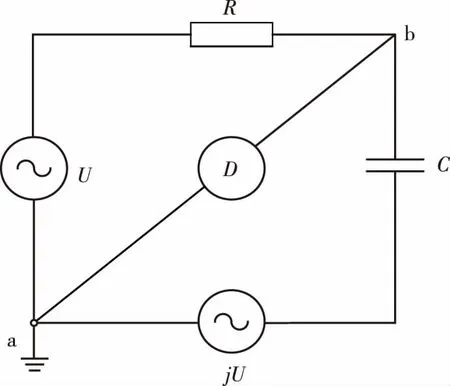
图1 单直角电桥原理图Fig.1 Single quadrature bridge schematic
图1中,当指零仪D示数为零时,则a,b两点处的电势相等,电桥达到平衡,此时图中b点电压Ux为
(1)
式中:Ux——b点处电压,单位:V;U——单直角电桥电路中电压源的电压幅值,单位:V;jU——单直角电桥电路中正交电压源的电压幅值,单位:V;R——直角电桥电路中交流电阻的阻值,单位:Ω;C——直角电桥电路中标准电容的标准值,单位:F;ω——直角电桥电路中电源角频率。
由于电路中Ux电压与电源电动势正交,即
Ux=-jU
(2)
则根据等式两边虚部实部分别相等,可得
(3)
(4)
可得关系式为
ωCR=1
(5)
如此可见,只要能够得到高准确度的电源角频率,便可求出电阻R和电容C之间的比例关系,并且可以达到较高的测量准确度[7]。本文采用单直角电桥原理,搭建了交流电阻校准装置,通过直角电桥将交流电阻溯源至标准电容上。利用电桥平衡方程,便可通过电容的标准值间接地计算出待测交流电阻的阻值。
3 交流电阻校准装置构成
本文利用上述所述的单直角电桥原理,使用自主研制的数字式直角电桥源作为双路正交电压信号的输出,搭建了交流电阻校准装置,其校准装置如图2所示。

图2 交流电阻校准装置示意图Fig.2 AC resistance calibration device diagram
根据前面所述,当电桥达到平衡时,流经相角电压表的电流为零,假设两路交流电压输出的幅值完全相等,直角电桥的平衡方程参考式(5)。但在实际情况中,直角电桥的双路交流电压输出无法做到幅值和相位完全一致,存在一定的误差,因此在实际测试中不能忽略幅值差和相角误差的影响。设两路幅值相等、相位相差90°的正弦交流电压U和jU分别为Ua和Ub,则可表达为
Ua=U,Ub=KUej(90°+Δθ)
(6)
式中:U——正弦交流电压Ua的幅值;K——两路正弦交流电压Ub与Ua的幅值比例;Δθ——两路正弦交流电压相角的实际差。
设交流电阻和标准电容的表达式为
(7)
则当电路平衡时,相角电压表中无电流通过,应满足
(8)
将交流电阻、电容、交流电压源Ua,Ub的表达式带入式(8)得
(9)
因此,得到交流电阻的阻值为
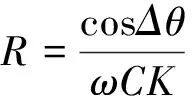
(10)
4 测试数据处理
根据数字式直角电桥交流电阻计算公式,在不同的频率下选择不同的标准电容,就可将交流电阻量值溯源到电容标准上[8],选取的测试点和测试数据见表1。

表1 交流电阻校准装置测试数据Tab.1 AC resistance calibration device test data测量频率点实测频率/Hz标准电容标称值标准电容证书值交流电阻标称值交流电阻测量值100Hz99.949 8531μF0.999 9μF1.591 55kΩ1.592 50kΩ100Hz99.980 550100nF99.992nF15.915 5kΩ15.919 9kΩ100Hz99.944 84610nF9.999 8nF159.155kΩ159.246kΩ159.155Hz159.114 501μF0.999 9μF1kΩ1.000 35kΩ159.155Hz159.134 46100nF99.992nF10kΩ10.020 9kΩ159.155Hz159.229 4110nF9.999 8nF100kΩ99.955 2kΩ159.155Hz159.081 581nF0.999 84nF1MΩ1.000 6MΩ1kHz999.895 511μF0.999 9μF159.155Ω159.188Ω1kHz999.394 73100nF99.992nF1.591 55kΩ1.592 61kΩ1kHz999.395 1210nF9.999 8nF15.915 5kΩ15.925 5kΩ1.591 55kHz1588.642 31μF0.999 9μF100Ω100.193 0Ω1.591 55kHz1591.042 2100nF99.992nF1kΩ1.000 40kΩ1.591 55kHz1591.712 410nF9.999 8nF10kΩ9.999 2kΩ10kHz9965.951 1100nF99.992nF159.155Ω159.711 5Ω
5 测量不确定度分析
由上述构建的交流电阻校准装置,在频率1.591 55kHz、幅值有效值1V下,以标准电容100nF,交流电阻1kΩ为测试点,进行了测量不确定度分析。
5.1 建立数学模型
对于交流电阻校准装置,其测量结果的数学模型为
Δ=Rx-R0
(11)
(12)
(13)
式中:Δ——交流电阻的误差,单位Ω;Rx——交流电阻的实际测量值,单位Ω;R0——交流电阻的标准值,单位Ω;f0——直角电桥源频率的标准值,单位Hz;C0——标准电容器的标准值,单位F;K——数字式直角电桥源通道2与通道1的比值,单位1;Δθ——数字式直角电桥源两通道输出90°波形时的相位误差,单位(°)。
交流电阻测量结果的不确定度传播可用式(14)表示
u2(Δ)=c2(Rx)u2(Rx)+c2(R0)u2(R0)
(14)
其中,灵敏系数为
c(Rx)=1,c(R0)=-1
式中:u(Rx)——交流电阻测量值引入的标准不确定度;u(R0)——交流电阻标准值引入的标准不确定度。
其中,u(R0)按式(12)表示为
u2(R0)=c2(f0)u2(f0)+c2(C0)u2(C0)
(15)
其中,灵敏系数为
(16)
式中:u(f0)——直角电桥源频率的不准确引入的标准不确定度;u(C0)——标准电容的不准确引入的标准不确定度。
u(Rx)按式(13)表示为
u2(Rx)=c2(Δθ)u2(Δθ)+c2(K)u2(K)
(17)
其中,灵敏系数为
(18)
(19)
交流电阻标准值R0引入的相对标准不确定度ur(R0)为
(20)
交流电阻测量值Rx由于双路电桥源幅值不完全相等引入的相对标准不确定度ur1(Rx)为
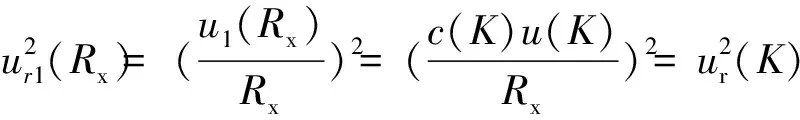
(21)
式中:K——电桥源双路输出的幅值比例。
交流电阻测量值Rx由于双路电桥源相位不完全正交引入的相对不确定度ur2(Rx)为
(22)
式中:Δθ——电桥源的双路波形输出相位差。
5.2 测量不确定度来源分析
1)u(R0)的不确定度来源如下:
a)电桥源的频率分辨力引入的相对标准不确定度ur1(f0);
b)电桥源的频率示值误差引入的相对标准不确定度ur2(f0);
c)标准电容器上级溯源引入的相对标准不确定度ur(C0)。
2)u(Rx)的不确定度来源如下:
a)双路电桥源幅值不完全相等引入的相对标准不确定度ur1(Rx);
b)双路电桥源相位不完全正交引入的相对标准不确定度ur2(Rx);
c)校准装置短期稳定性引入的相对标准不确定度ur3(Rx);
d)装置连接线引入的相对标准不确定度ur4(Rx);
e)实验室环境温湿度变化引入的相对标准不确定度ur5(Rx)。
6 测量不确定度的评定
6.1 交流电阻标准值引入的不确定度u(R0)
1)直角电桥源的频率分辨力引入的相对不确定度ur1(f0)
本文设计的直角电桥源频率分辨力为δ=1×10-6,在此范围内测量值服从均匀分布,按B类评定,其不确定度按式(23)计算
(23)
式中:δ——直角电桥源的频率示值分辨力。
经计算得到
ur1(f0)=2.9×10-7
2)直角电桥源的频率示值误差引入的相对不确定度ur2(f0)
根据测试数据得知,直角电桥源的频率最大允许误差Δf0=6.3×10-7。在此范围内测量值服从均匀分布,按B类评定,其不确定度按式(24)计算
(24)
式中:Δf0——直角电桥源的频率最大允许误差。
经计算得到
ur2(f0)=3.6×10-7
3)计算由直角电桥源频率不准确引入的相对不确定度ur(f0)
直角电桥源不准确引入的相对不确定度ur(f0)按式(25)计算
(25)
经计算得到
ur(f0)=4.6×10-7
4)标准电容证书上的相对不确定度ur(C0)
标准电容器的不确定度主要是上级溯源引入的不确定度。通过查阅标准电容器的上级证书,可以得到标准电容的标准值和测量不确定度为
ur(C0)=2.0×10-6
5)交流电阻标准值引入的相对标准不确定度ur(R0)
根据式(20),经计算得到
ur(R0)=2.0×10-6
6.2 交流电阻测量值引入的标准不确定度u(Rx)
1)直角电桥源双路幅值不完全相等引入的相对不确定度ur1(Rx)
由于数字式直角电桥源的双路正弦电压波形无法做到幅值完全相等,因此幅值的不准确性会引入测量不确定度ur1(Rx)。采用数字多用表8508A进行测试,利用8508A的短期稳定性测量自修正后的幅值。经过测试,直角电桥源双路输出的幅值比例误差K为0.999 995。u(K)应满足
(26)
根据式(22),经计算得到
ur1(Rx)=2.9×10-6
2)直角电桥源双路相位不完全正交引入的相对不确定度ur2(Rx)
由于数字式直角电桥源的双路正弦电压相位无法做到完全正交,因此相位的不正交性会引入测量不确定度ur2(Rx)。经过测试,直角电桥源双路输出90°的相位偏差Δθ为0.002°。u(Δθ)应满足
(27)
根据式(23),经计算得到
ur2(Rx)=3.5×10-7
3)校准装置短期稳定性引入的相对不确定度ur3(Rx)
对测试点频率1.591 55kHz、标准电容100nF、交流电阻1kΩ,在相同条件下短时间重复测量交流电阻值10次,得到10组测量数据,见表2。
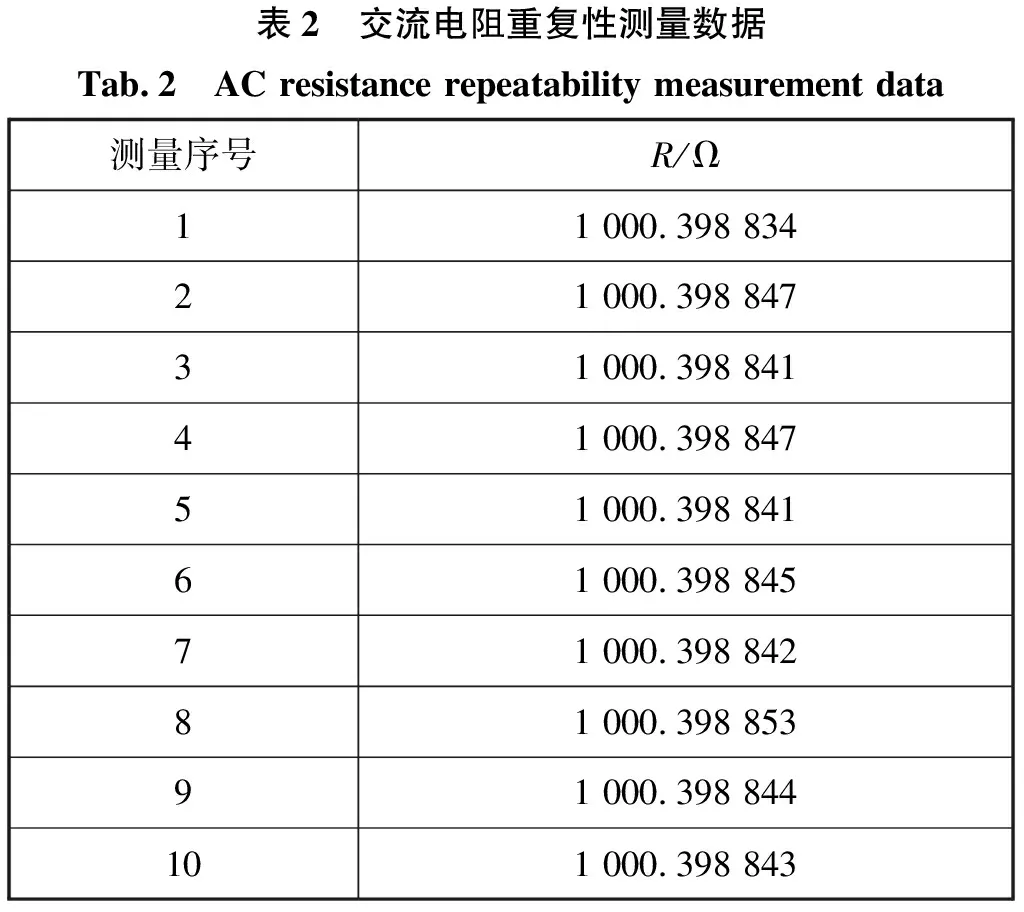
表2 交流电阻重复性测量数据Tab.2 AC resistance repeatability measurement data测量序号R/Ω11 000.398 83421 000.398 84731 000.398 84141 000.398 84751 000.398 84161 000.398 84571 000.398 84281 000.398 85391 000.398 844101 000.398 843
采用贝塞法公式计算测量标准偏差,作为短期稳定性的不确定度分量ur3(Rx)为
(28)
经计算得到
ur3(Rx)=5.0×10-6
4)装置连接线引入的相对不确定度ur4(Rx)
测试设备自身的开路清零和短路清零功能可以有效消除装置连接线的阻抗等杂散分量引入的误差,对测量结果影响较小,因此该项误差可以忽略;
5)实验室环境温湿度变化引入的相对不确定度ur5(Rx)
交流电阻校准装置在实验室恒温恒湿条件下,其环境温度和相对湿度变化导致的量值变化很小,因此该项误差可以忽略。
6)交流电阻测量值引入的相对标准不确定度ur(Rx)
交流电阻测量值引入的不确定度ur(Rx)按式(29)计算
(29)
经计算得到
ur(Rx)=5.9×10-6
交流电阻校准测量装置测量不确定度分量,见表3。
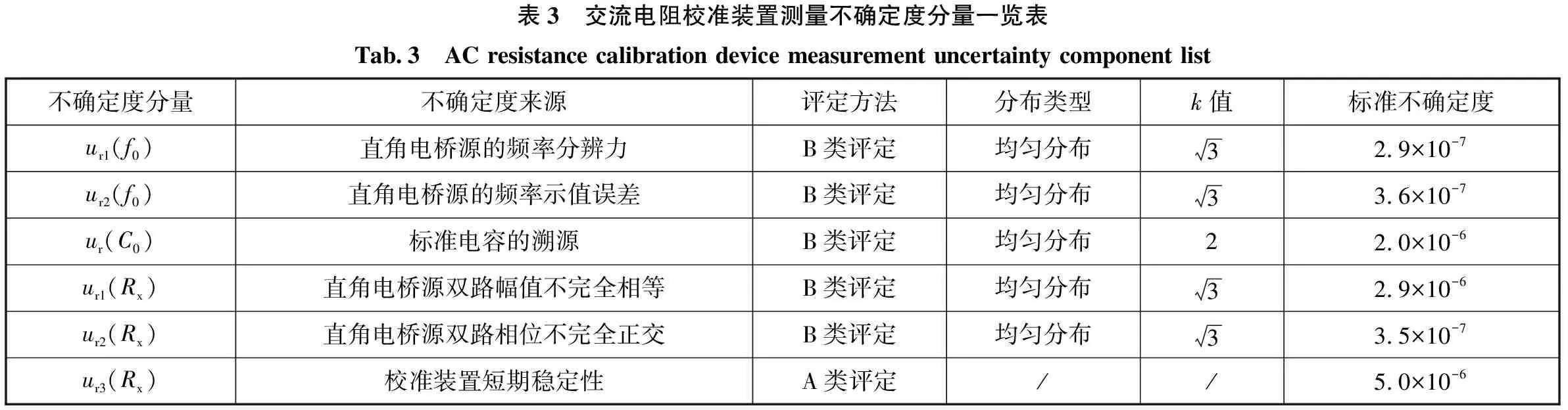
表3 交流电阻校准装置测量不确定度分量一览表Tab.3 AC resistance calibration device measurement uncertainty component list不确定度分量不确定度来源评定方法分布类型k值标准不确定度ur1(f0)直角电桥源的频率分辨力B类评定均匀分布32.9×10-7ur2(f0)直角电桥源的频率示值误差B类评定均匀分布33.6×10-7ur(C0)标准电容的溯源B类评定均匀分布22.0×10-6ur1(Rx)直角电桥源双路幅值不完全相等B类评定均匀分布32.9×10-6ur2(Rx)直角电桥源双路相位不完全正交B类评定均匀分布33.5×10-7ur3(Rx)校准装置短期稳定性A类评定//5.0×10-6
6.3 合成校准不确定度计算
上述交流电阻校准装置的测量不确定度分量彼此互不相关,因此合成标准不确定度ur(Δ)满足[9]
(30)
代入各个测量不确定度分量,得到合成标准不确定度ur(Δ)为
ur(Δ)=6.2×10-6
6.4 扩展不确定度
扩展不确定度按式(31)计算
Ur=kur(Δ)
(31)
取扩展因子k=2,则扩展标准不确定度Ur为
Ur=2ur(Δ)=1.2×10-5(k=2)
7 结束语
本文基于单直角电桥的工作原理,采用数字式直角电桥源作为交流电阻校装置的主要部分,搭建了基于单直角电桥的交流电阻校准装置。当电桥达到平衡时,流经指零仪的电流为零,根据电桥的平衡方程推导得到交流电阻的校准值。通过在不同的频率下选择不同的标准电容,可将交流电阻量值溯源到电容标准上。本文对搭建的交流电阻校准装置进行测试,得到交流电阻的校准数据,并对测量结果进行不确定度分析,得出交流电阻校准装置的最佳测量不确定度可达1.2×10-5(k=2)。通过本文的测试和不确定度分析,对于使用基于单直角电桥原理搭建交流电阻校准装置可与基于其他原理(如双直角电桥法、数字采样法等)建立的交流电阻校准装置所得到数据进行比对,彼此之间互相验证,对于保障交流电阻溯源数据的可靠性具有重要的意义。

