行星变速箱故障模拟试验工况参数确定
冯辅周,吴守军,杨大为
(1.陆军装甲兵学院车辆工程系,北京 100072;2.68302 部队,四川德阳 618408)
0 引言
行星变速箱具有体积小、传递扭矩大、传动比丰富等特点[1],在大型机械传动系统中得到了广泛应用[2]。然而,由于传动系统工作载荷动态变化,导致其齿轮等关键零件经常出现裂纹、断齿等故障,造成严重的安全隐患和经济损失[3]。为了及时准确发现故障并排除,需要研究故障诊断、预测等技术,实现故障的预先发现和处理。故障诊断技术和方法的研究往往需要借助故障模拟试验台采集的振动信号来进行。而故障模拟试验台的系统组成复杂、搭建周期长、成本高、操作难度大[4]。随着计算机技术的发展,涌现出大量仿真软件,在工业领域得到了广泛应用。本文利用三维建模软件ProE 建立了行星变速箱的三维模型,利用ANSYS 建立了行星变速箱箱体的有限元模型,将上述两者模型导入动力学分析软件ADAMS 中建立了齿轮-箱体刚柔耦合模型,利用刚柔耦合模型仿真分析行星变速箱的运转规律和响应特点[5],初步获取了故障模拟实物试验所需的参数,为实物试验台的搭建提供指导。
1 行星变速箱动力学建模
1.1 行星变速箱结构
某型装甲车辆行星变速箱是底盘传动系统的关键构件,它通过改变传动比,可以在较大的范围内改变车辆的牵引力和速度。该行星变速箱通过主离合器和传动箱与发动机连接,通过左右联轴器与左右行星转向器连接。
1.2 动力学建模
依据行星变速箱构造和传动原理,并对变速箱模型进行合理简化,使用ProE 软件建立行星变速箱的三维模型,如图1 所示。

图1 三维模型
齿轮啮合变形对变速箱动力学特性影响较小,在对计算结果要求不高的情况下可以视为刚性体[6],而变速箱箱体是一个小阻尼多自由度的连续弹性体,受力后会产生变形,箱体任意两点的距离发生改变,不能将箱体视为刚性体,必须考虑对箱体进行柔性化而建立柔性体模型[7]。ADMAS 软件本身有限元分析能力较弱,对变速箱箱体这种复杂构件不能直接柔性化,需要借助有限元软件进行分析[8]。使用ANSYS 软件将箱体离散为细小的网格[9],采用截断Lanczos 法计算箱体模态并输出模态中性文件(Modal Neutral File,MNF),将模态中性文件导入ADAMS 软件中,使箱体刚体模型柔性化[10],从而建立箱体柔性体模型如图2 所示。

图2 箱体柔性体模型
刚柔耦合动力学模型由传动部分多刚体模型和箱体柔性体模型两个部分构成,两部分通过轴承耦合。轴承实体模型复杂,仿真分析计算量巨大,为便于动力学建模,常采用轴套力模拟轴承[11]。轴套力相当于一个六分量弹簧结构,通过定义6 个方向的刚度值和阻尼值来模拟轴承刚度和阻尼的影响。通过轴套力将传动部分和箱体耦合,建立的齿轮—箱体刚柔耦合模型如图3 所示。

图3 齿轮—箱体刚柔耦合模型
2 仿真分析
2.1 挡位确定
行星变速箱结构复杂,不同挡位时工作的行星排不一样,确定行星变速箱挡位对故障诊断十分重要。某个挡位下,若故障齿轮所在的行星排不工作,如轮系整体回转或静止不动,此时故障齿轮不承受载荷,则无法提取故障特征。若同时工作的行星排过多,振动信号相互耦合,将增加故障特征提取难度。因此,针对不同齿轮的故障,需要考虑故障模拟试验的挡位设置。各挡位的行星排工作情况见表1。
以K3 行星排齿轮故障为例进行分析,在空挡时K3 行星排不动,在Ⅴ挡时,K3 行星排整体回转,这两个挡位K3行星排齿轮不啮合,不产生故障信号。在其他5 个挡位时,K3 行星排齿轮均啮合产生振动信号,但不同挡位振动信号成分不同,信号处理难度也不同。在Ⅳ挡时,只有K3 行星排工作,K1 和K2 行星排均不承载,可以排除K1 和K2 行星排的干扰,降低振动信号处理难度。其他4 个挡位时,工作的行星排较多,如Ⅲ挡时3 个行星排都承载工作,振动信号成分非常复杂,数据处理更为困难。故针对K3行星排齿轮故障时,应选择Ⅳ挡。
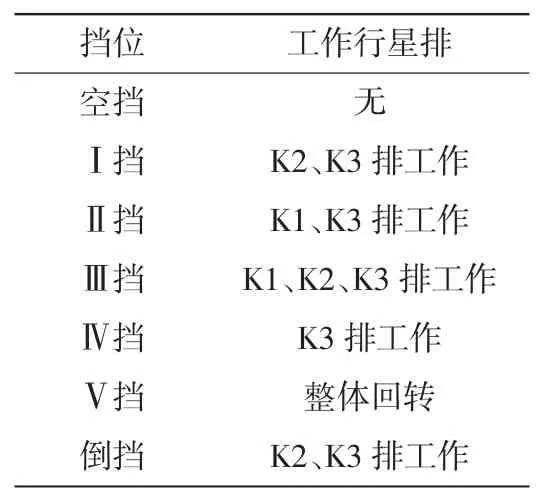
表1 各挡位行星排工作情况
2.2 转速确定
在不同输入转速下,行星轮系振动情况不相同,箱体表面振动信号也会发生变化。故障试验采用变频电动机模拟实车发动机作为驱动,变频电动机转速可调节范围在(0~1500)r/min。动力学分析时设定输入转速分别为:600 r/min、900 r/min、1200 r/min、1500 r/min,得到不同输入转速下箱体表面测点Marker_3 加速度信号。引入峰峰值、均方根值和幅值平均值衡量振动信号能量和强度,时域指标见表2。
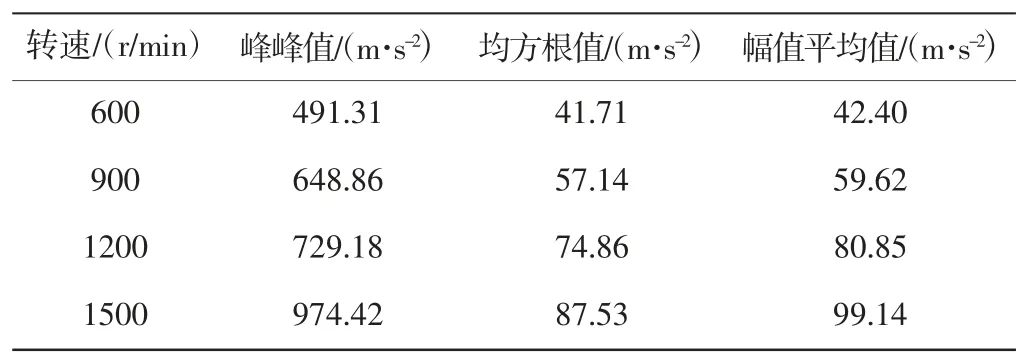
表2 不同转速加速度信号时域指标
分析可知,主动轴输入转速越大,箱体表面测点Marker_3加速度信号峰峰值越大,均方根值越大,幅值平均值越大,测点振动越剧烈。因为行星轮系输入转速越大,单位时间故障齿轮啮合次数越多,因故障产生的冲击次数越多,行星轮系振动越剧烈,箱体振动也更明显。故主动轴输入转速1500 r/min,即驱动电机输入转速为1500 r/min,传感器采集振动信号最强。
2.3 负载确定
在不同负载下,行星轮系振动情况不相同,变速箱箱体表面振动信号也会发生变化。故障试验采用加载发电机模拟实车左右主动轮作为负载,加载发电机扭矩可调节范围在(0~900)N·m。故设定动力学模型中的输出轴负载扭矩分别为0 N·m、300 N·m、600 N·m、900 N·m,得到不同负载下箱体表面测点Marker_3加速度信号,信号时域指标见表3。

表3 不同负载加速度信号时域指标
分析可知,输出轴负载越大,箱体表面测点Marker_3 加速度信号峰峰值越大,均方根越大,幅值平均值越大,测点振动越剧烈。因为行星轮系负载越大,故障齿轮啮合力越大,因故障产生的冲击越大,齿轮轴振动越剧烈,传递至箱体的振动也更剧烈。故输出轴负载扭矩为900 N·m,即加载发电机加载扭矩为900 N·m 时,传感器采集振动信号最强。
2.4 测点确定
对于某型行星变速箱故障诊断系统,振动传感器采集变速箱振动信号,经过一系列信号处理后用于诊断决策。作为变速箱状态信息的载体,合理的传感器配置能全面真实有效反映变速箱运行状态信息,保证故障特征的成功提取。
传感器测点优化应该从两个方面考虑:一方面要考虑工程实际,传感器测点应该具有可操作性,振动传感器安装时要求接触面光洁平整,以保证传感器采集到的振动信号的可靠性,对于安装条件受限的测点应剔除,对于本文研究的变速箱,因其结构复杂,拆装流程繁琐,还应该优先考虑变速箱箱体表面测点,避免频繁拆卸变速箱,便于安装及拆卸传感器,简化测试流程,降低诊断成本。另一方面要考虑传感器测点的有效性,测点应该对故障信息敏感,距离诊断部件尽可能近,可获取更多故障信息。
综合考虑变速箱内部结构和箱体表面传感器安装条件,预先选定5 个测点如图4 所示。其中,测点1 位于右侧定轴轮系上方的箱体上,测点2 位于K2 排齿圈正上方的箱体上,测点3 位于K3 排齿圈正上方的箱体上,测点4 位于箱体左侧端盖上,测点5 在箱体底部正中央。测点1、2、3、5 测试方向均为竖直方向,测点4 测试方向为变速箱轴向。
峭度指标、波形指标、峰值指标、脉冲指标和裕度指标对脉冲冲击比较敏感,当齿轮断齿故障发生时,指标值均有不同程度变化。如果齿轮发生故障,啮合产生脉冲越多,冲击幅值越大,即振动信号越偏离正常状态,指标值一般会相应增大。不同指标敏感度和稳定性不同,同时使用多种指标以保证指标性能,从而更好检验传感器测点的有效性。各测点相应时域指标值见表4。

图4 传感器测点位置示意图
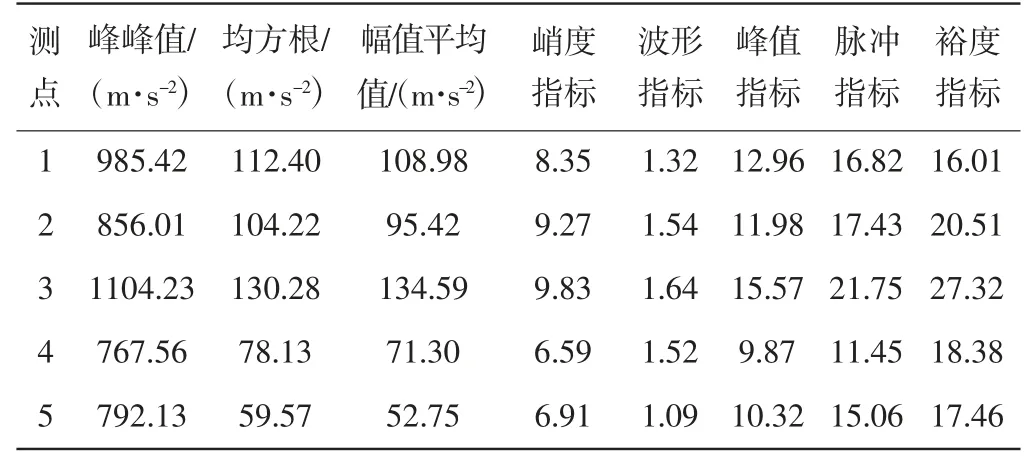
表4 不同测点加速度信号时域指标
由时域波形可知,测点3 振动最剧烈,测点1、2 振动较剧烈,测点4、5 振动较弱。从各项时域指标来看,测点3 各项指标值较大,表明测点3 振动剧烈,信号冲击成分明显,包含故障信息多,对故障最为敏感。测点3 距输出轴轴承座最近,采集到振动信号较强。测点5 位于箱体底部,有较厚的加强筋隔振,采集到振动信号较弱。由频谱可知,测点3 频谱出现了行星轮系啮合频率(529 Hz)及其倍频(1058 Hz、1578 Hz),断齿故障特征频率(17 Hz)及其倍频(34 Hz),定轴齿轮啮合频率(450 Hz)及其倍频(900 Hz、1350 Hz),故障频带最易识别。测点1、2 行星轮系故障频率也较为明显,虽然测点1 振幅略大于测点2,但由于测点1 距主动轴轴承最近,频率成分中定轴齿轮啮合频率更明显。测点4、测点5 频谱主要成分为定轴轮系啮合频率,很难识别行星轮系故障频率。综上,振动传感器测点应以测点3 为主,测点1 和测点2 为辅,排除测点4 和测点5。
3 试验验证
3.1 试验台组成
根据仿真分析结果,搭建行星变速箱故障模拟试验台,试验台主要包括驱动电机、发电机、液压站、转速扭矩仪、振动传感器等,如图5 所示。驱动电机通过传动箱和离合器传递动力至变速箱,变速箱再将动力经增速箱传递至负载发电机。驱动电机为变速箱的驱动,可通过控制平台在(0~1500)r/min 内调节转速。发电机为变速箱的负载,可通过控制平台在(0~900)N·m 内调节加载扭矩。液压站通过输油管道和回油管道为变速箱液压换挡系统和润滑系统提供油液。转速扭矩仪测量输入轴和输出轴的转速和扭矩,振动传感器测量箱体表面振动加速度。
3.2 参数设置

图5 故障模拟试验台
依据行星变速箱和试验台实际情况,试验工况设定:驱动电机转速分别为600 r/min、900 r/min、1200 r/min、1500 r/min;加载发电机加载扭矩分别为空载、900 N·m;行星变速箱挡位分别为Ⅰ挡、Ⅱ挡、Ⅲ挡、Ⅳ挡、Ⅴ挡。齿轮故障设置在K3行星排Z30 太阳轮某轮齿齿面上,切割部分轮齿以模拟断齿故障,如图6 所示。振动传感器测点选择测点1、测点2 和测点3,位置如图7 所示。试验数据分析采用的工况设置情况见表5。

图6 Z30 太阳轮故障

图7 振动传感器测点
3.3 试验信号分析
针对行星轮既自转又公转的复合运动情况,需要考虑行星轮回到初始位置的周期问题,即采集的信号应该包括同一个行星轮回到初始位置的完整周期,这样信号才能对应着行星轮系运行的相同过程,信号之间才有可比性。在行星变速箱挡位Ⅳ挡,输入转速为1500 r/min 时,计算得K3 行星排参数见表6。由表可知,行星轮自转频率为行星架转频的2 倍,说明行星架每转一圈,行星轮自转两圈,与太阳轮啮合15×2=30次,啮合次数与太阳轮齿数相等,说明太阳轮也刚好与行星轮啮合一个周期,此时行星轮旋转到初始位置。行星轮转到初始位置历时t=1/17.65≈0.056 6 s。试验采样频率20 kHz,每次采样30 个周期,间隔30 个周期继续采样。
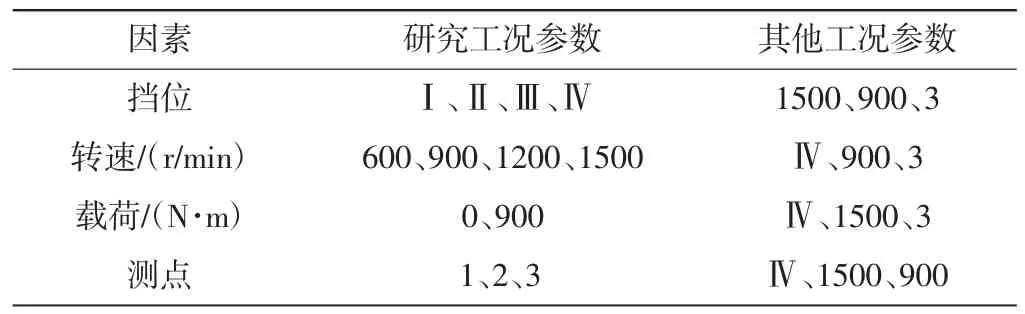
表5 试验工况设置
不同挡位情况下得到的振动信号时域波形和频域波形如图8 所示。由图可知,Ⅳ挡的时域波形幅值最大。可以初步判断选择Ⅳ挡的合理性。不同转速下得到的振动信号时域波形和频域波形如图9 所示。由图可知,1500 r/min 的时域波形幅值明显大于其他转速的幅值,因此选择该转速更有利于故障信号的提取。不同载荷下得到的振动信号时域波形和频域波形如图10 所示。由图可知,900 N·m 的时域波形和频谱的幅值都明显大于空载时的幅值,因此选择该载荷有利于提取故障信息。不同测点的振动信号时域波形和频域波形如图11 所示。由图可知,测点1 的时域波形幅值最大,主要原因是测点1 距离定轴齿轮系较近,所以信号能量较大,针对K3 太阳轮故障,应选择定轴齿轮频率成分少的测点,故选择测点3。

表6 K3 行星排齿轮参数

图8 不同挡位的时域波形和频域波形

图9 不同转速的时域波形和频域波形
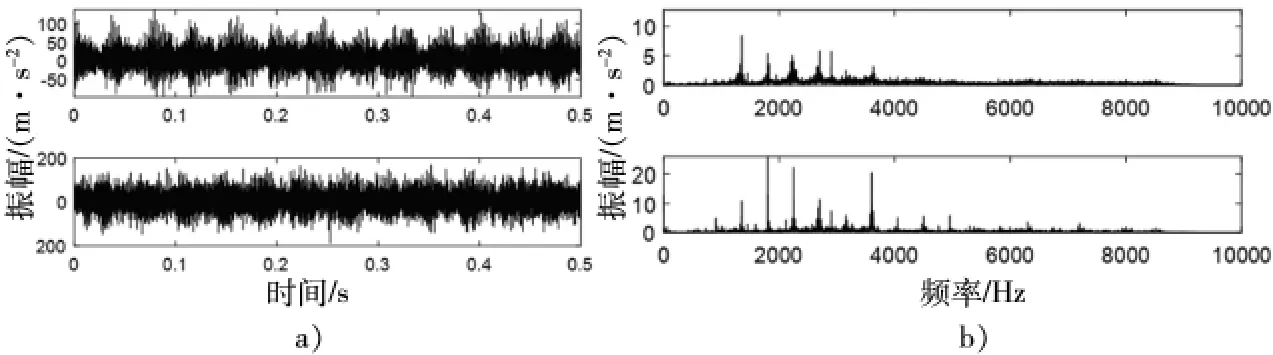
图10 不同载荷的时域波形和频域波形
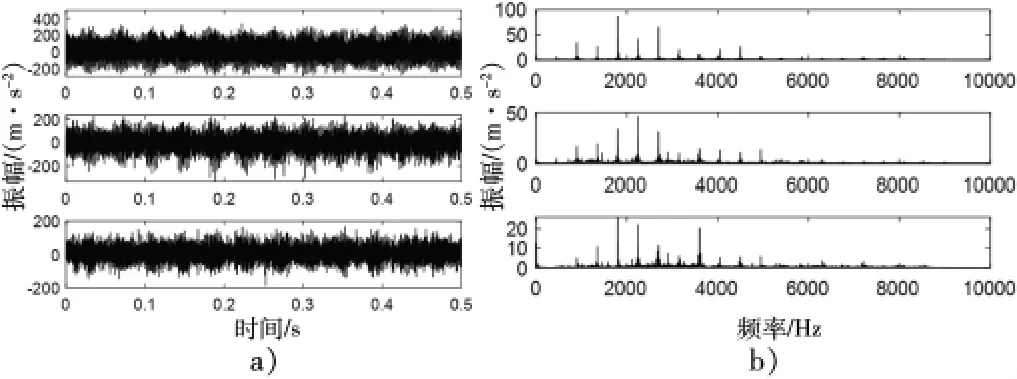
图11 不同测点的时域波形和频域波形
4 结论
综合运用ProE、ANSYS 和ADAMS 仿真软件建立了行星变速箱三维模型、柔性箱体模型和齿轮—箱体刚柔耦合模型,基于动力学模型进行了仿真分析。依据齿轮故障类型和行星排工作情况确定了行星变速箱挡位,即当K3 行星排齿轮故障时选择Ⅳ挡;依据时域指标确定了输入转速为1500 r/min 和载荷为900 N·m,依据测点的可操作性和有效性确定了振动传感器测点位置3 为最优测点。根据仿真得到的工况参数,开展了台架试验,分析了不同挡位、不同转速、不同载荷和不同测点的试验信号的时域波形和频谱图,初步验证了仿真结果的可靠性,为下一步开展故障模拟实物试验提供指导。

