Eあect of stress ratio on HCF and VHCF properties at temperatures of 20°C and 700°C for nickel-based wrought superalloy GH3617M
Aoshuang WAN, Junjiang XIONG
School of Transportation Science and Engineering, Beihang University, Beijing 100083, China
KEYWORDS High cycle fatigue;High-temperature;Nickel-based superalloy;Stress ratio;Very high cycle fatigue
Abstract This paper attempts to investigate the effects of stress ratio and high temperature on the HCF (high-cycle-fatigue) and VHCF (very-high-cycle-fatigue) behaviors of nickel-based wrought superalloy GH3617M. Fatigue tests over the full HCF and VHCF regimes were conducted on superalloy GH3617M subjected to constant-amplitude loading at five stress ratios of -1, -0.5, 0,0.4, and 0.8 in environments of 20°C and 700°C temperatures. From experimental observation and fractographic analysis, fatigue mechanisms were deduced to reveal the synergistic interaction between high temperature and stress ratio on the HCF and VHCF behaviors of superalloy GH3617M. A phenomenological model was crafted from available fatigue design knowledge to evaluate the synergistic interaction, and a good correlation between predictions and experiments has been achieved.
1. Introduction
Due to superior mechanical properties (e.g., excellent strength and stiffness, superior fracture toughness, good resistance to corrosion, oxidation, and creep, etc.), in recent years, singlecrystalline and polycrystalline superalloys have been extensively applied in advanced aero-engines as turbine disc and blade materials to sustain a wide temperature range from 25°C to 1000°C. High temperature has significant influences on the HCF behavior and fatigue mechanism, and there always exists a transition of fatigue mechanism from the low-temperature brittle-cleavage to the high-temperature ductile-quasi-cleavage for some superalloys.1-8Meanwhile,stress ratio also notably influences the HCF behaviors and fatigue mechanism of superalloys.9-13For some low- and highstrength steels as well as titanium alloys,14-16experimental results usually follow a stepwise curve form in fatigue S-N diagram from the HCF to VHCF regime. Conversely, for some single-phase ductile materials,17,18fatigue strength monotonically reduces over the full HCF and VHCF regimes, and no horizontal asymptote appears on fatigue S-N diagram. Crack nucleation always changes from the surface-nucleated mode for the HCF regime into the interior-nucleated mode for the VHCF regime.14-16,19-22High temperature often causes oxide layers and fatigue mechanism transition from the transgranular to intergranular mode, significantly affecting the VHCF behaviors.23In a high-temperature fatigue process, the HCF properties are generally dominated by oxidation-assisted failure,whereas the VHCF behaviors are governed by cyclic plastic localization and accumulation.24Additionally, fatigue mechanism usually changes with an increasing stress ratio,immensely impacting the VHCF behaviors.16,25-27From the above literature, there seems to be a significant body of research dealing with the HCF and VHCF behaviors as well as the effects of high temperature and stress ratio on the HCF and VHCF behaviors.
In practice, some critical parts (e.g., turbine discs and blades)in advanced aero-engines often suffer from substantial oscillating loads with high loading frequencies, high stress ratios, and small stress amplitudes covering the VHCF regime at an elevated temperature. High temperature and high stress ratio can occur simultaneously, and the synergistic interaction between high temperature and high stress ratio is much more severe than each one occurring on its own during crack initiation and growth. Therefore, it is important for engineering design in advanced aero-engines to fully understand the synergistic interaction between high temperature and high stress ratio on the VHCF properties of turbine disc and blade materials. However, the synergistic interaction between high temperature and high stress ratio on the VHCF properties of turbine disc and blade materials has not been investigated yet, which is the focus of this paper.
2. Experiments
2.1. Experimental procedures
All specimens were prepared from nickel-based wrought superalloy GH3617M for fatigue tests. Tables 1 and 2 respectively demonstrate the nominal chemical composition (wt%) and mechanical performances of super-alloy GH3617M, and Fig. 1 illustrates the geometric configuration and dimensions of specimens. All tests were carried out on a QBG-50kN electric servo tester through axial cyclic loading with a sinusoidal waveform,at loading frequencies ranged from 80 to 140 Hz,in the environment of air moisture. It is worth pointing out that the effect of ultrasonic loading frequency on the VHCF behavior has not been fully understood yet.28,29As a result, in this work, fatigue tests were conducted under conventional 80-140 Hz frequencies over the full HCF and VHCF regimes.The stress ratios were-1,-0.5,0,0.4,and 0.8,and the experimental temperatures were 20°C and 700°C, which were controlled through a drum heating apparatus of high-temperature furnaces and a QBT-1200K split. The experimental temperatures fluctuated within ±2°C. It is noteworthy that during fatigue test for each specimen, the stress ratio was constant(i.e., -1 or -0.5, 0, 0.4, 0.8), at a given maximum nominal stress, the nominal stress amplitude was also constant, andthus the fatigue test was termed as a constant-amplitude loading test. Moreover, during fatigue test for each specimen at a given stress ratio, the loading frequency depended on the inherent stiffness of the specimen,which approached to a constant value until final rupture. Since the inherent rigidities for all specimens are close to each other, the loading frequencies for all specimens varied from 80 to 140 Hz. In fact, previous research30-32has revealed that the effect of a loading frequency of less 250 Hz on fatigue life is negligibly small (i.e., less than 3%), so loading frequencies ranged from 80 to 140 Hz are argued to be valid and appropriate for fatigue tests in this work. In addition, in order to investigate the synergistic interaction between high temperature and high stress ratio on the HCF and VHCF properties, the stress-controlled method was applied in fatigue tests for conveniently comparing the HCF and VHCF properties. In the case of a stress ratio of 0.8 and a temperature of 20°C, the maximum stress is higher than the yield limit,but the mean stress is lower than the yield limit, so the stress-controlled method was still used in fatigue tests.

Table 1 Nominal chemical composition of superalloy GH3617M (wt%).

Table 2 Mechanical properties of superalloy GH3617M.
According to the ASTM standards E468-90,33E739-91,34and STP91A,35at least four groups of fatigue tests at different levels of fatigue stress were firstly conducted within fatigue lives ranged from 104to 106cycles. As is well known, fatigue life monotonically increases with a decreasing level of fatigue stress within fatigue lives ranged from 104to 106cycles. As a consequence, at least four groups of fatigue tests were performed to determine a quantitative variation law of fatigue S-N property from 104to 106cycles, by adjusting the level of fatigue stress based on experimental result of prior specimen.33Subsequently, based on fatigue up-and-down procedure,35,36the tests were performed to separately measure fatigue strengths corresponding to fatigue lives of 107, 5×107, and 108cycles.
During fatigue up-and-down tests at each fatigue life, fatigue strength (or level of maximum nominal stress) was firstly estimated, and a test was undertaken at the estimated fatigue strength.If the specimen failed prior to the corresponding fatigue life, the next specimen was then tested at a lower level of fatigue stress.If the specimen did not fail to the corresponding fatigue life, the next test was then carried out at a higher level of fatigue stress. Thereby, each test depended on the experimental result of prior specimen. In this manner and in sequence, fatigue tests continued with a decreasing or increasing level of fatigue stress by using a selected increment of fatigue stress, and then the reverse runout and failed results for fatigue stresses of the un-failed specimen and the prior failed specimen formed a matched pair; at least three matched pairs of fatigue strength were measured for each fatigue life.

Fig. 1 Geometric configuration and dimensions (unit: mm).
If a specimen failed prior to the corresponding fatigue life at the ith level of fatigue stress(or Si),while another specimen did not fail to the corresponding fatigue life at the (i+1)th level of fatigue stress(i.e.,Si+1),then fatigue strength(or maximum nominal stress) pertaining to the corresponding fatigue life was deduced within the range between Si+1and Si. When the difference between Si+1and Si(or Si-Si-1) was small enough and less than 5% of Si+1, fatigue stresses Si+1and Siformed a matched pair, and fatigue strength pertinent to the corresponding fatigue life was the mean value of Si+1and Sias

Obviously, the aforementioned dataset of fatigue stresses Si+1and Siwith the reverse un-failed and failed results formed a randomly sampled individual Sri.Based on the statistics principle, the mean value and standard deviation for fatigue strength pertinent to the corresponding fatigue life were obtained as follows:

where n is the number of matched pairs for fatigue strength.
2.2. Results and discussion
Experimental observations(shown in Fig.2)show that at temperatures of 20°C and 700°C, stress ratio has a significant influence on the failure mode. For four stress ratios of -1,-0.5,0,and 0.4,crack nucleation and growth resulted in final rupture of tested specimens.On the contrary,for a stress ratio of 0.8, plastic necking shrinkage contributed to final ductile rupture, and plastic necking shrinkage increased with an increasing temperature and with an increasing stress ratio.
Experimental results are shown in Fig. 3 and Tables 3 and 4.Fig.3 presents the relationship between the ratio of the maximum strength Smaxto the yield strength σsand the number of stress cycles to fatigue failure N.In Fig.3,the solid points represent experimental data for the surface-nucleated fracture mode, while the hollow points imply that for the interiornucleated fracture mode. Furthermore, the arrows and attendant numbers labeled in the experimental data points denote the number of matched pairs of fatigue strength determined from fatigue up-and-down tests. In Table 3, the stress values represent the maximum nominal stresses. Table 4 shows the transitions for crack nucleation from the surface-nucleated to interior-nucleated mode. From Fig. 3 and Table 4, it can be seen that the cracks for stress ratios ranged from -1 to 0.4 nucleated from the surface-nucleated mode for the HCF regime to the interior-nucleated mode for the VHCF regime,and the transitions appeared at around 1×107cycles, which is also the boundary between the HCF and VHCF regimes.This result is consistent with some previous works,15,22but differs from other works,19-21,29which showed transitions at about 1×106or 2×106cycles.On the other hand,the cracks for a high stress ratio of 0.8 nucleated only in the interiornucleated mode. This consequence has never been reported by previous works. Actually, at a high stress ratio of 0.8, the level of stress amplitude is too low to drive the formation of a surface-nucleated crack, while the mean stress is close to the yield strength, causing severe local plastic deformation inside a specimen to result in interior-nucleated cracks at stress concentration sites.
From the experimental results in Fig.3 and Table 3,the following can be deduced. (i) At temperatures of both 20°C and 700°C, fatigue S-N diagrams for superalloy GH3617M followed stepwise characteristics. Fatigue strength (or maximum nominal stress level) decreased with an increasing number of fatigue stress from 104to 106cycles, followed by a plateau at the classical fatigue endurance limit pertaining to the vicinity of 107cycles, and further decreased in the VHCF regime ranged from 107to 108cycles. This result is consistent with the result in literature.14-16(ii) At temperatures of both 20°C and 700°C, the fatigue strength increased with an increase in the stress ratio. This is probably because fatigue damage (or fatigue life) fundamentally depends on the nominal stress amplitude, and the nominal stress amplitude pertaining to the same fatigue life increases with an increase in the stress ratio. (iii) At the same stress ratio, fatigue strengths are lower at 700°C than at 20°C. One reason for this is that high temperature can increase cyclic local plastic deformation, the PSB (persistent slip band) formation, and micro-pore coalescence, and changes the phase composition of crystals and dislocation-structures,1,2,4ultimately decreasing fatigue life.Moreover, high-temperature creep also occurs in hightemperature fatigue tests, apparently reducing fatigue strength.37,38

Fig. 2 Fatigue experiment pictures.

Fig. 3 Fatigue experimental results.
In order to make a comparison between the fatigue strengths at 20°C and 700°C pertinent to a given fatigue life N, a reduction factor γ is introduced for defining the nondimensional fatigue strength as

where S1N( )and S2N( )are the fatigue strengths pertinent to a given fatigue life N at 20°C and 700°C, respectively.In reality, with an increase in the stress ratio, the cracks commonly open to a greater extent to conduce more and severer oxidation layers at the crack tip arising from cyclic tensile loads, apparently increasing crack growth.

Table 3 Experiments of fatigue strength Smax (unit: MPa).

Table 4 Fatigue life pertaining to the transition from the surface-nucleated to interior-nucleated mode (unit: cycles).
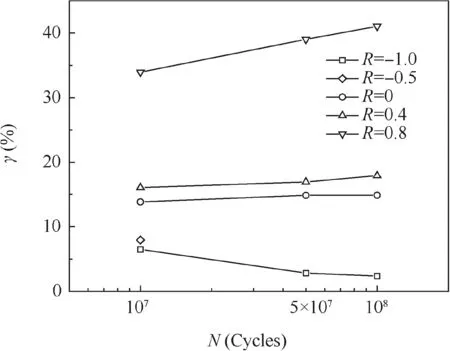
Fig. 4 Reduction factor curves of the fatigue strength.
Owing to the random nature of fatigue damage,a statistical analysis necessitates a great deal of experimental datasets with a large sample size to deduce the population law at high reliability levels. However, the formidable long test time for aforementioned loading frequencies ranged from 80 to 140 Hz limits the number of specimens in the VHCF tests.If more specimens are adopted in tests,more accurate experimental results of fatigue strengths could be determined.
3. Fractographic analysis
From Eq. (4) and the experimental results in Table 3 and Fig. 3, reduction factor curves are obtained (shown in Fig. 4). From Fig. 4, it is clear that at a given fatigue life, if the stress ratio is greater, then the reduction factor γ is also greater. Meanwhile, with an increasing fatigue life, the reduction factor γ increases at a positive stress ratio, but decreases at a negative stress ratio, and nearly maintains constant at a stress ratio of 0. These imply that the adverse effects of high temperature on HCF and VHCF properties increase with an increasing stress ratio, substantially reducing fatigue strength.

Fig. 5 Fractographic pictures in the HCF regime at T=20°C.
In order to demonstrate fatigue mechanism of superalloy GH3617M, representative fracture surfaces of tested specimens were analyzed for providing direct evidences of crack nucleation and growth in unobservable regions on specimens during fatigue tests, by using a scanning electron microscope(shown in Figs. 5-7). In Fig. 5(a) and (a), the red borderlines and the attendant numbers denote the magnified regions,magnification times, and the numbers of corresponding magnified figures.From Figs.5 and 6,fatigue mechanisms from the HCF to VHCF regime could be deduced as follows. (i) The stress ratio had a significant effect on the crack-nucleate mode.Crack formation at a stress ratio ranged from-1 to 0.4 transformed from the surface-nucleated mode in the HCF regime to the interior-nucleated mode in the VHCF regime,and the transition for the nucleated mode appeared at around 1×107cycles, which was also the boundary between the HCF and VHCF regimes(see Fig.5(a), (d),and 6(a) and Table 4).Nevertheless,crack formation at a high stress ratio of 0.8 nucleated only in the interior-nucleated mode. Alternatively, a crack nucleated from the PSBs at the inclusions inside the specimens in the HCF regime (see Fig. 5(h)), but from the growth and aggregation of micro-pores in the VHCF regime (see Fig. 6(e)). Actually, at a low or negative stress ratio in the HCF regime, the PSBs on the specimen surfaces can contribute to the nucleation of a 45° surface crack and then a growth perpendicular to the stress axis until final rupture.21Conversely,in the VHCF regime, the fatigue stress is too low to form the PSBs,and fails to drive the surface crack through adjacent grains,and thus the crack tends to nucleate at the initial microflaws (e.g., microstructural inhomogeneities, micro-pores,inclusions,etc.)inside the specimens resulted from local plastic deformation, where there is a local stress concentration.19(ii)The stress ratio also affected the crack growth mechanism.Fracture surfaces at stress ratios ranged from -1, to 0.4 demonstrated clear origins of fatigue cracks, stable crack growth, and coarse zone of rupture (see Fig. 5(a), (d), and 6(a)). Fatigue cracks grew outward from crack origins in the cleavage-like mode to induce the appearance of river-like patterns and cleavage steps on the crack growth zone (see Fig. 5(e)). Furthermore, with an increasing stress ratio, the cracks opened more significantly for a longer time to lead to more and greater dimples on fracture surfaces owing to local plastic formation, rather than significant fatigue striations (see Fig. 5(b)and(e)).Hence,fracture surfaces were coarser(see Fig.5(c)and (f)). Unlike fracture surfaces at stress ratios ranged from-1 to 0.4,fracture surfaces at a high stress ratio of 0.8 showed an insignificant evidence of crack growth (see Fig. 5(g) and 6(d)).Owing to the severe local plastic deformation arising from the high mean stress and the low stress amplitude, fatigue cracks instantaneously grew outward to cause substantial shear dimples, equal-axis dimples, and cavities until final rupture. Fracture surfaces exhibited a transgranular appearance in the HCF regime (see Fig. 5(h) and (i)), but a mixed transgranular and intergranular appearance in the VHCF regime(see Fig.6(f)).The reason for this is that due to the low stress amplitude, severe local plastic deformation at the crack tip also caused a brittle intergranular appearance on fracture surfaces in the VHCF regime.

Fig. 6 Fractographic pictures in the VHCF regime at T=20°C.

Fig. 7 Fractographic pictures in the HCF regime at T=700°C, R= -1, Smax=350 MPa, N=6.75×104 cycles.
From Figs. 7 and 8, significant effects of high temperature on fatigue properties could be summarized as follows. (i) The oxidation due to high temperature had an influence on crack initiation and propagation.Only a single fatigue origin mostly appeared on fracture surfaces of failed specimens at 20°C.Nevertheless,multiple fatigue cracks occurred from the oxidation sites at 700°C (see Fig. 7(a)). This owes to the brittleness of the oxidation layer arising from high temperature, immensely increasing crack nucleation and growth.Moreover,oxidation layers also emerged on the crack propagation zone to cause black spots covering fatigue striations (see Fig. 8(c)).However, it is hard to find an evidence of oxidation layers on the rupture zone of a fracture surface. Therefore, rupture zones were found to be full with a great deal of equal-axis dimples (see Fig. 7(c)). The reason for this is that in the instant rupture stage, rapid propagation of a crack made inadequate oxidation (due to too short oxidation time) on the rupture zone. (ii) The ductility improvement resulted from high temperature also affected crack propagation. Larger cleavage facets occurred on fracture surface at 700°C than at 20°C(see Figs. 7(a), 8(a), and (b)), which indicates that with an increasing temperature, the inflexion of the crack growth path decreased, and the crack growth rate increased. As a result of the ductility improvement,clearer fatigue striations and larger dimples also appeared on fracture surfaces at 700°C than at 20°C(see Fig.5(b),(c),(b),and(c)).Again,due to the oxidation resulted from high temperature, more secondary cracks emerged on fracture surfaces at 700°C than at 20°C (see Fig. 7(b) and (c)). (iii) High temperature also reduced grainboundary cohesion strength and increased grain boundary slips. A local intergranular appearance was found on the fracture surfaces of tested specimens at 700°C(see Fig.8(b)).This consequence is in a close agreement with the research conclusion in previous literature.23

Fig. 8 Fractographic pictures in the VHCF regime at T=700°C, R=-1, Smax=320 MPa, N=7.30×107 cycles.
It is worth pointing out that the above results from fractographic analysis qualitatively provide an insight into the synergistic interaction between high temperature and high stress ratio on fatigue mechanism of superalloy GH3617M over the full HCF and VHCF regimes, and constitute a fundamental basis for the development of a theoretical model for depicting the aforementioned synergistic interaction.In order to develop a theoretical model for evaluating the aforementioned synergistic interaction on the HCF and VHCF behaviors, further works probably necessitate to quantitatively determine the microstructural sizes of a material (including grains and grain slip boundary, dimple, short crack, oxidation layer, etc.) and the ductility improvement at different stress ratios in hightemperature environments.
4. Model for evaluating effects of the stress ratio and temperature on VHCF properties
Fatigue S - N behavior is one of the most important material properties for depicting crack nucleation under constantamplitude loading. A number of empirical functions (e.g.,exponential or power function models with two, three, and four parameters) have been devised and used in engineering design. Nevertheless, an exponential or power function with two parameters is suitable only for depicting a linear (or stable) fatigue life regime. By considering the effect of fatigue endurance limit,a power function model with three parameters was presented for depicting linear (or stable) fatigue life and long-life regimes, which had a better precision in fitting data than those with two parameters. A power model with four parameters necessitates a large amount of experimental dataset to estimate four unknown parameters by best fitting, even though it covers over the full range of fatigue life, and has the best fitting accuracy. Accordingly, fatigue S-N property depicted by the Basquin's model in a power function with three parameters is commonly implemented to depict material's fatigue behaviors under symmetrically cyclic loading with a stress ratio of -1 as follows:

where S-1represents the fatigue strength (or maximum nominal stress) pertinent to symmetrically cyclic loading. S∞denotes the fatigue endurance limit pertaining to symmetrically cyclic loading. m and C represent the material's constants. N denotes the fatigue life.
Fatigue strength S-1pertinent to symmetrically cyclic loading in the Basquin's model (or Eq. (5)) is a variable with respect to fatigue life. In other words, fatigue strength S-1is different for different fatigue lives. However, fatigue tests are commonly carried out at a specific stress ratio R to determine material's fatigue S-N property.As a result,fatigue stress corresponding to the specific stress ratio R in tests needs to be corrected into the fatigue strength S-1pertinent to symmetrically cyclic loading through a constant-life diagram, and material's fatigue S-N property can then be obtained from Eq. (5). The model parameters S∞, m, and C in Eq. (5) are the material's constants,which can be determined by best fitting from experimental results.
In reality,some constant-life diagrams(e.g.,the Goodman,the Soderberg (or the Smith), the Bagci, and the Gerber models, etc.) have been proposed to correct fatigue stress or strength. Nevertheless, it has been understood from reexamining previous models39that the Soderberg formula is almost conservative for all materials, whereas the Bagci equation is nearly optimistic for all materials.Meanwhile,the Gerber model is valid for ductile materials, however, the nonlinearity formulation limits its use. The Goodman function is conservative for ductile materials and superalloy materials,40although the model is suitable for brittle materials.In general,the empirical Goodman function is employed for correcting the fatigue S-N property as follows:

where Sadenotes the nominal stress amplitude, Smrepresents the mean nominal stress, and σbis the material' ultimate strength.
By means of Eq. (6), it can be shown that

Substituting Eq. (7) into Eq. (5) results in

Eq. (8) depicts a fatigue Sa- Sm- N property surface in a three-dimensional coordinate system. Notably, it can be seen from Table 2 that there exists a certain change in mechanical properties(including the ultimate strength σb)with an increasing temperature. The change in mechanical properties with temperature T trends to be approximately linear, and a linear function is valid for describing the change in the ultimate strength σbwith the temperature T.5,12For this reason, from the experiments of the ultimate strength (shown in Table 2),it is possible to obtain a linear function as follows:

Again, as mentioned above, fatigue endurance limit S∞inevitably and monotonically decreases with an increasing temperature. Therefore, a monotonically-decreasing function is introduced to consider the influence of temperature on fatigue endurance limit, namely,

where α and β are the undetermined constants, andis the fatigue endurance limit at 0°C.
Substituting Eqs. (9) and (10) into Eq. (8), one has

Eq. (11) depicts the relationship between fatigue stress amplitude Sa, mean stress Sm, fatigue life N, and temperature T, and is termed as the fatigue Sa- Sm- N - T surface model.The unknown constants m, C,, α, and β in Eq. (11)can be determined by best fitting from experimental data.
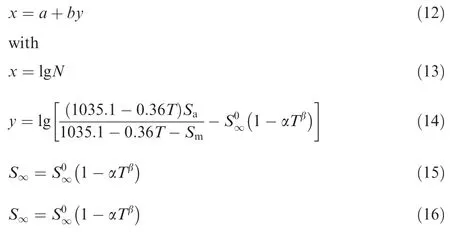
Taking the logarithm form of Eq. (11) yields Apparently, the logarithm form (or Eq. (12)) is linear, so the linear regression principle is used to estimate the undetermined parameters a and b as well as the linearly-dependent coefficient r (i.e., the Pearson coefficient) as follows:

where
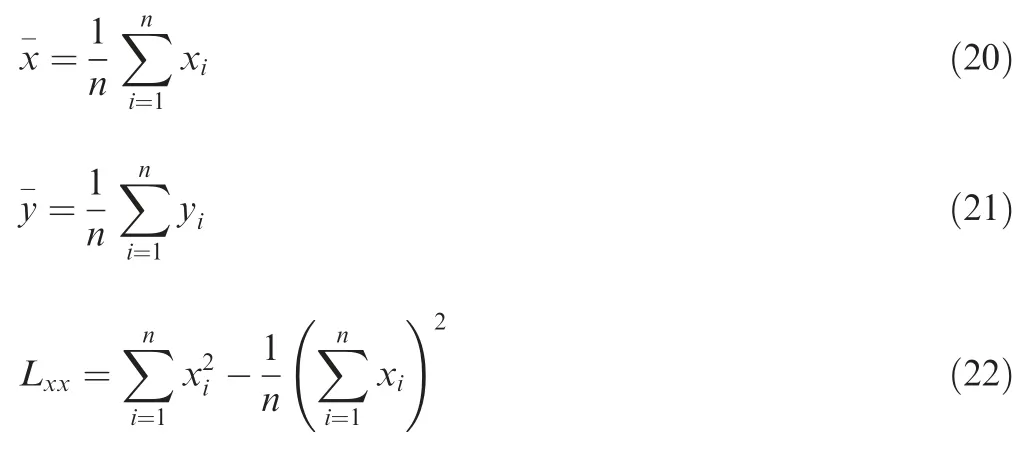

From the above equations, it can be seen that, Lyy, and Lyxare associated with the undetermined constants, α,and β.Alternatively,,Lyy,and Lyxare functions with respect to, α, and β. Therefore, the undetermined parameters a, b,and r are also functions with regard to, α, and β. By best fitting or by optimizing the absolute value of the linearlydependent coefficient, it is possible to have solving equations with regard to S0∞, α, and β. Then, the unknown constants m and C are determined as

Apparently, Eq. (11) is a phenomenological surface model crafted from available fatigue design knowledge for depicting the effects of stress ratio and temperature on fatigue S - N property.In comparison with conventional methods(i.e.,comparing fatigue S - N properties at different stress ratios and temperatures),this formulation is more effective and expedient to evaluate the variation of fatigue S - N property with changes in the stress ratio and temperature. Alternatively,Eq. (11) is suitable for evaluating fatigue S - N properties at any stress ratio and any temperature.


Fig. 9 Fatigue Sa - Sm - N surfaces deduced from Sa - Sm - N - T model.

Table 5 Comparison between predicted and experimental fatigue strengths Smax (unit: MPa).

The correlation coefficient and standard deviation are respectively 0.93 and 11.74 in best fitting of fatigue Sa- Sm- N - T surface. Fatigue S - N properties for superalloy GH3617M are deduced from fatigue Sa- Sm- N - T surfaces (or Eq. (27)). Fatigue Sa- Sm- N surfaces for superalloy GH3617M at 20°C and 700°C determined from Eq. (27) are drawn in Fig. 9, while fatigue S - N curves are plotted in Fig. 3. From Eq. (27) and Fig. 9, it is clear that for a given fatigue life of 107cycles, two fatigue Sa- Sm- N surfaces for the HCF and VHCF regimes can degenerate to an identical Goodman constant-life curve (or Eq. (6)), and the Goodman constant-life curve corresponding to 107cycles is the intersection line between two fatigue Sa- Sm- N surfaces for the HCF and VHCF regimes.
Comparisons between the predictions of fatigue strengths determined from Eq. (27) and the experiments (listed in Table 3)are shown in Table 5.From Table 5,it can be deduced that the predictions from fatigue Sa- Sm- N - T surfaces are mostly in good agreement with those from the experiments.The most relative deviations of predictions from fatigue Sa- Sm- N - T surfaces from experiments are less than 20%,and only few are greater than 20%, but less than 40%. One reason for the deviation of the model results from the experimental data is the small sample size of the test data. It is well known that fatigue lives are often very scattered.If more specimens are used for fatigue tests at each stress ratio and each mined, and more accurate calculated results can be obtained.
From Figs. 3 and 8, it is apparent that fatigue Sa- Sm- N surface is lower at 700°C than at 20°C, that is, elevated temperature has an adverse influence on the HCF and VHCF properties of superalloy GH3617M. Moreover, fatigue life on fatigue Sa- Sm- N surfaces decreases with an increase in the level of fatigue stress, and the difference between fatigue Sa- Sm- N surfaces at 700°C and at 20°C also reduces with an increase in the level of fatigue stress. Therefore, we argue that Eq.(11)has adequately and logically depicted the physical natures and the quantitative variation laws of fatigue behaviors with changes in the stress ratio and temperature over the full HCF and VHCF regimes.Importantly,this surface model is more effective and expedient for evaluating the synergistic interaction between high temperature and high stress ratio on the HCF and VHCF properties in contrast to the conventional method of comparing fatigue S - N properties at different stress ratios and temperatures.
5. Conclusions
This paper seeks to investigate the synergistic interaction between high temperature and high stress ratio on the HCF and VHCF properties of superalloy GH3617M and to craft a technique for evaluating the aforementioned synergistic interaction. Particular novel features are six-fold:
i. Fatigue S - N diagrams for superalloy GH3617M over the full HCF and VHCF regimes followed stepwise characteristics.Fatigue strength decreased with an increasing number of fatigue stress from 104to 106cycles,followed by a plateau at the classical fatigue endurance limit pertaining to the vicinity of 107cycles,and further decreased in the VHCF regime ranged from 107to 108cycles.This result agrees with that in literature.14-16Fatigue strength increased with an increase in the stress ratio, but decreased with an increasing temperature. The adverse effect of high temperature on the HCF and VHCF properties increased with an increasing stress ratio.
ii. Stress ratio had a significant influence on fatigue mechanism for superalloy GH3617M.For four stress ratios of-1,-0.5,0,and 0.4,crack nucleation and growth caused fatigue failure.On the contrary,for a stress ratio of 0.8,plastic necking shrinkage contributed to final ductile rupture, and plastic necking shrinkage increased with an increasing temperature and with an increasing stress ratio.
iii. Stress ratio has an effect on the crack nucleation mode.For stress ratios ranged from-1 to 0.4,crack nucleation changed from the surface-nucleated mode in the HCF regime into the interior-nucleated mode in the VHCF regime, and the transition of crack nucleation appeared at around 1×107cycles, which is also the boundary between the HCF and VHCF regimes.This result is consistent with some previous works,15,22but differs from other works.19-21,29However, for a high stress ratio of 0.8, only the interior-nucleated mode occurred over the full HCF and VHCF regimes. This consequence has never been reported by previous works.
iv. Stress ratio also affected the crack growth mode. For stress ratios ranged from -1 to 0.4, fatigue cracks grew outward from crack origins in the cleavage-like mode,and fracture surfaces became coarser with an increasing stress ratio. Nevertheless, for a high stress ratio of 0.8,fatigue cracks instantaneously grew outward to cause substantial shear dimples, equal-axis dimples, and cavities until final rupture, and fracture surfaces exhibited a transgranular appearance in the HCF regime, but a mixed transgranular and intergranular appearance in the VHCF regime.
v. High temperature had an adverse effect on the HCF and VHCF properties of superalloy GH3617M.Only a single fatigue origin mostly appeared on fracture surfaces of failed specimens at 20°C. Conversely, multiple fatigue cracks occurred from oxidation sites and a local intergranular appearance was found on fracture surfaces of tested specimens at 700°C; in addition, larger cleavage facets occurred on fracture surfaces at 700°C than at 20°C.
vi. A fatigue Sa- Sm- N - T surface model was crafted to depict the change of fatigue behaviors with the stress ratio and temperature from the HCF to VHCF regime.In contrast to the conventional method of comparing fatigue S - N properties at different stress ratios and temperatures, the proposed model is more expedient and has an acceptable precision for evaluating the synergistic interaction between high temperature and high stress ratio on the HCF and VHCF properties.
Acknowledgement
This project was supported by the National Natural Science Foundation of China (No. 51875021).
 CHINESE JOURNAL OF AERONAUTICS2019年9期
CHINESE JOURNAL OF AERONAUTICS2019年9期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Fast Track
—— New Column Launched by CJA - Investigation on the interface damage in drilling low-stiあness CFRP/Ti stacks
- Sealing reliability modeling of aviation seal based on interval uncertainty method and multidimensional response surface
- A linear ADRC-based robust high-dynamic doubleloop servo system for aircraft electro-mechanical actuators
- Cardinality compensation method based on information-weighted consensus filter using data clustering for multi-target tracking
- Area-oriented coordinated trajectory planning of dual-arm space robot for capturing a tumbling target
