差分信息熵的网络时序型隐蔽信道检测*

张宇飞,沈 瑶,杨 威,肖䶮汉,黄刘生

1(中国科学技术大学 苏州研究院,江苏 苏州 215123)

2(中国科学技术大学 软件学院,江苏 苏州 215123)

3(中国科学技术大学 计算机科学与技术学院,安徽 合肥 230026)

通讯作者:张宇飞,E-mail:SA614137@mail.ustc.edu.cn

网络隐蔽信道技术是指利用网络中的合法通信信道构建秘密信道,进行隐秘信息的传输.隐蔽信道在加密传输信息内容的同时,对传输信息行为也进行了加密.传统的加密技术很容易引起注意,并被加以破解.随着密码学等相关理论的发展,密文的破译技术得到了飞速发展,加密技术的可靠性将面临挑战.隐蔽信道技术相比加密技术具有更强的隐蔽性.自1973 年Lampson 提出隐蔽信道的概念至今,对于隐蔽信道技术的研究成果层出不穷；与此同时,隐蔽信道检测技术也随着隐蔽信道技术的发展而被研究.对于隐蔽信道领域的正向研究,主要目标是提出具有更高信道容量、更高传输效率、更强隐蔽性的隐蔽信道实现方案,以保障重要信息传输过程的安全；反向研究则是探索更通用、更可靠、检测率更高的隐蔽信道检测算法,及时发现并阻止不法分子利用隐蔽信道窃取机密信息.

根据存储载体的不同,现有的网络隐蔽信道实现方式主要分为两类:网络存储型隐蔽信道利用网络数据包中的某些字段编码隐秘信息进行传输；网络时序型隐蔽信道则将隐秘信息编码到相邻数据包的时间间隔中,利用网络中数据包的传输速率、发送时间和到达时间进行隐秘信息的传输.

时序型隐蔽信道利用数据包的时间间隔传输信息,而数据包的时间间隔容易受到网络环境影响.当网络环境不稳定时,数据包的时间间隔也会发生较大的抖动,造成隐蔽信道传输信息的错误.因此相比存储型隐蔽信道,时序型隐蔽信道的可靠性较差.但是时序型隐蔽信道的优点在于其隐蔽性很强,实现机理和信息编码过程的复杂多变,使得目前尚无方法有效检测所有类型的网络时序型隐蔽信道；并且随着网络和通信技术的发展,网络环境也在逐步改善,这也使得时序型隐蔽信道的准确率和可靠性在逐步提升.因此,时序型隐蔽信道检测技术的研究成为了目前隐蔽信道检测技术研究工作的重点.

针对上述问题,本文提出一种基于差分运算和信息熵的网络时序型隐蔽信道检测算法,其主要贡献如下:

(1)提出了差分信息熵(difference entropy)的概念,通过理论研究得到差分熵的特性,为检测算法的有效性提供理论基础；

(2)提出了基于差分信息熵的时序型隐蔽信道检测算法,并通过一系列实验确定算法的最优参数设定；

(3)设计了对照实验,比较了本文提出的差分熵算法和相似度算法、随机性检测算法、CCE 算法以及熵评估算法对于IPCTC,TRCTC,JitterBug 这3 种时序型隐蔽信道的检测效果,着重研究了对于JitterBug隐蔽信道的检测效果.

本文第1 节介绍研究背景,简要描述本文中涉及到的一些预备知识.第2 节提出差分信息熵的概念并描述其特性.第3 节介绍基于差分信息熵的网络时序型隐蔽信道检测算法的原理.第4 节介绍算法的实现过程,包括数据的收集、处理方式以及算法在程序实现过程中涉及到的参数设定.第5 节通过设计实验来检验算法的性能和效果.最后,第6 节说明目前研究过程中存在的问题以及之后的研究方向,并且总结全文.

1 预备知识

1.1 隐蔽信道

隐蔽信道的概念最初由Lampson 在1973 年提出,他将隐蔽信道定义为本意不是用来传输信息的通信信道[1].即:如果采用某种手段或方法,利用一个本不是用于通信的系统或过程来传输信息,那么这种手段或方法就构建了一条隐蔽信道.文献[1]中,作者将两个具有调用关系的程序称为 Customer 和 Service,并给出了在Customer 调用Service 时,程序Service 可能将Customer 的信息泄露给第三方的6 种可能的情况,进而表明:即使Customer 在调用Service 时为Service 规定了严格的数据访问权限,Customer 的数据依然有可能被泄漏.通过对6 种情况的阐述,作者认为,Service 程序将产生3 种类型的通信信道.

· 存储信道:Service 可以将数据存储在可以被第三方访问到的存储空间中来实现数据的隐秘传输；

· 加密信道:Service 利用某种方式,在合法信道中嵌入机密信息进行传输；

· 隐蔽信道:通过某种方式,利用本不是用来传输信息的过程或机制来传输信息.

Lampson 隐蔽信道的定义后来被Tsai 等人进一步完善.Tsai 给出的隐蔽信道的定义是:给定一个强制安全策略模型M以及其在操作系统中的解释I(M),I(M)中的两个主体I(Sh)和I(Sl)之间的通信是隐蔽的,当且仅当模型M中的对应主体Sh和Sl之间的任何通信都是非法的[2].该定义认为:隐蔽信道只与系统的强制访问控制策略模型相关,并且广泛存在于部署了强制访问控制机制的安全操作系统、安全网络和安全数据库中[3].

从1973 年至今,对于隐蔽信道方面的研究成果层出不穷.Wang 等人、Zander 等人对于目前已有隐蔽信道方面的研究成果进行了充分的总结和归纳[3,4].Wang 在其综述中描述了4 种类型的隐蔽信道[3].

(1)数据库信道:利用数据库系统对外传输数据,主要利用数据库中的存储资源、管理资源以及事务并发控制机制构建隐蔽信道；

(2)阈下信道:基于公钥密码技术的数字签名、认证等应用密码体制的输出密码数据中建立起来的一种隐蔽信道；

(3)网络信道:网络信道可以分为两种:第1 种存在于多级安全系统中,是一种用于从高安全级向低安全级传输信息的隐蔽信道；第2 种则不涉及多级安全的概念,在普通的通信信道中嵌入一层隐蔽的通信信道,这里普通信道是隐蔽信道的载体；

(4)推理信道:严格意义上讲,推理信道并不是一种通信信道,它利用某种方式,通过对公开数据的查看来推理出隐私数据的内容.这种技术通常用于获取数据库中的私有信息,例如:利用数据库中的某些聚集查询和函数查询来推断某一条数据记录的具体内容.

从文献[3]可以看出,对于隐蔽信道的研究已经扩展了Lampson 和Tsai 最初对于隐蔽信道的定义.Lampson提出的3 类信道,在现今的研究中都可以归于隐蔽信道的范畴；Wang 所描述的4 类隐蔽信道中,数据库信道对应于 Lampson 描述的存储信道,阈下信道和网络信道则对应于 Lampson 提出的加密信道,推理信道对应于Lampson 的隐蔽信道.目前研究的隐蔽信道主要针对利用网络协议规定的数据帧或数据报来构建的隐蔽信道,对应于Wang 在其综述中提到的第2 类网络信道.

1.2 网络隐蔽信道

网络隐蔽信道是指利用计算机网络中的各种协议,以合法通信信道作为载体,构建用于传输隐秘信息的通信信道.这里关于术语隐蔽信道(covert channel)的意义和指代的范畴,Zander 在其综述中做出了明确的界定[4]:利用网络中的各种协议帧的格式来嵌入隐秘信息的技术称为隐蔽信道；通过加密技术将隐秘信息嵌入到数据明文中的方式则称为隐写术(steganography)；术语信息隐藏(information hiding)涵盖了以上两者.作为载体的合法信道则称为公开信道(overt channel).

对于网络隐蔽信道技术,我们可以从多个角度进行分类.

(1)按照隐秘信息编码原理划分,网络隐蔽信道可以划分为网络存储型隐蔽信道和网络时序型隐蔽信道:前者主要利用网络协议中的一些控制字段编码隐秘信息,实现隐秘传输；后者则利用了数据包的发送时间、接收时间、时间间隔来进行隐秘信息的编码；

(2)按照传输载体划分,网络隐蔽信道可以分为网络协议隐蔽信道和网络应用隐蔽信道:前者利用的是涉及到网络基础建设的底层协议,诸如TCP,UDP,IP,ICMP 以及其他的链路层协议；后者利用的则是涉及到高级网络应用的应用层协议,诸如HTTP,HTTPS,SMTP 以及SSH 等；

(3)按照与合法信道的关系划分,网络隐蔽信道可以分为主动式隐蔽信道和被动式隐蔽信道.主动式隐蔽信道的发送方和接受方与合法信道的发送方和接收方是相同的,因此,主动式隐蔽信道可以直接操纵信道的容量和传输速率；被动式隐蔽信道的发送方、接受方与合法信道的发送方、接收方不同,而是介于合法信道发送方和接收方之间.被动式隐蔽信道仅仅是借助于合法信道作为载体,对于信道的控制力较弱,隐蔽信道的传输能力和性能也主要取决于作为载体的合法信道的情况.被动式隐蔽信道和主动式隐蔽信道的区别可以用图1、图2 来描述.

Fig.2 Active covert channel图2 主动式隐蔽信道

以上的分类方式中,第1 种分类方式最能体现隐蔽信道的本质,下文中的讨论都基于该分类方式.

1.2.1 网络存储型隐蔽信道

网络存储隐蔽信道主要利用网络协议帧中的字段编码隐秘信息,构建隐蔽通信信道.常用的载体有IP 数据报中的服务类型(TOS)[5]、标志位(flag)[6]、数据报编号(identification)[7,8]、生存时间(TTL)[9,10]、数据报长度等字段以及TCP 报文中的紧急指针(URG)[11]、报文序号(sequence)[12,13]等字段.另外,以上协议中的选项部分和填充字节也可以作为隐秘信息的载体.

网络存储型隐蔽信道的构建不仅可以利用底层的网络协议,还可以利用一些应用层的协议,如HTTP[14-16]和DNS[17]协议.一些TCP/IP 层之下的协议,诸如以太网、令牌环网络中涉及的相关协议也可以作为网络存储型隐蔽信道的载体[18-20].

本文提出的检测算法主要针对网络时序型隐蔽信道,因此对于存储型隐蔽信道,这里仅简要说明.

1.2.2 网络时序型隐蔽信道

网络时序型隐蔽信道将隐秘信息编码为数据包传输过程中的时间间隔,达到隐秘传输的目的.对于主动式的网络时序型隐蔽信道,发送端在发送数据包时就将隐秘信息编码到了数据包的时间间隔中,发送端发送数据包时,发送的时间间隔就根据要传输的隐秘信息进行了调制；对于被动式时序型隐蔽信道,则主要通过拦截、抓取正常网络信道中正在传输的数据包,根据要传送的隐秘信息,将数据包的时间间隔延长或缩短,达到传输隐秘信息的目的.

以下是部分网络时序型隐蔽信道类型的简要介绍.

· IPCTC (IP covert timing channel)

2004 年,Cabuk 提出了一种时序型隐蔽信道称为IPCTC[21],在其实现中,发送方和接受方需要事先约定一个时间间隔t.发送开始后,对于每一个时间间隔t,如果发送方需要发送比特1,就在该时间间隔内发送一个数据包；否则,发送方保持静默,接收方观察数据包到达的时间间隔,就可以得到信道中包含的隐秘信息.如果在时间间隔t之内收到了发送方发送的数据包,传输的数据被识别为比特1；否则,识别为比特0.IPCTC 的传输原理如图3所示.

Cabuk 还在文中给出了发送方和接收方的同步机制,并指出了4 种可能影响IPCTC 隐蔽信道传输性能的因素.其中,时间间隔t直接决定了信道的容量和传输效率:t值越小,信道的传输速率越高；但是时间间隔的减小,会导致传输过程中的错误率提高.理论上,该信道的极限传输速率等同于发送端处理数据的速率.

IPCTC 利用在约定的时间区间中是否发送数据包来表示传输比特0 或比特1.该信道并不是直接将信息编码到数据包时间间隔的数值中,而是利用在时间区间内的发送或不发送数据包的事件,在发送方和接收方之间建立了一个可以共享的布尔值,接收方通过观察这个布尔值的结果来接收隐秘信息.在Zander 的综述中,IPCTC又被称为ON/OFF 隐蔽信道[4].

Fig.3 IP covert timing channel (IPCTC)图3 IPCTC 网络时序型隐蔽信道

· TRCTC (time replay covert timing channel)

2006 年,Cabuk 对其提出的IPCTC 隐蔽信道进行了改进[22],提出了一种新的时序型隐蔽信道——TRCTC.随意确定的时间间隔t很有可能会改变包间隔数据的统计特征,从而使得IPCTC 的隐蔽性和抗检测性降低.TRCTC 首先对正常网络信道中的数据包时间间隔进行采样,然后将采样得到的数据划分为两个集合S0和S1,传输数据时,如果需要传输比特0,就从集合S0中选择一个时间间隔,发送数据包；如果需要传输比特1,就从S1中选择一个时间间隔,发送数据包.由于通信中用到的时间间隔采样自合法通信中的时间间隔,TRCTC 和正常通信产生的包间隔具有相似的数值特性.相比IPCTC,TRCTC 的隐蔽性更好.

· JitterBug

2006 年,Shah 等人提出一种利用用户敲击键盘的时间间隔来编码信息的时序型隐蔽信道——JitterBug[23].JitterBug 设定了一个时间参数ω,如果需要传输比特1,就增加用户两次敲击键盘的时间间隔,使该间隔可以被参数ω整除；如果要传输比特0,就增加时间间隔使其可以被ω/2 整除,但不能被ω整除.显然,参数ω的选择直接决定了信道的容量和传输效率:ω的值越小,信道的传输速率越高；并且,ω的值越小,产生的时间间隔数据和合法信道的数据的相似度就会越高,信道的隐蔽性就越强.Jitterbug 信道的缺点在于它是一个被动式隐蔽信道,不论ω的取值为多少,信道的极限容量和传输效率本质上取决于载体信道的容量和传输效率.

以上3 种方式为时序型隐蔽信道的主要实现方式,除此之外,时序型隐蔽信道的种类还有MBCTC[24],DM[25]等.下文中的研究主要涉及到了上面提到的3 种类型的隐蔽信道,因此对于其他的类型,这里不再赘述.

相比存储型隐蔽信道,时序型隐蔽信道隐蔽性更强,检测时序型隐蔽信道的难度也更大.时序型隐蔽信道是一种即时通信,发送方发送数据后,接收方必须及时接收,否则,数据包传输完毕后,传输的信息也随之丢失.另外,时序型隐蔽信道利用数据包时间间隔进行隐秘信息的编码,所以对于网络环境有一定的要求,当前网络环境的稳定性直接影响到时序型隐蔽信道传输过程的可靠性和传输信息的正确性.

1.2.3 其他类型的网络隐蔽信道

近几年来,对于网络隐蔽信道技术的研究提出了更多的网络隐蔽信道实现方案.存储型和时序型的分类已经无法完全涵盖所有的隐蔽信道类型,例如:利用虚拟机之间共享的硬件资源在两个虚拟机实例之间构建隐蔽信道[26]；利用数据包的排序方式来构建隐蔽信道[27]；利用多条通信流的构建隐蔽信道[28]等.这些隐蔽信道无法从严格意义上讲其属于存储型或时序型的类型,也不在本文的研究范围.

1.3 网络时序型隐蔽信道的检测技术

时序型隐蔽信道将隐秘信息编码到网络数据包传输的时间间隔中.对于合法信道,数据包的时间间隔仅取决于当前的网络环境；而对于时序型隐蔽信道,数据包的时间间隔则主要取决于要传输的隐秘信息.因此,时序型隐蔽信道的包时间间隔数据会在一些统计特征上呈现出和合法信道的差别.所以目前比较成熟的时序型隐蔽信道检测技术主要通过评估待测数据的统计特征,包括均值、方差等统计量,来达到检测和识别时序型隐蔽信道的目的.

Cabuk 认为:由于正常数据包的传输时间间隔仅仅由网络环境决定,因此时间间隔数据的随机性较高；而时序隐蔽信道中的时间间隔用于传输隐秘信息而被刻意操纵,因此随机性比较低[21].基于这样的观点,Cabuk 提出了两种时序型隐蔽信道检测方式.

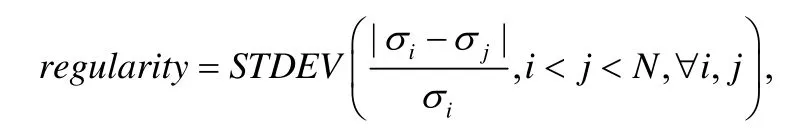
· 第1 种方式称为随机性检测算法,该算法检测数据包时间间隔的标准差.通过将待检测数据划分N个窗口,分别计算每个窗口的标准差,结果分别记为:σ1,σ2,...,σN.然后计算不同窗口标准差的差距的标准差,如下:其中,STDEV表示计算标准差.Cabuk 认为:合法信道数据的随机性高,因此数据的标准差不是恒定的,因此regularity的值也因标准差数据的波动较大；而隐蔽信道数据的随机性低,在传输数据的过程中,包时间间隔的标准差是恒定的,所以regularity的值会很小；

· Cabuk 提出的第2 种检测方式称为ε相似度(ε-similarity),基本思想是:合法通信中的各个数据包时间间隔是相互独立的；而隐蔽信道的数据包间隔编码了隐秘信息,因此数据包时间间隔之间是否独立取决于要传输的数据.ε相似度算法计算排序后的相邻包间隔数据之间的相似度.对于排序后的包间隔数据序列P1,P2,...,PN,相邻数据包间相似度的计算方式如下:

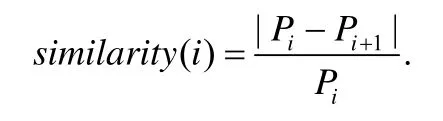
计算所有数据对的相似度后,统计相似度小于ε值的数据的比例.比例越大,待测信道中存在隐蔽信道的可能性就越高.

检测时序型隐蔽信道的另一种较为成熟的技术是评估待测数据的熵率.熵(entropy)是随机变量随机程度的定量度量,它的定义来自于Shannon 提出的信息论[29],而熵率(entropy rate)则是随机变量序列的平均信息熵,或者等价定义为无限个随机变量序列的极限条件熵.熵(记作EN)和熵率(记作ER)的计算方式如下:

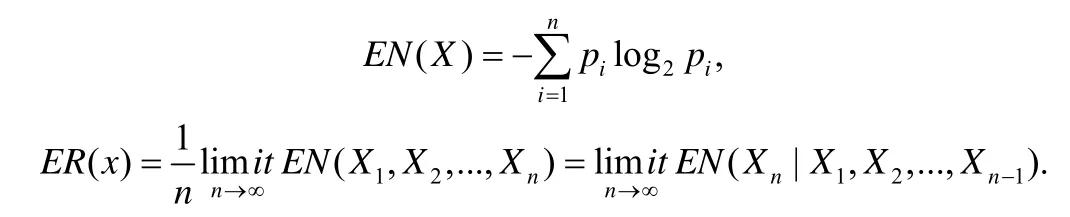
由于熵率是一个极限定义,对于有限的数据无法计算.Gianvecchio 提出一种带修正值的条件信息熵(correct condition entropy),使得可以通过有限的数据来估计熵率[30].计算方式如下:

其中,Xn表示长度为n的随机变量的序列,CE(X1,X2,...,Xn)表示X1,X2,...,Xn的条件信息熵,perc(Xn)则表示测试数据中所有唯一的n长度序列占所有n长度序列的比例,EN(X1)就是随机变量X的熵值.而熵率的估计值就是取不同的n值得到的CCE(Xn)的最小值.

Gianvecchio 的观点和Cabuk 是相同的,同样认为隐蔽信道的数据的随机性要比正常数据低,熵率值越小,信道中含有隐蔽信道的可能性就越高.

检测时序型隐蔽信道还有其他的算法,诸如基于SVM 的隐蔽信道分类器[31-33]、基于神经网络[34-36]的检测算法、基于熵率和标准差的检测方法[37]等.本文提出的检测算法主要基于ε相似度和熵,因此对于其他类型的检测算法,这里不再详述.

2 差分信息熵

本节主要对差分信息熵理论进行阐述.通过下文中的理论分析可以看到,差分信息熵可以同时对待检测数据的分布特性和数值特性进行评估.下文中为了便于分析,首先给出了一些定义和定理,然后对差分信息熵理论进行说明.

2.1 分布特性与数值特性

信息熵是一种对随机变量随机性程度的定量度量.熵的概念源于热力学,由Shannon 在1948 年提出信息论后引入计算机和通信领域[29].离散型随机变量信息熵的计算方式前文中已经给出.Gianvecchio 通过评估数据的熵率来检测时序型隐蔽信道.文献[30]作者用4 种隐蔽信道组织实验验证其提出的CCE 算法的有效性[30]:IPCTC,TRCTC,MBCTC,Jitterbug.根据作者提供的实验数据,CCE 算法对于JitterBug 隐蔽信道的检测效果很差,这主要是因为Jitterbug 隐蔽信道对于数据包间隔做出的修改很小,使得产生的包间隔数据和正常数据在统计特性上的差别很小.

我们认为,利用熵率来对数据进行评估仅仅考虑到了数据的统计特性,而没有考虑数据的数值特性.例如,对于两个离散型随机变量X,Y,假设X可能的取值为1,3,5,7,取到每个值的概率为1/4；Y可能取值是1,5,6,11,取到每一个值的概率同样为1/4.那么代入信息熵计算公式,X和Y得到的熵值是相同的:

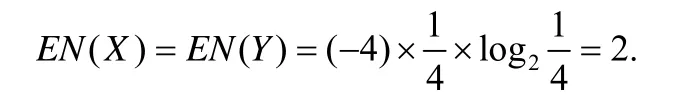
但是很显然,从数值上来看,变量X的规律性更强.对于相互独立的随机变量序列,熵率的值跟熵值是相同的；对于非独立的随机变量序列,熵率的大小低于熵值,此时,熵率和熵值的差距取决于序列中各个元素关联度的大小.Gianvecchio 提出的CCE 算法之所以对于JitterBug 隐蔽信道的检测效果不好,我们认为,主要是因为熵率仅仅评估了待测数据的分布特性,而没有评估待测数据数值特性.根据构建原理,JitterBug 中的时间序列的要么是参数ω的倍数,要么是ω/2 的倍数.因此,Jitterbug 中的任意两个数据的差值一定是一个ω/2 的倍数.就数值特性而言,JitterBug 隐蔽信道中的数据表现出了和正常数据不同的特性.

为了同时对数据的分布特性和数值特性进行评估,我们结合Cabuk 提出的ε相似度算法和Gianvecchio 提出的CCE 算法,提出差分信息熵的概念,进而提出差分信息熵的网络时序型隐蔽信道检测算法.

2.2 离散型随机变量的拆分与合并

为了便于下文中对于差分信息熵的详细说明,首先需要说明下面的定理:

定理1.对于任意的正数序列p1,p2,...,pn,可以得到:

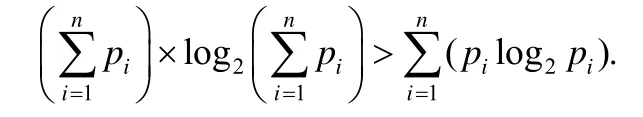
证明:只要将不等式两边的式子求差即可:

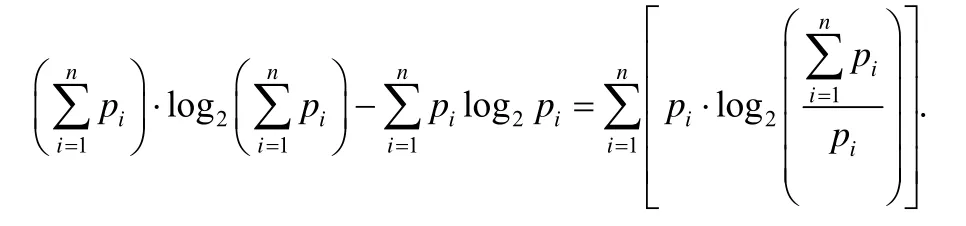
由于序列中的每个pi都是正数,因此,一定是大于1 的数,所以结果和式中的每一项都是正数,也就说明上面的做差结果是大于0 的,原式成立.

对于一个可能的取值有v1,v2,...,vn、对应的概率分别是p1,p2,...,pn的离散型随机变量X,我们可以为其定义两种操作:

定义1.通过随机变量X定义随机变量Y,Y的取值规则如下:

此时,我们可以说随机变量Y由随机变量X通过合并(merge)操作得到.

定义2.定义二值的随机变量a,a以概率q取值为1,以概率(1-q)取值为0,然后通过随机变量X和a定义一个随机变量Z,Z的取值规则如下:

其中,∀1≤i≤n,vn+1≠vi.此时,我们可以说随机变量Z由随机变量X通过拆分(split)操作得到.

现在考虑通过合并和拆分X得到的随机变量Y和Z的熵值.随机变量X具有n个可能取值,而随机变量Y在X的值为vn-1或vn时,取值都是vn,因此Y只有n-1 种可能的取值；而通过拆分操作得到随机变量Z 在X的值为vn时根据随机变量a的取值情况有两种取值:vn和vn+1,因此,Z共有n+1 种可能的取值.通过代入熵计算公式,Y和Z的熵值分别为

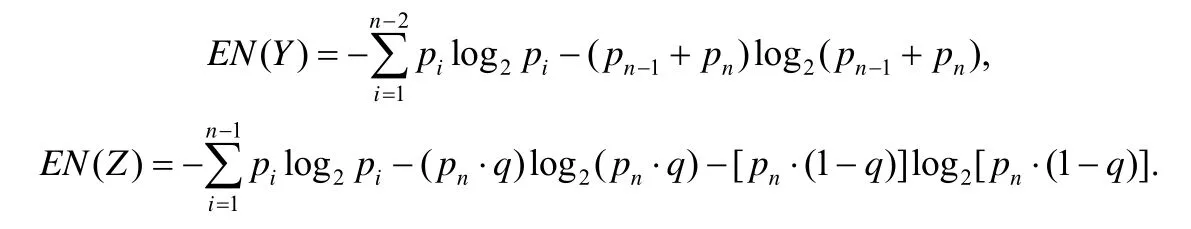
然后,将其和X的熵值做差:

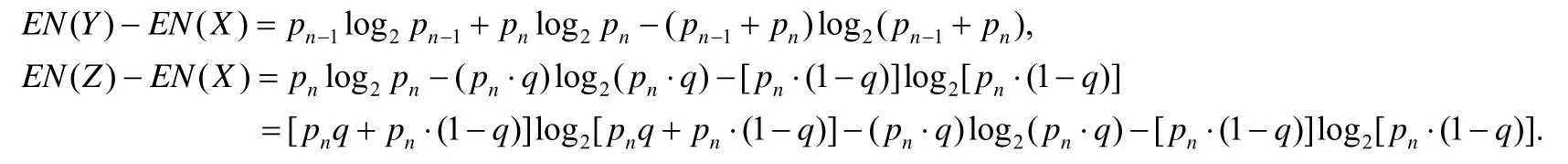
根据定理1,我们可以得到EN(Y)-EN(X)的结果小于0,EN(Z)-EN(X)的结果大于0,因此可以得到如下定理:

定理2.拆分一个随机变量会使熵增大,合并一个随机变量会使熵减小.

2.3 差分值矩阵与差分概率矩阵

本节定义两个辅助矩阵来帮助下文中对于差分信息熵的讨论.

定义3.设离散型随机变量X可能取值有v1,v2,...,vn,对应的概率分别是p1,p2,...,pn,这里为了便于分析,将数值v1,v2,...,vn递增排序.然后定义一个随机变量Y=X1-X2,其中,X1和X2相互独立并且和X具有完全相同的概率分布.此时可以定义一个n×n的矩阵Dv,矩阵中的元素vij表示X1取值vi并且X2取值vj时的Y值；同时还可以定义另一个n×n的矩阵Dp,矩阵中的第i行第j列元素pij表示表示X1取vi、X2取vj时的联合概率.此时称矩阵Dv为变量X的差分值矩阵(difference value matrix),矩阵Dp为变量X的差分概率矩阵(difference probability matrix).

由于X1,X2独立,所以pij就是pi和pj的乘积.X的差分值矩阵和差分概率矩阵如下:

通过观察可以发现,差分值矩阵Dv具有如下的性质.

(1)主对角线上的值均为X1,X2取相同值的情况,因此主对角线上的元素v1,1,v2,2,...,vn,n的值均为0；

(2)关于主对角线互相对称的两个元素的结果互为相反数.显然,对于任意元素vi,j=vi-vj,它关于主对角线的对称位置为vj,i=vj-vi,和vi,j互为相反数；

(3)每一个元素一定都比它上方和右方的元素大.这个结果是显而易见的.任意一个元素vi,j=vi-vj,它右边的元素是vi,j+1=vi-vj+1,上边的元素是vi-1,j=vi-1-vj,由于vj+1＞vj,vi＞vi-1,所以vi,j＞vi-1,j；同时,vi,j＞vi,j+1；

(4)矩阵中数值最大的元素在左下角,最小的则在右上角；并且任意一行、任意一列中一定不存在相同的元素；

(5)整个矩阵中最多包含n2-n+1 个不同的值,最少包含2n-1 个不同的值.对于前者,由于整个矩阵包含n2个元素,而主对角线上的元素都是0,共有n个0,如果其余的元素任意两个都不相同,那么此时,矩阵包含的不同元素最多,这个最大值就是n2-n+1；对于后者,则基于这样的事实:不论X具有怎样的数值特征,矩阵Dv中,总可以找到一条从左下角的最大元素到达右上角的最小元素的路径,使得沿着该条路径移动时,方向总是向上或向右,此时这条路径一定包含2n-1 个元素.图4 给出了对于X有4 个不同取值的情况,沿着路径遍历这些元素时,得到的一定是严格递减的序列.也就是说,不论X具有怎样的数值特征,在矩阵中都可以找到2n-1 个不同的元素.

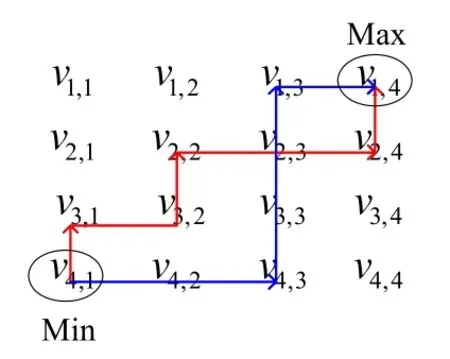
Fig.4 There are at least 2n-1 different elements in the matrix Dv (two paths are shown in this figure)图4 Dv 矩阵中至少包含2n-1 个不同元素(图中给出了其中的2 条路径)

2.4 差分信息熵及其特征

2.4.1 差分信息熵的定义

对于离散型的随机变量X,我们用下面的方式定义其差分信息熵:

定义4.对于一个离散型随机变量X,定义一个随机变量Y=X1-X2,其中,X1和X2相互独立并且和X具有完全相同的概率分布.此时,随机变量X的差分信息熵为随机变量Y的信息熵,记作DEN(X),即:

下面说明差分信息熵DEN(X)的特征.根据上文中差分矩阵的性质(5),对于有n个可能取值的随机变量X做差分运算后,最多有n2-n+1 种不同的结果；最少有2n-1 种不同结果.而如果不考虑差值,仅仅考虑X1,X2不同的取值组合,则有n2种情况.我们可以将这些不同的取值组合按照差分值Y分组,得到的分组数目记为C,并将这C个分组分别为g1,g2,...,gC.图5 是一个分组的样例.

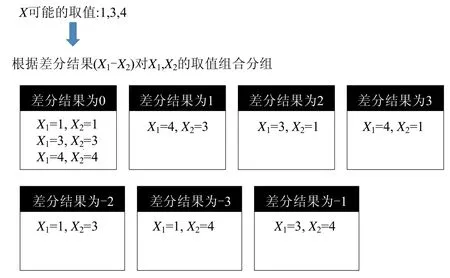
Fig.5 Example of classifying the combination of X1and X2according to the difference result (X1-X2)图5 根据差分结果对随机变量的取值组合分组的样例

显然,这里的分组数目C满足下面的关系式:

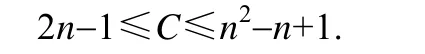
分组完成后,可以得到计算差分熵DEN(X)的公式如下:

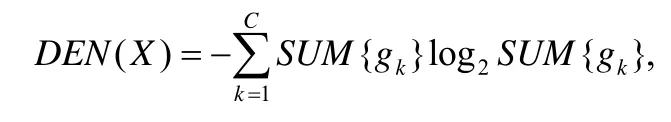
其中,

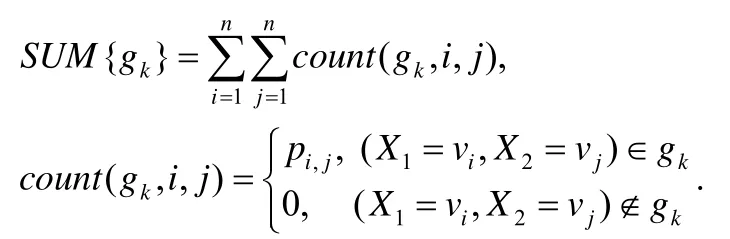
2.4.2 数值特性对差分熵的影响

本节说明数值特性对于差分熵的影响,并给出差分熵的值域.下文将分3 种情况说明:首先考虑两种特殊情况,然后再说明更一般的情况.

情况1.取值序列v1,v2,...,vn是等差数列,假设公差为d,此时,差分值矩阵变成了如图6 所示的形式.

Fig.6 Difference value matrix in the case 1图6 情况1 的差分值矩阵

如图6 所示,此时位于同一条斜线上的元素的值都相等,矩阵中不同的值的个数恰好为最小值2n-1,即C=2n-1,此时对应的差分熵为

关于这个值和熵值EN(X)的大小关系,我们尚未找出完全的证明方式,这里仅仅给出一个不完全的分析.根据差分概率矩阵Dp,我们可以定义一个离散随机变量X′,X′共有n个可能的取值,记作:r1,r2,...,rn,而对应的概率,则由下面的规则给出:

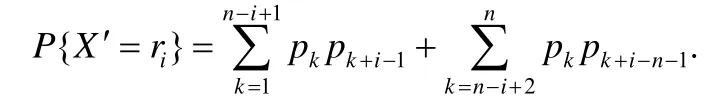
X′的分布律可以用图7 来描述.

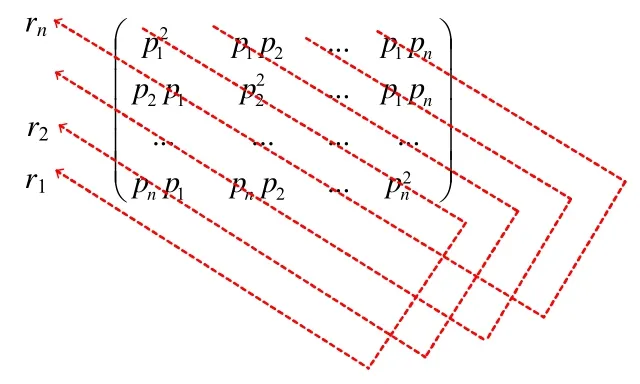
Fig.7 Distribution law of random variable X′图7 随机变量X′的分布律

为了更直观地表达,我们列举各个变量值对应的概率如下:

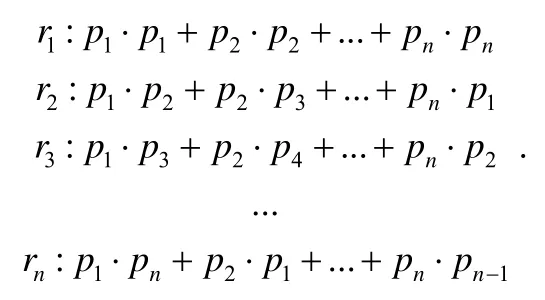
可以看到,X′的每个概率值都是由X的概率值通过轮换相乘然后求和得到.这是一个平均化的运算过程,这意味着X′的概率分布比X跟接近于均匀分布(此处尚未找到完全的证明方式,但多次实验结果表明该结论是正确的).由于均匀分布的随机性最高,熵值最大,所以可以得到下面的结论:

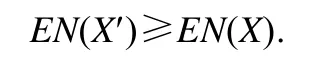
下面通过拆分的方式,通过X′构造Y,将上文中每个ri概率值拆分出来,如图8 所示.

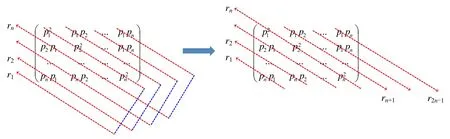
Fig.8 Getting Y from X′ by splitting operation图8 拆分X′得到Y

可以看到,此时Y的熵值就是DENmin(X).根据定理2,拆分使得熵值增大,因此:

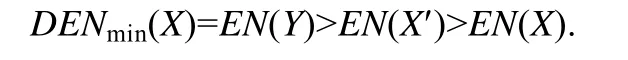
表1 是通过程序模拟得到的实验数据,对于每一个不同的分布律,表中只列出各个取值的概率,随机变量具体可以取到哪些值并不影响实验结果,因此没有列出.实验数据充分表明,前文中的结论在绝大多数情况下是正确的.

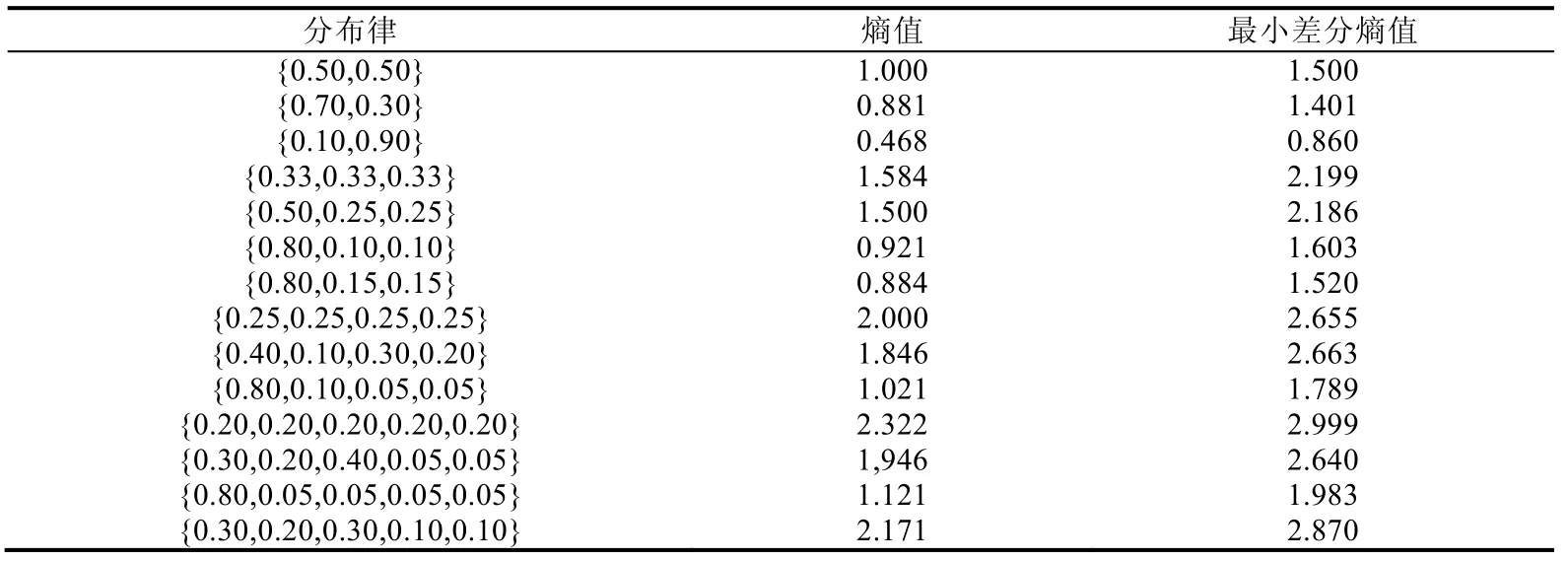
Table 1 Data from the experiment comparing values of entropy and minimum difference entropy表1 随机变量熵值和最小差分熵值的比较实验数据

情况2.取值序列v1,v2,...,vn呈不规则分布,使得任意两个不同的项作差值结果都不相同,此时,差分结果Y可能的取值个数为最大值n2-n+1,因此C=n2-n+1.此时,对应的差分熵值是:

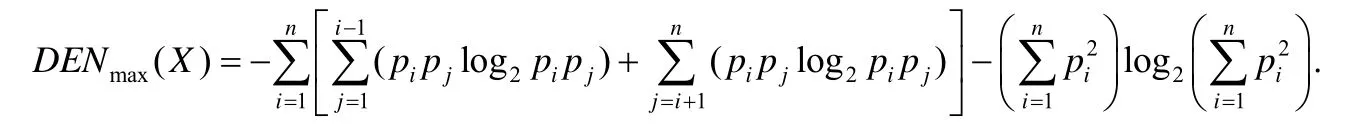
根据定理1,可得:

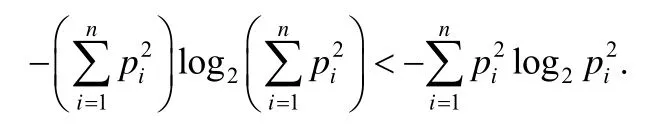
于是,

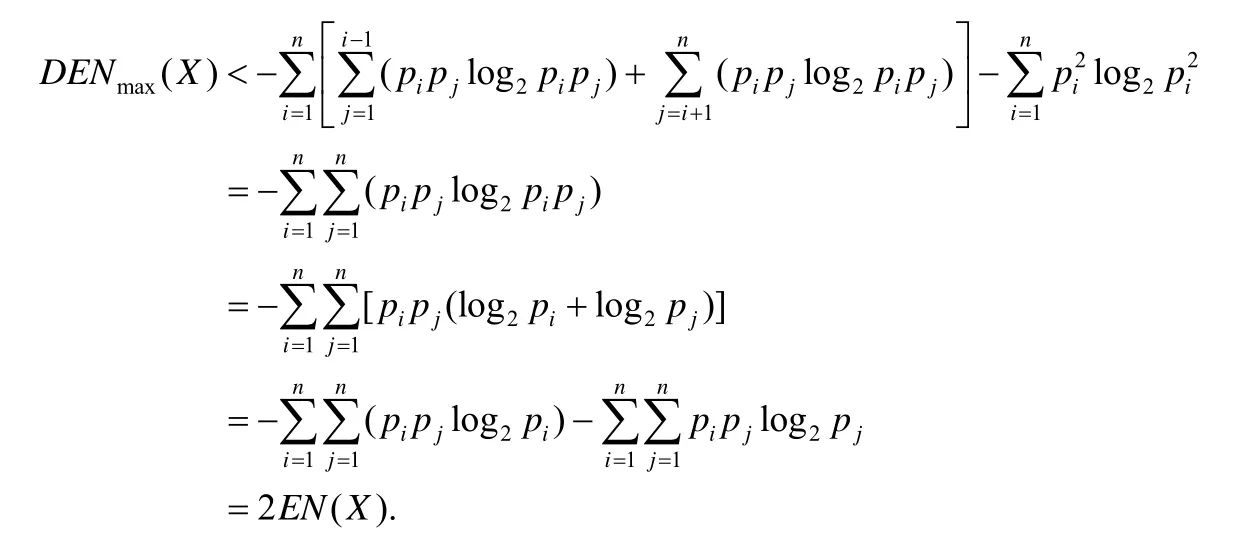
因此我们可以知道,随机变量X的差分熵的最大值小于2 倍的X熵值,即:

情况3.对于更一般的情况,2n-1＜C＜n2-n+1.考虑情况2,Y的取值个数是n2-n+1,此时矩阵Dp中,除去主对角线的元素,其余的每一个元素都对应Y的一个不同的取值的概率.而我们现在讨论的一般情况中,C＜n2-n+1,因此这种情况下,矩阵Dp中,除去主对角线的元素,一定存在2 个或多个元素表示同一个差分值的概率的情况.所以,对于一般情况的差分变量Y,可以通过情况2 对应的Y通过合并操作得到.根据定理2,合并操作会使熵值减小,因此,对于更一般的情况:

然后我们考虑情况1.情况1 对应的差分概率矩阵中,位于同一条斜线的元素表示同一个差分值的概率,而这里讨论的一般情况,Y的取值个数是大于情况1 中Y的取值个数.说明这里对应的差分值矩阵中位于同一条斜线上的元素值不再相等.因此,一般情况的Y变量可以看做是由情况1 中的Y变量通过拆分操作得到.根据定理2,拆分操作会使熵值增大,我们可以得到:

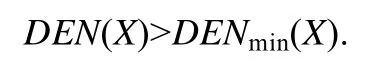
此时,可以得到下面的定理.

定理3.对于离散型随机变量X,不论其数值特性如何,其差分熵DEN(X)都满足下面的式子:

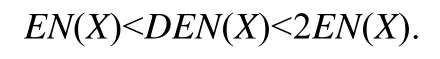
2.4.3 分布特性对差分熵的影响

本节讨论随机变量分布特性对于差分熵的影响.对于更一般的情况分析还有待研究.这里仅考虑特殊情况——二值随机变量,即X可能取的值只有两种,对应概率分别为p和1-p.此时,可以写出X的熵值与差分熵值:

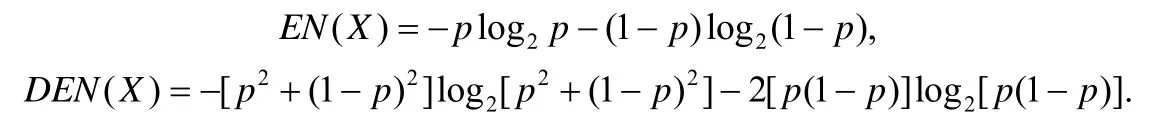
此时,EN(X)和DEN(X)均可以看做是概值p的函数,因此,我们可以采用分析函数的方法分析上面两个式子.

求得导函数如下:

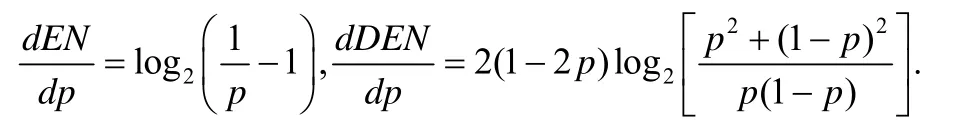
当p=1/2 时,两个导函数同时取0 值,说明均匀分布时,熵值和差分熵值都达到了最大值；同时,当p＜1/2 时,两个导函数均为正值；p＞1/2 时,两个导函数均为负数,这说明当随机变量的分布情况接近于均匀分布时,熵与差分熵最大.

熵值和差分熵值的原函数和导函数图像如图9、图10 所示.

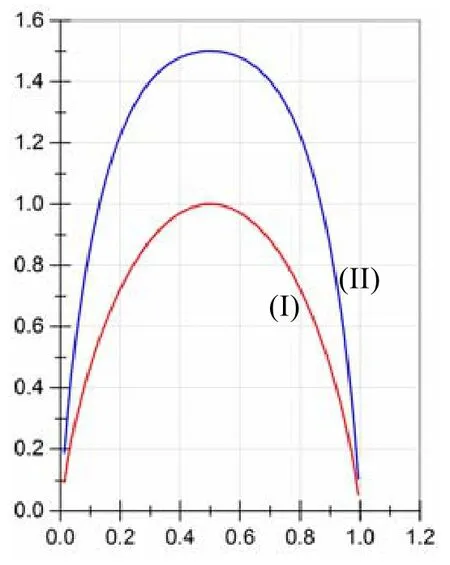
Fig.9 Image of entropy (line I)and difference entropy (line II)for binary random variable图9 二值随机变量的熵值(曲线I)和差分熵值(曲线II)的函数图像

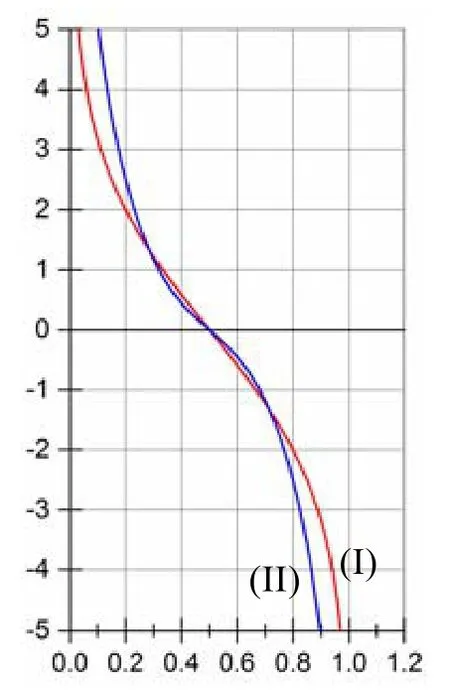
Fig.10 Image of derivative function of entropy (line I)and difference entropy (line II)of the binary random variable图10 二值随机变量熵值(曲线I)和差分熵值(曲线II)导函数图像

可以发现:两个导函数的图像具有3 个交点,3 个交点的横坐标大约是0.3,0.5,0.7(此处0.3 和0.7 为近似值),说明在[0.3,0.7]的范围内,熵值的变化速率比差分熵值要快；而[0,0.3]以及[0.7,1]的范围内,则差分熵值的变化速率更快.

接下来讨论熵值和差分熵值的差距,将它们的差分熵值和熵值做差如下:

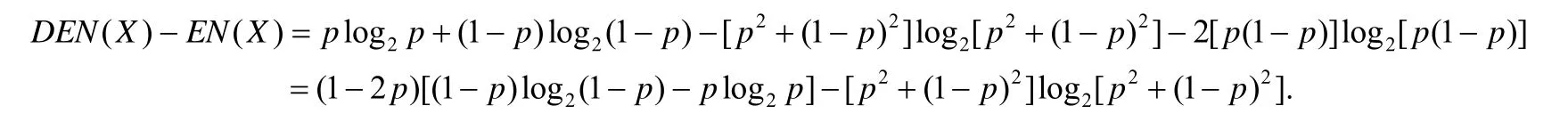
做出以上差值函数图像如图11 所示.

从图11 中可以看到,图像的峰值大约处于p=0.3 和p=0.7 的位置,这两个位置也恰好也是熵和差分熵导函数的交点位置.从总的趋势上来看,中心部分的差值较大,两边则差值较小.这说明随机变量的分布情况越接近于均匀分布,差分熵和熵的差距就越大.

通过以上分析,我们可以得到下面的定理.

定理4.关于离散型随机变量X,具有下面的结论.

(1)X的分布越接近均匀分布,熵值和差分熵值就越大；

(2)X的差分熵值永远大于X的熵值；同时,X的随机性增大时,熵值和差分熵值的差距也在逐渐增大.在平均分布的附近会达到最大值；

(3)如果X的分布接近均匀分布,那么在改变X的概率分布时,熵值比差分熵值对于分布情况变化更加敏感；如果X的分布是倾斜的,不同的取值对应的概率差距很大,那么在改变X的概率分布时,差分熵值比熵值对于分布情况的变化更加敏感.

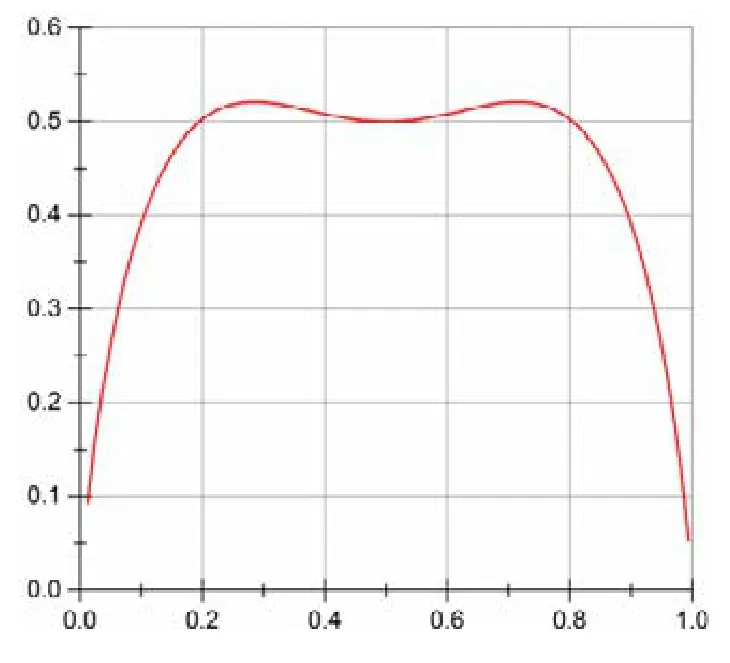
Fig.11 Image of the difference result entropy and difference entropy of binary random variable图11 二值随机变量熵值与信息熵值的差分函数图像

2.5 小 结

本节描述了差分熵的定义以及相关的特性.通过上文的分析可知,差分熵会同时受到数据的数值特性和分布特性的影响,并在某些情况下,差分熵值对于数据特性变化表现出了更高的敏感度.

3 基于差分信息熵的网络时序型隐蔽信道检测算法

本节提出基于差分信息熵的网络时序型隐蔽信道检测算法.首先需要说明的是:Cabuk 和Gianvecchio 提出的算法均假设正常数据的随机性比隐蔽信道数据大[21,30],但是笔者认为,正常信道的特征取决于实际的网络环境,如果网络通畅,数据包的间隔的抖动可能会很小,此时包间隔数据的随机性也就会很小.因此,我们不可以对正常网络的数据特征进行任何的假设,而应该通过实验对正常数据进行特征提取,然后从待测数据中提取特征后,与正常数据的特征做比对,决定其中是否包含隐蔽信道.

基于以上的思想,设计基于差分信息熵的网络时序型隐蔽信道检测算法的思路如下.

(1)收集网络中包时间间隔数据,构造时间间隔序列:{s1,s2,...,sn}；

(2)数据分类,根据一定的规则,将数据划分为m类,记作c1,c2,...,cm,并对每一个类赋予一个代表该类数据的数值:v1,v2,...,vm.分类后,同一个类中的数据不加区别,统一用该类的代表数值来表示.分类后的序列表示为{t1,t2,...,tn},其中,si∈cj→ti=vj；

(3)将分类后的序列划分成大小为w的多个子窗口,如果采集到的数据量为n,那么可以划分的窗口个数为,并经每个窗口中的序列记作:{ti,1,ti,2,…,ti,w}；

(4)计算每个窗口的熵值ENi.统计窗口中每个数值出现的比率,计算熵值,其中,cnti,j表示检测窗口i中属于cj类的数据的个数；

(5)计算每个窗口序列的差分序列,记作:{pi,1,pi,2,…,pi,w-1},其中,pi,j=ti,j-ti,j+1；

(6)计算每个窗口的差分熵值,记作DENi.根据上一节的分析,对原始数据划分m类后,差分运算后的数据最多有m2-m+1 类,最少则有2m-1 类.这里记差分运算后的数据类簇个数为m′,并将差分值的各个类簇记作,然后计算差分熵值,其中,表示检测窗口i中属于dj类的差分值的个数；

(7)将每个窗口的计算结果和正常信道的对应结果EN0以及DEN0比较,根据给定的偏差值εE和εD,如果|ENi-EN0|≤εE并且|DENi-DEN0|≤εD,说明当前检测窗口的数据中没有隐蔽信道；否则,可以认为当前检测窗口的数据可能包含隐蔽信道.

以上是算法的基本思路.

4 算法实现和参数设定

本节说明算法在实现过程涉及到的一些参数确定,我们将通过实验来确定最优的参数设定方案.通过前文对于算法原理的描述可知,待确定的参数值有:划分类簇的个数m、每个类簇的代表值vi、窗口大小w以及正常信道的阈值EN0,DEN0和对应的偏差值εE和εD.下文中,我们首先分析正常数据的特点,然后确定这些参数值.

4.1 正常信道数据分析

我们通过程序实时抓取网络数据包,统计包时间间隔的分布情况.实验结果表明:当前的实验室环境下,网络数据包的时间间隔主要分布在(75,1075]范围内.这里,为了便于数据分析,我们将数据包间隔的范围划分为40个长度为25 的子区间,记作R1,R2,...,Rn,并将每个区间内数据的频率记作pi.而落在(75,1075]范围以外的数据被认为是离群点,不作为实验数据.统计落在各个子区间内的数据所占比例,如图12 所示.

Fig.12 Bar-chart of the packet interval of legitimate channel图12 正常网络数据包时间间隔统计

接下来,用指数分布(exponential distribution)来描述正常数据包的分布情况,指数分布的密度函数如下:

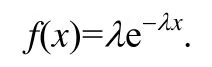
这里涉及到了参数λ,可以采用一阶矩估计法对参数λ进行估计:

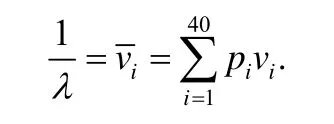
代入我们的实验数据,可以得到:λ≈0.0029.

于是,正常数据包的时间间隔分布的密度函数如下:

4.2 数据离散化

至此,前文中所有的分析和说明都是基于离散型的随机变量,但是在实际网络环境中,数据包的时间间隔可以看做是一个连续型的随机变量.为了便于发现数据的特征,简化数据处理过程,我们首先需要对数据进行离散化,具体方法就是对数据进行分类,将连续型的随机变量按照取值范围划分类簇.数据离散化的过程对应于第3节算法执行步骤中的步骤(2).

数据离散化过程中,划分类簇的个数将会直接影响后续算法的处理效果.划分类簇过少,使得数据中的某些特征丢失；而划分类簇过多,则增加了算法处理的复杂度,影响检测效率.显然,我们知道这样两个事实:划分的类簇越多,就需要越多的测试数据才可以将数据中的特征表现出来,对于差分熵而言,最坏情况下,差分结果的类簇个数会随着原始数据的类簇个数的增长而呈现平方式的增长,如果数据量不够,则会使得计算得到的差分熵值不准确.

图13 给出了对于有5 个类簇均匀分布的情况下,熵值和差分熵值随着样本容量增大时的变化情况.可以看到:一开始,随着样本容量的增大,熵值和差分熵值也在显著增大；而当样本个数大于150 时,熵值开始趋向于稳定；当样本个数大于950 时,差分熵值也在开始趋向稳定.所以可以说:当样本个数大于950 时,样本大小基本不会影响实验结果,此时的结果主要取决于数据本身的特性.这里,我们称可以包含全部数据特征的最小样本容量为有效样本容量(adequate sample size).

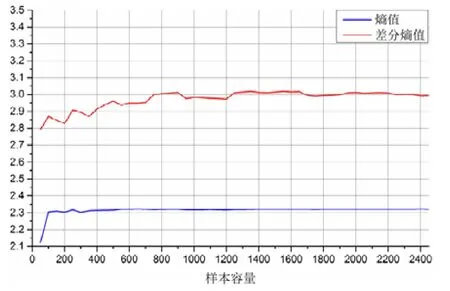
Fig.13 Influence of sample size on the entropy and difference entropy (5 bins)图13 样本个数对于熵值和差分熵值的影响(类簇个数:5)

表2 记录了我们通过实验测试得到的对于不同的类簇个数下的有效样本容量的大小.

Table 2 Adequate sample size of different amount of bins表2 类簇个数与有效样本容量大小

可以看到,划分的类簇个数越多,有效样本容量也就越大.兼顾检测效果和检测效率,我们决定将实验数据划分为10 个类簇；同时,窗口大小设置为1 500.即:m=10,w=1500.

Gianvecchio 在文献[30]提出了一种数据离散化的方式,根据数据包时间间隔的概率分布划分类簇,使得数据落入每一个类簇中的概率相等.作者认为,这样划分类簇的好处是使得程序可以在常数时间内决定采集到的每一个数据项属于哪个类簇.如果将数据划分m类,并用F(x)表示时间间隔数据的分布函数,那么落入每个类簇的概率为1/m；同时,对于某个特定的数值x,可以通过来计算数据落入的类簇.

这里,我们按照正常网络中的数据分布情况来对数据进行等概率划分类簇,类簇个数为10,因此落入每个类簇的概率是10%.我们需要找到正常数据对应指数分布的10%,20%,...,90%的分位点,来确定每个类簇的边界.这样处理的好处是不管正常信道中的包间隔数据的分布情况是怎样的,数据离散化处理后,正常的数据分布情况一定是均匀分布,可以统一处理正常数据的分布特性.这里确定10 个类簇的范围见表3.

Table 3 Binning strategy for data discretization表3 数据离散化划分类簇方案

数据离散化后,落入每个区间的数据均由该区间的代表数值来表示.代表数值通过计算每个区间的平均值得到,对于类簇ci,给定其区间的左右边界ai,bi,可以利用下面的式子计算代表数值vi:

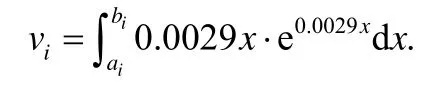
4.3 正常信道数据特征提取

根据上文中的参数设定,我们可以将算法编程实现,提取正常信道的数据特征.这里,我们通过程序实时抓包得到了24 610 个IP 数据包时间间隔数据,共可以划分成16 个大小为1 500 的检测窗口.对于每个窗口的数据离散化后,计算熵值和差分熵值,得到的结果见表4.

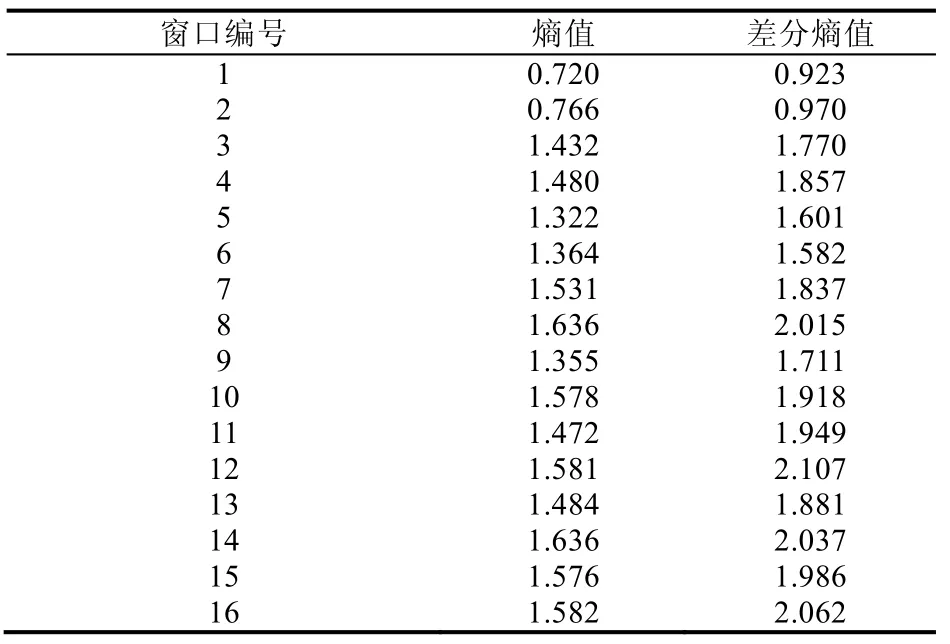
Table 4 Testing result of data from legitimate channel表4 正常信道数据的检测结果

求得各个检测窗口的熵值和差分熵值数据后,可以通过计算这些数据的平均值提取正常信道数据的特征,确定算法中的参数EN0和DEN0的值,得到的结果为:EN0=1.407,DEN0=1.762.

最后确定εE和εD的值.这里,根据3 倍标准差的准则,确定它们的值如下:εE=0.831,εD=1.062.

以上是算法实现过程中的一些参数设定.

5 实验测试及结果分析

本节通过实验检验算法的性能和效果.我们通过程序模拟构建包含隐蔽信道的异常数据,然后用我们提出的算法进行检测,统计检测隐蔽信道的准确率.

5.1 对照实验参数设定

对于对照实验参数的设定,我们将采用4 种检测算法作为对照组,分别是Cabuk 提出的ε相似度算法和随机性检测算法、Gianvecchio 提出的CCE 算法以及熵评估算法.这里需要说明的是,熵评估算法是指直接考察待测数据的熵值大小来判定待测数据中是否包含隐蔽信道(即:计算待测数据的熵值低于指定阈值,则认为待测数据包含隐蔽信道).Gianvecchio 在其实验中将熵评估算法作为CCE 算法实验的对照实验,进而说明CCE 算法的先进性.在这里,熵评估算法也是我们提出的差分熵算法的一部分,因此,这里也效仿Gianvecchio 的做法,将熵评估算法作为实验的对照组,验证差分信息熵算法的效果.通过对照实验,评估差分熵在检测隐蔽信道过程中的作用.利用本文提出的差分熵检测算法与以上4 种检测算法对同样的数据进行检测,通过对比检测结果,评估本文提出的算法的性能和效果.以上4 种算法的实现原理前文中已有说明,这里主要说明算法中相关参数的设定.

· 随机性检测

随机性检测算法通过考察待测数据标准差变化情况,来判定待测数据中是否包含隐蔽信道.Cabuk 在提出该算法时,在2 000 的检测窗口下,设定子窗口大小为250 和100 进行了实验.而Gianvecchio 在文献[30]中介绍CCE 算法时,也将随机性检测算法作为对照组,在其实验中,作者同样选择2 000 大小的检测窗口,以100 为子窗口进行了随机性检测算法的对照实验.根据作者给出的实验结果数据,在当前参数设定下,随机性检测算法可以对正常数据和隐蔽信道数据达到很好的区分.基于以上因素,我们选择100 为子窗口大小进行随机性检测算法的对照实验.此时,对于正常数据的16 个检测窗口,每个检测窗口数据均可以通过算法得到15 个不同的标准差值,通过计算任意两个标准差值的相似度值,进而得到105 个数据,计算这些数据的标准差,就是该算法的输出结果.通过计算16 个检测窗口结果的平均值,就可以得到我们实验中用到的对照阈值.我们通过计算,得到该阈值大小为0.07,检测结果低于该阈值的数据均被认为包含隐蔽信道.

·ε相似度

Cabuk 在文献[21]中对于ε相似度算法的测试中,将参数ε设定为0.005,0.008,0.01,0.02,0.03 和≥0.1 共6 种不同的值,并将算法检测的阈值设定为μ+σ,μ+1.5σ,μ+2σ,Max 共4 种不同的值,其中μ,σ,Max 分别表示ε相似度算法检测合法数据所得结果的均值、标准差以及最大值.Cabuk 对于上面每一种ε和阈值的组合进行了测试.根据作者给出的实验结果,当检测阈值设定为μ+σ和μ+1.5σ时,对于每一种ε参数的设定,检测效果都比较好.此时,对于隐蔽信道的检测可以达到10%以下的漏检率,对于正常信道的检测则可以达到30%以下的误检率.我们的实验设定参考Cabuk 的实验过程,将ε参数设定为0.02,阈值则设定为μ+1.5σ.通过对正常数据的测试,我们ε相似度算法的对照实验中的测试阈值设定为0.973.测试结果高于此阈值时,被认为可能包含隐蔽信道.

· CCE

对于CCE 算法,Gianvecchio 提出了一种基于树形结构的程序实现方式,使得程序时间复杂度可以保持在O(n·m·log(Q))水平,同时,空间复杂度为O(n·m)[30],其中,n,m,Q分别表示测试的数据总量、考察的最长序列长度以及数据离散化过程中划分类簇的个数.我们在前文中已经对于数据离散化作出说明,这里我们同样设定Q值为10；同时,为了兼顾检测效果和检测效率,我们设定考察的最长序列为10.通过对正常数据的测试,我们可以得到测试结果阈值为0.439.检测结果低于该阈值的数据,均被认为可能存在隐蔽信道.

· 熵评估算法

熵评估算法直接考察待测数据的信息熵值来判定待测数据是否包含隐蔽信道.前文中已经说明,引入熵评估算法作为当前实验的对照组的目的,是对差分熵在隐蔽信道检测中所起到的作用进行更深入地评估,熵评估算法过程是本文提出的差分熵算法过程的子过程.这里的阈值前文中已经给出,大小为1.407,低于该阈值的数据均认为其中包含隐蔽信道.另外,熵评估算法在检测过程中同样需要数据离散化的步骤,离散化的过程与差分熵算法使用的离散化过程是相同的,具体步骤前文中已有说明,这里不再赘述.

可见,我们当前实验的网络环境中的数据包时间间隔的随机性非常小.这一点,和Cabuk 以及Gianvecchio提出的“正常数据随机性比隐蔽信道数据高”的假设是不一致的.正如前文所述,正常信道数据的特征由网络环境决定,我们不可以在没有进行实际测试的情况下,对正常信道数据的特征给出任何的假设.

5.2 实验测试数据的收集

实验中,我们主要对IPCTC,TRCTC,JitterBug 这3 种类型的时序型隐蔽信道的数据进行了检测,这3 种类型的隐蔽信道的实现原理前文已有说明.测试数据通过编程模拟得到.

· IPCTC

Cabuk 在其IPCTC 隐蔽信道的实现中,模拟了IPCTC 隐蔽信道的3 种形式:单一时间间隔、多种时间间隔、含噪声.单一时间间隔的IPCTC 隐蔽信道仅采用了1 个固定的时间间隔值,如要发送比特1,则在该时间间隔内发送一个数据包,否则,发送端保持沉默；多种时间间隔的IPCTC 则采用了多个不同的时间间隔的值,发送端每隔t个数据包就调整一次发送的时间间隔,这里的时间间隔之间的切换方式可以是轮换也可以是随机选择；第3类隐蔽信道则是在信道中引入了噪声.在我们的实验中,共实现了4 种不同的IPCTC 隐蔽信道,其中:单一时间间隔的类型实现了两种,时间间隔分别为20ms 和80ms；多个时间间隔的类型实现了2 种,时间间隔采用{20ms,40ms,60ms}这3 种,时间间隔的切换方式有轮换切换和随机切换两种方式,切换的频率为50,即:每隔50 个数据包,就切换一次时间间隔.对于每一种IPCTC 信道,我们通过程序生成了200 000 条数据.具体情况见表5.

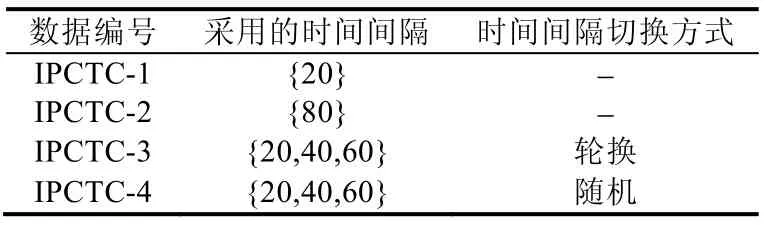
Table 5 Testing data of IPCTC for experiment表5 IPCTC 隐蔽信道实验数据

· TRCTC

TRCTC 隐蔽信道是IPCTC 的改进,其发送数据的时间间隔不再是随意确定,而是通过对合法数据采样得到.用于发送比特0 的时间间隔的集合记作S0,用于发送比特1 的时间间隔的集合记作S1.集合S0和S1互不相交,二者的总和就是合法信道中所有出现过的时间间隔值.这里主要研究了基于不同的比例划分下指定S0和S1集合构成的TRCTC 隐蔽信道.根据S0在全集中所占的比例,我们构建了3 条不同的TRCTC 隐蔽信道,同样对于每一条信道,通过程序生成200 000 条数据.具体情况见表6.

Table 6 Testing data of TRCTC for experiment表6 TRCTC 隐蔽信道实验数据

表中,S0和S1集合中的时间间隔数据通过这样的方式得到:首先统计正常信道中出现的时间间隔值以及每个值出现的频率,然后根据规定的比例,选择适当的数值构成集合S0,剩余的数值构成S1.

· JitterBug

JitterBug 隐蔽信道的数据通过修改正常信道的数据得到.其中,时间参数ω的选择直接决定了信道的效果.本文提出差分信息熵检测算法的一个目的就是弥补CCE 算法在检测JitterBug 隐蔽信道时的不足.JitterBug 隐蔽信道的检测是我们实验研究的主要内容.下文中,我们取ω值为10,20,30,...,1000 共100 个不同的值,构建了100条不同的JitterBug 隐蔽信道.同样地,对于每一条隐蔽信道,我们会通过程序生成200 000 条数据.

与差分熵算法的参数设定相同,实验中作为对照实验的4 种算法在检测时也将检测窗口确定为1 500,因此,200 000 条数据就可以构成133 个检测窗口.

5.3 实验结果及分析

5.3.1 IPCTC 隐蔽信道检测实验结果

表7～表11 分别显示了ε-相似度算法、CCE 算法、随机性检测算法、熵评估算法以及差分熵算法对于IPCTC隐蔽信道的检测效果.表中给出了算法检测133 个检测窗口数据所得结果的平均值和标准差以及每个算法判断规则下的检测率.表7 给出了各个窗口中小于ε参数的相似度值比例的均值和标准差；表8 给出了CCE 算法检测得到的每个窗口的熵率值的均值和标准差；表9 给出了每个窗口的随机性检测结果的均值和标准差；表10 给出了各个窗口熵值的均值和标准差；最后,表11 给出了差分熵检测算法检测得到的熵值和差分熵值的均值和标准差.

Table 7 Testing result of ε-similarity algorithm in IPCTC data表7 IPCTC 隐蔽信道检测实验ε相似度算法检测结果

Table 8 Testing result of CCE algorithm in IPCTC data表8 IPCTC 隐蔽信道检测实验CCE 算法检测结果

Table 9 Testing result of randomness testing algorithm in IPCTC data表9 IPCTC 隐蔽信道检测实验随机性检测算法检测结果

Table 10 Testing result of entropy testing algorithm in IPCTC data表10 IPCTC 隐蔽信道检测实验熵评估算法检测结果

Table 11 Testing result of difference entropy algorithm in IPCTC data表11 IPCTC 隐蔽信道检测实验差分熵算法检测结果

可以看到,差分熵算法的检测效果明显好于ε相似度算法、随机性检测算法以及CCE 算法.主要原因在于其他两种算法都是假设正常数据的随机性比隐蔽信道数据高,因此两种算法的策略都是检测结果低于阈值时判定待测数据中包含隐蔽信道.我们通过实验证明事实并非如此,在较为流畅的网络环境下,信道中的数据流动相对稳定,此时信道中的数据包传输速率也比较均匀,数据包的时间间隔也基本上为恒定值,随机性较小.本文提出的算法不再对正常信道的特征做出假设,将算法处理的结果作为信道的一种特征,通过待测数据和正常数据特征的差异程度来判定待测数据是否异常,而并非通过量化的大小关系来确定是否包含隐蔽信道,因此检测的准确率较高.

另外,从表中数据还可以看到:尽管熵评估算法是本文提出的差分熵算法的子过程,但是熵评估算法的检测效果和差分熵算法有很大的差别.我们通过实验发现:仅仅通过评估信息熵值,对于正常数据和隐蔽信道数据已经可以达到很好的区分能力.然而,Gianvecchio 在文献[30]中描述的熵评估算法依然采用比较阈值的方式来决定检测结果,基于作者“低于阈值的数据包含隐蔽信道”的思路,导致熵评估算法的检测准确率很低.实验中,我们还将熵评估算法进行了改进,将判定数据是否包含隐蔽信道的标准修改为|ENi-EN0|≤εE,即采用差分熵算法的部分判定标准,此时,熵评估算法对于4 组IPCTC 隐蔽信道的检测率分贝为5.03%,95.72%,92.30%以及93.43%.该结果同样低于差分熵算法,主要原因是信息熵对于待检测数据的分布特性的评估比较充分,而对于待测数据的数值特性的评估能力比较欠缺.则也说明了采用差分信息熵在隐蔽信道检测过程中作为评估标准的必要性.

从实验数据可以看出,当选择单一的时间间隔,并且时间间隔较小时,产生的隐蔽信道的数据特征会和正常信道的数据特征很相似,检测的难度就会加大.对于IPCTC-1 这组数据,3 种检测算法的效果都不太理想.当增加IPCTC 信道中的传输时间间隔,或者引入多个可选的时间间隔时,数据的随机性会显著提高.Cabuk 认为,引入多个时间间隔可使IPCTC 隐蔽信道的隐蔽性增强[21],这个结论的依据是假定正常数据随机性较高.通过上文的实验结果可以看出:3 个算法对于IPCTC-3 和IPCTC-4 这两组数据的检测准确率反而比前面两组数据更高一些.

5.3.2 TRCTC 隐蔽信道检测实验结果

表12～表16 总结了TRCTC 隐蔽信道检测实验的结果.

Table 12 Testing result of ε-similarity algorithm in TRCTC data表12 TRCTC 隐蔽信道检测实验ε相似度算法检测结果

Table 13 Testing result of CCE algorithm in TRCTC data表13 TRCTC 隐蔽信道检测实验CCE 算法检测结果

Table 14 Testing result of randomness testing algorithm in TRCTC data表14 TRCTC 隐蔽信道检测实验随机性检测算法检测结果

Table 15 Testing result of entropy testing algorithm in TRCTC data表15 TRCTC 隐蔽信道检测实验熵评估算法检测结果

Table 16 Testing result of difference entropy algorithm in TRCTC data表16 TRCTC 隐蔽信道检测实验差分熵算法检测结果

TRCTC 采用的数据包时间间隔来自正常数据的采样结果,因此在数值特征上,TRCTC 数据和正常信道数据有类似之处.但是TRCTC 的主要问题在于没有考虑到每个时间间隔数值在正常信道中的分布情况.实验中,我们根据集合S0和S1中的数据在正常信道中的比例构建了3 组TRCTC 隐蔽信道数据,从实验结果中可以看出:构建集合S0和S1使得正常信道中的数据落入两个集合的概率相等时,数据的特征和正常信道的数据最相似,所以相比另外两组数据,5 个算法对于TRCTC-3 这组数据的检测结果都更接近于正常信道.但是其结果依然和正常数据有较大的差异,原因在于S0和S1的二类划分仅仅是一种粗粒度的划分,同在S0集合中的数据在正常数据中出现的概率也可能是不同的,但TRCTC 没有在构建信道时没有考虑到这一点,因此在统计特性上依然会表现出和正常数据较大的差异.

同样可以很明显地看出,差分熵检测算法在TRCTC 隐蔽信道的检测上有非常好的效果.对于ε相似度算法和CCE 算法,TRCTC 隐蔽信道的数据也表现出了和正常数据不同的特征,检测结果表明,TRCTC 数据的随机性要比正常数据高.这和两个算法中“隐蔽信道数据的随机性低于正常信道数据”的思想是相悖的,因此检测的效果不理想.

观察表14 还可以发现,随机性检测算法对于3 种TRCTC 隐蔽信道的检测结果和正常信道非常接近.这说明随机性检测算法对正常信道和TRCTC 隐蔽信道的区分能力很低,而检测结果却好于该算法在IPCTC 隐蔽信道的实验效果,我们通过实验发现:就区分能力而言,随机性检测算法对于IPCTC 隐蔽信道的识别能力更高,然而,基于正常信道随机性高的假设使得该算法在IPCTC 数据中表现较差.这也再一次说明了在没有进行实验验证的情况下,对于正常信道数据情况进行假设的做法是不可取的.

对于熵评估算法,这里可以得到和IPCTC 实验类似的结论.由于我们的实验环境中正常信道的随机性很低,我们的实验结果中,正常信道的熵值低于隐蔽信道数据,因此熵评估算法的检测率很低.通过我们改进后的熵评估算法得到的检测率为92.43%,95.25%,97.32,同样低于差分信息熵算法.

5.3.3 JitterBug 隐蔽信道检测实验结果

IPCTC 将要传输的隐秘信息转换为指定的时间区间内是否发送数据包的事件,IPCTC 产生的数据包间隔完全没有参照正常数据,因此得到数据的可能会呈现出和正常数据完全不同的特征；TRCTC 数据中的数值通过正常数据采样得到,因此TRCTC 的数据和正常数据具有相似的数值特性,但是TRCTC 在构建信道过程中忽视了通过采样得到的每个数值的出现概率,这将导致TRCTC 的数据呈现出不同于正常数据的统计特性.所以,IPCTC 和TRCTC 的抗检测能力都比较差.

JitterBug 隐蔽信道通过对正常数据包的时间间隔做出细微的修改来编码隐秘信息.选择合适的参数ω的值,就可以尽可能小地减少构建隐蔽信道过程中对于正常数据统计特性的影响.因此,JitterBug 隐蔽信道具有比IPCTC 和TRCTC 更强的抗检测性.但是由于JitterBug 的数据包间隔均为ω/2 的倍数,因此JitterBug 产生的包间隔数据具有较为明显数值特性,因此就可以利用这样的特征来检测JitterBug 隐蔽信道.

对JitterBug 隐蔽信道的检测是我们重点要研究的内容.实验中,我们为参数ω赋予不同的值,得到了100 组不同的JitterBug 隐蔽信道数据,然后比较3 个算法对这100 组数据的检测效果.

ε相似度算法的检测结果如图14 所示.

从图中可以看出,随着参数ω值的增大,小于ε参数值的相似度值比例也在逐渐增加；并且在ω处于[10,340]范围内时,ω的变化会显著影响ε相似度算法的检测结果.产生该现象的主要原因是:当ω的取值较小时,得到的JitterBug 数据的特征主要依赖于构建该隐蔽信道的原数据的特征；随着ω值的增大,JitterBug 的数据特征将同时受到ω值和原数据特征的影响；而当ω值继续增大时,原数据特征对于产生的JitterBug 数据的影响在逐渐减弱,因为更大的ω值意味着原始数据中更多的不同的值在构建JitterBug 过程中映射到了同一个值,因此,数据的随机性在下降,数据之间的相似度也就逐渐在下降,于是就有更多的相似度值小于参数ε.

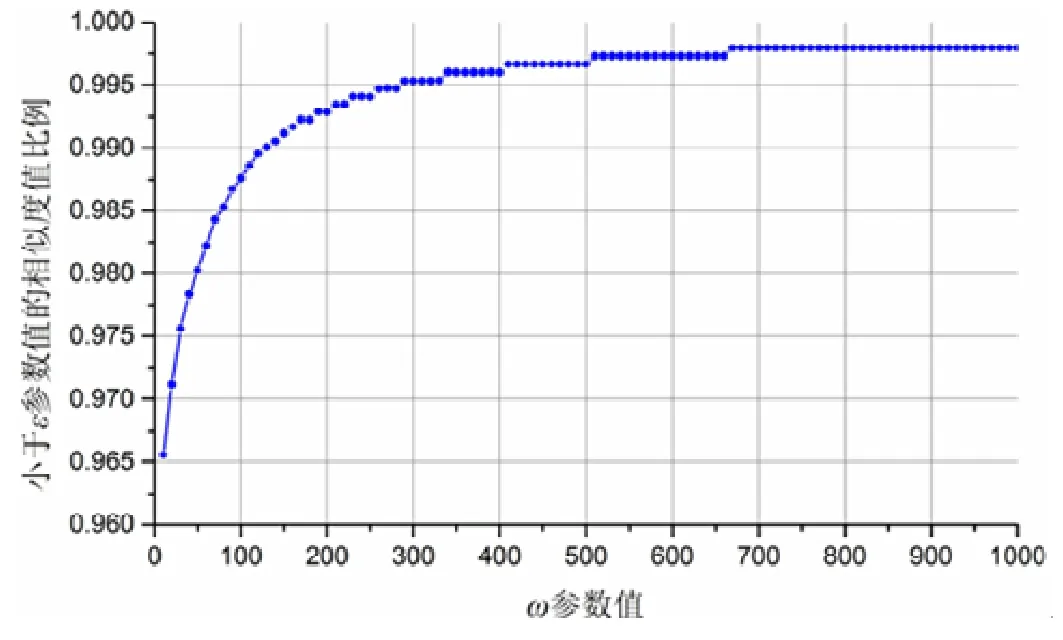
Fig.14 Results of ε-similarity algorithm in JitterBug图14 JitterBug 隐蔽信道检测实验ε相似度算法检测结果

基于正常信道检测得到的阈值为0.973、高于该阈值的检测结果被认为包含隐蔽信道的思路,我们可以看到:当ω值大于50 时,ε相似度算法可有效地检测出JitterBug 隐蔽信道；ε值小于50 时,算法对于JitterBug 隐蔽信道的识别能力很低.然而基于常理推断,ω值很大时,隐蔽信道数据的异常特征更加明显.因此,过大的ω构建的隐蔽信道实用性并不强,我们更关注算法对于ω值较小时生成的JitterBug 隐信道的检测效果.

随机性检测算法对于JitterBug 隐蔽信道的检测结果如图15 所示.

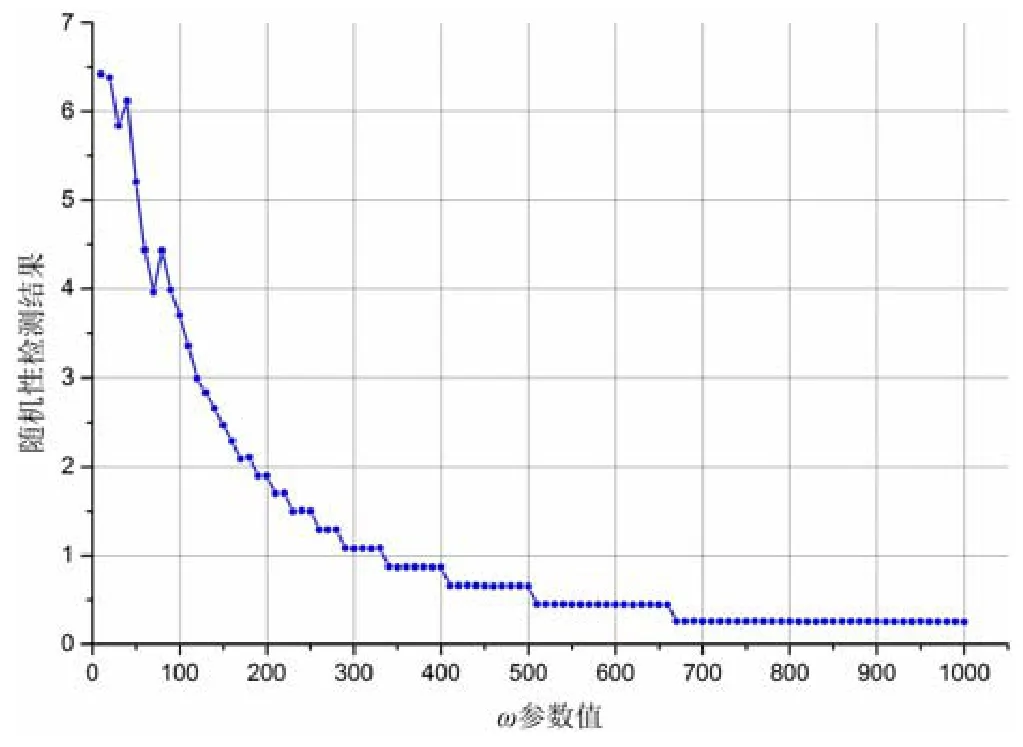
Fig.15 Results of randomness testing algorithm in JitterBug图15 JitterBug 隐蔽信道检测实验随机性检测结果

从实验结果中可以看出:随着ω值的增大,随机性检测算法的检测结果在逐渐减小.然而通过观察实验结果,当ω取值为1 000 时,实验结果取到最小值,然而其值仍然大于检测阈值0.07.这充分说明随机性检测算法对于JitterBug 隐蔽信道的检测能力不足.事实上,当ω值很大时,随机性检测算法对于正常数据和JitterBug 隐蔽信道数据的识别率很高.而在实际应用中,过大的ω值会减慢JitterBug 隐蔽信道的传输速率,同时也更有可能暴露其异常数据的特征,因此,过大的ω参数设定下生成的JitterBug 隐蔽信道并不实用；较小的ω参数值生成的JitterBug隐蔽信道同时具备高传输速率和高隐蔽性的特征,随机性检测算法对于这样的JitterBug 数据的识别能力是可观的.然而,由于算法定义小于阈值的数据为隐蔽信道数据,这就为算法识别隐蔽信道数据造成了误导,这里再一次证明了正常数据随机性高的假设是不合理的.

图16、图17 分别描述了CCE 算法和差分熵算法对于JitterBug 隐蔽信道的检测结果.

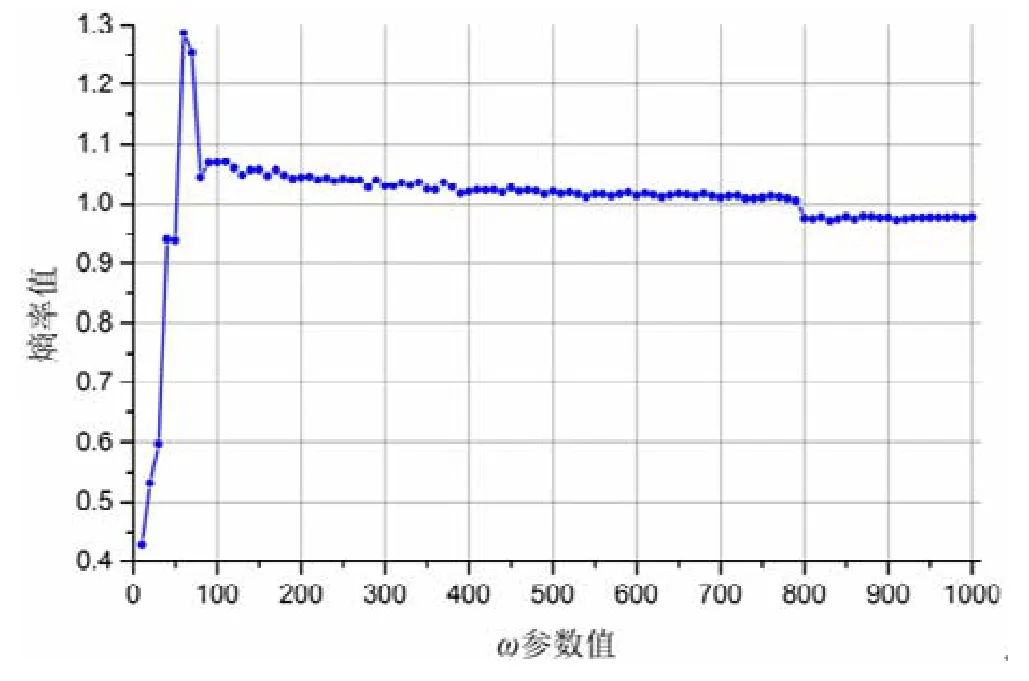
Fig.16 Results of CCE algorithm in JitterBug图16 JitterBug 隐蔽信道检测实验CCE 算法检测结果

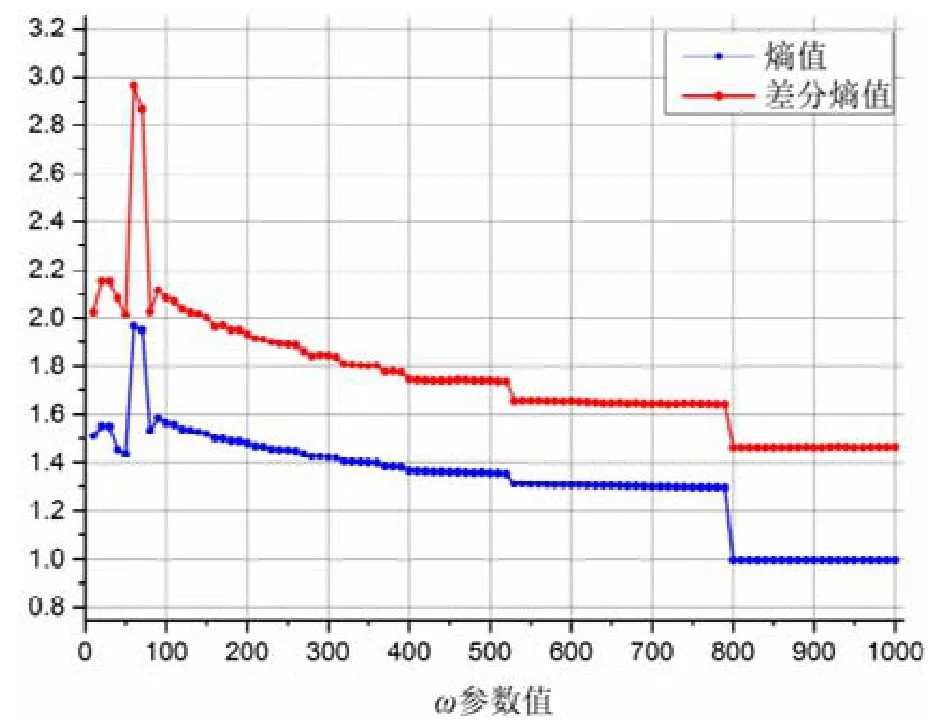
Fig.17 Results of difference entropy algorithm in JitterBug图17 JitterBug 隐蔽信道检测实验差分熵算法检测结果

可以看到:对于CCE 算法得到的熵率值以及差分熵算法得到的熵值和差分熵值,三者图像的形状很相似.产生此结果的原因可能是JitterBug 的数据是通过修改正常数据得到的,因此其分布特征会依赖于正常数据的分布特征.而实验中我们发现,正常数据的随机性较低,根据前文的分析,数据的随机性增大时,差分熵和熵值的差别也在逐渐增大,因此数据的随机性较小时,差分熵值和熵值就会有较为相似的结果.

我们还可以从图像中看出,当参数ω大于100 时,CCE 算法和差分熵算法得到的结果都在随着ω的增加而逐渐下降；但相比差分熵值,当ω参数的值增大时,CCE 算法得到的熵率并未出现很明显的下降趋势.这说明差分熵值对于数据特征的变化更为敏感,这也意味着差分熵算法的灵敏度更高一些.

关于熵评估算法检测JitterBug 隐蔽信道的实验情况,其结果在图16 中已经有所呈现,图中的曲线II 即为不同ω参数设定下的熵值.通过图像可以看到:类似于前面随机性检测算法的实验结果,虽然随着ω参数的增大,检测结果在逐渐减小,当ω参数大于300 后,熵值结果将低于我们的阈值1.40,此时熵评估算法对于JitterBug 隐蔽信道的检测效果比较好.然而,前文中已经说明,过大的ω值构建的JitterBug 隐蔽信道的实用性并不强.因此,对于这些数据检测效果好并没有太大的意义.因此,Gianvecchio 提出的熵评估算法对于JitterBug 隐蔽信道的检测能力比较弱.而改变熵评估算法的评定标准为|ENi-EN0|≤εE后,所有的实验结果均会落在EN0±εE的范围内.根据算法的定义,这意味着所有的数据均会被判定为正常数据,这说明改进判定规则后的熵评估算法依然无法有效地检测JitterBug 隐蔽信道.

最后,根据每个算法判定是否包含隐蔽信道的准则,统计每个算法的检测准确率,如图18 所示.

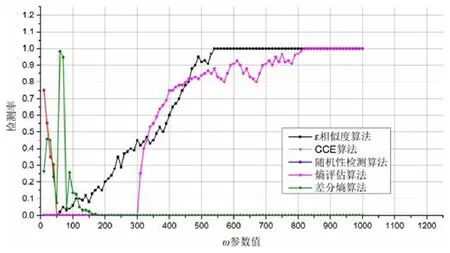
Fig.18 Detecting rate of JitterBug covert channel图18 JitterBug 隐蔽信道检测率

从图中可以看到:ω值大于50 时,ε相似度算法检测效果较好；ω值在60～190 的范围内,差分熵检测算法表现出了较好的检测效果；ω值在0～60 范围内,CCE 算法的检测效果较好；而当ω大于300 后,熵评估算法效果很好.

当ω值大于200 时,CCE 算法和差分熵算法的检测率为0.产生该现象的主要原因是:当ω值远远大于正常数据中的数值时,得到的JitterBug 数据中的数值有很大的概率会落在原始数据的范围之外,此时再进行数据离散化时,就有很大的概率将所有的数据划分到同一个类簇中,于是得到的数据将会是常数序列.就这一点而言,数据离散化的过程会使得原始数据的主要特征丢失,因而导致检测算法失效.这也说明算法的的实现过程中还有一些问题,有待改进.

以上实验证明,差分熵检测算法在检测IPCTC,TRCTC 以及JitterBug 隐蔽信道方面表现出了比ε相似度算法、随机性检测算法以及CCE 算法更好的效果.差分熵检测技术同时考察了待测数据的数值特性和分布特性,检测指标更加严格,能更深入地挖掘数据中存在的特征.对于JitterBug 隐蔽信道,差分熵检测技术可以找到其数据中不同于正常数据的数值特性,从而达到较好的检测效果.相比之下,ε相似度算法和随机性检测算法考察了数据的数值特性,而数据的分布特性在算法对数据进行排序时和计算标准查过程中已经造成了部分丢失；CCE算法和熵评估算法则主要考察了数据的分布特性,忽视了数据的数值特性.因此,这4 种算法在检测JitterBug 中效果不太理想.而熵评估算法那和ε相似度算法虽然在ω取较大值是表现出很好的效果,但是对于JitterBug 隐蔽信道的检测,我们更关注ω取较小值是的情况.

6 总结与展望

本文基于前人的研究成果,提出了一种基于差分信息熵的网络时序型隐蔽信道检测技术.文中首先给出了差分信息熵的概念；然后,通过理论分析总结了一些差分信息熵所具备的性质；然后,提出基于差分信息熵的网络时序型隐蔽信道检测算法,并通过实验证明算法在IPCTC,TRCTC 和JitterBug 隐蔽信道的检测上具有较好的效果.本文所涉及的研究工作还存在一些问题,这也是今后研究工作的主要方向.

(1)对于差分信息熵的研究,目前主要基于离散型随机变量.网络数据包的时间间隔数据从某种程度上可以看作是连续型的随机变量,文中涉及到的数据离散化处理将连续型随机变量转化为离散型,但从实验结果也可以看到,该处理步骤会使得原始数据中的部分数值特性和分布特性丢失,使得检测结果产生误差；

(2)文中对于差分信息熵的部分理论仅仅给出了不完全的分析,更严密、更准确的分析结果还有待研究；

(3)实验测试了新算法对于IPCTC,TRCTC 和JitterBug 这3 种隐蔽信道的检测效果,而对于其他类型的隐蔽信道的效果还需要更多的研究工作.