基于复模态灵敏度分析的制动尖叫控制研究

赵 铎，靳晓雄

(1.同济大学汽车学院,上海 201804；2.天合亚太有限公司，上海 201804)

制动器摩擦导致的制动尖叫对汽车的乘坐舒适性有着重要影响，是工业界和学术界面临的重点和难点问题[1]。全面分析制动尖叫的产生机理和影响因素，并提出针对性的降噪方案，已经成为目前汽车NVH研究的一项重点内容，对于提升制动器零部件噪声性能及整车品质有着重大的理论和工程价值[2-3]。因此，有关制动器尖叫特性的建模仿真、分析控制已成为制动器开发的核心关键技术。

盘式制动器主要部件包括：制动盘、制动钳、制动块、活塞、导向销等，如图1所示。相关部件的摩擦作用将可能导致制动尖叫的产生。

图1 盘式制动器及其主要部件Fig.1 Main components of brake system

制动尖叫机理研究可追溯至1930年，国内外学者进行了大量研究，提出了很多机理，目前，比较主流的理论有:摩擦副特性理论、自锁-滑动理论、模态耦合理论[4]。摩擦副特性理论认为摩擦材料接触特性是导致制动尖叫的根本原因[5-6]，当系统阻尼较小时，系统会产生自激振动现象，从而导致制动噪声。Sprag-Slip理论[7]用于解释制动器结构设计因素对制动尖叫特性的影响，认为摩擦力的变化是由于法向力的变化导致的。

相关学者在对实际制动器结构简化的基础上建立起复模态有限元模型和瞬态动力学模型[8-10]，从理论角度对制动尖叫问题进行定性乃至定量的分析，并尝试对制动尖叫现象进行抑制和消除。大量研究表明，摩擦副材料结构、刚度及阻尼[11]、摩擦系数[12]等因素对制动器制动尖叫影响显著。为定量研究子结构更改设计对于制动器尖叫特性的影响，管迪华等人[11]建立了制动器摩擦闭环耦合有限元模型，基于模态综合法分析各子结构对系统模态的贡献量，分析了子结构模态对系统不稳定模态的影响，然而并未进一步明确如何通过关键参数的优化来确定制动器尖叫的抑制方案。

目前在制动器噪声控制措施方面多基于工程经验，寻优迭代过程工作量大，且尖叫控制效果不佳。因此，如何快速找到导致制动尖叫产生的关键结构参数、并进行结构优化设计是制动器NVH性能优化设计的关键。

本文将针对实际应用过程中盘式制动器出现的制动尖叫问题展开研究。基于ABAQUS有限元软件建立复模态有限元模型进行制动尖叫的预测；针对试验和仿真中出现主要尖叫频率所对应的不稳定模态，展开子结构灵敏度分析，并进一步对子结构开展结构优化设计方案分析，提出抑制方案并进行试验验证，从而为低噪声的制动器开发提供理论指导依据。

1 灵敏度分析理论

1.1 制动器系统动力学模型

制动器系统动力学方程如式(3)所示。

(1)

由于接触表面间节点的摩擦力与相对位移量可用下式表示：

{Ff}=[Kf]{U}

(2)

将方程式(1)、(2)合并，重新整理后，得到如下方程：

(3)

由于受到摩擦力的影响，刚度矩阵[K-Kf]具有非对称性。

对方程(3)进行模态坐标变换，引入模态矩阵[Φ]，其由各子结构模态振型矩阵组合而成，将物理坐标U变换到子结构模态坐标q:

{U}=[Φ]{q}

(4)

经坐标变换后，系统方程为：

(5)

其中，

[Ksys]=[Λ]-[Φ]T[Kf][Φ]

(6)

其中，[Λ]为各子结构模态角频率平方组成的对角阵。

方程(5)的右特征向量矩阵Ψ和左特征向量矩阵[Ω]，满足以下关系：

[Ω]T[Ψ]=[I]

(7)

[Ksys]{Ψi}={λisys}{Ψi}

(8)

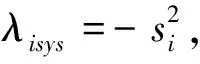
1.2 灵敏度分析指标

就结构动力学系统而言，动力学性能的灵敏度可定义为描述系统性能的特征参数对于系统设计结构参数的改变率。灵敏度分析可分为两类：一是绝对灵敏度，即应变量变化与自变量变化的比；二是相对灵敏度，即相应量的相对变化比值，可以用函数的倒数表示为:

(9)

(10)

其中，S(F)abs、S(F)rel分别为绝对灵敏度、相对灵敏度，F(x)、x分别为应变量、自变量。

1.3 子部件模态频率对系统不稳定模态特征值实部的影响灵敏度

子部件模态频率可以看成自变量，子部件的第j阶模态特征值，会对系统的第i阶模态特征值产生影响。对方程(8)求偏导，可以得到：

(11)

进一步地可以得到：

(12)

子部件模态频率对系统不稳定模态特征值实部的绝对影响灵敏度可以表达为：

(13)

相对灵敏度可以表达为：

(14)

1.4 子部件模态向量对系统不稳定模态特征值实部的影响灵敏度

子部件模态向量可以看成自变量，子部件的第j阶模态向量，会对系统的第i阶模态特征值实部产生影响。

其对系统不稳定模态特征值实部的影响灵敏度可以表示为：

(15)

(16)

相对灵敏度可表示为：

(17)

2 制动器有限元复模态分析

本文研究对象为某轿车右前轮制动器系统，制动器基本参数如表1所示。

表1 制动器基本参数
Tab.1 Basic parameters of brake

制动器类型浮动钳盘式制动器制动盘类型通风盘通风散热筋数目40个制动盘外径240mm制动盘内径140mm制动盘厚度18mm

2.1 模型假设与参数设置

简化假设如下：对系统进行线性化，稳态滑动状态，忽略材料特性的时变性特征

(1)假设制动盘、制动钳、活塞等部件材料为各向同性，制动衬片为各向异性材料。

(2)忽略系统结构阻尼。

(3)假设制动器温度、湿度变化制动材料性能的影响可以忽略。

(4)不考虑制动过程中材料磨损。制动器各零件材料属性如表2所示。

表2 零件材料属性设置表
Tab.2 Material properties of components

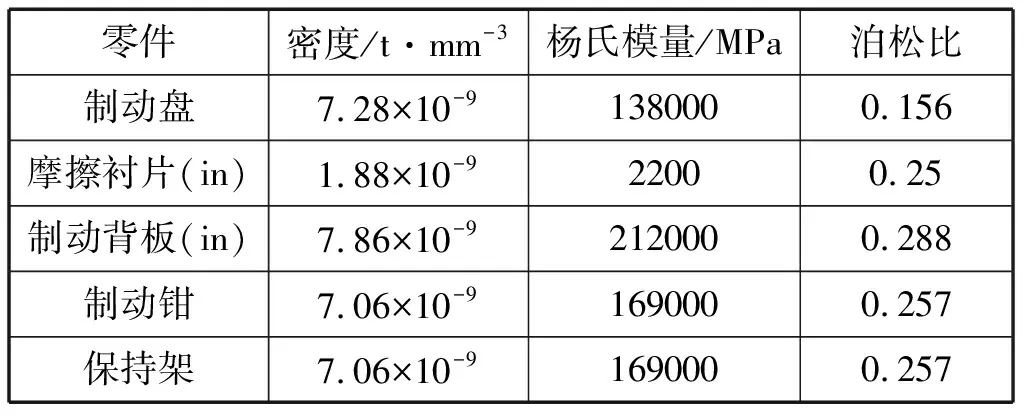
零件密度/t·mm-3杨氏模量/MPa泊松比制动盘7.28×10-91380000.156摩擦衬片(in)1.88×10-922000.25制动背板(in)7.86×10-92120000.288制动钳7.06×10-91690000.257保持架7.06×10-91690000.257

2.2 部件接触及约束设置

图2给出了在ABAQUS中对零件之间相互作用的具体定义。其中，制动盘与摩擦片间、活塞与内摩擦片、制动钳与外摩擦片间连接关系采用面接触定义。弹簧连接器来模拟制动背板与保持架间的接触刚度。基于以上相互作用拓扑关系，建立起如图3所示的制动器系统的有限元仿真模型，模型总的单元总数为31792个。

图2 制动器各零件相互作用拓扑关系Fig.2 The interaction and topological relation of the components

图3 制动器有限元模型Fig.3 Finite element model of disc brake

2.3 分析步设置

在ABAQUS中，利用Step模块来定义五个分析步，具体的分析步设置包括：

(1)在活塞和钳体施加较低制动压力，进行制动器非线性静力分析，以建立制动器初始应力应变状态；

(2)给制动盘施加转速效应，并施加摩擦力，进行非线性静力分析；

(3)通过线性摄动分析进行系统无阻尼、对称系统实模态的提取(0～20000 Hz)；

(4)考虑摩擦耦合效应，通过线性摄动分析，进行非对称系统复模态的提取。

仿真工况设置中，设定活塞制动压力为1～33 bar，在1～10 bar区间，压力间隔为1 bar，10～33 bar区间压力间隔2bar，制动盘转速为0～1200 rpm，制动盘与摩擦衬片的摩擦系数设置为0.37.基于ABAQUS软件进行制动器复模态求解。

2.4 有限元复模态分析结果

基于ABAQUS软件提取了系统不稳定模态的复特征值，如图4所示。特征值实部为正时系统不稳定，实部值越大，系统更趋于发生制动尖叫。图5为制动压力-尖叫频率关系有限元模型仿真与试验结果对比。可以看到，复模态模型能复现试验中出现的大部分尖叫频率，并且尖叫频率频次基本相近，能复现出12.7 kHz附近的尖叫噪声问题。该有限元模型对尖叫预测依然存在“过预测”和“欠预测”问题，欠预测主要是由于CAE模型未考虑实际制动过程中的热机耦合效应和摩擦特性、材料属性的时变性。而过预测主要是由于制动器在特定制动工况下，相关的复模态未被激发出来。

同时，试验和仿真均可以看到，高频制动尖叫现象容易出现在10～30 bar制动压力情况下，尖叫频率基本稳定在3 900 Hz、7 800 Hz、12 700 Hz附近，尖叫频率近似呈现出倍频特点。

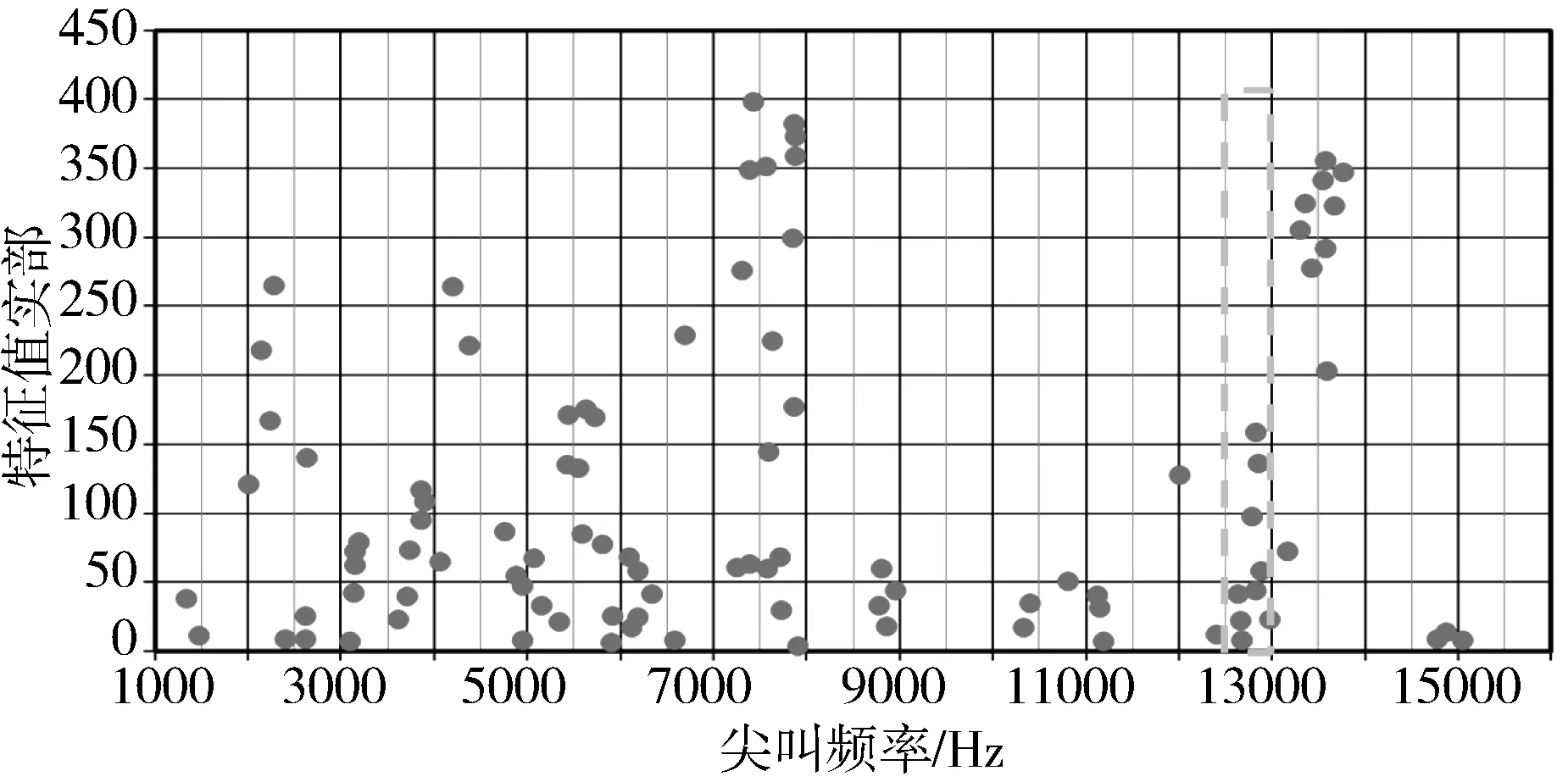
图4 系统不稳定模态复特征值Fig.4 Complex eigen value of unstable modes

图5 仿真与试验对比：制动压力-尖叫频率关系Fig.5 Comparison between simulation and test：relation between brake pressure and scream frequency

2.5 不稳定模态的灵敏度分析

为明确12.7 kHz附近尖叫的主要影响因素，以制动压力30 bar时出现的尖叫频率12 872 Hz对应的不稳定模态为例，进行系统复模态灵敏度分析。图5为系统12 872 Hz尖叫频率下的模态振型、各子结构对系统复模态虚部即尖叫频率的影响灵敏度。

由图6和表3可以看到，系统12 872 Hz不稳定模态实部和虚部，主要受到由系统第52和53阶模态、49和51阶模态等的影响。由图可以看出，第52和53阶模态为制动盘面内径向模态，第49和51阶模态为制动盘面外法向模态。若以(m，n-)描述各阶模态振型节圆、节径数，则第49和51阶模态分别为(0，9)和(0，10)模态。以上对系统不稳定模态影响显著的制动盘各阶模态频率分布在12 497～12 678 Hz之间，均对应制动盘高阶模态。因此，制动盘高阶模态对制动尖叫有着明显的影响。同时，制动钳和活塞对系统制动尖叫的影响亦不容忽略。

推测是由于制动盘、制动钳、活塞三者在尖叫频率12 872 Hz附近产生模态耦合，这也是试验中12.7 kHz发生频率极高的原因。因此，合理地更改这几个零部件结构参数使得相应零部件模态频率分离，理论上可以有效的解决制动器系统尖叫问题。

图6 12 827 Hz不稳定模态及灵敏度Fig.6 Sensitivity of 12 827 Hz unsteady mode

图7 12 827 Hz不稳定模态关键影响因素-子结构模态Fig.7 The key influence factor of unstable mode-substructure mode

表3 零部件模态对系统12872 Hz不稳定模态的灵敏度
Tab.3 The key influence factor of unstable mode-substructure mode

序号子结构模态阶次子结构模态阶次实部灵敏度频率灵敏度1DISC_05312678-0.620.162DISC_052126600.310.073DISC_05112564-0.250.144DISC_049124970.200.135CALIPER_034134530.080.026CALIPER_03012002-0.080.007KNUCKLE_03612677-0.060.008PISTON_007200740.050.019PISTON_00149630.040.0010DISC_046118980.030.02

3 制动盘结构优化

文献[2-3,8]研究表明，在制动尖叫频率区间中制动盘具有多阶结构模态，容易产生模态耦合导致制动尖叫的发生，因此，制动盘模态对于制动器不稳定模态有着重要影响。制动盘作为制动尖叫的主要参与部件，灵敏度分析结果表明对系统不稳定模态影响显著的制动盘各阶模态频率分布在12 497～12 678 Hz之间，均对应制动盘高阶模态。且制动盘面内模态对于制动器不稳定模态实部和虚部影响明显，受径向结构设计方案影响程度较大，而工程设计中通常利用改变制动盘V槽方式对制动器进行尖叫抑制。因此，本节研究制动盘不同的V槽深度对制动盘的尖叫特性的影响规律。分别取原始方案、V槽深度8 mm、10 mm、12 mm、14 mm五个水平，对通风盘式制动器尖叫特性进行研究。

图8 不同水平的制动盘V形槽深度Fig.8 Different levels of brake disc V groove depth

3.1 制动尖叫倾向性指标

所研究制动器的主要关心的尖叫频率范围为F1=7 000～8 000 Hz和F2=12 000～13 000 Hz.定义加权不稳定倾向系数(Weighed Tendency of Instability)，定义如下：

i≠j,Re(Ai)>0,Re(Aj)>0

(18)

其中w1、w2为加权系数，取值分别为0.2和0.8；其中Ai、Aj为系统复特征值实部，Bi、Bj为系统复特征值虚部，即系统不稳定频率，并且Bi∈F1∪F2，Bj∉F1∪F2。由WTOI的定义可知，该评价指标突出了所试验中出现的主要尖叫频率范围的重要性，可以更具针对性地表征制动器的尖叫倾向性。

根据公式(18)，计算具具有不同V槽深度制动盘的制动器尖叫倾向性指标，如所图 9示。可以看到，在不同的系统不稳定倾向性指标变化趋势为：在V槽深度为14 mm时，系统的尖叫不稳定倾向性指标最小。

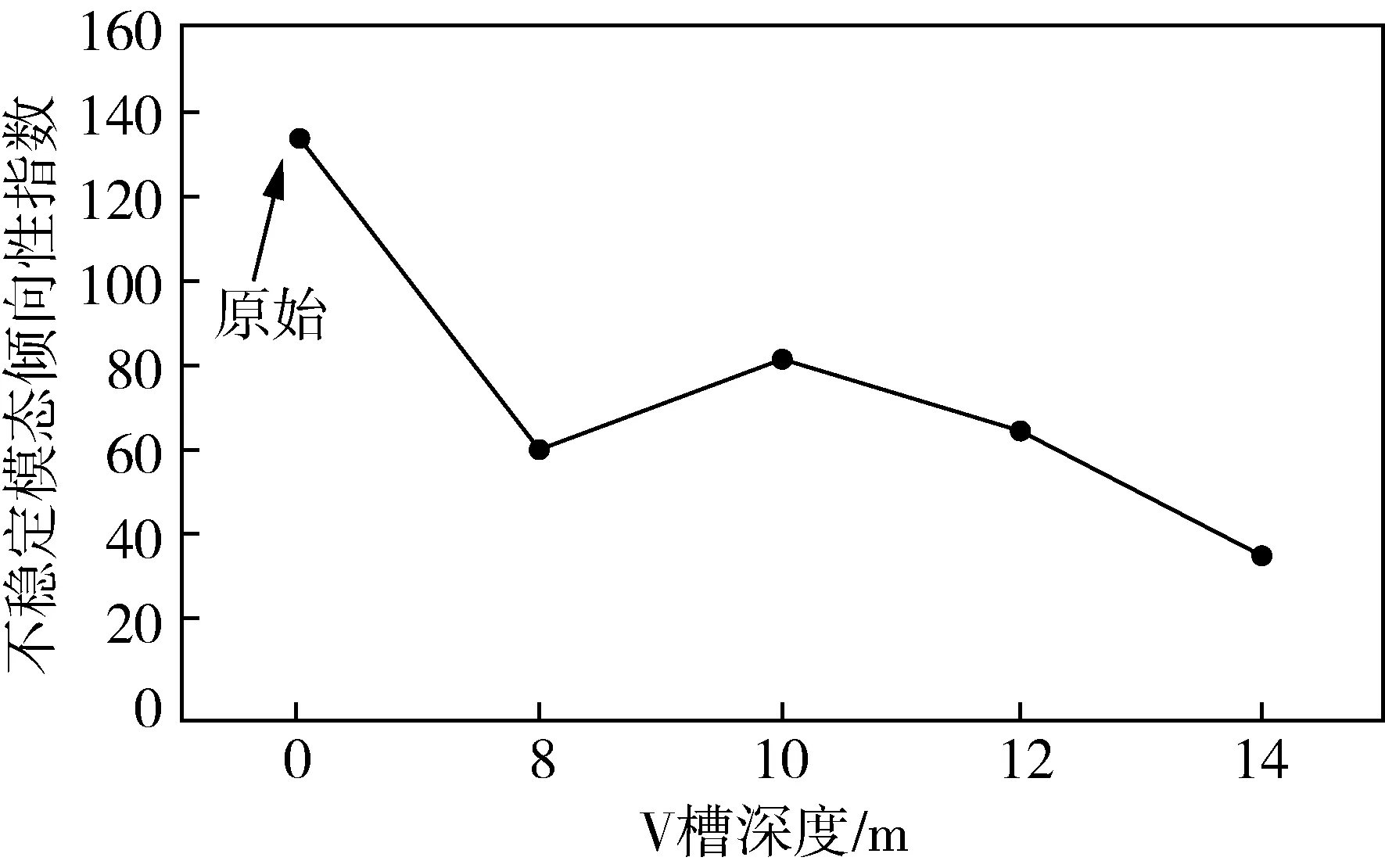
图9 制动盘V槽深度系统尖叫倾向性的影响Fig.9 The effect of the squealing inclination of the disc v-groove depth

3.2 系统复特征值变化

图9为V槽深度14 mm时，系统不稳定模态复特征值变化。可以看到，制动盘开14 mm 深的V槽后，制动器系统在不同的频率范围内，不稳定模态数量及实部均有 明显降低，同时，在尖叫频次较高的12.7 kHz附近，不稳定模态数量显著减小，且模态实部值大大降低。

图10 制动盘V槽深度对系统不稳定模态复特征值的影响Fig.10 The influence of v-groove depth of on complex eigen value of unstable mode

4 优化方案的试验验证

为进行优化方案的尖叫特性验证，基于Link 3900惯量试验台开展优化后制动器制动尖叫特性试验，试验标准为SAE J2521，试验方案和现场如图11所示，测试结果如图 12所示。

可以看到：

(1)优化后制动器尖叫试验结果表明，高于70 dBA的尖叫频率出现率从原方案的56.7%降到2.6%，大于80 dBA尖叫频率噪声出现率降为0.

(2)原制动器12.7 kHz附近的尖叫噪音问题均被消除，制动器噪声性能满足SAE J2521标准。

图11 制动器尖叫测试现场Fig.11 The test scheme for brake squeal

图12 原始方案和优化方案尖叫试验结果Fig.12 Brake squeal test results of he original and the optimized scheme

因此，基于制动盘开V槽深度的优化方案能大大降低制动尖叫的发生概率，实现制动器制动尖叫的抑制，满足制动器低噪声的性能需求。

5 结 论

从关键零部件结构参数角度进行制动尖叫影响因素分析，并提出优化措施。首先提出了尖叫倾向性评价指标，采用参数化分析的方法，对制动盘关键几何参数对系统尖叫特性的影响规律进行了研究。选取了制动盘V槽深度作为设计变量，分析了其对制动器模态振型、尖叫倾向性等指标，提出了制动尖叫问题的快速有效抑制方案，并最后通过试制样机的台架测试试验对优化方案性能进行验证。通过系统尖叫关键影响因素和优化方法的研究，主要得到以下结论：

(1)从有限元仿真的角度，制动盘开V槽可以实现系统不稳定模态的控制，达到不稳定模态特征值实部的减小，不稳定模态数量和尖叫倾向性指标显著降低。在项目关心的12.7 kHz附近，制动尖叫发生几率大大降低。

(2)试验测试结果表明基于制动盘开V槽的优化方案能大大降低制动尖叫的发生概率，实现制动器制动尖叫的抑制，满足制动低噪声的性能需求。

(3)在未来工作中，可深入研究制动块、制动钳、制动盘参数的多变量优化问题，从而进行制动尖叫更有效控制。