圆形支承面上不倒翁的力学特性分析
黄开志 陈小亮 张 龙 田祖安 丁剑平
(重庆科技学院建筑工程学院,重庆 401331)
文[1]采用能量法分析了不倒翁的稳定性,同时得到了其在水平面上摆动时周期,文献[2] 建立了不倒翁纯滚动时的动力学方程,给出了其作纯滚动和能回摆的限制条件,分析了其稳定性,求出了其在水平面上运动时的主要动力学参数计算公式,但未对凸凹支承面上运动时的力学特性进行分析。
本文拟在文献[2]的基础上,进一步优化不倒翁的动力学微分方程和滑动临界曲线以及翻转临界曲线,分析角速度、周期、角加速度、切向反力、法向反力、临界滑动初始摆角、临界翻转初始摆角这些参数与支承面的凸凹性等的关系。
1 动力学微分方程
如图1所示,半径为r,质量偏心距为er的圆形不倒翁,在半径为kr的圆形支承面上作纯滚动。其中,e为不倒翁的质量偏心率;k为支承面半径与不倒翁半径之比。设其在支承面的最高点时与对称轴y轴正好铅垂,则
krφ=rθ
亦即
θ=kφ
(1)

图1 不倒翁的力学模型
对称轴的摆角α满足
α=θ+φ
结合式(1)得
(2)
将式(2)代入式(1)得
(3)
动点O绕定点O′作圆周运动,则
结合式(2)得
(4)
(5)
视动点O为基点,则质心C相对于动点O的加速度
设不倒翁作平面运动,由基点法得质心C的加速度
上式沿坐标轴的投影
不倒翁的动力学微分方程为
由上述3式并结合式(3)~式(9)得
2 临界曲线及运动特性分析
2.1 滑动临界曲线及运动特性
不倒翁不滑动,则其切向反力Ft与法向反力Fn必满足|Ft|≤fsFN,其中fs为静摩擦因数,且fs≥0,FN≥0。
设α0r为临界滑动初始摆角,即当α=α0r时
Ft=±fsFN
(13)
若视滑动临界曲线为点(fs,α0r)的函数ψ(fs,α0r)=0,且设fs轴正向向右,则当点(fs,α)位于该曲线右侧区域时不倒翁作纯滚动,位于该曲线左侧区域时其作滑动。
若视滑动临界曲线为点(k,α0r)的函数ψ(k,α0r)=0,则当点(k,α)位于该曲线与k轴围成的非封闭区域之内时不倒翁作纯滚动,位于该非封闭区域之外时其作滑动。
若视滑动临界曲线为点(k,fs)的函数ψ(k,fs)=0且设fs轴正向向上,则当点(k,fs)位于该曲线上侧区域时不倒翁作纯滚动,位于该曲线的下侧区域时其作滑动。
2.2 翻转临界曲线及运动特性
[mgsinα·(rcosθ-er)-mgcosα·rsinθ]α≤0
结合式(3)上式可简化为
设α0t为临界翻转初始摆角,则由上式并令α=α0t可得翻转临界曲线
(14)
若视翻转临界曲线为点(k,α0t)的函数φ(k,α0t)=0,则当点(k,α)位于该曲线与k轴围成的非封闭区域之内时不倒翁作回摆,位于该非封闭区域之外时其作翻转。
3 求解及主要结果解读
3.1 求解


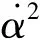

由式(14)可得翻转临界曲线φ(k,α0t)=0。
3.2 算例
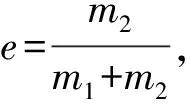
若令g=9.80665m·s-2,r=0.1m,m1=0.3kg,m2=0.2kg,则m=m1+m2=0.5kg,JC=0.0032kg·m2,e=0.4。
按3.1的方法并结合相应的初始条件等,由Maple18可得图2~图10的结果。

图2 α0=π/4时与k的关系
3.3 主要结果解读
图2~图10中,当k>0时表示支承面为凸面,k=±∞时表示水平面,k<0时表示凹面。
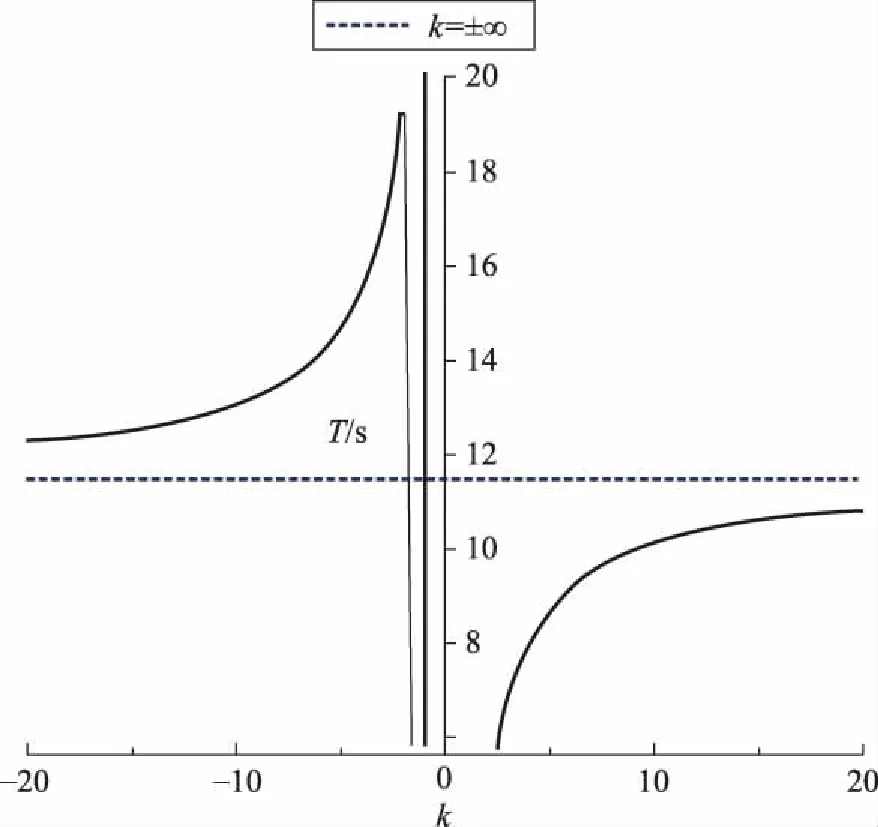
图3 α0=π/4时T与k的关系
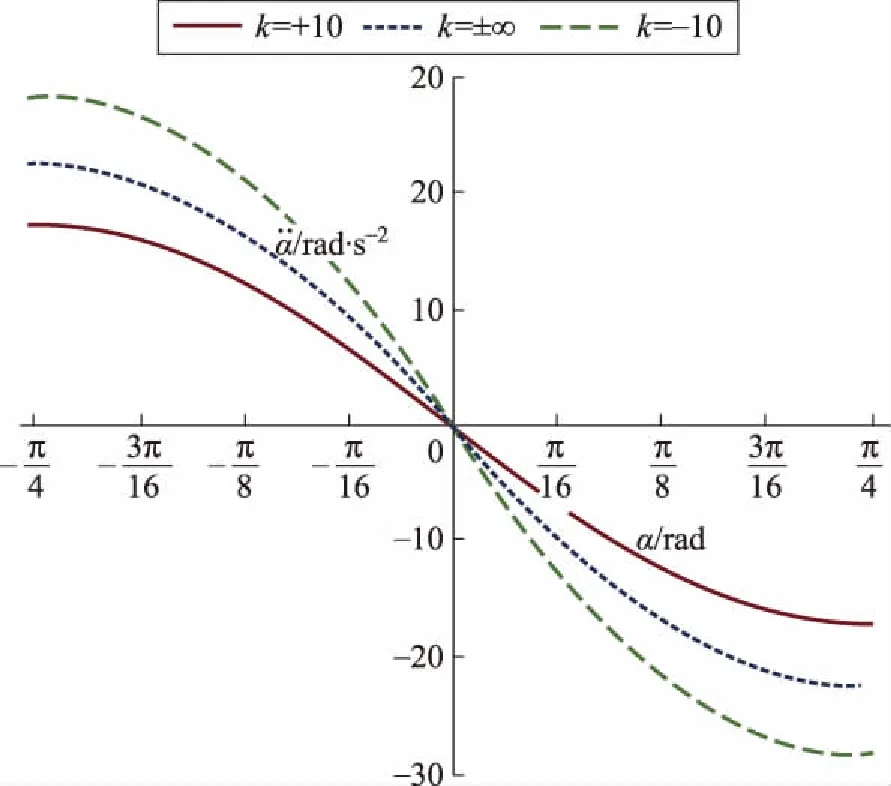
图4 α0=π/4时与k的关系
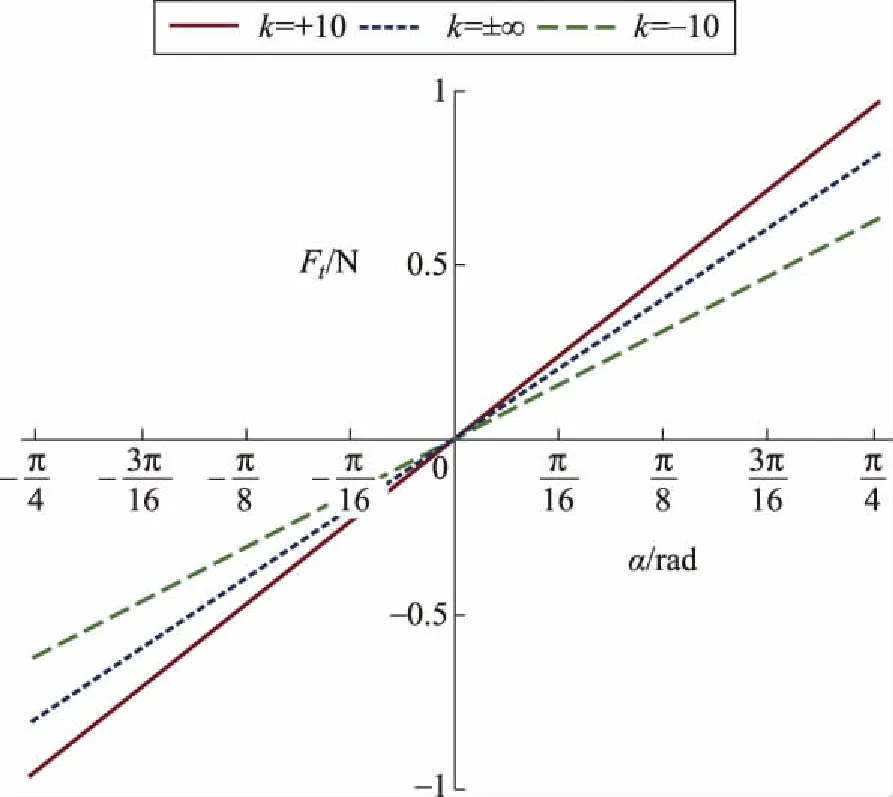
图5 α0=π/4时Ft与k的关系
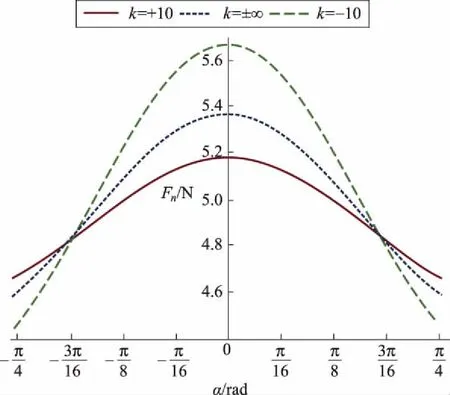
图6 α0=π/4时Fn与k的关系

图7 α0r与fs的关系

图8 fs=0.1时α0r与k的关系

图9 α0r=π/3时所需的fs与k的关系

图10 α0t与k的关系
图3表示周期T与支承面凸凹性的关系。在凸面上,周期随凸面的半径增大而增大,但始终比在凹面上的小;在凹面上,周期随凹面的半径增大而减小。
图5表示切向反力Ft与支承面凸凹性的关系。在凸面上,切向反力随凸面的半径增大而减小,但始终比在凹面上的大;在凹面上,切向反力随凹面的半径增大而增大。
图6表示法向反力Fn与支承面凸凹性的关系。当摆角小于某一值时,在凸面上的法向反力随凸面的半径增大而增大,法向反力比在凹面上的小;在凹面上的法向反力随凹面的半径增大而减小。当摆角超过某一值时,结果正好相反。
图7表示滑动临界曲线ψ(fs,α0r)=0,临界滑动初始摆角α0r随静摩擦因数fs增大而增大,图8表示滑动临界曲线ψ(k,α0r)=0。在凸面上,α0r随凸面的半径增大而增大,但始终比在凹面上的小;在凹面上(图8中未画出),α0r随凹面的半径增大而减小。
图9表示滑动临界曲线ψ(k,fs)=0。在凸面上,临界滑动所需静摩擦因数fs随凸面的半径增大而减小;在凹面上,当凹面的半径小于某一值时,fs随凹面的半径增大而减小,当凹面的半径大于某一值时,fs随凹面的半径增大而增大;当凹面的半径超过某一值时,在凹面上的fs始终比在凸面上的小。
图10表示翻转临界曲线φ(k,α0t)=0。在凸面上,临界翻转初始摆角α0t随凸面的半径增大而增大,但始终比在凹面上的小;在凹面上,α0t已超过π(图10中未画出),即不倒翁始终能回摆。
4 结语
为方便不倒翁类玩具或类似工业产品设计时对其力学特性的分析,本文进一步优化了不倒翁的动力学微分方程和滑动临界曲线以及翻转临界曲线,较详细地给出了各力学参数的计算公式,得到了不倒翁各力学参数与支承面的凸凹性等的关系。
在凹面上,当k∈(-∞,-1)即凹面的半径比不倒翁的半径大时的曲线才有实际意义。
在分析过程中忽略了滚动摩阻等的影响。

