黏附激励下空间目标惯性参数的辨识方法

马卫华，袁大钟，孟思洋，罗建军

(1. 航天飞行动力学技术重点实验室，西安 710072；2. 西北工业大学航天学院，西安 710072；3.上海机电工程研究所，上海 201109)

0 引 言

对空间目标，特别是非合作目标，进行惯性参数辨识是实施后续精准操作的基础，典型的辨识策略大致分为两类，基于视觉测量的非接触式辨识和基于主动激励的接触式辨识。

Aghili[1]针对携带相机的机械臂，建立了基于目标表面特征点信息的非接触参数辨识方法，基于传统运动学模型，采用滤波方法估计目标的姿态参数、转动惯量比以及质心位置。在此基础上，Hou等[2]改进运动学模型，采用对偶四元数重新建模，减少了辨识过程中的计算量。这类辨识方法无需和被测目标发生物理接触，但只能辨识目标的质心位置和转动惯量比，无法给出转动惯量绝对值，以及非常重要的质量信息。

接触式辨识多见于携带机械臂的空间操作机器人，将操作平台和非合作目标通过机械臂物理连接构建为组合体，利用操作平台的主动激励改变组合体线运动和角运动，实施对组合体的惯性特征参数辨识。Yoshisada等[3]详细阐述了基于两大原理(动量守恒方程、牛顿-欧拉方程)的空间非合作目标惯性参数辨识方案，利用线性辨识方程求广义逆完成目标惯性参数辨识。Roberto和Gerhard[4]利用牛顿-欧拉方程，并通过使用加速度计测量来辨识空间非合作目标的惯性参数。

目前很多学者对于目标惯性参数辨识的研究都是基于动量守恒原理，在刚体/挠性体、辨识求解方法等方面开展的。

采用刚体目标假设，Walker等[5]学者引入线动量守恒方程与角动量守恒方程，根据机器人运动学，采用单臂连续运动的激励方式，实现了空间机器人惯性参数的完全辨识； Ma等[6]提出了基于单机械臂主动机动从而辨识本体参数的方法，利用机械臂运动改变本体运动，只需要测量本体的速度、角速度，即可实现空间本体惯性参数的完全辨识，辨识算法简化，实现方案容易；金磊等[7]基于动量守恒原理提出了全增量式(线动量和角动量)的辨识方程，研究了单臂自由飘浮空间机器人抓取未知目标的质量特性参数辨识问题；洪炳镕等[8-9]基于动量守恒原理针对双臂/多臂机器人探讨了其捕捉非合作目标过程中的参数辨识；为提高辨识精度，Chu等[10]学者提出引入末端操作机构的接触力信息，较为准确的反映出操作阶段的运动学、动力学过程，避免常规外界测量误差对系统辨识精度的影响，从而更能准确的描述抓捕作用过程，改善辨识效果。采用挠性体目标假设，何骁等[11]针对大角度机动情况下带挠性附件航天器转动惯量在轨辨识的问题，提出一种将转动惯量参数估计和挠性附件状态估计相结合的并发递推算法。

在辨识求解方法上，除了常规最小二乘法外，徐文福等[12]提出了基于参数解耦的最小二乘法和基于PSO算法的非线性优化两种方法；孙俊等[13]针对传统依赖广义逆求解的辨识方法的问题，诸如辨识过程运算量大、数值容易产生剧烈振荡，造成辨识结果不稳定等，采用基于归一化最小均方(Normalized least mean square, NLMS)准则的Adaline神经网络方法进行空间非合作目标惯性参数的辨识,但需要解决NLMS准则中α，β参数的最优选取问题。显然，优化、智能算法将会进一步应用于目标惯性参数辨识中。

综上可见，仅依赖视觉的非接触辨识方法，无法获得目标转动惯量和质量信息；而接触式辨识中，要求本体必须具备主动激励能力，这对于未装备机械臂之类装置的飞行器，特别是微小型卫星平台而言是较难实现的。

随着微重力环境黏附技术的发展[14]，具备黏附能力的新型飞行器有望形成。这类装有黏附装置的空间飞行器在具有一定相对冲量的前提下，可黏附在目标航天器表面上。而对于空间目标来说，相对冲量是一种自然激励，会导致其运动状态的变化，相当于产生了接触辨识中的主动激励。因此，黏附过程应当具备辨识空间目标惯性参数的潜力。

由于一般情况下黏附过程的激励程度较小，完整辨识目标惯性参数的能力有限。为此，本文基于非接触辨识和接触辨识的特点，提出了基于黏附激励的辨识方法。首先采用视觉非接触辨识方式，建立基于视线信息估计目标惯性参数和相对运动参数的滤波器，并估计黏附前的目标质心和转动惯量比；然后利用黏附激励改变目标运动状态，直接利用非接触方式的滤波器估计黏附后目标(组合体)质心运动速度，并基于动量守恒辨识目标质量参数；最后通过数值仿真完成验证了方法的有效性。

1 黏附前的目标惯性参数辨识

1.1 空间目标的相对方位关系

假设主星携带黏附卫星，并安装有相机来获取目标特征点的位置和视线信息，图1给出了目标和主星的相对位置关系。

借鉴文献[1]中Aghili的研究工作，定义相关物理量及坐标系含义：{A}代表惯性坐标系，原点在主星质心处；{B}代表目标本体系，三轴方向与目标主轴方向平行，原点在目标的质心处；{C}代表目标表面特征点本体系，原点在特征点处。鉴于部分特征点本体系和目标本体系近似重合，为简化问题，在此假设{C}和{B}重合。

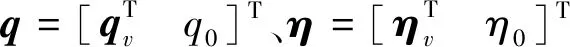
转动惯量比p定义为[1]：

(1)

式中:Ixx,Iyy,Izz为目标的主惯量矩。

因为假设{C}和{B}近似重合，所以本节定义的状态向量数目少于Aghili给出的状态向量，状态方程、观测方程和文献[1]对应模型相比略微简单。后续1.2、1.3、1.4节中的参数模型的具体推导过程可参见文献[1]。

1.2 状态方程

选取目标姿态四元数矢量部分qv、旋转角速度ω、质心r、速度v、转动惯量比p和特征点相对目标质心位置ρ构建状态向量：

(2)

通过对文献[1]状态方程适当简化得到：

(3)

(4)

(5)

其中，

B=diag(bx,by,bz)，

式中：用a×表示矢量a对应的反对称矩阵，ω×即为矢量ω对应的反对称矩阵。

ε表示系统噪声，

(6)

式中:ετ和εf为过程噪声，均定义为标准正态分布的白噪声。

1.3 观测方程

主星可以利用相机获取目标表面特征点的方位信息以及位置信息(均在坐标系{A}中测量得到)，定义测量矢量z为：

(7)

其中:rs为特征点在{A}系中的位置，其模型为[1]：

rs=r+A(q)ρ

(8)

其中:A(q)是从{B}系到{A}系的坐标旋转矩阵，由四元数q确定：

(9)

其中:η为特征点在{A}系中的位置和特征点坐标系姿态指向四元数，近似认为和q相同：

η=q

(10)

式(7)中的ν表示测量噪声，假设为高斯白噪声，协方差R=E[ννT]。

1.4 线性化模型

扩展Kalman滤波要求对非线性状态方程和观测方程(7)作线性化。在文献[1]中相关矩阵基础上，本文直接简化得到对应的雅克比矩阵。

状态方程的雅克比矩阵F为：

(12)

(13)

N(ω)=diag(ωyωz,ωxωz,ωxωy)

(14)

观测方程的雅克比矩阵H

(15)

(16)

联合式(3)、式(7)、式(12)、式(15)，利用扩展卡尔曼滤波基于视觉信息估计黏附前目标质心和转动惯量比。

2 黏附后的目标惯性参数辨识

2.1 黏附后的目标质心速度估计

黏附过程中，目标受到黏附卫星的碰撞后会有两种运动情况：一种是碰撞后彼此分离，沿各自轨迹进行运动；另一种是碰撞后连接形成组合体一起运动。假设黏附能力足够强，黏附卫星和目标形成了组合体，如图2所示。

VT,VS和V′分别为目标黏附前速度、黏附卫星初始速度和黏附后组合体速度；ms，mT分别表示黏附卫星质量、目标星质量；ωr，ω′分别表示黏附前后目标的旋转角速度。

黏附前及黏附后，主星将持续观察目标，借助1.2节的滤波器可以估计黏附后目标的质心速度，估计算法和第1步完全一致。

2.2 基于动量守恒的目标质量辨识

黏附前后满足动量守恒：

mSVS+mTVT=(mS+mT)V′

(17)

该动量守恒方程在主星当地轨道坐标系中是成立的，方程中的速度均是相对速度，数值一般比较小，碰撞前目标和主星保持相对静止，目标速度一般可认为接近0，则上述模型可以进一步简化为

mSVS=(mS+mT)V′

(18)

目标质量的估计模型为

mT=mS(V′TVS)(V′TV′)-1-mS

(19)

如果假设黏附卫星质量、目标质量、黏附卫星速度、目标黏附后速度的测量精度均方差分别用σδmS，σδmT,σδVS,σδV′表示，根据式(18)可以得到辨识后质量的相对精度模型：

(20)

式中:σδmT是目标质量误差的协方差。显然，目标质量相对精度和黏附卫星初始速度有关，随其数值增大而提高，和黏附卫星/目标的质量比也有关，如果二者质量相近，则目标质量估计精度最好，反之则会变差。

3 仿真校验

3.1 仿真设定

3.1.1目标参数和黏附卫星参数

根据文献[1]设定主星部分状态的真值见表1，

论文仿真计算中对应的状态估计初值及部分误差参数也列于该表。

黏附卫星的质量、在目标轨道系初始速度和黏附点在目标本体系下位置分别为20 kg、[0.5 m/s,0 m/s,0 m/s]和[0.25 m，0 m,0 m]。为验证不同质量比下目标质量的辨识精度，目标质量分别设定为2 kg，4 kg，20 kg，80 kg，200 kg，黏附卫星/目标的质量比分别为10，5，1，0.2，0.1。

3.1.2测量与其他仿真参数

目标姿态轨道的动力学/运动学积分步长为0.05 s，测量装置的输出频率2 Hz。测量的特征点位置和方位精度分别为0.045 m(1σ)和0.003°(1σ)。

3.1.3仿真计算流程

完整仿真数据流程如下图所示。

3.2 仿真曲线与分析

3.2.1黏附前的目标特性参数估计

目标转动惯量比估计变化如图4所示,目标质心位置估计误差、质心运动速度估计误差、特征点位置估计误差曲线分别见图5、图6、图7。图4中三条虚线表示标准的转动惯量比，图5～图7中对称分布的黑色曲线为估计误差协方差值(3σ)，考虑到三轴数据类似，图5～图7只提供了X轴数据。

根据仿真结果可见，大概30 s后目标转动惯量比、质心位置、质心速度和特征点位置的估计值分别接近真实值，误差基本在3σ误差协方差曲线以内，误差估计和方差吻合得比较好。表2给出了仿真所得的参数辨识末端精度，对应的三向合成精度分别为0.08 m(1σ)、2.47 mm/s(1σ)、0.0053(1σ)、0.07 m(1σ)。

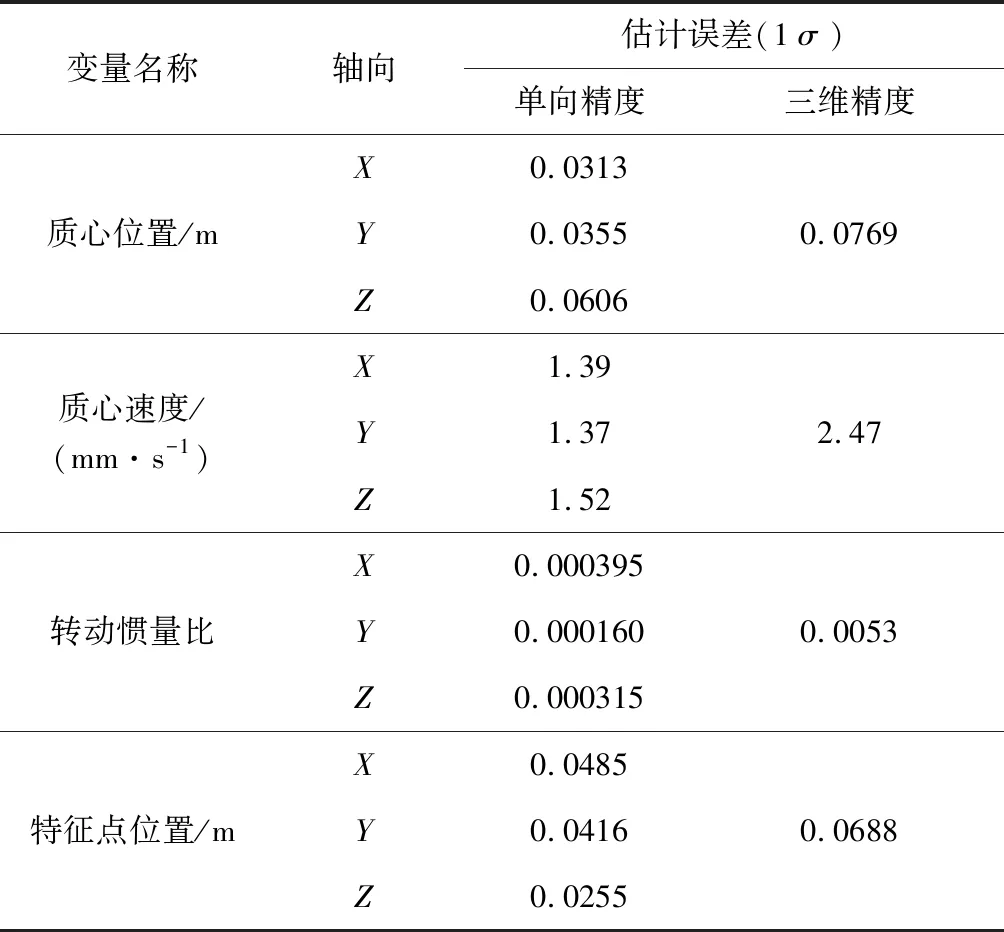
表2 黏附前辨识末端的目标参数精度Table 2 Terminal estimation precision of target parameter before adhesion

基于视觉信息的滤波计算可以较好的估计出目标的质心、质心速度、转动惯量比以及特征点位置等参数。特别是目标质心速度的良好估计，为黏附后黏附过程的目标质量辨识提供了良好的条件。

3.2.2黏附后的目标质量估计

根据式(20)，目标质量估计精度主要取决于黏附卫星/目标的质量比以及目标质心速度精度。

首先估计目标质心速度精度。

主星采用和黏附前相同的滤波器估计组合体质心速度，黏附卫星/目标不同质量比下黏附后目标质心运动速度估计如图8所示，图中对称分布的虚线为估计误差协方差值(3σ)，末端精度统计见表3。图形左端的数字表示黏附卫星/目标质量比。

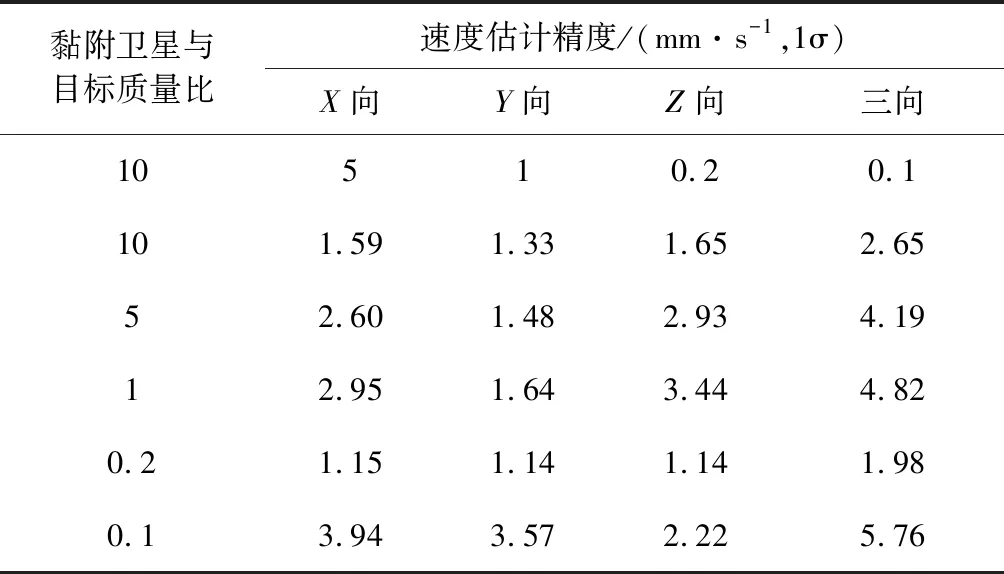
黏附卫星与目标质量比速度估计精度/(mm·s-1,1σ)X向Y向Z向三向10510.20.1101.591.331.652.6552.601.482.934.1912.951.643.444.820.21.151.141.141.980.13.943.572.225.76

从末端精度统计看，组合体质心速度估计精度没有呈现明显规律性变化，各种情况下的精度相差不大，基本可以认为在mm/s量级精度范围，因此可以近似认为目标和微小卫星的质量比变化时，组合体质心速度估计精度是近似相当的。

其次针对不同目标/黏附卫星质量比分析目标质量估计精度。

完成5种工况下的仿真结果，鉴于结果曲线波动形态较为相似，在此仅给出黏附卫星/目标质量比为10和1的仿真曲线，相对误差的统计分析结果展示于表4中。

依仿真可见，依据动量守恒定理计算目标质量时，目标质量估计精度受黏附卫星/目标质量比的影响很明显。两者质量相当时，质量估计精度最高，相对精度大概5%；随着质量差异明显，精度逐渐下降，在比值为1∶10或10∶1时(见图9，图10)，目标质量辨识的相对误差在20%左右。

黏附卫星/目标质量比目标质量估计相对误差/%1∶10201∶5101∶155∶11010∶120

4 结 论

黏附卫星以一定相对速度逼近并黏附于目标，产生可改变目标运动状态的自然激励，文中基于此提出了利用黏附过程的自然激励实施空间目标惯性参数辨识的辨识方法。

相对于常规辨识方法，文中提出的辨识方法仅利用主星视觉测量、充分利用黏附过程自然激励即可实现对目标转动惯量比、质心和质量的辨识，无需常规辨识方法必须的额外主动激励，且辨识过程中算法统一、无需切换，使用更为便捷。

仿真结果证实了所提方法能够实现对非合作目标质心、质心速度、转动惯量比的估计，验证了算法的可行性。

鉴于算法和目标、主星、黏附卫星的初始状态有密切关系，且没有获取目标转动惯量具体数值。后续将对此进行完善，分析算法稳定运行条件，并将辨识约束融入黏附策略设计中。