关于三角形内角一个不等式及其应用

李永利

(河南质量工程职业学院 467001)

近日，笔者发现一个关于三角形内角的分式不等式，经查阅有关资料未见刊载. 本文给出该不等式的证明，并给出几个应用的例子，其中之一为《数学通报》2012年2月号问题2045的加强与拓广.

以下设△ABC三内角A,B,C所对的边长分别为a,b,c，三角形的半周长、外接圆半径、内切圆半径分别为p,R,r.∑表示循环和，∏表示循环积.

定理在△ABC中，有

(1)

当且仅当△ABC为等边三角形时,式中等号成立.

证明由莫尔外德(Mollweid)公式[1]、正切的半角公式

可得

即

同理可得

由以上三式可得

再由恒等式[2][3]

∑a=2p，

∑a2=2(p2-4Rr-r2)，

∑a3=2p(p2-6Rr-3r2)，

∑a4=2(p2-4Rr-r2)2-8p2r2，

∑bc=p2+4Rr+r2，

∏(b+c)=2p(p2+2Rr+r2)，

可得

2(p2-4Rr-r2)2+8p2r2+(2p2-2p2+8Rr+2r2)(p2+4Rr+r2)]

[-2(4Rr+r2)2+2(4Rr+r2)2]}

于是(1)式等价于

(2)

⟺4p2(6R+4r)2≥27(p2+2Rr+r2)2

⟺4p2(36R2+48Rr+16r2)

≥27p4+54p2(2Rr+r2)+27(2Rr+r2)2.

由上式和Gerretsen不等式p2≤4R2+4Rr+3r2可知，欲证(2)式成立，只需证明

4p2(36R2+48Rr+16r2)≥27p2(4R2+4Rr

+3r2)+54p2(2Rr+r2)+27(2Rr+r2)2(3)

⟺p2(144R2+192Rr+64r2)≥p2(108R2+

216Rr+135r2)+27(2Rr+r2)2

⟺p2(36R2-24Rr-71r2)≥27(2Rr+r2)2.

由上式和Gerretsen不等式p2≥16Rr-5r2可知，欲证(3)式成立，只需证明

(16Rr-5r2)(36R2-24Rr-71r2)

≥27(2Rr+r2)2

(4)

⟺(16R-5r)(36R2-24Rr-71r2)

≥27r(2R+r)2

⟺576R3-564R2r-1016Rr2+355r3

≥108R2r+108Rr2+27r3

⟺576R3-672R2r-1124Rr2+328r3≥0

⟺144R3-168R2r-281Rr2+82r3≥0

⟺(144R2+120Rr-41r2)(R-2r)≥0.

而由欧拉不等式R≥2r可知144R2+120Rr-41r2>0，R-2r≥0，于是上式显然成立，从而(4)，(3)，(2)三式成立，故(1)式成立.

以上由证明过程可知，当且仅当R=2r即△ABC为等边三角形时(1)式中等号成立. 定理得证.

下面给出不等式(1)几个应用的例子.

例1在△ABC中，求证：

(5)

(6)

证明由正弦的二倍角公式、余弦和差化积公式和(1)式可得

故(5)式成立.

由余弦的二倍角公式、正弦和差化积公式和(1)式可得

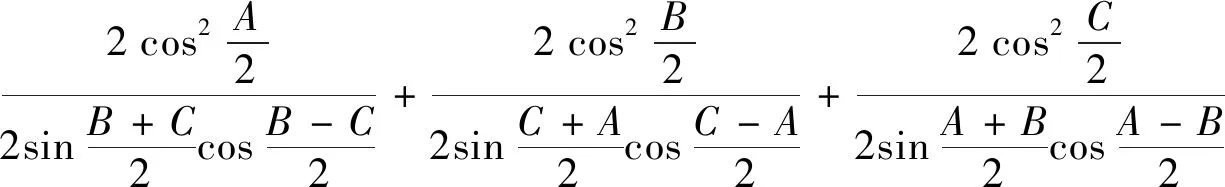
故(6)式成立.

例2在△ABC中，求证：

(7)

(8)

证明按照文[4]中给出的置换方法，在(5)、(6)两式中分别作置换

即可得到不等式(7)、(8).

例3在△ABC中，有

(9)

证明由余弦的二倍角公式和不等式

及不等式(1)可得

故(9)式成立.

例4在△ABC中，设n为正整数，求证：

(10)

证明由不等式xn+yn+zn≥

例5在△ABC中，求证：

(11)

证明

同理可得

由以上三式和例3中的不等式(9)可得

故(11)式成立.

注1以上各例中得到的不等式均为新的不等式，当且仅当△ABC为等边三角形时各式中等号成立.

注2《数学通报》2012年2月号问题2045为[5]：在锐角△ABC中，试证明

(12)

对于锐角△ABC，易见(11)式是(12)式的加强. (12)式仅是对锐角三角形的一个结论，而(11)式对于任意三角形均成立，因此本文例5是数学问题2045的拓广.