例谈伸缩变换在高中数学教学中的应用

张伟志

(山东省邹城市第二中学 273500)

伸缩变换是高等几何的重要组成部分，了解伸缩变换的性质会使一些高中数学中较难问题变得更为直观快捷.下面先来看一个例子.

解法研究

分析和略解:

令A(acosα,bsinα),B(acosβ,bsinβ)，

则C(-a(cosα+cosβ),-b(sinα+sinβ)).

由点C在椭圆上, 代入得

(cosα+cosβ)2+(sinα+sinβ)2=1

另一方面

其实，我们可以通过图形的伸缩变换快速得出结论.

对椭圆进行下面的伸缩变换

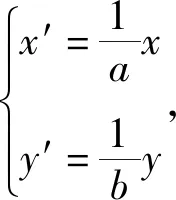
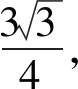
本质揭示

(1)理论依据

根据初等几何的知识，我们不难得出平面图形伸缩变换的以下性质：

①点经过变换后仍然是点，直线经过变换后仍然是直线，若一个点在直线上，变换后的对应点也在对应直线上；

②两条平行直线经变换后仍然平行，两条相交直线经变换后仍然相交，共点的直线经变换后仍为共点直线；

③两条平行直线段长度之比在伸缩前后不变，我们不妨称为伸缩不变量；

④两封闭图形的面积比是伸缩不变量.

由上述的不变量经过“组合”，可导出许多伸缩不变量，如线段的中点、三角形的中线和重心、平行四边形的相关性质等，特别要注意的是，角度不是伸缩不变量.

(2)引例剖析

引申和推广

(1)伸缩变换在面积问题中的应用

虽然角度不是伸缩不变量，在单位圆中的直角三角形经伸缩变换后不一定为直角三角形，但是我们可以依据伸缩变换的性质，得出变换前后的图形面积之间的数量关系.

(2)伸缩变换在点线关系中的应用

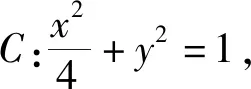
下面我们运用伸缩变换的思想对上述命题加以验证，首先我们来验证该命题在⊙O：x2+y2=a2(a>0)中为真命题.

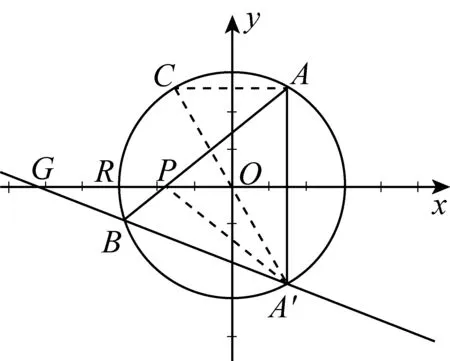
证明：连接A′O并延长，延长线交⊙O于点C,连接AC与A′P，设直线A′B与x轴的交点为G，并设R为⊙O与x轴的一个交点，如图所示.

则AC与x轴平行，所以∠CAB=∠OPA,

由点A与点A′关于x轴对称,

得∠OPA=∠OPA′,又由∠OA′G=∠CAB,

可得∠OA′G=∠OPA′,

所以△OPA′∽△OA′G,

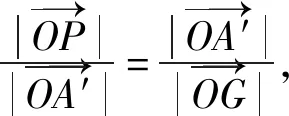
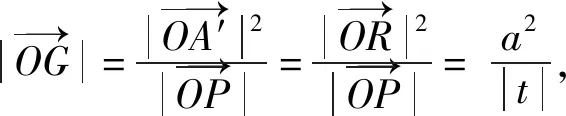
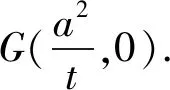
圆是平面图形中最优美的图形，当椭圆通过伸缩变换为相对应的圆时，椭圆中许多较为复杂的点线关系问题便会迎刃而解了.

(3)伸缩变换在最值问题中的应用

(1)求椭圆E的方程；

(2)设过点A的动直线l与椭圆E相交于P、Q两点，当△OPQ的面积最大时，求直线l的方程.

可得x′2+y′2=4，变换后的图象如下图所示.

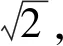
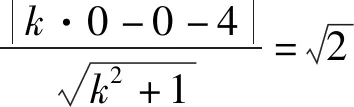
可见，利用伸缩变换将椭圆转化成圆，再通过讨论直线与圆的位置关系，可使问题得以简化，这种变换在圆锥曲线最值问题中应用较为广泛.

分析和略解：

可得x′2+y′2=1，为了方便观察，我们作了变换后的图象如下图所示.

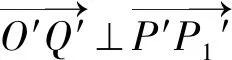
四边形OPNQ与四边形ONQP1在变换前后均为平行四边形，

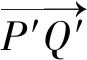
同理可得

当且仅当m=n时等号成立，

抛物线与双曲线的变换不及椭圆那么完美，但恰到好处地转化应用仍然可以使问题变得直观简洁，在不超越伸缩变换性质的范畴内，各类特殊的变换均可以作为解题的利器．以上仅是笔者对这类试题的一些肤浅的思考，更多方法还有待于我们在实践中不断加以探索与总结．