形之完美表达 数之完美表现——对诱导公式教学的深入思考和分析

黄邵华 何 娇

(1.广西南宁市第二中学 530022；2.北京师范大学附属实验小学 100875)

在“三角函数的诱导公式”这节内容的教学设计准备过程中，在课堂的教学上以及课后的总结中，都会不断让我们产生思考：对于几何图形“圆”与代数恒等式“诱导公式”，一形一数，二者之间竟然有着如此美妙的联系，这种联系是巧合吗？是否具有一般性呢？笔者经过反思和推演，作出以下分析.

平面上存在一些呈中心对称的几何图形，该图形绕其对称中心旋转角度π后，依然与原图形重合，但是圆不仅具有此性质，甚至圆绕圆心旋转任意角度后仍与原图重合.另外，平面上存在一些呈轴对称的几何图形，该图形可能会有一条或者多条对称轴，但是圆不仅具有此性质，甚至过圆心的任意直线为都可以成为圆的对称轴.因为上述旋转和对称的任意性，使得“圆”能够成为自然界中最完美的图形之一.

几何性质上的表现，必然能在代数上进行表达.接下来，我们以单位圆为代表，分别从圆的一般方程和参数方程的角度出发，证明圆的两个完美的几何性质，并从两种证明过程中探究圆的几何性质在代数形式上的表达.

1 绕点旋转的任意性

求证：圆绕圆心旋转任意角度后仍与原图重合(后简称“绕点旋转的任意性”).

在不影响结论的一般性前提下，为了方便证明，我们不妨设该圆为圆心在坐标原点的单位圆(后同).

方法一：设P(x,y)为圆O上任意一点，设其绕着圆心旋转角度θ(θ∈R)后，对应点为P′(x′,y′).

中华民族优秀传统文化是“两治”现代化的内生动力。习近平指出：“我国今天的国家治理体系，是在我国历史传承、文化传统、经济社会发展的基础上长期发展、渐进改进、内生性演化的结果。”[9]“两治”现代化，空想不行、闭门造车不行，要善于学习，向老祖宗学习、向国外学习，遵循高等教育发展规律，借助传统的深度挖掘和新时代的重新阐释，总结借鉴国外知名高校的办学理念、办学模式、管理方法，海纳百川、兼容并蓄，创造性内化、创新性发展，在人类命运共同体中讲好中国故事。

根据坐标旋转变换公式可得

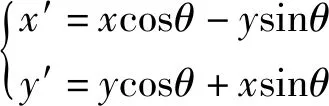
(1)

因为

x′2+y′2=(xcosθ-ysinθ)2+(ycosθ+xsinθ)2

=x2+y2=1,

所以，圆上任意一点绕着圆心旋转任意角度后仍然在该圆上，即其旋转任意角度后，与原图重合.

方法二：结合圆O的参数方程，设圆O上任意一点P的坐标(x,y)为

(2)

则该点绕圆心O旋转角度θ后得到的点P′(x′,y′)满足

(3)

显然点P′依然圆O上.

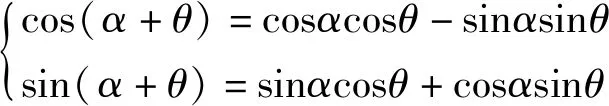
(4)

上述(4)式正是正余弦函数的两角和公式.

因此，我们可以认为正余弦函数的两角和公式正是圆的几何性质：圆绕圆心旋转任意角度后与原图重合，在代数形式上的表达；反之，圆绕圆心旋转任意角度后与原图重合，也即为正余弦函数两角和公式的几何意义.

2 绕轴对称的任意性

求证：圆关于任意一条过圆心的直线对称(后简称“绕轴对称的任意性”).

方法一：设P(x,y)为圆O上任意一点，设其关于直线y=kx(k≠0)的对称点为P′(x′,y′).

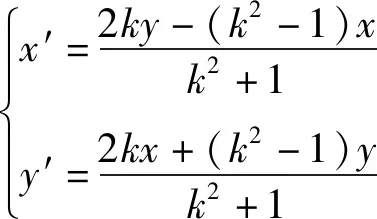
(5)

又因为

因此P′点依然在该圆上.

若k=0或k不存在，易证得P′点依然在该圆上.

因此，证得圆上任意点关于任意过圆心的直线的对称点依然在该圆上，所以圆具有“绕轴对称的任意性”.

方法二：若采用圆的参数方程，设P(cosα,sinα)为圆O上任意一点，过圆心的直线倾斜角为θ.设P关于该直线的对称点为P′(x′,y′)，若设P′所在终边所对应角为α′，则有α+α′=2θ，即α′=2θ-α，所以有

(6)

显然可得点P′也在圆O上.

上述两种方法分别通过圆的一般方程和参数方程证得圆“绕轴对称的任意性”.结合两种方法的证明过程，有如下推导:

化简后得

(7)

由(4)我们可以得到

代入(7)即有

(8)

而(8)式正是正余弦函数的两角差公式.

因此，我们可以认为正余弦函数的两角差公式正是圆的几何性质：圆关于任意一条过圆心的直线对称，在代数形式上的表达；反之，圆关于任意一条过圆心的直线对称，也即为正余弦函数两角差公式的几何意义.

3 两类任意性的特殊情形

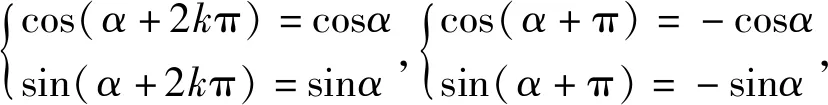
而这三组公式，恰为高中数学教材中的诱导公式(一)、(二)和(六)，显然，这三组诱导公式为正余弦函数的两角和公式的特殊情形.

除此之外，通过前面正余弦函数的两角和公式的几何意义，我们可以认为：

而这三组公式，恰为高中数学教材中的诱导公式(三)、(四)和(五)，显然，这三组诱导公式为正余弦函数的两角差公式的特殊情形.

除此之外，通过前面正余弦函数的两角差公式的几何意义，我们可以认为：

诱导公式(三)、(四)和(五)即为圆的几何性质：圆心在原点的圆关于x轴、y轴、直线y=x对称，在代数上的表达；反之，圆心在原点的圆关于x轴、y轴、直线y=x对称，即为这三组诱导公式的几何意义.

4 小结

“数与形，本是相倚依，焉能分作两边飞？数缺形时少直观，形少数时难入微.”著名数学家华罗庚先生的这几句话，很好地阐述“数”与“形”的相互关系及其结合思考数学问题的重要性.

圆作为一个堪称完美的图形，它的几何性质在代数上的表现，如果用圆的普通方程来刻画，不仅描述过程繁琐，而且直观性不强.但我们引入圆的参数方程后，将圆上点的坐标用三角函数来表示，则能非常明显而直观地发现圆的一些特殊性质.

将两种方程结合起来思考的推演后，我们可以得到：

正余弦函数的两角和差公式为圆绕点旋转和绕轴对称的任意性在“数”上的表达；

圆绕点旋转和绕轴对称的任意性为正余弦函数的两角和差公式在“形”上的表现；

诱导公式为圆绕点旋转和绕轴对称的特殊性在“数”上的表达；

圆绕点旋转和绕轴对称的特殊性为诱导公式在“形”上的表现.