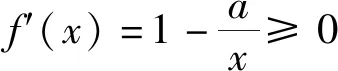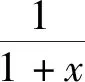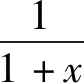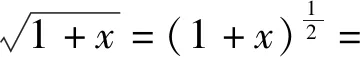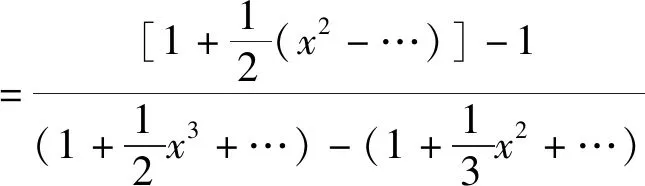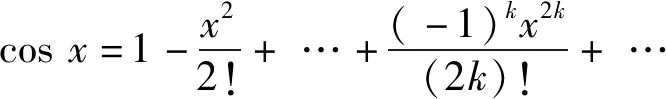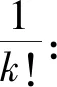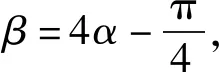大学视角下的中学数学(泰勒展开)(续)

李尚志

(北京航空航天大学 100083)

4. 无名英雄

中学生不难了解和应用泰勒展开, 借助它想出解法, 算出答案. 虽不能将它写进答卷, 但可以让它作无名英雄, 用求导来实施它的计划.

Ⅰ. 什么是泰勒展开:如果函数f(x)在某点c附近可以展开成x-c的无穷级数

f(x)=a0+a1(x-c)+…+ak(x-c)k+…

(4′)

就称为f(x)在c的泰勒展开.

只要有了展开式(4′), 取x=c得f(c)=a0. 求导再取x=c得导数f′(c)=a1. 求导k次再取x=c得k阶导数f(k)(c)=(k!)ak.

(4)

例如, ex的导数(ex)′=ex等于自身, 任意阶导数(ex)(k)=ex等于自身. 在x=0 的值和所有各阶导数都是1, 代入(4′) 就得到展开式

(5)

要使泰勒展开式(4) 右边的无穷级数真正等于左边的函数, 还须将x的取值限制在一定范围内, 才能够保证无穷级数的极限存在. 例如,对数函数ln(1+x) 的展开式要求-1

Ⅱ. 两项用途

(1) 判定f(c) 是否极值

在c附近足够小范围内,f(x)-f(c)=a1(x-c)+…=am(x-c)m+am+1(x-c)m+1+…的正负号与最低次非零项am(x-c)m≠0的正负号相同, 高次项忽略不计. 当m为奇数,f(c)不是极值. 当m是偶数,am<0 时f(c) 是极大值,am>0时f(c) 是极小值.

例3(2019北京市海淀区高三一摸) 已知函数f(x)=xln(x+1)-ax2. 当a<0时, 求证: 函数f(x) 存在极小值.

容易看出进一步的结论: 当a<1时f(0)是极小值,a>1是极大值,a=1时f(0) 不是极值.

中学生不能在答卷上作泰勒展开. 在草稿上用泰勒展开知道了f(0)是极小值. 在答卷上就可以计算f′(0)=0,f″(0)=1+1-2a>0来说明f(0) 是极小值.

以上例1, 例3都是给定了c判定f(c) 是否极值. 如果不知道c要求极值点, 需要先解方程f′(x)=0 求出c满足必要条件f′(c)=0, 再判定是否满足充分条件.

例4(2017理科数学全国卷Ⅲ第21题) 函数f(x)=x-1-alnx．

(1) 若f(x) ≥ 0，求a的值；

求m的最小值．

分析(1) 看出f(1)=0, 可根据f(1)=0 是最小值求a.

用泰勒展开摸脉: 令x=1+t得

要保证x=1 附近始终f(x) ≥ 0, 必须1-a=0,a=1, 此时

f(1)=0 是极小值, 在x=1 附近f(x) ≥ 0. 但ln(1+t) 仅在-11 时的变化情况. 还需通过lnx的导数判定它在定义域(0，+∞) 内的变化情况. 解法如下:

解由f(1)=0 知f(x) ≥ 0 当且仅当

f′(x) ≤ 0 (当0

(2) 出题人提示你利用第(1) 小题得到的不等式x-1-lnx≥ 0即lnx≤x-1 即ln(1+t) ≤t来解第(2) 题.

Pn

不过, 这个提示转弯太多, 在考场上恐怕难于从x-1-lnx≥ 0联想到ln(1+t) ≤t再联想到将第(2) 小题的乘积Pn两边取对数. 如果你熟悉前面给出的指数函数泰勒展开式(5):

马上就看出当x>0 时ex>1+x. 更容易联想到

至于为什么ex>1+x, 别说泰勒展开教的. 一切归功于导数: 由f(x)=ex-(1+x) 的导数f′(x)=ex-1 的正负证明f(0)=0 是最小值,ex>1+x就对所有x≠0 成立.

如果g(c)≠0, 直接将x=c代入得极限

设g(c)=0, 将f(x)，g(x) 在c泰勒展开, 得

其中am≠0,bk≠0 分别是分子分母的最低次非零项系数, 更低次项系数ai=0=bj(∀0 ≤i

如果m

此时极限λ不存在.

中学生先掌握求极值和求极限这两个用途, 是因为这两条只须关注函数在某点c附近的状况, 可以忽略高次项, 将函数直接化成单项式am(x-c)m来处理, 特别快捷.

Ⅲ. 记住泰勒展开式

先背熟本文前面反复用到的

(6)

如果展开式(6) 背起来有困难, 将它左右两边求导, 得到等式

(7)

怎么背(7)? 它的右边就是等比数列和

当n→∞ 的极限. 当|x|<1 时, (-x)n→0, 得到的就是(7).

展开式(7) 可以用来检验ln(1+x)的展开式是否正确. 还可以对(7) 求导(再乘-1) 得到新的展开式

(8)

(7),(8) 是幂函数(1+x)-1，(1+x)-2展开式. 任意幂函数展开为

(1+x)m=1+mx+…

(9)

【启示】只锈坏了一个扣，整条铁链也就失去了他的价值。不要对缺点和错误报以宽容的态度，哪怕是一丁点儿。否则，他就会像草原上的火种，一发不可收拾。

例6求sinx，cosx在x=0 的泰勒展开式.

解记f(x)=sinx, 则f′(x)=cosx.

f″(x)=-sinx.f(2k)(x) =(-1)ksinx.

f(2k+1)(x)=(-1)kcosx.f(2k)(0)=0,

代入

(10)

(11)

在ex的泰勒展开式中将x换成ix, 得到

=cosx+i sinx

(cosx+i sinx)n=(eix)n=einx

=cosnx+i sinnx

sinx，cosx的展开式不用背. 在eix的展开式中取实部得cosx, 取虚部得sinx.

Ⅳ. 计算e 和π

我们会算加减乘除, 却很难计算其它函数值, 如指数, 对数, 三角函数等. 用泰勒展开将它们展开成幂级数, 变成加减乘除, 都能算出来了.

自然对数的底e由基本极限

定义, 却很难由基本极限算出来. 比如取n=10000将1万个1.0001相乘, 费了很多功夫, 得到近似值2.71815 与准确值2.71828 …相比,只有前四位数字正确.

不过可以用牛顿二项式定理来算

令n→∞ 取极限得到

(12)

比计算e更引起兴趣的是计算π. 我从小学学了加减乘除形成的理念就是什么都可以自己算.小学高年级学了圆周率, 第一次遇到自己不能算的. 就对怎样算π感兴趣. 最开始是用尺子量水杯的周长和直径来相除, 由于精确度不够, 无法得出3.14. 后来看见有的书上说祖冲之用正多边形周长来逼近圆周长. 我也按照这个方法, 从正六边形周长开始, 利用勾股定理依次计算正12边形, 24边形的边长. 每次都要开平方. 越算越繁. 还没得到3.14 就算不下去了. 很怀疑祖冲之怎么可能用这个方法算到小数点后面7位.

越学到后来, 自己不能算的东西越多. 三角函数不能算, 除了特殊角0°，30°，45°，60°，90°, 其余角度的三角函数都不能算. 后来学了对数,也不能算. 每个学生发一本四位数学用表. 不会算就查表. 我去问老师:正弦表怎么算出来的？老师说: 别管它怎么编出来的, 只要学会查表就行了. 我心里想: 我可以查表. 编表的人怎么办呢？他查上一个表. 编上一个表的人查更上一个表. 一直查下去, 总得有第一个人编出第一份表让以后的人查. 第一个人怎么算出来的? 我不能再去问老师. 这个问题就一直存在心里. 终于有一天, 在某一份数学用表最后半页纸上看见一些公式. 其中包括

我突然明白了: 这就是算正弦表的公式. 将每个角用弧度数x表示, 代入上式右边, 只需要做加减乘除就能算出正弦来. 这就本文例5算出的正弦函数的泰勒展开式. 不过我当时并不知道它叫泰勒展开, 只知道它可以将正弦变成加减乘除来计算. 还有算余弦, 正切的公式, 算对数, 反对数的公式. 反对数就是已知对数求真数, 就是指数函数.

终于有一天, 在书店的一本小册上看到了利用反正切函数泰勒展开计算π的方法. 反正切函数泰勒展开式如下:

(13)

粗看起来与正弦的展开式差不多, 都只有奇次项没有偶次项. (这是因为sinx，arctanx都是奇函数.) 正负号也是交替出现. 每一项x2k+1的系数也都有分母2k+1. 所不同的是sinx的分母是阶乘(2k+1)!,求导之后约掉奇数2k+1, 剩下偶数的阶级乘(2k)!, 变成cosx的展开式. 反正切arctanx展开式2k+1 次项的分母2k+1 没有阶乘, 求导约掉了就没有分母了, 系数变成1:

将x=1代入展开式(13) 得

有个几何题, 证明正方形拼成的如下图形中∠1+∠2+∠3=90°.

图1

题目不难, 只要证明以∠1 为外角的两个三角形相似就行了. 不难发现

所证明的就是

(14)

(15)

等式(15) 叫做马青公式. 我在读高中的时候在一本小册子上见到利用马青公式和泰勒展开式算π的方法, 就照章办事, 花了半小时笔算就得出了π=3.14159265, 比祖冲之的精确度还高一位.